基于特征变量与支持向量机回归克里格(SVRK)法的湿地土壤有机质空间变异特征分析①
陈思明,王 宁,秦艳芳,张红月
基于特征变量与支持向量机回归克里格(SVRK)法的湿地土壤有机质空间变异特征分析①
陈思明1,2,王 宁2,秦艳芳1,张红月1
(1 闽江学院海洋学院,福州 350108;2 福建农林大学林学院,福州 350002)
选取有效变量与适宜方法有助于揭示河口湿地土壤有机质的空间分异特征,对维护湿地生态平衡和全球碳循环具有重要作用。以福州市闽江河口湿地为研究区,采用逐步回归分析(SLR)与主成分分析(PCA)法筛选显著的特征变量,运用支持向量机回归克里格(SVRK)法分析了湿地土壤有机质的空间异质性,并与神经网络克里格(BPNNK)法、回归克里格(RK)法进行了比较。结果表明:通过SLR和PCA分析发现,归一化植被指数(NDVI)、比值植被指数(RVI)、土壤水分指数(PDI)、汇流累积量(FA)及沉积物移动指数(STI)与土壤有机质含量关系密切,其判定系数2为0.446,显著性概率值<0.000 1,可转换为3个独立的特征变量用于模型的预测。研究区土壤有机质的空间变异主要受结构性因素影响,呈现出“北低南高”的空间格局,采用SVRK模型的预测精度更高,能较好地体现河口湿地土壤有机质的空间异质特征。该研究可为同类区域的土壤有机质空间特征研究提供方法支撑。
河口湿地;土壤有机质;逐步回归分析法;支持向量机回归克里格法
河口湿地位于陆地与海洋生态系统的交错地带,是深入研究湿地各种生态要素相互作用的重要区域,在生物多样性、区域生态平衡、全球生物化学循环中发挥着关键的作用[1]。然而,河口湿地又是一个较为独特的生态区,其土壤常年受到地表径流、泥沙输移、冲淤演变、周期性潮汐等多重作用影响[2],导致土壤属性在空间分布上呈现出明显的异质性[3]。土壤有机质(soil organic matter, SOM)作为土壤属性的重要组成部分,可促进植物生长发育,改善土壤理化性质,对湿地生态系统和全球碳氮循环影响显著[4-5]。因此,精准地掌握土壤有机质空间变异规律,对河口湿地生态与环境的可持续发展具有重要意义。
受河口湿地特殊环境影响,单纯依靠人工野外调查难以全面、精准地获取土壤属性空间信息[6],如何在有限的采样点基础上,选取最适宜的空间预测方法尤为重要。目前,普通克里格(OK)法、简单克里格法等地统计学方法能够从SOM的空间自相关特征出发[7],并对预测误差做出理论估计,已被广泛运用。但是地统计学法仅是依靠于样本数据的空间自相关性,未能考虑到各种成土因素和生态过程的影响,在复杂环境下其预测精度会受到较大限制[8]。对此,部分学者采用多元线性回归法、BP神经网络法、随机森林法等线性或非线性算法[9-10]来预测SOM的空间分布,进而分析其空间异质特征。这类算法可利用环境因素与土壤有机质间映射关系,获取较为精准的预测结果[11],但是也存在一定局限性,其未能较好考虑到残差的空间自相关影响[12]。近年来,国内外部分学者[13]将线性或非线性算法与地统计学法相结合,构建混合地统计学模型并运用于土壤属性空间预测。该方法能同时利用土壤属性的空间自相关性以及与环境因子间的异相关性,可更为真实地反映复杂环境下土壤属性的变异情况[14]。通过文献集成分析发现,以往的研究在建模方法上多采用回归克里格(RK)法与神经网络克里格(NNK)法。RK法通常是基于最小二乘线性回归(OLS)的空间插值方法,该方法未能较好地描述土壤属性与环境变量间的非线性关系,容易出现过拟合现象[15]。NNK法是将神经网络模型与OK法相结合,能较好地表达土壤属性与多源环境变量间的非线性映射关系[16]。但是神经网络模型对训练样本的要求较高,测试过程较为复杂,需不断调整模型参数以获取更高的预测精度[17]。另外,合理的变量类型与个数有利于简化模型结构,减少弱相关因子的干扰,进而提高模型的预测精度,已成为土壤属性空间预测的关键步骤[18]。然而,80% 以上的研究是通过相关性分析或主成分分析(PCA)法来建立环境变量与土壤属性间的关系[19],未能较好地体现不同环境变量在模型预测过程中的贡献度[20]。因此,如何进一步发挥混合地统计学模型在土壤属性空间预测中的优势,提高模型的运行效率和泛化能力,需对模型的适用性和辅助变量的有效性问题进行深入探讨。
支持向量机回归(SVR)算法是一种在高维特征空间中构建线性决策函数的新型学习方法。该算法的泛化能力较好,能解决高维数据问题,避免神经网络出现的局部最优解[21]。支持向量机回归克里格法(SVRK)是SVR模型的一种拓展,其借助地统计学法来分析残差的空间自相关对模型拟合的影响,实现对观测对象的连续性预测和局部变异预测。逐步回归分析(SLR)法是将一组变量逐个引入模型,并对已经选入的解释变量进行检验,以确保每次引入新的变量之前回归方程中只包含显著性变量。对此,本研究利用SLR法和PCA法来筛选主控环境因子,提取独立的特征变量,结合SVR算法与OK法构建混合地统计学模型,并与RK法、BPNNK法进行对比,深入探索模型的适用性,以期为同类区域的SOM空间异质性研究提供方法支撑。
1 材料与方法
1.1 研究区概况
研究区位于福建省福州市闽江入海口处的鳝鱼滩湿地,是闽江河口区面积最大的天然潮滩湿地(图1),地理坐标为26°00′ 36″ ~ 26°03′12″ N,119°36′30″~ 119°40′40″ E,总面积约为3 120 hm2。该区地处中亚热带与南亚热带的过渡地带,气候暖热潮湿,年均气温为19.3℃,年均降雨量为1 380 mm。潮汐为正规半日潮,潮水涨落频繁。土壤类型以滨海盐土为主,pH呈偏酸性到中性。植被主要包括互花米草()、芦苇()、短叶茳芏()和扁穗莎草()等。
1.2 野外采样与环境变量获取
考虑到湿地的自然景观保护和样点分布的均匀性,先在室内利用Google Earth高分辨遥感影像对采样点进行初步布设。2017年8月2—12日在研究区手持GPS进行定点,以定点为中心设置10 m × 10 m小样方,按照“五点混合采样法”采集土壤样品,采样深度为0 ~ 30 cm,共采集土壤样品105个(裸滩区样品70个,互花米草区样品16个,其他植被区样品19个),并记录各采样点的坐标(图1)。将采集的土壤样品带回实验室,经过自然风干和研磨过筛,采用重铬酸钾氧化-外加热法测定SOM含量。
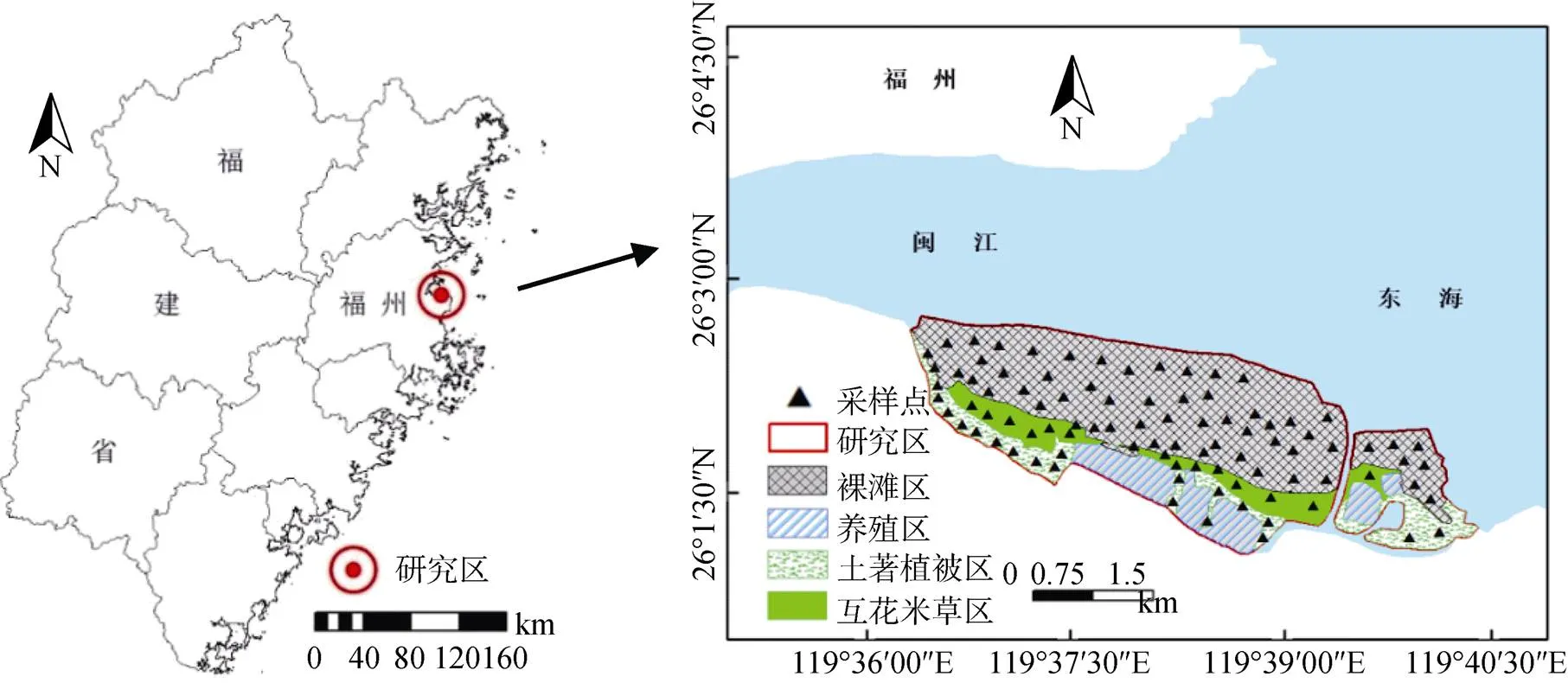
图1 研究区位置及采样点分布图
根据研究区的实际情况和相关文献,利用2017年8月8日的Landsat8 OLI影像(行列号118/42,云量7.58)和数字高程模型DEM(空间分辨率30 m),通过ENVI5.1软件的波段运算和ArcGIS10.2软件的水文分析模块、空间插值模块、栅格计算器等,提取植被、土壤、水文和地形等多个环境因素,具体环境变量见表1。遥感影像数据和数字高程模型来源于地理空间数据云(http://www.gscloud.cn/)。

表1 基于Landsat OLI和DEM生成的环境变量
1.3 特征变量的提取方法
本研究采用SLR法和PCA法提取特征变量。先采用SLR模型对所有环境变量进行判定,通过F检验和T检验不断剔除弱相关变量,直至选出的解释变量集最优,再运用PCA法对选取的变量集进行降维,提取特征值大于1或方差贡献度达到85% 以上的主成分,作为特征变量用于SOM含量的空间建模。SLR、PCA法主要采用SPSS 22.0软件来实现。
1.4 模型的构建与验证
利用SVR算法与OK法相结合,生成的一种空间插值方法(SVRK)。该方法是通过SVR模型建立SOM与环境变量之间非线性映射关系,再利用OK法对残差项进行空间插值,以获取最终预测结果,其过程可表示为:
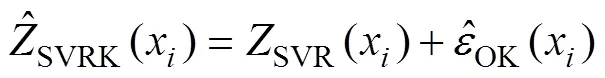
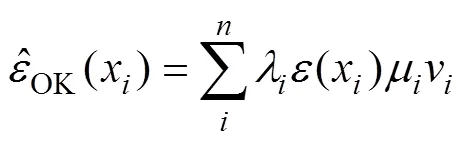
式中:(x)为SVR模型拟合的残差项,λ为邻域观测值对点观察值的贡献权重,可通过变异函数进行确定,其表达式为:
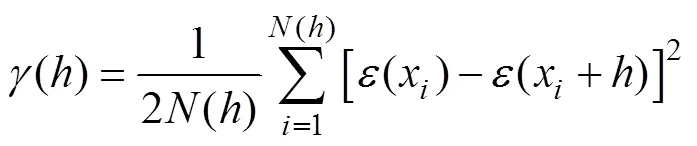
式中:()为变异函数,(x)、(x+)分别表示在x和x+空间位置处的残差值,表示采样点的对数。
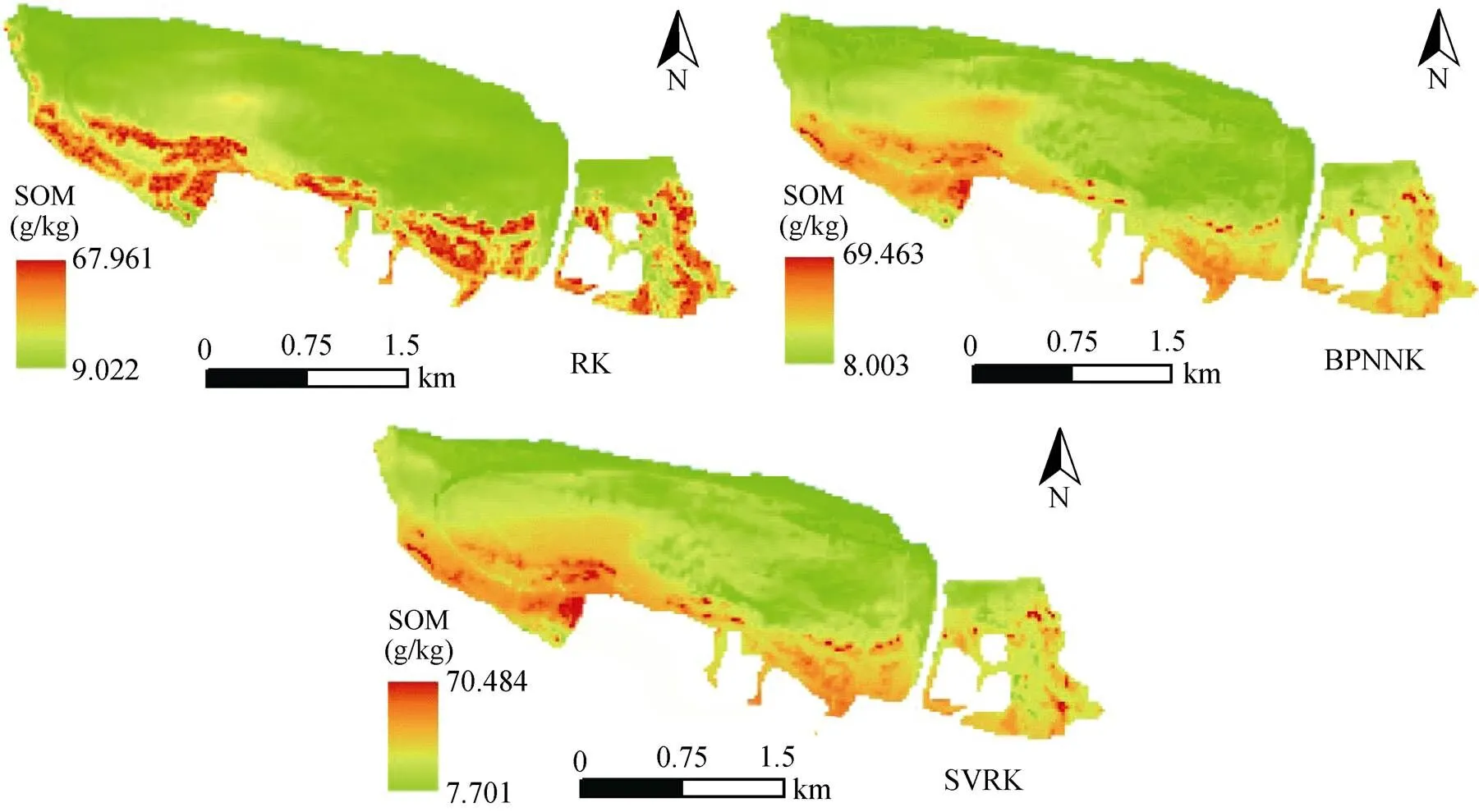
为了验证模型的预测效果,将SVRK法与BPNNK法、RK法进行对比,并采用判定系数(2)、均方根误差(RMSE)和相对分析误差(RPD)进行衡量。其中,2和RMSE是评价模型预测精度的指标,2越大,RMSE越小,模型预测精度越高。RPD是描述模型预测能力的直观指标,RPD>2时,说明模型的预测能力极佳;1.4 由表2可以看出,研究区105个采样点的SOM含量最小值为7.496 g/kg,最大值为70.948 g/kg,平均值为28.563 g/kg,标准差为14.422 g/kg。通过变异系数分析发现,SOM含量的变异系数为50.49%,属于中等程度变异。不同环境因子的变异系数则差异较大,其中平面曲率(Ct)和剖面曲率(Cp)的变异系数较大,分别为139.02% 和143.84%,属于强变异;而地表粗糙度(SR)的变异系数则较小,属于弱变异。采用Kennard-Stone算法将105个SOM样本集划分为80个训练集和25个测试集,并进行正态分布检验,结果显示训练集、测试集符合正态分布。 表2 研究区土壤有机质及环境因子的描述性统计特征 注:表中各环境变量含义见表1。 由表3可知,通过SLR模型对所有变量进行判定,筛选出5种变量组合。其中,第5种变量组合的判定系数2为0.446,显著性概率值<0.000 1,为SOM含量空间分布预测的最佳变量组合,因此本研究选取第5种变量组合进行PCA分析。 由表4可知,通过PCA分析将5个变量转换为3个主成分,其中,第1主成分在NDVI、RVI、PDI上具有较高的因子载荷,贡献率为54.17%,主要反映遥感影像信息;第2、3主成分在FA和STI上具有较高的载荷值,主要体现径流变化和沉积物运移信息。这3个主成分累计可解释总方差的94.12%,保留原有变量的大部分信息,可作特征变量进行SOM的空间建模。 表3 土壤有机质与环境因子的逐步回归分析 表4 环境变量的PCA分析 2.3.1 SVR、BPNN和OLS模型预测 利用3个主成分(PC1、PC2、PC3)为自变量,SOM含量为因变量,分别采用OLS、BPNN和SVR模型对SOM含量空间分布进行预测。由表5可知,SVR模型的预测精度最高,其训练集与测试集的2分别为0.619、0.593,比BPNN模型提高0.088和0.051,比OLS模型提高0.19和0.151,对应的RMSE则最小。从模型的预测能力上看,SVR模型的RPD值(1.601)较高,模型能够对SOM含量进行预测,而OLS模型的RPD为1.366,模型则不能对SOM含量进行预测。由此表明,SVR模型能够保持数据稳健性,提高预测效果。 表5 OLS、BPNN和SVM模型的预测精度对比 2.3.2 地统计学分析 由表6可知,SOM含量、OLS残差、BPNN残差及SVR残差分别适合高斯模型与指数模型,模型拟合效果较好。块金效应表示系统变量的空间自相关性[26],块金效应<25%,系统变量的空间自相关性较强,受结构性因素影响;25%≤块金效应≤75%,系统变量的空间自相关性中等,受结构因素和随机因素影响;块金效应>75%,系统变量的空间自相关性较弱,受随机因素影响。研究区SOM和3个残差的块金效应分别为38.88%、27.00%、25.98% 和36.27%,呈现出中等程度的空间变异,受结构性因素影响较大。变程是描述空间范围内达到基台值时对应的步长,超出此范围空间相关性不存在。3个残差的空间自相关范围与SOM较为接近,基本保留原有的空间结构特征。 表6 土壤有机质与拟合残差值的半方差参数 2.3.3 SOM的空间分布特征 根据上述分析结果,分别对OLS残差、BPNN残差和SVR残差进行OK插值,得到RK、BPNNK和SVRK模型预测的土壤有机质空间分布图(图2)。由图2可知,研究区SOM含量在空间分布上呈现出“北低南高”的变化趋势,具有明显的空间异质性,这与研究区的植被覆盖、土壤属性、地形特征等环境因子的空间变化情况较为吻合。从预测效果上看,RK模型能体现研究区SOM的空间分布特征,但是未能较好地描述局部信息,具有一定的平滑效应;BPNNK与SVRK模型的预测效果较好,能体现土壤有机质含量高低值间的变化情况,凸显斑块化现象。但SVRK模型的预测效果更佳,其预测值在在7.701 ~ 70.484 g/kg,与实际情况最为接近。 图2 研究区SOM的空间分布图 为了进一步验证SVRK模型的预测效果,利用25个测试集绘制1∶1关系图(图3)。通过图3可知,SVRK模型的样本点基本分布在1∶1关系线两侧,模型拟合程度极佳。与RK、BPNNK模型相比,SVRK模型的2和RPD分别提高了0.163、0.058和0.394、0.172,RMSE则分别减低了1.794、0.683,说明该SVRK模型可有效提高河口湿地土壤有机质含量的预测精度。 图3 RK、BPNNK 和SVRK模型精度验证 SOM的空间分布受到植被、土壤、水文、地形等诸多因素的影响,呈现出明显的空间异质性。要精准地预测SOM空间分布,揭示其空间异质特征,应充分考虑不同环境因子对SOM的响应程度[8]。本研究根据闽江河口湿地的实际情况,选取光谱、植被、地形和水文等23个环境因子,通过SLR与PCA法来分析不同环境因子对SOM含量的敏感性。结果表明,SOM含量的空间分布与NDVI、DVI、SPI、AS和STI关系密切,显著性概率值<0.000 1,可转换成3个独立的特征变量参与模型预测。该研究结果与徐夕博等[27]和Abuduwaili等[28]的研究结果较为一致的,但在方法上存在一定的差异。如,徐夕博等[27]是采用PCA法来探讨环境变量与SOM含量关系,进而选取特征变量。PCA法作为一种变量的降维方法,其未能较好去除弱相关变量的干扰,探寻最优变量组合。而本研究联合采用SLR与PCA法分别从因子筛选和因子降维的角度出发,能更为有效探寻影响SOM空间分布的主控因子。 对比RK、BPNNK和SVRK模型的预测效果发现,SVRK模型可显著提高SOM含量的预测精度,揭示复杂湿地环境下SOM空间异质特征。这可以归因于3点:首先,SVR通过二次规划方法分析多源辅助变量与SOM含量的非线性关系,得到全局最优解,克服BPNN法容易陷入局部最小解的缺点。Song等[29]对比SVRK、BPNNK和RK模型预测SOM空间分布的效果,结果表明SVRK模型具有更高的决定系数和预测性能,这与本研究结果较为一致。其次,SVR模型能够较好地捕捉SOM含量随着植被、土壤、水文等微环境变化而变化的细节信息,实现全局性预测与特定点预测。曾胤等[30]研究也表明,SVR模型能较好反映样本的“纯信息”变化,可有效提高模型的预测精度。最后,SOM含量空间分布受到结构因素和随机性因素的影响,利用Kriging法对残差进行空间插值,综合考虑结构性部分和随机性部分的模拟,可提高SOM空间分布的预测精度。但是本研究在模拟过程中,在土壤类型、人为活动、潮汐作用等因素上未能全部涉及,不可避免产生一定误差,今后研究需要进一步引入更多辅助变量,以更为精准揭示河口湿地SOM空间异质特征。 1)通过SLR法检验发现,NDVI、DVI、SPI、AS和STI与SOM含量关系密切,其判定系数2为0.446,显著性概率值<0.000 1。 2)运用主成分变换法将5个变量转换成3个独立的特征变量,保留原有变量的大部分信息,可作为特征变量用于SOM的空间建模。 3)研究区SOM空间变异主要受结构性因素影响,呈现出“北低南高”的空间格局,对比RK、BPNNK模型,SVRK模型的预测结果与实际情况更为吻合,突出SOM空间分布的细节信息。 [1] Negrin V L, Spetter C V, Asteasuain R O, et al. Influence of flooding and vegetation on carbon, nitrogen, and phosphorus dynamics in the pore water of a Spartina alterniflora salt marsh[J]. Journal of Environmental Sciences, 2011, 23(2):212–221. [2] Huang X, Wang X P, Li X Z, et al. Distribution pattern and influencing factors for soil organic carbon (SOC) in mangrove communities at Dongzhaigang, China[J]. Journal of Coastal Research, 2018, 342: 434–442. [3] 张枝枝, 张福平. 渭河两岸缓冲带的土壤有机质含量分布特征及其影响因子[J]. 土壤, 2017, 49(2): 393-399. [4] 王琪, 吴成永, 陈克龙, 等. 基于多光谱遥感图像的青海湖流域土壤有机质估算初探[J]. 土壤, 2019, 51(1): 160-167. [5] Osland M J, Gabler C A, Grace J B, et al. Climate and plant controls on soil organic matter in coastal wetlands[J]. Global Change Biology, 2018, 24(11): 5361–5379. [6] 陈思明, 邹双全, 毛艳玲, 等. 土壤光谱重建的湿地土壤有机质含量多光谱反演[J]. 光谱学与光谱分析, 2018, 38(3): 912-917. [7] 杜佩颖, 张海涛, 郭龙, 等. 平原丘陵过渡区土壤有机质空间变异及其影响因素[J]. 土壤学报, 2018, 55(5): 1286–1295. [8] 李启权, 王昌全, 岳天祥, 等. 基于神经网络模型的中国表层土壤有机质空间分布模拟方法[J]. 地球科学进展, 2012, 27(2): 175-184. [9] 于雷, 洪永胜, 耿雷, 等. 基于偏最小二乘回归的土壤有机质含量高光谱估算[J]. 农业工程学报, 2015, 31(14): 103–109. [10] Wang X P, Zhang F, Kung H T, et al. New methods for improving the remote sensing estimation of soil organic matter content (SOMC) in the Ebinur Lake Wetland National Nature Reserve (ELWNNR) in northwest China[J]. Remote Sensing of Environment, 2018, 218: 104–118. [11] Fernandes M M H, Coelho A P, Fernandes C, et al. Estimation of soil organic matter content by modeling with artificial neural networks[J]. Geoderma, 2019, 350: 46–51. [12] 孙钰森, 王维芳, 李国春. 基于地理加权回归克里格模型的帽儿山地区森林碳储量空间分布[J]. 应用生态学报, 2019, 30(5): 1642–1650. [13] Dai F Q, Zhou Q G, Lv Z, et al. Spatial prediction of soil organic matter content integrating artificial neural network and ordinary kriging in Tibetan Plateau[J]. Ecological Indicators, 2014, 45:184–194. [14] Dinh Q T, Liang D L, Thi Anh Thu T, et al. Spatial prediction of saline and sodic soils in rice-shrimp farming land by using integrated artificial neural network/regression model and kriging[J]. Archives of Agronomy and Soil Science, 2018, 64(3): 371–383. [15] 栾福明, 张小雷, 熊黑钢, 等. 基于不同模型的土壤有机质含量高光谱反演比较分析[J]. 光谱学与光谱分析, 2013, 33(1): 196-200. [16] 李启权, 王昌全, 张文江, 等. 基于神经网络模型和地统计学方法的土壤养分空间分布预测[J]. 应用生态学报, 2013, 24(2): 459–466. [17] 李静, 徐路路. 基于机器学习算法的研究热点趋势预测模型对比与分析——BP神经网络、支持向量机与LSTM模型[J]. 现代情报, 2019, 39(4): 23-33. [18] 王飞, 杨胜天, 丁建丽, 等. 环境敏感变量优选及机器学习算法预测绿洲土壤盐分[J]. 农业工程学报, 2018, 34(22): 102–110. [19] 江叶枫, 郭熙. 基于多源辅助数据和神经网络模型的稻田土壤砷空间分布预测[J]. 环境科学学报, 2019, 39(3): 928-938. [20] 陈运帷, 王文杰, 师华定, 等. 区域土壤重金属空间分布驱动因子影响力比较案例分析[J]. 环境科学研究, 2019, 32(7): 1213–1223. [21] Elbisy M S. Support Vector Machine and regression analysis to predict the field hydraulic conductivity of sandy soil[J]. KSCE Journal of Civil Engineering, 2015, 19(7): 2307–2316. [22] 杨顺华, 张海涛, 郭龙, 等. 基于回归和地理加权回归Kriging的土壤有机质空间插值[J]. 应用生态学报, 2015, 26(6): 1649-1656. [23] Mirzaee S, Ghorbani-Dashtaki S, Mohammadi J, et al. Spatial variability of soil organic matter using remote sensing data[J]. CATENA, 2016, 145:118–127. [24] 高中灵, 王建华, 郑小坡, 等. ADI土壤水分反演方法[J]. 光谱学与光谱析, 2016, 36(5): 1378-1381. [25] Razakamanarivo R H, Grinand C, Razafindrakoto M A, et al. Mapping organic carbon stocks in eucalyptus plantations of the central Highlands of Madagascar: A multiple regression approach[J]. Geoderma, 2011, 162(3/4): 335–346. [26] 方丽章, 李艳红, 李发东, 等. 艾比湖湿地土壤水分–盐分–养分空间异质性分析[J]. 农业环境科学学报, 2019, 38(1): 157-167. [27] 徐夕博, 吕建树, 吴泉源, 等. 基于PCA-MLR和PCA-BPN的莱州湾南岸滨海平原土壤有机质高光谱预测研究[J]. 光谱学与光谱分析, 2018, 38(8): 2556–2562. [28] Abuduwaili J, Tang Y, Abulimiti M, et al. Spatial distribution of soil moisture, salinity and organic matter in Manas River watershed, Xinjiang, China[J]. Journal of Arid Land, 2012, 4(4): 441–449. [29] Song Y Q, Yang L A, Li B, et al. Spatial prediction of soil organic matter using a hybrid geostatistical model of an extreme learning machine and ordinary kriging[J]. Sustainability, 2017, 9(5): 754. [30] 曾胤, 陆宇振, 杜昌文, 等. 应用红外光声光谱技术及支持向量机模型测定土壤有机质含量[J].土壤学报, 2014, 51(6): 1262-1269 Study on Spatial Variability of SOM in Estuary Wetland, Southeast China Based on Characteristic Variables and SVRK CHEN Siming1,2, WANG Ning2, QIN Yanfang1, ZHANG Hongyue1 (1 Ocean College, Minjiang University, Fuzhou 350108, China; 2 College of Forestry, Fujian Agriculture and Forestry University, Fuzhou 350002, China) Choosing suitable auxiliary and effective method is the prerequisite to accurately predict the spatial distribution of soil organic matter (SOM) in estuarine wetland. In order to achieve this purpose, a case study was conducted in the Minjiang Estuary Wetland of Fuzhou, southeast China. A total of 23 environmental factors were extracted by ArcGIS geostatistical analyst and remote sensing image analysis technique.Then, stepwise regression model and principal component analysis were used to screen the characteristic variables. At last a hybrid model of the support vector regression Kriging (SVRK) was proposed toanalyze the spatial variability of SOM, and compared with BP neural network Kriging(BPNNK) and regression Kriging (RK). The results showed that normalized vegetation index (NDVI), ratio vegetation index (RVI), perpendicular drought index (PDI), flow accumulation (FA) and sediment movement index (SMI) were significantly correlated with SOM, which had the higher coefficient of determination (2= 0.446) and the significant probability value (<0.000 1). Three principal components, explained at least 94% of the total variance, were extracted from these environmental factors by principal component analysis and used as characteristic variables.The spatial variability of SOM was affected by structural factors, showing a trend of “lower in the north and higher in the south”. Compared with RK andBPNNK,SVRK had the highest prediction accuracy, and more accurately reflected the spatial variability of SOM, can provide a methodological support for the study of spatial variability of SOM in the same or similar region. Estuary wetland; Soil organic matter; Stepwise regression;Support vector regression Kriging S156.8 A 10.13758/j.cnki.tr.2020.06.026 陈思明, 王宁, 秦艳芳, 等. 基于特征变量与支持向量机回归克里格(SVRK)法的湿地土壤有机质空间变异特征分析. 土壤, 2020, 52(6): 1298–1305. 福建省科技计划项目(2020J01831)和福建省教育厅中青年教师教育科研项目(JT180407)资助。 陈思明(1982—),男,福建厦门人,博士研究生,讲师,研究方向为遥感应用、城市林业、土地利用碳排放等。E-mail:wujingwujing0900@163.com2 结果与分析
2.1 土壤有机质及环境因子的统计特征

2.2 土壤有机质空间分布预测特征变量的选取

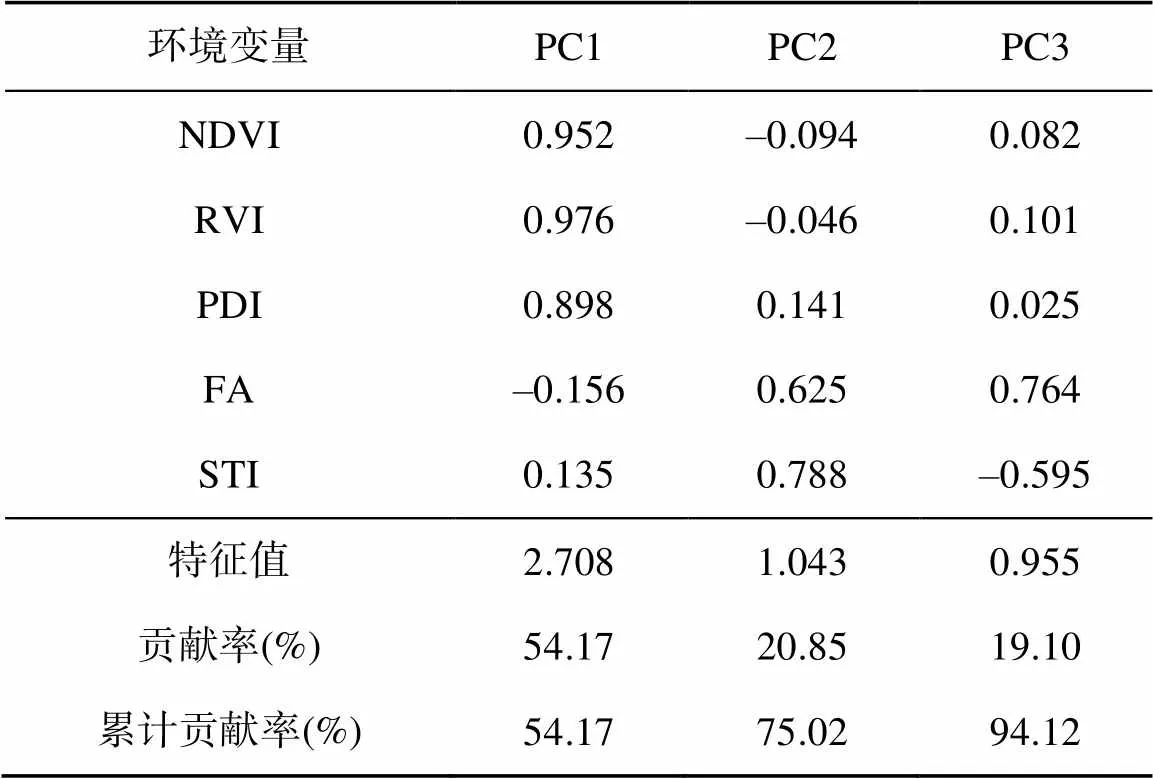
2.3 土壤有机质的空间异质性



3 讨论
4 结论

