基于碳约束的电网配送中心选址优化研究

王亚文

华北电力大学

0 引言

由于化石燃料等各种能源的大量消耗，产生大量的废气、废水等严重污染自然环境，加剧了温室效应，各国对此提出了各种低碳政策。我国2016年的《“十三五”控制温室气体方法工作方案》中提出：中国政府承诺2020 年碳排放强度降低18%，碳排放总量控制到稳定水平[1]。电力物流业作为我国经济发展的重要产业之一，产生的碳排放量占比达到了18．9%，因此发展低碳物流显得尤为重要。电网物流网络体系中存在物资存储地点多，配送路线迂回、交错及单程等运输问题[2]。及时准确地供应电网物资，才能确保电网企业安全可靠地运行、电网工程建设按期完成，电力行业才能稳定健康发展。在发展绿色物流的背景下，本文提出基于低碳约束的电网物流配送中心优化研究。

目前，考虑碳排放约束主要从碳税、碳限额、低碳经济方向研究。基于碳税建立双层需求不确定下的低碳配送中心选址模型[3]，为了降低物流网络的成本、碳排放和服务周期，提高客户对物流网络的满意度，研究了一种区域低碳的选址路径优化问题，并通过基于量子新的超启发式方法求解目标模型[4]。用改进动态惯性权重粒子群结合VNS 算法，解决以配送质押物的车辆运行总距离最小为目标的车辆路径问题[5]。基于冷链物流车辆配送节能减排背景, 建立以碳排放量最低为目标的配送路径优化模型, 运用蚁群算法进行路径优化求解[6]。基于碳税和碳限两种碳规则，构建有容量限制且带时间窗的车辆路径规划模型，并用遗传算法求解[7]。本文将采用改进粒子群算法求解选址问题。

本文的创新点：（1）构建了基于碳约束的二级电网配送中心选址模型；（2）改进免疫粒子群算法求解选址问题。

1 改进免疫粒子群算法

1.1 粒子群算法

粒子群算法是Kennedy 和Eberhart（1995）提出，利用群体迭代，粒子在解空间追随最优的粒子进行搜索。D 维空间中，该群由N 个粒子组成，第i个 粒 子 由 Xi=(xi1,xi2,…,xiD)T，速 度 表 示 为Vi=(vi1,vi2,…,viD)T和粒子个体经历过最好位置Pbest：Pi=(pi1,pi2,…,piD)T，还有种群所经历过最好位置，Gbest：Gi=(Gi1,Gi2,…,GiD)T。

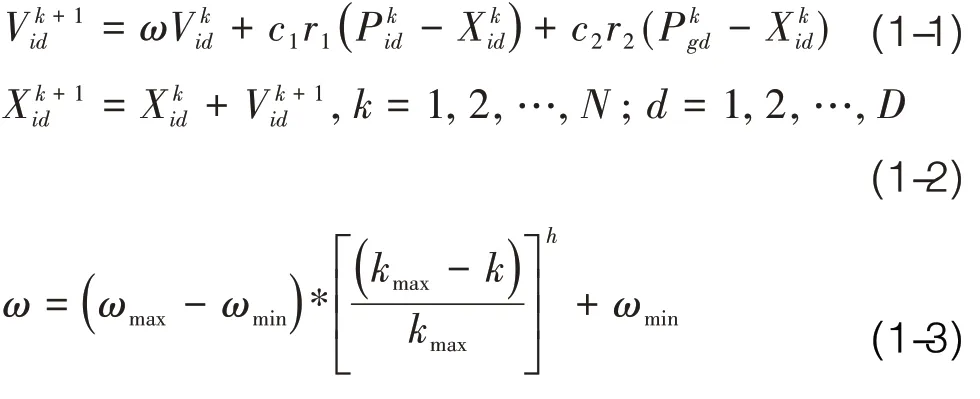
ωmax, ωmin分别代表最大和最小惯性权重系数，一般取值介于0．9 和0．4 之间。为提高算法的寻优能力，将非线性惯性权重系数和选择性变异策略应用于粒子群优化算法中（简称IPSO）成为新的改进粒子群算法。非线性惯性权重系数的更新是随着迭代次数、速度和位置的变化而非线性变化的，变化规律如式(1-3)所示。

1.2 改进免疫粒子群算法

将改进粒子群应用到免疫算法中的具体步骤如下：

（1）确定初始粒子群。确定粒子长度及抗原的位置；再调整学习因子、种群规模、记忆库容量等参数，随机生成初始粒子群。

（2）检验粒子是否满足边界要求。除去不满足边界位置要求的粒子，用新粒子来补充，重复这个过程。

（3）计算各粒子适应度和繁殖率。

计算每个粒子的适应度值并进行排序，适应度值为目标函数。

（4）粒子速度和位置更新

粒子的速度和位置的更新是指将位置超过边界、速度超过阈值的粒子重新调整到边界值和阈值范围内。

（5）免疫处理。主要是免疫选择、交叉、变异操作。使用变异概率对粒子的随机元素进行变异。

（6）产生新抗体。随机生成新粒子，进入新一轮迭代。

将改进免疫粒子群算法应用到基于碳约束的电网物流配送中心的二级选址求解优化中。选取的各级配送中心是在已有的备选配送中心中选取，当备选点被选中则作为配送中心，若没被选中则还是需求点。

2 建立模型

2.1 模型的基本假设

电力配送中心选址是一个多目标、多约束的非线性优化问题，备选点的物资需求配送量是决策变量。将结合电力物资特有的特点，构建两级电力物资配送中心选址数学模型，并作假设如下：

（1）将多类别物资看成一种物资，即将各物资的运输费用设定为统一值。

（2）配送中心的物资存储费用不考虑时间因素。

（3）备选点之间的配送距离设为直线距离。

（4）一个一级配送中心能向多个二级配送中心配送物资，但是一个二级配送中心只能接受一个一级配送中心的物资供给。同样，一个二级配送中心能向多个需求点配送物资，但一个需求点只能接受一个二级配送中心的物资供给。

（5）当备选点被选中，当地的物资需求则由当地配送中心负责，配送费用为0；当备选点没被选中，则该备选点即作为物资需求点。

（6）各备选配送中心的规模和容量能够满足其需求点的要求，不考虑扩建费用。

2.2 模型构建

基于上述假设条件，构建碳约束的二级配送中心选址优化模型，以物资运输成本、物资仓储成本、时间惩罚成本及碳排放成本之和为目标函数。

2.2.1 物资运输成本

物资运输成本包括一级配送中心到二级配送中心的物资运输成本、二级配送中心到需求点的物资运输成本，公式如式（2-1）。

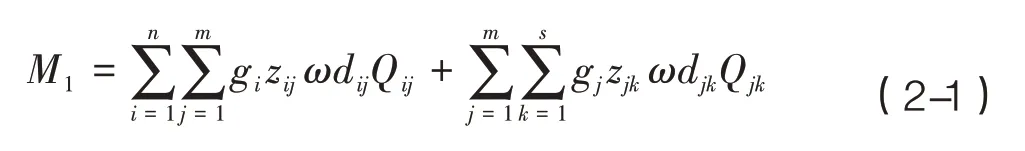
其中，

M1——运输总成本；

n——备选一级配送中心数量；

m——备选二级配送中心数量；

s——物资需求点的数量；

ω——运输配送率；

Qij——二级配送中心j 对一级配送中心的需求量；

Qjk——物资需求点对二级配送中心的需求量；

dij——一级配送中心i 到二级配送中心j 的距离；

djk——二级配送中心j 到物资需求点k 的距离；

gi——为0-1决策变量，备选一级配送中心是否选中；

gj——为0-1决策变量，备选二级配送中心是否选中；

zij——为0-1 决策变量，一级配送中心i 是否覆盖二级配送中心j；

zjk——为0-1 决策变量，二级配送中心j 是否覆盖物资需求点k。

2.2.2 物资存储成本

存储管理成本是指在配送中心存储及管理维护过程中管理物资的成本，主要包括物业管理费，库存管理人员的费用，资产折旧等。该项费用与物资存储量呈正向关系，物资存储量越大，则物资存储成本越高，其数学模型如式（2-2）。

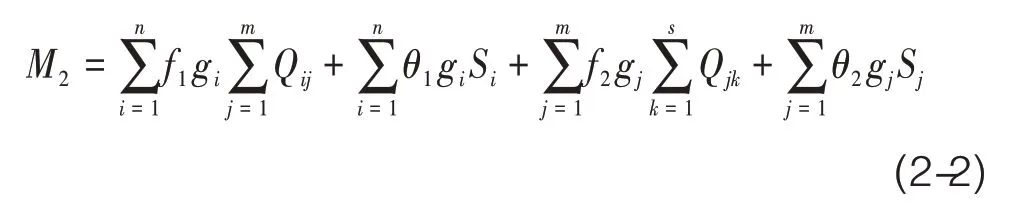
其中，

M2——物资存储成本；

f1——一级配送中心物资的存储率；

f2——二级配送中心物资的存储率；

θ1——一级配送中心平均每米仓储人工费用；

θ2——二级配送中心平均每米仓储人工费用；

Si——一级配送中心的有效库存面积；

Sj—— 二级配送中心的有效库存面积；

2.2.3 时间惩罚成本

时间惩罚成本是指配送中心在规定的服务响应时间内无法完成配送任务，按照需求方所等待的时间对配送中心进行惩罚。将配送服务响应时间转化为配送中心的配送服务半径，即对二级配送中心（或物资需求点）未在一级配送中心（二级配送中心）配送服务半径内的将被惩罚，通过惩罚率计算时间惩罚成本。计算公式如式（2-3）。

其中，

M3——时间惩罚成本；

ρ1——一级配送中心的服务惩罚费率；

ρ2——二级配送中心的服务惩罚费率；

R1——一级配送中心的服务半径长度；

R2——二级配送中心的服务半径长度；

δij——为0-1 决策变量，二级配送中心j 是否在一级i配送服务范围内；

δjk——为0-1 决策变量，物资需求点k是否在二级j配送服务范围内。

2.2.4 碳排放成本

碳排放成本与碳排放量成正比，可用单位碳排放成本与碳排放量的乘积表示。碳排放量主要有运营所产生的碳排放量、运输过程中产生的碳排放量，计算公式如式（2-4）：

其中，

M4——碳排放成本；

q1——备选一级配送中心i 固定的年CO2排放量；

q2——备选一级配送中心j 固定的年CO2排放量：

τ——运输工具（货车）的CO2排放量系数；

α——单位碳排放成本；

2.2.5 目标函数

综合上述分析，建立电力物资配送中心选址总成本最小化的目标函数，如式（2-5）。

其中，

M——电力物资配送选址的总费用；

α——碳排放成本

2.3 模型约束条件

电力物资配送中心选址目标函数约束条件如下：

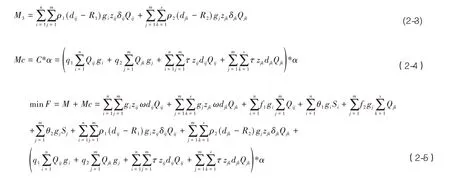
3 案例分析

案例中包含5 个地级市和15 个县级市，将地级市作为备选一级配送中心，县级市是备选二级配送中心，需求点是其中所有地级市和县级市，总共20个。考虑了碳排放量因素，将碳排放量转化为碳排放成本。根据碳市场交易价格，此处的碳排放成本为20元/t。运输过程中运输工具的燃料消耗是产生碳排放的主要原因，不同燃料的碳排放系数是不同的。因此，基于低碳约束，构建了以物流成本和碳排放成本之和最小化的目标函数。

通过改进免疫粒子群算法求解基于碳约束的选址问题，表1 为不同CO2系数下的选址成本，图1 为不同CO2系数选址成本对比图。碳约束下的选址方案见表2，碳约束的选址方案结果位置图见图2。

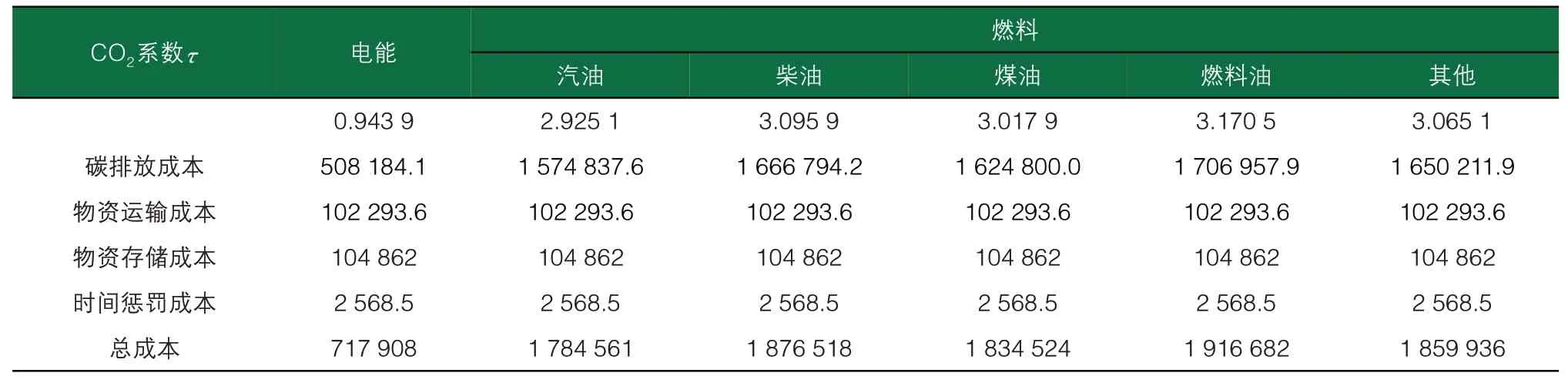
表1 不同CO2系数下的选址成本

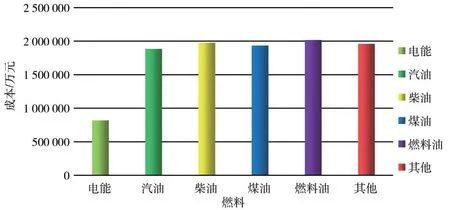
图1 不同碳系数下的选址成本对比图

表2 碳约束下的选址方案

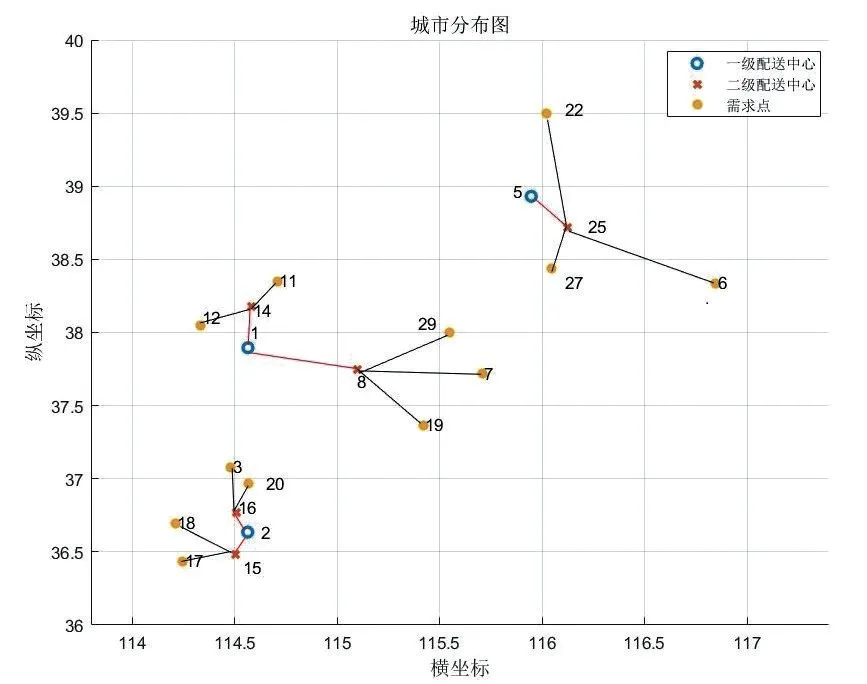
图2 碳约束的选址方案结果位置图

根据表1和图1可以看出运输工具燃料是以电能为动力，总成本最小，为717 908元，其中碳排放成本为508 184．1 元，物资 运输 成 本 为102 293．6 元，物资存储成本为104 862 元，时间惩罚成本为2 568．5 元，所产生的碳排放量最小，为响应碳减排政策，优选以电能为动力的运输工具进行配送。基于低碳约束的配送中心配送选址优化方案如表2所示，选址详细优化图如图2所示。

选中的一级配送有1，2，4，二级配送中心为7，14，11，12，18。有效控制配送中心的数量，科学地确定出配送中心的位置，能有效减少物流成本和碳排放量，提高物流服务效率。

4 结论

应用所构建的基于低碳约束的二级电网物流配送中心选址数学模型并用改进的免疫粒子群算法求解。计算结果表明，所构建的模型和运用的算法能有效地降低配送中心选址的总费用，提高物流效率，减少物流碳排放量。控制配送中心数量，有助于电网物资统筹管理和调配。本文所研究的内容具有一定的理论意义和实际意义，可为未来电网物流配送中心选址决策作依据。