基于视觉与非视觉效应的教室采光多目标优化

陈启宁，吴 蔚

(南京大学建筑与城市规划学院，江苏 南京 210093)

引言

许多研究表明天然采光不仅影响视看效果，也通过非视觉效应影响人体生理节律与健康[1]，包括影响褪黑激素分泌，引起睡眠障碍[2]，甚至诱发季节性情绪失调(SAD)、老年痴呆症等疾病[3]。进一步的研究显示，相较于视觉效应，非视觉效应在响应机理、影响因素、视看方向等方面都有所不同；即相同的建筑的朝向、室型比、窗墙比等设计因素对视觉和非视觉的影响也不尽相同。因此，营造出同时满足视看和非视看需求的优质天然光环境，需要将二者有机关联起来，统筹考虑[4]。

近年来，国际上关于采光视觉与非视觉效应两者的关联研究已经逐步开展。2017年，Maria等[5]提出一种基于人视点的采光视觉与非视觉联合评估工作流，利用三种新的天然光性能模型进行360°沉浸式空间评估。Dai等[6]开发了一种四通道可调LED光源混合方法，对照明的视觉与非视觉效应同时进行考虑。但这些研究仅针对特定背景和工况条件，没有考虑在实际设计过程中应用软件的多样性，大部分的研究停留在定性分析上，缺乏从视觉与非视觉两者量化联系入手的定量分析研究。因此，目前已有的研究成果尚不能在真实采光设计中开展起来。

在非视觉研究方面，课题组前期进行了有效昼夜节律区域百分比法和生物照度阈值法两种非视觉效应的计算机模拟评价方法研究[7, 8]，并在此基础上对医院病房的非视觉效应开展了量化研究[9]。目前的研究是进一步将视觉与非视觉效应有机联系起来，进行二者的耦合研究。本文尝试利用多目标算法，以南京市一个真实的学校教室为例，对天然采光的视觉与非视觉效应进行定量分析，对影响视觉和非视觉的设计参数进行耦合优化分析。

1 研究背景

多目标优化算法是一种同时对多个目标函数同时进行优化计算的方法，可实现多个优化目标的自动寻优[10]。多目标优化在建筑领域已有不少应用，可以根据采光、热舒适、能耗等具体的优化指标需求，调整设计参量，完成约束条件下多个优化目标的实现。如Carlucci[11]以室内眩光与热舒适指标为优化目标，运用遗传算法对意大利某建筑进行多目标优化；Negendahl等[12]以自然采光性能、能耗为目标，对建筑维护结构进行优化；周白冰[13]以多种自然采光性能评价指标作为优化目标，研究寒地多层办公建筑空间的多目标优化。由此可见，多目标算法能够较好地同时分析影响室内天然光的视觉和非视觉因素，进行优化选择。

1.1 视觉与非视觉效应的多目标优化方法

本研究所采用的视觉与非视觉采光多目标优化方法由3部分组成，工作流程见图1。

1) 生成参数化模型：实现设计参量与视觉、非视觉采光优化目标的映射，避免重复建模。

2)进行优化计算：得出同时满足视觉、非视觉采光需求的设计参量的较优取值区间。

3)筛选优化方案：对优化计算结果进行可视化显示与量化分析。

该方法基于Rhino & Grasshopper参数化平台，以Radiance和Daysim为采光计算引擎，整合Honeybee等性能模拟插件与Python编程语言，结合多目标优化插件Octopus，实现视觉与非视觉采光的耦合优化。其实质是将采光的视觉与非视觉评价指标同时考虑，通过优化算法进行多次迭代计算，得出同时满足视觉与非视觉优化目标的较优解集范围。最后应用参数化模型，将结果数据可视化反馈，供设计人员根据项目的具体视觉和非视觉采光需求进行筛选，为健康光环境营造提供决策支持。

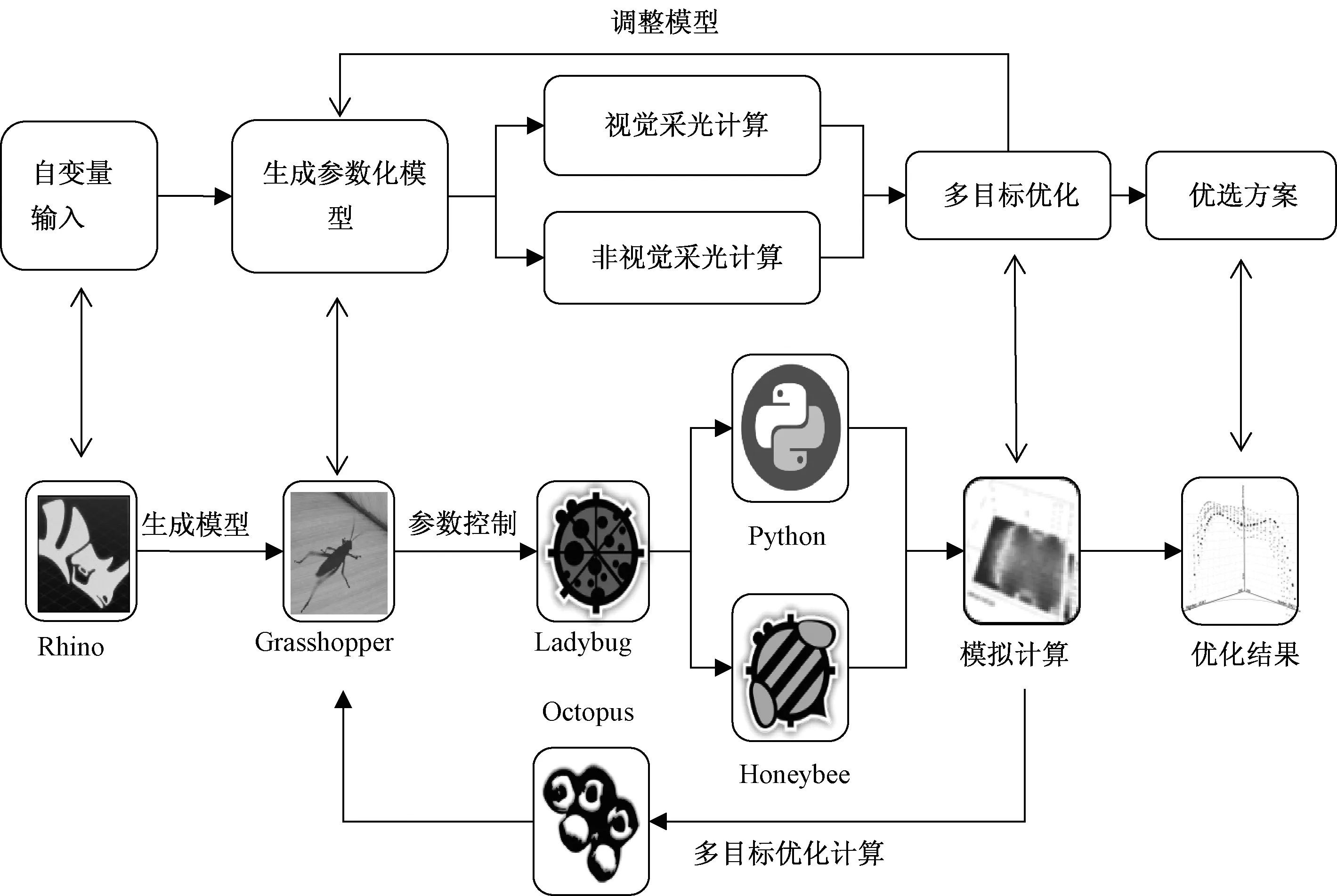
图1 视觉与非视觉效应多目标优化流程图Fig.1 Multi-objective optimization flow chart of visual and non-visual effects

1.2 评价指标、模拟平台与计算程序

1)评价指标。视觉指标采用天然光自主参数(Daylight autonomy)和有效天然采光照度(Useful daylight illuminance)。这两项指标作为全年动态采光评价指标，可有效反映天然光随时间变化而变化的情况，已在不少研究中得到验证[14, 15]。

非视觉指标采用Konis提出的有效昼夜节律区域百分比(circadian effectivearea，CEA)和昼夜节律频率(Circadian Frequency，CF)指标[16, 17]。

a)全年刺激频率(Stim.freq，SF)加入了对感光史的考虑[18]，可量化某一时间窗口内的光照刺激有效性，较为直观地评价和预测室内天然光产生的非视觉效应。该指标在每个网格点上以偶数增量排列多个向量，以表示视看方向。一般指定8个向量，可以增加向量数以获得更高的精度。

b)昼夜节律频率(Circadian Frequency，CF)可用于评估采光设计满足WELL标准中使用日光的昼夜照明要求的程度。昼夜节律频率在这里被定义为在特定的日分析周期内，当一个给定的视向量满足或超过以褪黑素照度EML(Equivalent Melanopic Lux)为单位的给定光刺激阈值时，年度分析周期内的天数百分比。因此该指标可以在一定程度上反映光源对使用者的警觉性、睡意和眼疲劳的影响[19]。

2)软件平台与程序编写。

本文中所涉及的参数化建模使用建模软件Rhino以及可视化编程平台Grasshopper。计算脚本使用Python语言编写，并通过GHpython插件与Grasshopper平台进行关联。采光计算模拟与优化使用Grasshopper平台上的开源建筑性能模拟插件Honeybee以及多目标优化插件Octopus。其中，Honeybee插件以Daysim及Radiance为采光模拟引擎，内置多种常用CIE标准天空模型，并且可以定义多种材料光学性质，其采光模拟的准确性已经得到相关研究[20]验证。

为实现视觉与非视觉采光评价指标的优化计算及模拟数据实时记录两方面的功能，本文基于GHpython编写了一套Grasshopper平台的辅助计算程序。程序由参数输入模块，采光模拟模块，优化计算模块三部分组成。其中，参数输入模块通过调节设计参量输入值产生不同的参数化模型；采光模拟模块通过读取气象数据，计算非视觉照度转换系数、所选分析时段内的天空类型，实现视觉与非视觉的采光模拟计算；优化计算模块通过多目标算法进行迭代运输，得出同时满足视觉与非视觉需求的设计参量较优取值区间。图2所示是全部优化模拟计算程序的组合图，可以通过该程序对视觉与非视觉采光的评价指标进行模拟、耦合优化和量化分析。

图2 非视觉模拟计算程序图Fig.2 Non-visual analog program diagram

2 多目标优化设计研究

本研究选取南京市某中学的一个真实教室为对象展开模拟实验，在研究团队前期的实地测量研究中，该学校教室符合《中小学建筑设计规范》(GBJ 50099—2011)和《建筑采光设计标准》(GB 50033—2013)的要求[21, 22]。该教室进深为7.5 m，开间为9 m，层高为3.5 m，窗地比为0.24，双侧采光，具体尺寸如图3所示。本文所使用的室内材质的光学属性参数是根据实地测量所得，如表1所示。

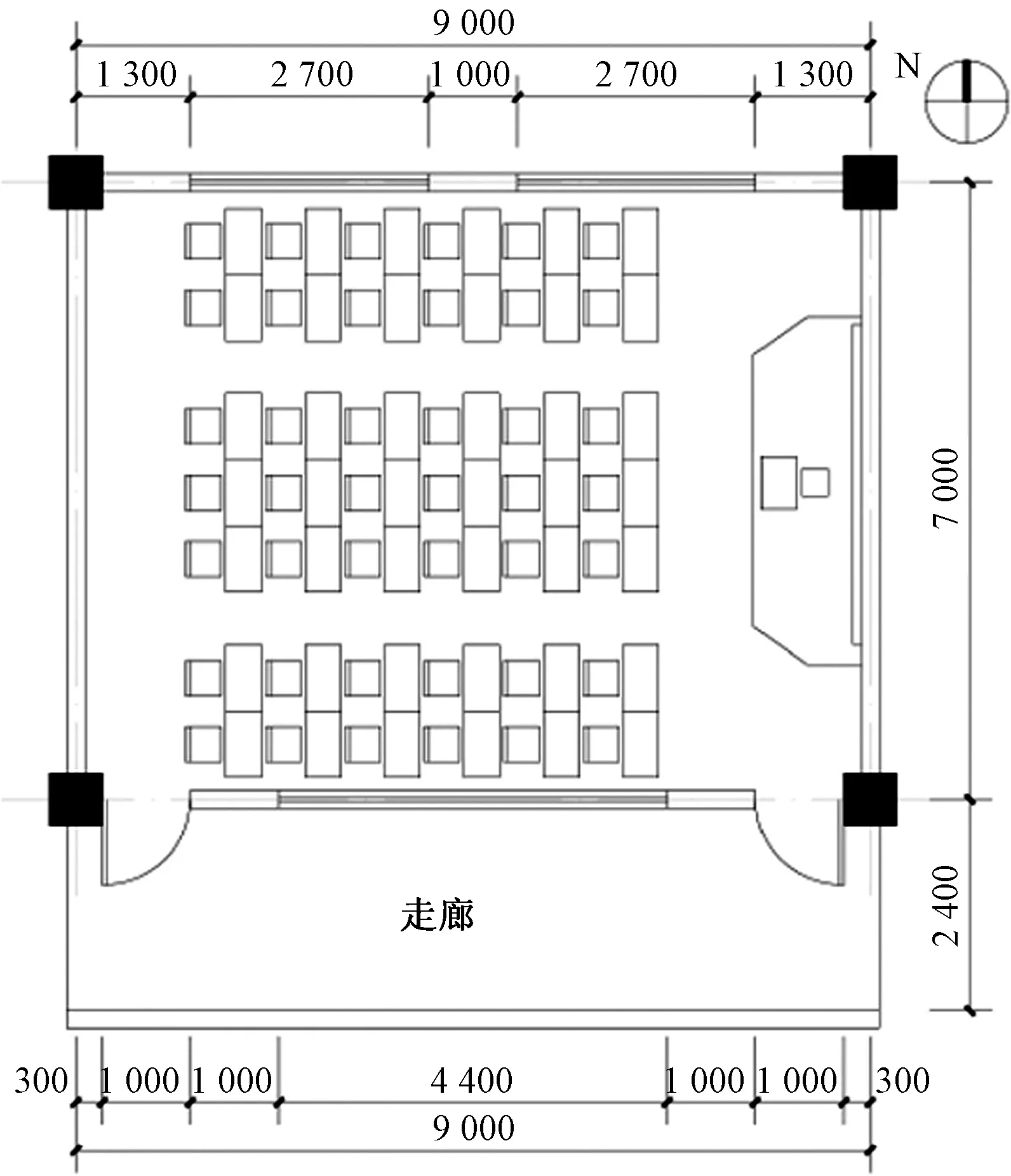
图3 教室平面图 Fig.3 Plan of the example classroom

表1 材料参数设置Table 1 Setting of material parameters

2.1 优化设计参量与优化目标

考虑到模拟计算和参数化建模的复杂度，本文仅选取窗台高、窗地比、窗户间距(两窗的垂直中心线间距)作为优化中的设计参量。为保证优化计算得出的空间形态结果符合相关规范，模拟时需要给设计参量设定取值范围。根据规范，教室开窗面积在窗地比应大于0.2，因此将窗户宽度、高度取值设定在1.8～2.3 m之间，窗台高度在0.9～1 m之间。由于中小学教室前端的侧窗窗端墙长度不应小于1 m，考虑到窗户宽度的取值，将窗户间距的取值设定在3.0～3.5 m之间。考虑到采光模拟的误差，最终教室采光视觉与非视觉优化设计参量取值的约束条件如表1。

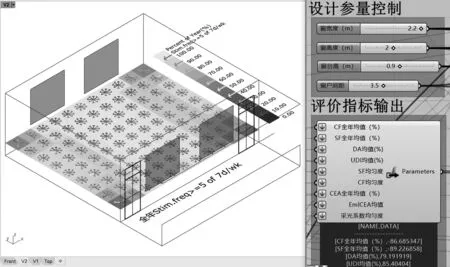
图4 教室参数化模型Fig.4 Parametric model of the example classroom

表2 设计参量取值Table 2 The value of design parameters

为同时对视觉与非视觉采光进行优化，选取视觉采光评价指标DA、UDI；非视觉采光评价指标全年刺激频率(Stim.freq，SF)、昼夜节律频率(Circadian Frequency，CF)；各指标取所有测点的平均值作为优化的目标函数。其中非视觉指标的分析时段依据WELL标准中规定的最小标准，取为9:00—13:00[23, 24]。

2.2 建立参数化模型

为实现设计参量与优化目标之间的映射，需要借助参数化模型进行性能模拟。在Rhino & Grasshopper平台建立如图4所示的教室参数化模型，实现窗台高、窗地比、窗户间距、窗户宽度和窗户高度的动态调节。当任意设计参量改变时，Honeybee插件调用Radiance和Daysim内核对参数化模型进行实时采光模拟，自动反馈模拟结果，避免重复建模，并实现空间形态信息的评价指标的关联。

Honeybee插件进行采光计算时，需要先将Rhino模型转换为Honeybee Zone模型，再设置室内材质。Honeybee可提供Radiance材质库的调用。

2.3 多目标优化模拟

采用Octopus插件基于HypE Reduction算法进行优化计算，多目标优化的程序图如图5所示。将设计参量与优化目标分别输入到Octopus计算模块，运行多目标优化算法，驱动采光模拟程序对不同设计参量组合进行多次迭代计算，对优化目标进行权衡，寻求较优的设计参量组合解集。

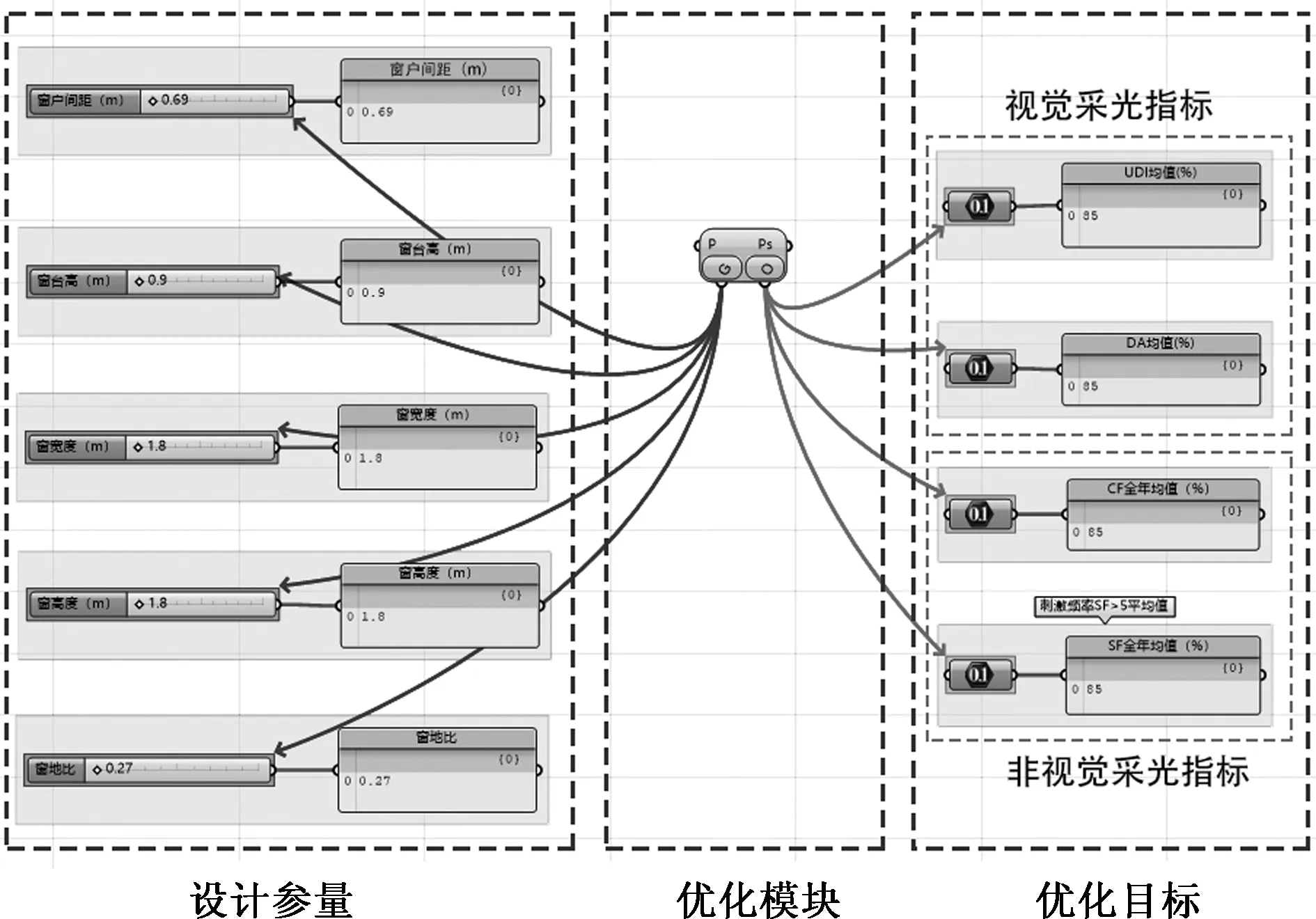
图5 多目标优化算法程序图Fig.5 Multi-objective optimization algorithm program diagram

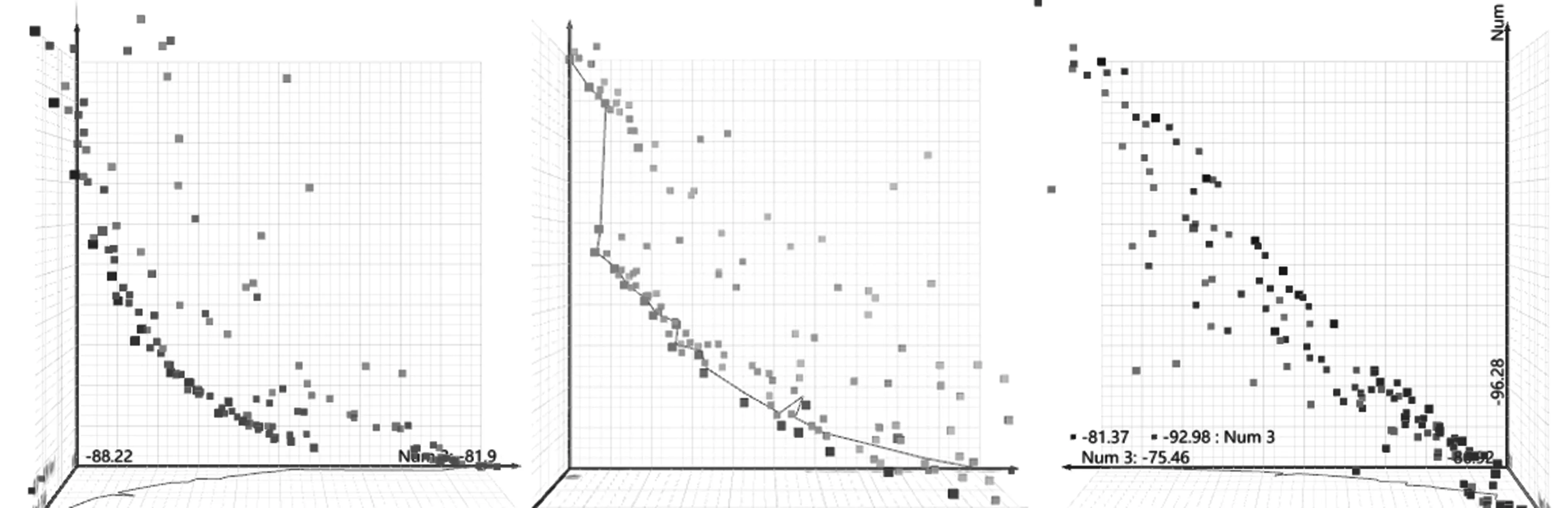
图6 Pareto空间分布图Fig.6 The spatial distribution of the Pareto solution set

本次优化共有3个变量，4个目标函数参与计算，Octopus插件的具体优化参数设置如表3所示。参数设置时需要综合考虑解集的多样性和所需的计算量，既要避免丢失最优解，也要避免过早收敛，局限于局部最优。优化计算完成后，可以在算法给出的优化目标解集中进行筛选，以进一步得出合适的设计参量取值。

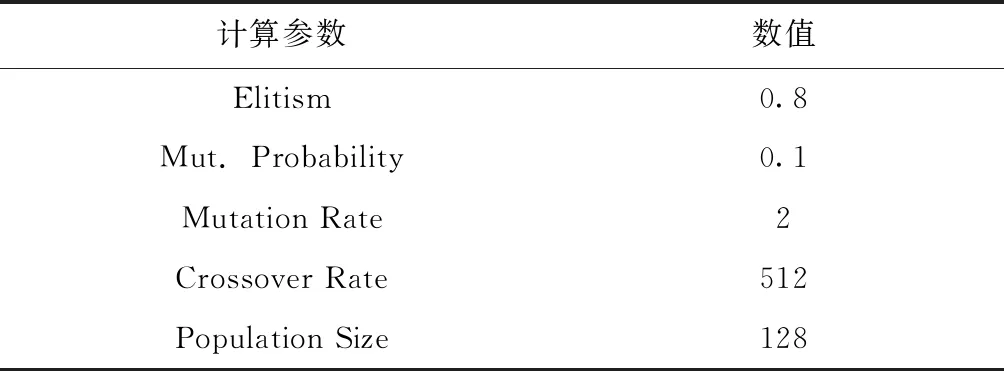
表3 多目标优化参数设置Table 3 Parameter setting for multi-objective optimization

3 分析与讨论

本次优化经过35次的迭代计算，共耗时70 h，总计获得695组非支配解集的数据。计算得到的Pareto解在三维坐标轴内的分布如图6所示。连接大部分Pareto最优解所组成的曲面即为Pareto前沿面，其在二维方向上可形成Pareto前沿，具有较好的收敛性。将优化计算的结果数据通过GHpython脚本自动记录并整理，全部数据分别导入Excel和Spss软件中，进行进一步的数据分析。

3.1 优化结果的验证

对第35次迭代的Pareto解集进行分析，根据模拟得出的结果，共有32个非支配解。选取其中各项优化指标较好的4组解作为代表性的优化方案，每个解对应的优化目标、设计参量如表4所示。

将表4中的优化方案与原始教室的视觉与非视觉指标进行对比，绘制成如图10所示的折线图。通过比较优化前后各指标的取值可以发现，经过优化，视觉与非视觉指标同时得到了提升。其中，第3组解在4项优化目标之间形成了较好的平衡，相较于原始方案，其视觉指标中DA提升16.69%，UDI提升1.05%，非视觉指标中SF提升10.34%，CF提升9.34%。

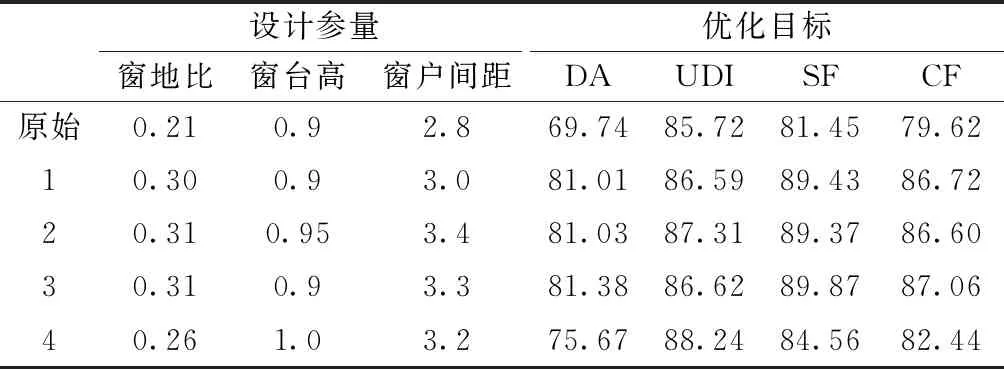
表4 多目标优化设计实验优化方案记录Table 4 Record the experimental optimization scheme of multi-objective optimization design

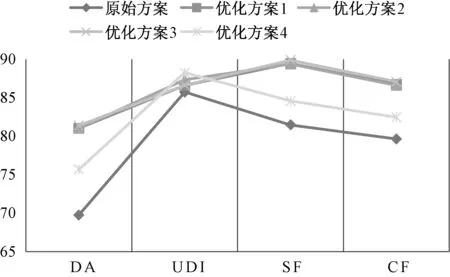
图7 优化前后视觉与非视觉采光水平对比Fig.7 Comparison of visual and non-visual lighting levels before and after optimization

3.2 量化分析

为了量化非视觉指标与视觉指标之间、非视觉指标与设计参量之间的关系，本研究采用统计学中常用的相关性分析方法及线性回归分析方法对进行分析，并通过优化数据的分布情况，得出各设计参量的较优取值区间。

1)相关性分析。将数据导入SPSS软件，对昼夜节律频率(Circadian Frequency，CF)与其他优化目标及设计参量进行相关性分析，结果如表6所示。表中的Pearson相关性表示相关关系的强弱情况，Pearson系数0.8～1.0为极强相关；0.6～0.8为强相关；0.4～0.6为中等程度相关；0.2～0.4为弱相关；0.0～0.2无相关。相关性分析表明，CF全年均值与窗地比、DA均值、SF全年均值为正相关，与窗台UDI均值为负相关关系。

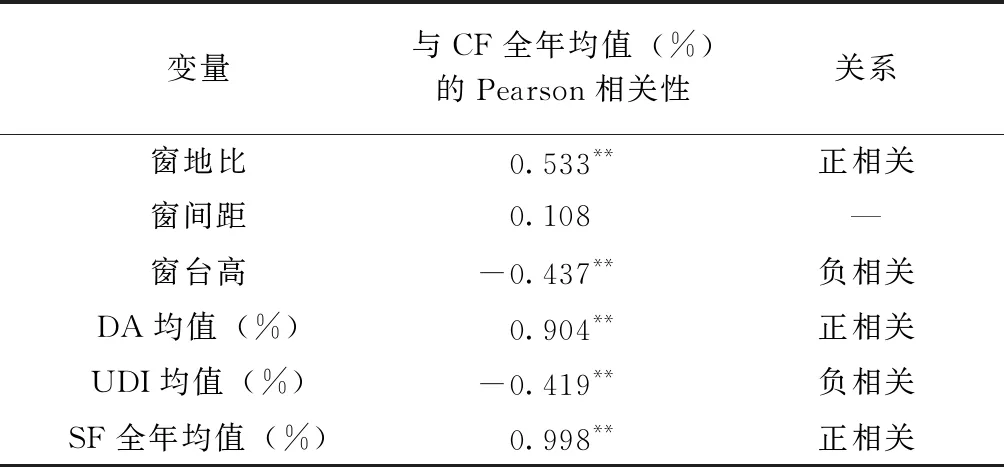
表5 昼夜节律频率相关性分析Table 5 Correlation analysis of Circadian Frequency (CF)

表6 昼夜节律频率(Circadian Frequency，CF)线性回归结果Table 6 Linear regression results of Circadian Frequency (CF)

2)线性回归分析。在SPSS软件中将窗地比、窗间距和窗台高作为自变量，将昼夜节律频率CF作为因变量进行线性回归分析以及自动线性建模，得到线性回归模型，结果如表7所示。

从表7可知，模型R2值为0.640，意味着窗地比、窗间距和窗台高可以解释CF全年均值的64.0%变化原因。窗地比的回归系数值为24.628(t=7.432，P=0.000<0.01)，意味着窗地比对CF全年均值产生显著的正向影响关系；窗台高的回归系数值为-8.971(t=-6.111，P=0.000<0.01)，意味着窗台高对CF全年均值产生显著的负向影响关系，与相关性分析地结果相同。

对模型进行F检验时发现模型通过F检验(F=27.285，P=0.000<0.05)，可以得到模型公式：CF全年均值=80.849+24.628×窗地比+13.560×窗间距-8.971×窗台高。基于该公式可对CF全年均值进行预测。

3)设计参量的较优区间分析。将数据导入Excel，以设计参量为横坐标，以优化目标在较优区间的内的取值为纵坐标，生成散点图，通过散点图的分布情况，可以直观得出各自变量的较优区间。如表5所示，筛选全年刺激频率Stim.freq>85%时的设计参量取值。对于全年刺激频率SF和昼夜节律频率CF，当窗地比的取值在0.25～0.3；窗台高取值在0.9～0.95；窗户间距取值在0.4～0.45时，两者的数值始终在85%以上。对于DA，当窗地比的取值在0.25～0.3；窗台高取值在0.9～0.95；窗户间距取值在0.4～0.45时，DA值一直稳定在80%以上。对于UDI，当窗地比的取值在0.25～0.2.7；窗台高取值在0.95～1.0；窗户间距取值在0.4～0.45时，UDI值始终保持在87.5%以上。

根据以上分析结果，设计参量的较优区间为：窗地比0.25～0.3；窗台高0.9～0.95；窗户间距0.4～0.45。

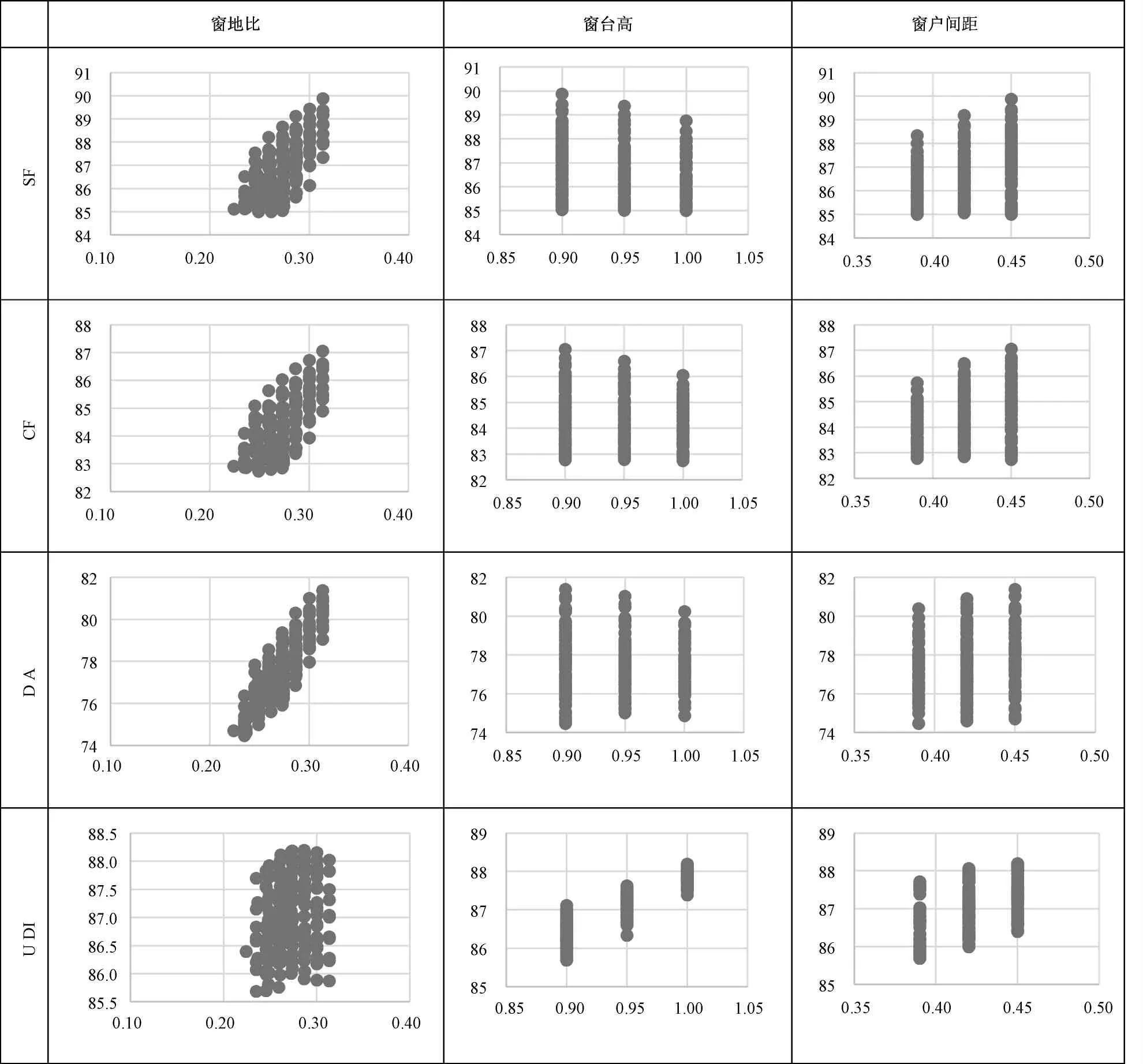
表7 不同设计参量与优化目标散点分布图Table 7 Different design parameters and scatter distribution of optimization targets

3.3 实验结论

以南京地区气象数据为背景，进行教室采光视觉与非视觉优化实验，结果表明，多目标优化方法能够同时对教室的视觉与非视觉天然采光进行优化，结合模拟数据可得出以下几点结论：

1)南京地区光气候条件下，为同时保证视觉与非视觉的采光水平，教室采光应当在符合规范要求的情况下，适当增大窗地比。

2)对模拟数据进行相关性分析，发现CF全年均值与窗地比有显著的正相关关系；与窗台高有显著的负相关关系；与DA均值有显著的正相关关系；与UDI均值有显著的负相关关系；与SF全年均值(%)有显著的正相关关系。

3)对模拟数据进行回归分析，发现窗地比、窗间距、窗台高与昼夜节律频率CF之间存在线性相关关系，模型公式为：CF全年均值 =80.849+24.628×窗地比+13.560×窗间距-8.971×窗台高。

4)对模拟数据进行散点图分布分析，总结出可使得室内视觉与非视觉采光同时达到较好的效果设计参量区间：教室的窗地比取值在0.25～0.3；窗台高取值在0.9～0.95，窗户间距取值在3.2～3.5。

4 分析与讨论

本文利用多目标算法实现了视觉与非视觉采光的耦合优化。以南京某中学教室为例，通过优化模拟实验验证了优化方法的应用效果。同时，通过对模拟数据进行统计分析，得出了教室采光的视觉指标、非视觉指标与不同设计参量之间的量化关系。

在研究中发现，在采用基于Octopus插件内置的HypE Reduction算法进行优化计算时，当设计参量值域较广时，时常会出现提早收敛，无法得出Pareto解集的情况。此外，由于Honeybee插件限制，高精度的全年动态采光模拟计算耗时较长，因此本次模拟仅使用默认参数，精度较低，如有条件可展开数值模拟与实测数据间的对比。

目前，非视觉效应的采光照明研究还处于初级阶段，很多相关研究都有待进一步开展，如不同天然光环境因素对视觉与非视觉效应采光的耦合影响规律、更精准的评价标准等。限于研究周期、实验场地等条件，本文仅进行了计算机模拟研究，后续工作将结合实地测量进一步展开对视觉与非视觉的联合研究。多目标优化算法本身也具有较大的优化空间，选用合适的数据结构和计算规则可以提高算法的计算速度和效率。在后续研究中将探索并尝试使用不同的优化算法进行计算，以提升视觉与非视觉耦合优化的效率和准确性。