嵌岩抗拔桩荷载-位移曲线拟合模型的对比分析

崔贵云 陈开伦 杨柏 赵珊珊 黄翔

（1.中交第一公路勘察设计研究院有限公司，西安710000；2.西南交通大学地球科学与环境工程学院，成都610031；3.桂林电子科技大学建筑与交通工程学院，广西桂林541004；4.桂林理工大学 土木与建筑工程学院，广西桂林541004）

抗拔桩作为一种承担拉力的基础形式在桥梁建设中较为常见。对于抗拔桩的极限承载力的确定，TB 100093—2017《铁路桥涵地基和基础设计规范》与JTG D63—2007《公路桥涵地基与基础设计规范》参考纯摩擦抗压桩承载力的计算方法，以折减系数考虑抗拔效应进行桩基抗拔承载力的计算，但一些研究表明规范值与现场实测值相比偏于保守［1-3］。通过现场试验获取抗拔桩极限承载力值或根据规范计算是目前较为常用的承载力获取方法。除此之外，数学模型法也是判定极限承载力的有效方法之一。通过数学函数模型描述荷载-位移曲线，选定较为理想的函数关系，重新绘制荷载-位移曲线，根据函数特征值计算极限承载力。蒋建平等［4］研究发现Weibull数学模型能很好地拟合PHC桩抗拔荷载-位移曲线。郭楠等［5］通过现场试验研究发现双曲线和幂函数模型比较适合软岩地基中布袋桩的抗拔极限承载力预测。吴彤等［6］用幂函数模型较好地拟合了冻土区管桩的上拔荷载与位移曲线。崔强等［7］用双曲线模型拟合了强风化岩中挖孔基础抗拔的荷载-位移曲线。

综上所述，不同的抗拔桩基类型及不同的地层条件下，描述抗拔桩荷载-位移曲线的数学模型各异。本文采用不同数学模型分别描述风化砂岩层中抗拔桩实测荷载-位移曲线，研究各数学模型的适用性和准确性。

1 试桩试验概况

试验场地位于我国西南地区一处山体斜坡台地，试桩地层条件如图1所示。试桩为机械旋挖成孔。试桩桩身混凝土强度等级为C30。试桩平面布置如图2所示，试桩尺寸及嵌岩情况见表1。

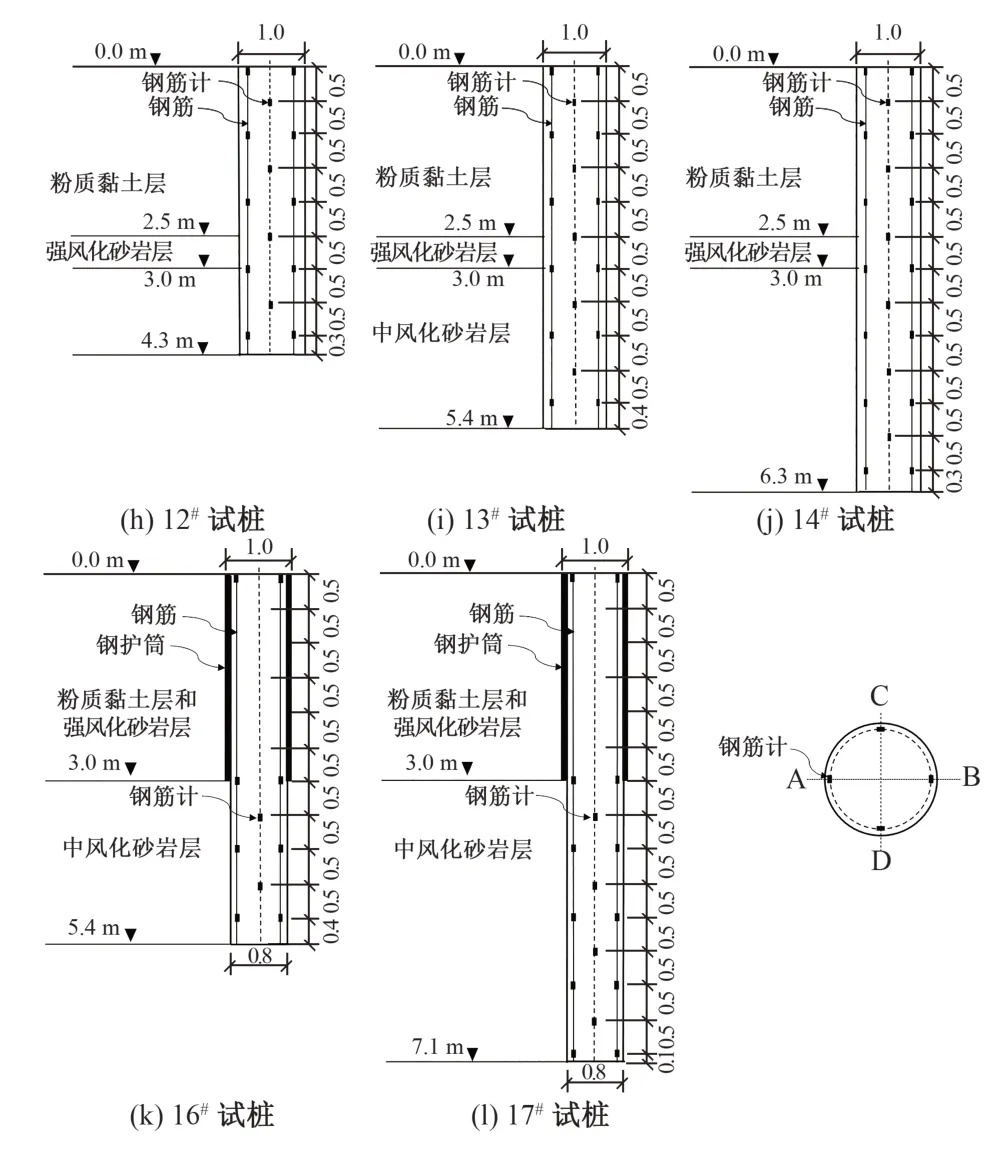
图1 试桩岩土层剖面图

图2 试桩平面布置图

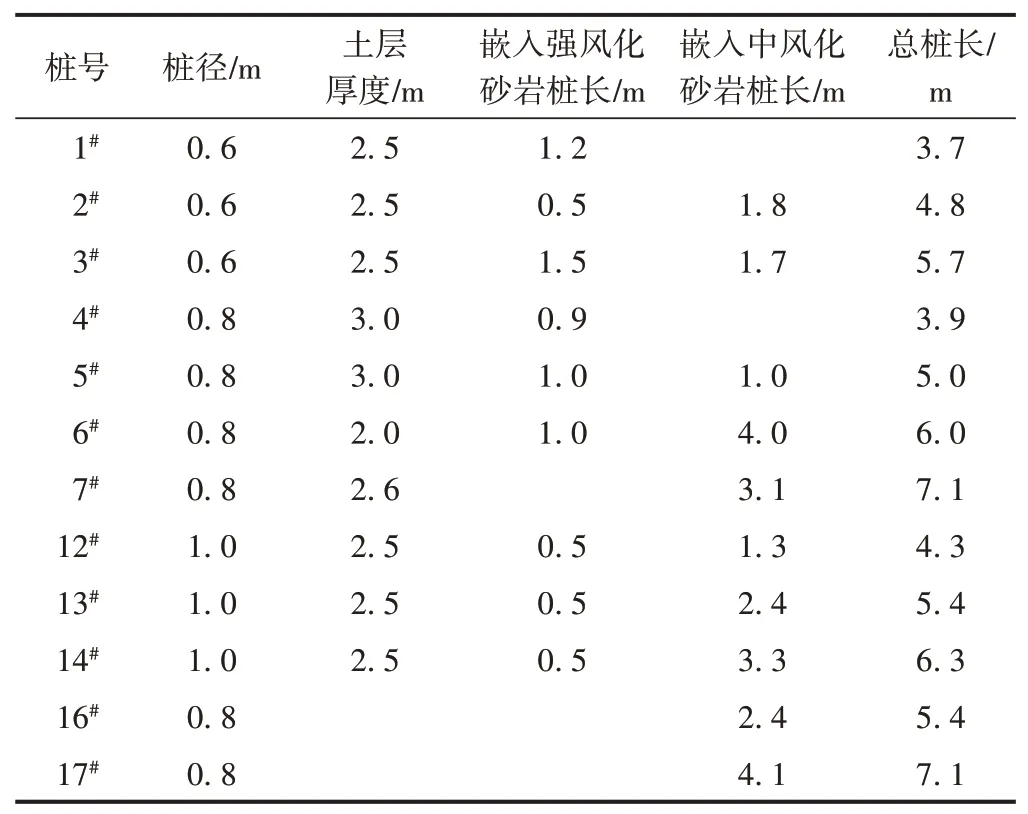
表1 抗拔桩尺寸表

试验采用JGJ 106—2014《建筑基桩检测技术规范》推荐的慢速维持荷载加载法加荷，现场单桩极限载荷试验装置见图3。试验过程与文献［8］一致。

图3 试验装置

试验得到的试桩测试结果见表2。由表2可知，12根试桩中，只有3#试桩未达到极限破坏，其他11根试桩满足破坏条件［2］，可获取其极限抗拔荷载和对应的桩顶位移值。

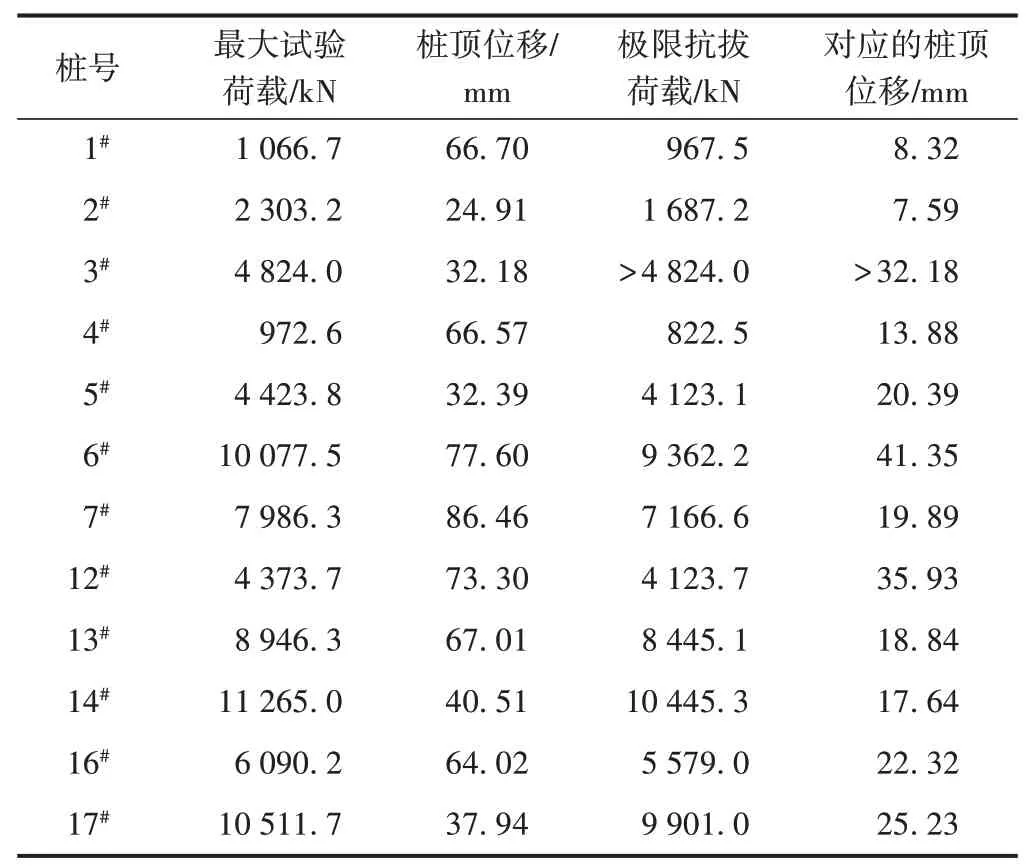
表2 试桩测试结果表

2 试桩实测荷载-位移曲线拟合比较

在众多描述抗拔桩荷载-位移曲线的数学模型中，双曲线模型、指数函数模型和幂函数模型的参数较少，简单方便而被广泛应用。

双曲线函数模型关系式为

幂函数模型关系式为

指数函数模型关系式为

式中：S为桩顶位移；Q为桩顶荷载；a，b为常数。

对于风化砂岩层中的抗拔桩，本文采用上述3种数学模型拟合现场试验中试桩的荷载-位移曲线，与实测曲线比较，结果见图4。

由图4可知，双曲线模型拟合现场试验中抗拔桩的荷载-位移曲线的复相关系数R2为0.963 9～1.000 0，平均值为0.983 0，拟合较好；幂函数模型的R2为0.677 8～0.997 4，平均值为0.870 0；指数函数模型的R2为0.873 1～0.997 8，平均值为0.954 0；双曲线模型对风化砂岩层中试桩上拔荷载-桩顶位移曲线拟合精度最高，指数函数模型次之，幂函数模型相对较差。用各试桩荷载-位移曲线拟合得到的双曲线函数计算试桩的极限承载力，分别与极限承载力实测值和最大试验荷载比较，结果见表3。

图4 数学模型拟合试桩上拔荷载-桩顶位移曲线比较

由表3可知，通过双曲线函数计算得到的极限承载力略高于实测值和最大试验荷载。不考虑未达到极限破坏的3#试桩，极限承载力预测值与实测值的比值为1.11～1.58，平均值为1.25，标准值为1.32；极限承载力预测值与最大试验荷载的比值为1.02～1.44，平均值为1.12，标准值为1.18。可以对双曲线函数得到的极限承载力除以1.32进行折减得到相对准确地试桩极限抗拔承载力，据此可以算出3#试桩的极限抗拔承载力约为5 222.5kN。

数学模型法通过数学函数描述试桩的荷载-位移曲线，根据函数特征值计算极限承载力，得到的值往往与实测值存在偏差，一般需要对计算值进行适当的折减，就本文风化砂岩层抗拔桩而言，可以对抗拔桩的计算值除以1.3折减，折减后的计算值更接近实测值，对于未达到极限破坏的试桩的极限承载力的预测更为准确。

3 归一化荷载-位移双曲线模型分析

为了降低多根试桩实测荷载-位移曲线的离散性，文献［9-11］提出了归一化荷载-位移双曲线模型描述荷载-位移曲线，即

式中：P为现场试验中的各级上拔荷载，kPa；PU为现场试验实测极限抗拔承载力，kN。

对试桩的荷载值做归一化处理，得到各试桩的归一化荷载（P/PU），分别对试桩的归一化荷载与位移作散点图，用MATLAB拟合得到双曲线函数系数均值和95%置信水平区间上下限值，见表4。

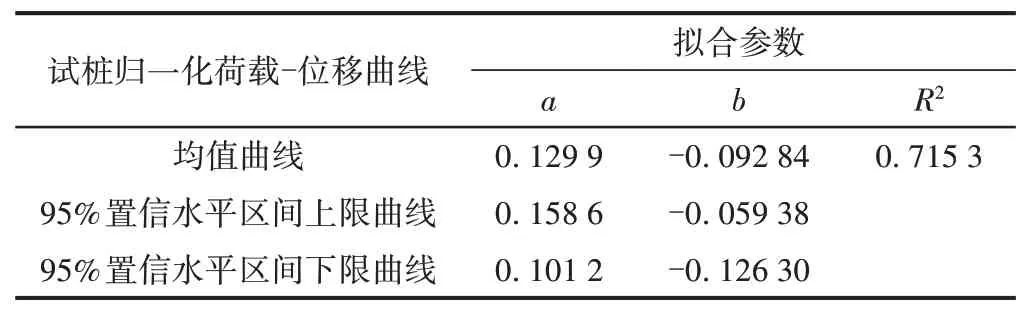
表4 抗拔桩归一化荷载-位移曲线双曲线模型拟合参数

双曲线函数模型拟合归一化荷载-位移曲线见图5。可知，大多数试验点位于上下限曲线之间，以上限曲线计算得到的极限承载力偏高，而以下限曲线计算得到的极限承载力偏安全，就工程的安全角度考虑，采用下限曲线计算风化砂岩层中抗拔桩的承载力是合适的，95%的情况是偏于安全的。

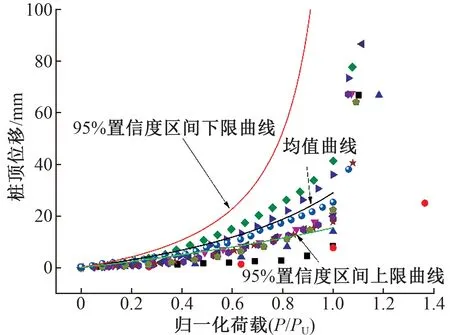
图5 双曲线函数模型拟合归一化荷载-位移曲线

鲁先龙［12］、崔强等［7］对每根试桩的荷载做归一化处理，获得各试桩的归一化荷载-位移关系曲线，用Phoon双曲线模型拟合，统计分析参数a和b，得到参数a和b的均值、95%置信水平区间上下限值，将参数代入模型公式，与实测曲线比较。本文对各试桩的荷载做归一化处理后，对各试桩试验点用Phoon双曲线模型进行拟合，直接得到了均值曲线和95%置信水平区间上下限曲线，相对而言节省了大量工作。

4 结语

双曲线模型对风化砂岩层中抗拔桩的上拔荷载-桩顶位移曲线拟合精度最高，指数函数模型次之，幂函数模型相对较差；采用双曲线模型预测嵌岩抗拔桩极限承载力，其预测值与实测值的比值为1.11～1.58，平均值为1.25，标准值为1.32；双曲线函数计算得到的极限承载力取1.3折减系数后，与实测值更为接近；采用归一化荷载-位移曲线双曲线模型下限曲线函数计算风化砂岩层中抗拔桩的承载力是合适的，95%的情况是偏于安全的。

本文的研究结果主要针对风化砂岩层中的抗拔桩基础，可以用于相似地层条件的抗拔桩承载力预测，对于其他地层条件是否适用有待进一步的研究分析。