BDS伪距单站定位计算及精度分析

干坚定，周 适，段太生，郭 平，晏 勇，刘立正

（1.中铁二局第五工程有限公司，四川 成都 610091；2.中铁二局集团有限公司，四川 成都 610031）

北斗卫星导航系统（BDS）最后一颗全球组网卫星（GEO卫星）已于2020年6月23日9：43在西昌卫星发射中心成功发射，这是由我国自主研发的卫星导航系统。对于全球导航卫星系统（GNSS）而言，GPS虽然仍是当前技术最先进和最成熟的导航定位系统，但BDS通过近3年来高密度的卫星发射，目前已具备和GPS共同作用、兼容并存的实力。从卫星数量和卫星类型上看，北斗的卫星数量和亚太地区的卫星分布比GPS更具优势，国内大量专业人士对BDS进行了相关深入研究。BDS即将组网完成，极大地增强了国人的自信心和民族自豪感，也激发了众多相关从业人员学习和研究BDS的兴趣。

1 相邻历元相位平滑伪距的数学模型

杨元喜等[1]提出，对北斗所有卫星进行统计，北斗B1I和B2I伪距野外测量的精度约33cm，B1和B2载波相位野外测量的精度约2mm。由于载波相位观测的精度远高于伪距观测[2]，因此采用伪距值进行单站定位计算时，有必要对伪距值进行平滑处理。伪距平滑的成熟算法包括载波相位平滑伪距算法和基于卡尔曼滤波的伪距平滑算法[3]。文章采用简易数学公式计算，BDS共设为3个频率，由于外业使用的接收机只采集B1、B2两个频率的观测数据，因此文章中的数学模型是针对北斗双频（B1、B2）展开的。对BDS不同频率分别列出伪距平滑公式，由于相邻历元时间较短，因此伪距中包含的噪声（电离层延迟、对流层延迟、多路径效应）可以忽略不计，整周模糊度N也可消去，具体公式如下[4]：

同理，可得B2频率下的各参数含义。利用相位平滑后的伪距进行后续单站定位计算，若监测到载波相位发生整周跳变，则相关历元不采用相位平滑的伪距值，而采用原始伪距观测值。

2 BDS单站单历元定位的数学模型

在t历元时刻，接收机共接收到n颗北斗卫星，通过北斗广播星历文件可计算每颗北斗卫星的空间坐标，选取高度角最高的卫星作为参考卫星r，其余卫星记作卫星s，将伪距观测方程线性化后，通过星间单差（其他卫星和参考卫星作差），可列出B1频率的伪距观测方程，此时接收机钟差可消去，并忽略多路径效应误差，具体公式如下[5]：

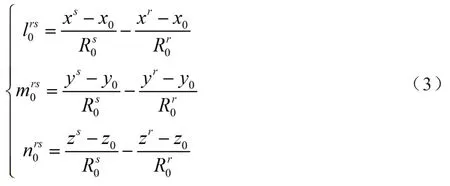
式中：x0、y0、z0为测站点初始坐标，初始坐标可设为(0,0,0)；(xr,yr,zr)为参考卫星r坐标；(xs,ys,zs)为其他卫星s坐标。由于t历元时刻共接收n颗卫星，由式（2）可列出n-1个方程。

同理可列出B2频率的星间单差伪距观测方程，具体公式如下：

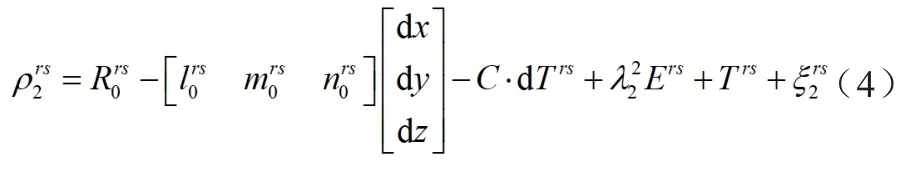
采用不同频率观测值的线性无电离层组合，由于北斗B1频率值为1561.098MHz，B2频率值为1207.14MHz，可写出北斗B1和B2频率的波长比值，具体公式如下：

因此式（2）乘以7632，式（4）乘以-5902，相加后移项可得到如下公式：

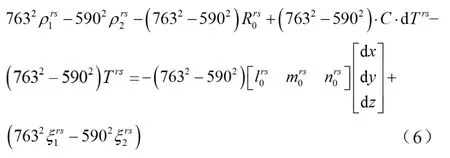
式（6）已消去大部分电离层延迟，方程左边为常数项，其中对流层延迟，可采用Saastamoinen模型进行改正计算，对流层改正模型如下[6]：

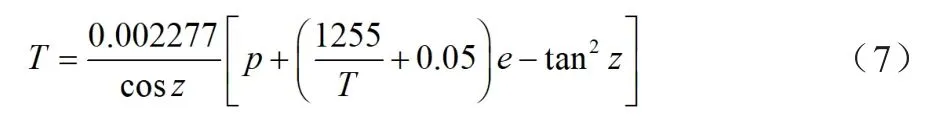
式中：z为卫星天顶距，rad；p为大气压，hPa；T为开氏温度，K；e为水气分压，hPa。

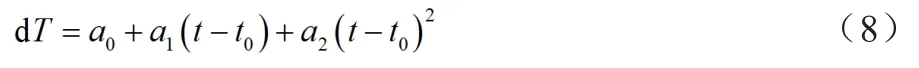
式中：a0、a1、a2分别为卫星钟的钟差、钟速、钟漂。

式（6）可简写为如下公式[8]：

1个历元接收到n颗北斗卫星，可列出n-1个误差方程，式（9）中，常数项矩阵为L(n-1)×1，系数阵为B(n-1)×3，改正数矩阵为V(n-1)×1，未知数矩阵为x3×1。构建误差方程式后，根据最小二乘原理，可计算未知数x，具体公式如下[9]：

由于测站初值设为(0,0,0)，通过式（10）计算得出的x还不是最终结果，需进行迭代运算，因不知道迭代次数，C#程序中可采用while循环语句，循环结束的判别标志可令未知数x＜1cm，根据实测数据验证，一般情况下迭代次数不超过5次即可满足条件。

式（10）的权阵P可通过卫星高度角不同进行定权，高度角越大权值越高。式（6）的观测值为B1和B2频率下的伪距观测值，B1、B2两个频率的伪距值是独立的。观测值组合中误差可设为σ，其取值与卫星高度角有关。观测值方差阵D可用如下公式表示：

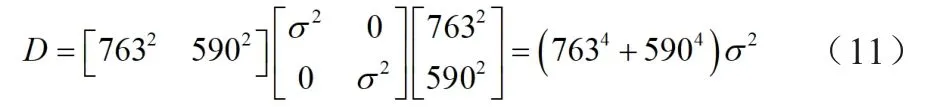
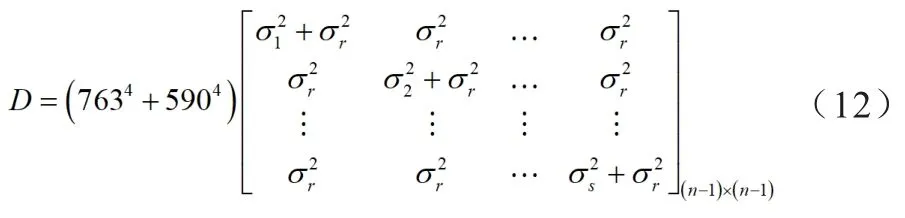
权阵P可通过方差阵D求逆运算得到，代入式（10）可计算未知参数x。

3 BDS和GPS组合单站单历元定位的数学模型

在BDS单卫星系统下单历元单站定位的数学模型中采用星间单差、双频观测值无电离层组合的模式进行计算。若采用BDS和GPS组合卫星系统，则星间单差计算方式有两种，一种是采用GPS和BDS各系统选择自己的参考卫星分开组合星间单差；另一种是仅选择一个参考卫星组混合单差[10]。考虑到组混合单差需要引入系统间偏差，算法较为复杂，故采用第一种计算方式，即BDS和GPS分别各选择系统内的一颗卫星作为参考卫星，按照上述公式进行计算。由于GPS双频观测值（不采用GPS第3个民用频率L5的数据进行计算，因L5观测值目前部分GPS卫星还没有，仅采用L1、L2两个频率）L1频率值为1575.42MHz，L2频率值为1227.60MHz，易得GPS两个频率的波长关系，77λ1=60λ2。将BDS单站定位计算公式中式（6）、式（11）、式（12）中的系数763替换成77，590替换成60，即可得到GPS单站定位的公式。

现将两者组合，设1个历元共接收n颗北斗卫星、m颗GPS卫星的观测数据，可按照上述公式写出组合卫星系统的误差方程式，具体公式如下：

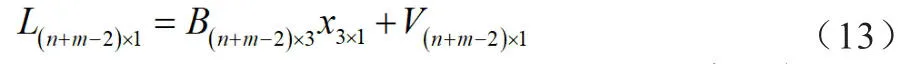
除未知参数x不变外，其余矩阵的行数有所扩充，北斗卫星观测值可列出n-1个方程，GPS卫星观测值可列出m-1个方程，组合形成n+m-2个方程。

此时方差阵D可用分块矩阵表示，具体公式如下：

式中：DBDS为BDS观测值的方差阵，采用式（12）计算；DGPS为GPS观测值的方差阵，将式（12）的北斗双频组合系数换成GPS的组合系数即可；x为未知参数，按式（10）计算。

4 BDS单站多历元定位的数学模型

文章采用单站定位的数学模型未知参数为3个，即测站点的未知数(dx,dy,dz)；而传统单站定位的数学模型未知参数一般有4个，包括接收机钟差。文章通过星间单差（其他卫星和参考卫星观测方程作差）消去了接收机钟差，不将其作为未知参数，由于是静态观测，测站点坐标不会改变，而接收机钟差可能会发生变化，故这里消去了接收机钟差，再利用多历元观测数据计算单站定位的坐标时，便于采用法方程叠加的原理进行计算，具体公式如下：

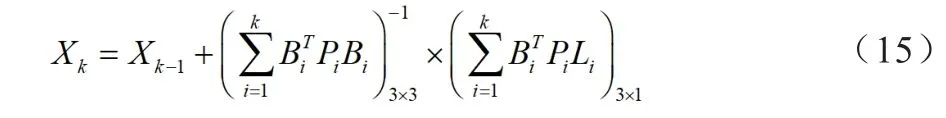
式中：Xk-1为前k-1个历元计算的测站点坐标值；Xk为k个历元计算的测站点坐标值；Bi、Pi、Li分别为第i个历元所形成的系数阵、权阵和常数项矩阵，不同历元观测的北斗卫星数量可能不同，因此各历元的系数阵、权阵、常数项矩阵的行数可能不同。

式（15）是单独BDS多历元单站定位的数学模型，通过单历元GPS和BDS组合卫星系统的单站定位计算模型，易知GPS和BDS组合卫星系统下多历元单站定位的计算公式，亦采用法方程累加的原理，构建的各矩阵由于观测方程的增加而需相应扩充。

当计算出测站点坐标时，精度指标也可同时计算得出。即可通过相应公式计算单位权中误差σ0，求出测站在N、E、U方向的点位精度MN、ME、MU，平面精度因子HDOP值，高程精度因子VDOP值及空间精度因子PDOP值等精度指标。点位精度MN、ME、MU表征计算得到的测站点各方向上的精度，DOP值表征卫星分布的合理性，DOP值与测站和观测卫星构成的单位多面体的体积成反比，DOP值越小，则相应的解算精度越高[8]。

5 实测数据的坐标及精度分析

利用2019年5月在山东菏泽地区某控制点观测约70min的静态数据，采样间隔10s，高度截止角设为15°，共采集357个历元数据。对每个历元进行单站定位计算，只采用BDS观测值，计算得到的测站空间坐标X、Y、Z坐标如图1～图3所示。

由图1～图3可知，单独利用BDS伪距观测值进行单站定位计算，X坐标变化幅度为7.01m，（X最大值为-2291357.8834m，最小值为-2291364.9011m），Y坐标变化幅度为10.21m，（Y最大值为4670024.9080m，最小值为4670014.6962m），Z坐标变化幅度为4.52m（Z最大值为3678370.6212m，最小值为3678366.1014m）。其中Y坐标变化幅度最大，这是因为中国大部分地区Y坐标（空间直角坐标）主要影响高程方向，卫星定位高程方向的精度一般比平面精度低。各历元测站X坐标值大部分落在-2291360～-2291362m，各历元测站Y坐标值大部分落在4670017～4670021m，各历元测站Z坐标值大部分落在3678367～3678369m。结合图1～图3分析，测站定位坐标在第150～180个历元时间段内突变较大，其余时刻测站坐标各分量变化不大。参考RINEX数据O文件给出的测站近似坐标，与BDS各历元计算的单站定位坐标平均值进行较差比较，如表1所示。

由表1可知，O文件提供的近似坐标与利用BDS观测值数据计算各历元单站定位坐标进行比较，坐标差别不大，各分量较差均在1m以下。

现将单独利用BDS和单独利用GPS计算测站各历元单站定位坐标进行较差比较，如图4～图6所示。

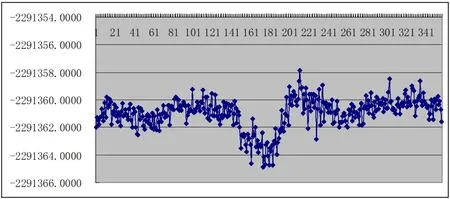
图1 BDS伪距观测值计算每个历元测站点X坐标（单位：m）

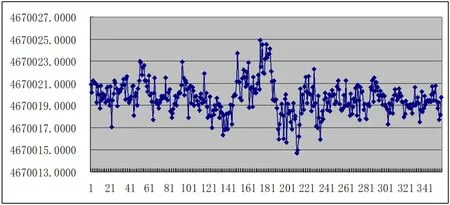
图2 BDS伪距观测值计算每个历元测站点Y坐标（单位：m）

图3 BDS伪距观测值计算每个历元测站点Z坐标（单位：m）

表1 RINEX数据的O文件测站近似坐标 单位：m

由图4～图6可知，单独采用BDS系统和单独采用GPS系统进行单站定位，各历元计算测站点的坐标较差差别不大，大部分历元X坐标较差在2m以下，Y坐标较差在4m以下，Z坐标较差在3m以下。将BDS和GPS各历元单站定位坐标取平均值进行比较，如表2所示。

由表2可知，在分别利用BDS和GPS系统计算各历元单站定位坐标平均值时，分量较差均在2m以下。在BDS系统下单站定位在N、E、U方向的点位精度MN、ME、MU如图7～图9所示。

由图7～图9可知，BDS系统下单站定位精度为米级，大部分历元的E方向的ME和N方向的MN精度值在1.5m以下。该实例数据的E方向点位精度最高，U方向点位精度最低，在第170～180个历元计算U方向的精度最低，MU出现峰值。从图1～图3各历元单站定位计算的坐标各分量X、Y、Z值也可以看出，在第170～180个历元区段内，计算坐标值有明显差异，这与图9历元U方向上的点位精度MU变化特征是相符的。

由于单站定位的精度在米级，文章也只采用了广播星历计算卫星坐标，再按照数学模型进行单站定位计算。从BDS和GPS计算的精度指标结果分析，单独采用BDS和GPS系统进行单站定位精度相当，均能达到米级[11-13]，若采用BDS和GPS混合卫星系统进行单站定位计算，由于广播星历计算的卫星坐标精度约为2m[13]，单站定位精度也只能达到米级，但在个别时段卫星数量较少时进行单站定位解算，此时混合卫星系统下单站定位的解算精度能得到更好的保证。若需要提高定位精度，达到厘米级的定位精度[14]，卫星星历需采用精密星历，观测值需采用载波相位观测值[15]，并准确计算整周模糊度，各种误差分别采用各自的误差改正模型进行改正计算。

图4 BDS和GPS计算各历元测站点X坐标较差（单位：m）

图5 BDS和GPS计算各历元测站点Y坐标较差（单位：m）

图6 BDS和GPS计算各历元测站点Z坐标较差（单位：m）

表2 BDS和GPS各历元单站定位坐标的平均值较差比较表 单位：m

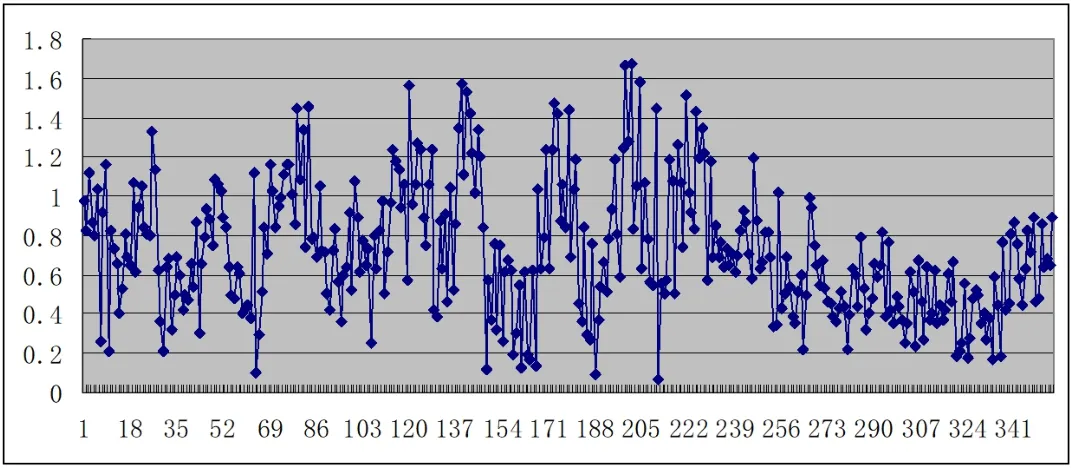
图7 BDS计算各历元单站定位的N方向的点位精度MN（单位：m）

图8 BDS计算各历元单站定位的E方向的点位精度ME（单位：m）

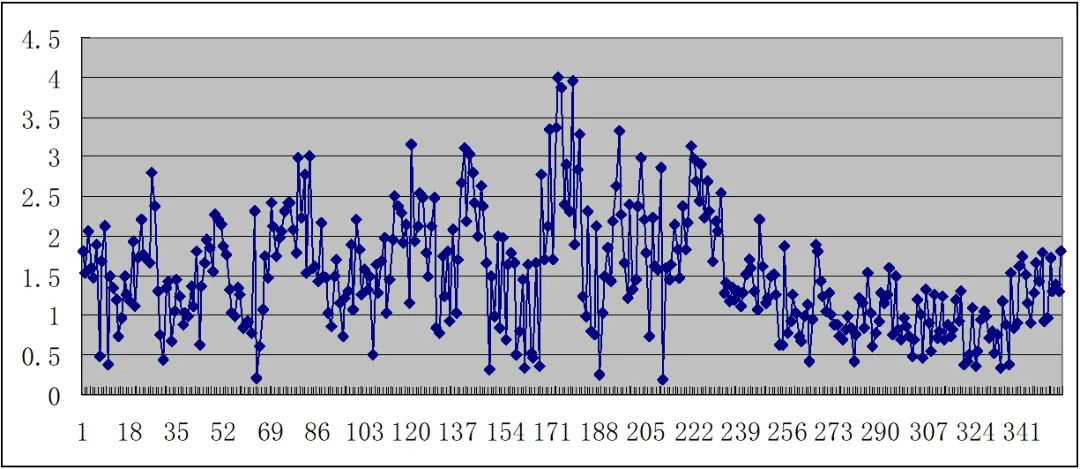
图9 BDS计算各历元单站定位的U方向的点位精度MU（单位：m）

6 结论

文章对BDS利用伪距观测值进行单站定位的数学模型进行了介绍，并通过C#编程实现计算过程。通过实例数据分析，得出以下结论：（1）BDS和GPS单独采用一种卫星系统进行单站定位的精度相当，精度都能达到米级。若采用BDS、GPS混合卫星系统进行单站定位计算，由于广播星历计算卫星坐标的精度约为2m，因此BDS、GPS混合卫星系统下单站定位的坐标精度仍为米级。（2）采用文章的数学模型仅使用BDS进行单站定位计算，将计算结果与RINEX的O文件中提供的近似坐标进行比较，文章实例数据计算的坐标较差在1m以下。BDS单站定位计算的点位精度，平面的点位精度MN、ME高于高程方向的点位精度MU。（3）采用多历元静态观测数据进行单站定位计算时，由于数学模型消去了接收机钟差未知参数，仅保留测站的3个未知参数，在各历元测站点进行静态观测并保持不动，便于采用法方程累加的原理计算多历元单站定位的测站坐标。