基于无网格方法的碳纳米管自由振动分析1)
李 琳 石 峰 项 松 赵为平 王艳冰
*(沈阳广播电视大学数字化资源研发中心,沈阳110003)
†(沈阳航空航天大学,辽宁省通用航空重点实验室,沈阳110136)
碳纳米管是Iijima[1]于1991年发现的。碳纳米管因其优异的电子和机械性能而被广泛应用于纳米电子、纳米器件和复合材料中。许多学者对碳纳米管的自由振动问题进行了研究。Aydogdu[2]利用广义剪切变形梁理论研究了简支多壁碳纳米管的自由振动问题。Yoon等[3]研究了嵌入式多壁碳纳米管的振动问题。Wang等[4]研究了多壁碳纳米管的自由振动。Natsuki等[5]使用 Euler–Bernoulli梁理论分析了双壁碳纳米管的振动特性。Xu等[6]研究了内管和外管之间不同边界条件的双壁碳纳米管的振动问题。Li等[7]研究了基于多壁碳纳米管的纳米机械谐振器的振动特性。Sun等[8]研究了具有初始轴向载荷的多壁碳纳米管的振动问题。Yoon等[9]研究了输送流体碳纳米管的振动和不稳定性。Zhang等[10]研究了在压缩轴向载荷下双壁碳纳米管的横向振动。Wang等[11]通过 Timoshenko梁模型和微分正交方法研究了多壁碳纳米管的振动。He等[12]研究了范德华相互作用模型对多壁碳纳米管振动特性的影响。Hsu等[13]使用Timoshenko梁理论计算了单壁碳纳米管的共振频率。Chang等[14]使用 Timoshenko梁模型研究了包含流体的单壁碳纳米管的自由振动。Lee等[15]使用非局部弹性理论研究了输送流体的单壁碳纳米管的自由横向振动问题。Mir等[16]使用有限元方法研究了单壁碳纳米管的振动特性。连续力学模型主要包括 Bernoulli–Euler梁模型,Timoshenko梁模型和剪切变形梁模型,已被广泛用于研究碳纳米管的自由振动行为。本文采用 Timoshenko梁模型。
碳纳米管振动问题的控制方程是微分方程。求解微分方程的数值方法包括有限差分法,有限元法,有限体积法和边界元法。这些方法均依赖于网格进行局部逼近,但是网格很难生成。无网格法是一种求解偏微分方程的新方法,其中问题域由一组分散的节点进行离散。
无网格法包括无单元 Galerkin方法[17],hp云法[18],再生核粒子法[19],无网格局部Petrov–Galerkin方法[20]和径向基函数配点方法[21-22]。径向基函数主要包括复合二次,逆复合二次,高斯和薄板样条。本文采用薄板样条径向基函数。
本文采用无网格方法来分析碳纳米管的自由振动,薄板样条径向基函数的奇异性通过在零距离处添加无穷小值来消除。将计算结果与参考文献的结果进行了比较。本文的主要目的是证明基于薄板样条径向基函数的无网格方法可以成功地分析碳纳米管的自由振动问题。
1 控制方程和边界条件
考虑一个内径为2R1,外径为2R2,长度为L的双壁碳纳米管,其原理图如图1所示。

图1 双壁碳纳米管的原理图
基于 Timoshenko梁理论的碳纳米管振动控制方程

其中,w为横向挠度,φ为由于梁的弯曲而产生的斜率,I为梁截面的惯性矩,A为梁的截面面积,ρ为梁材料的质量密度,E为梁材料的杨氏模量,G为梁材料的剪切模量,K为剪切因子,ω为梁的圆频率。
固支边界条件

自由边界条件

2 控制方程和边界条件的离散
根据径向基函数法,方程(1)的解近似为

w和φ的导数近似形式为

其中,N为节点总数,和为未知系数,gj为径向基函数,常用的径向基函数有复合二次、逆复合二次、高斯、薄板样条等,径向基函数中形状参数对计算精度影响较大,薄板样条基函数的形状参数选择最容易,因此,本文使用薄板样条径向基函数

其中,rij=xi-xj表示节点i与节点j之间的距离,m为形状参数,本文中m=2。
薄板样条径向基函数在节点间距离为0时存在奇异性。为了消除薄板样条径向基函数的奇异性,当两个节点之间的距离为0时。(其中ς为无穷小值)。
将式(4)~式(7)代入式(1)可得

将式(4)和式(5)代入固支边界条件即可得到

将式(4)和式(5)及其导数代入自由边界条件可得
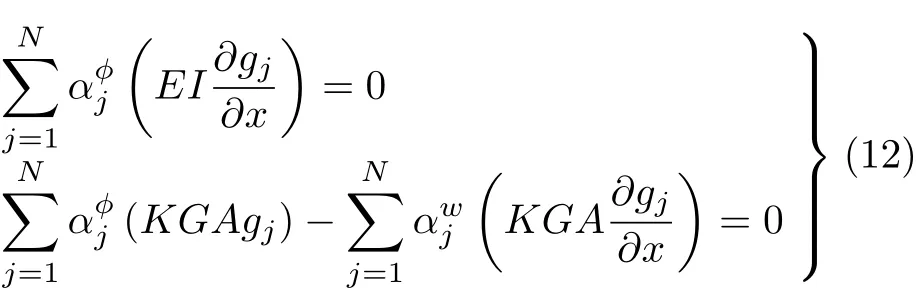
离散化的控制方程和边界条件可以表示为
即

其中,L和 B是微分算子,1/ω2是特征值,α是特征向量。特征值1/ω2可以用标准的特征值求解器求解。
3 数值算例
双壁碳纳米管的几何参数和材料属性:2R1=0.7 nm,d=2R2=1.4 nm。
单壁碳纳米管的厚度t=0.35 nm,弹性模量E=1 TPa,剪切模量G=0.4 TPa,泊松比v=0.25,密度ρ=2300 kg/m3。A=A1+A2,I=I1+I2,其中1和2分别表示内管和外管的数量。剪切系数K为

其中,α=(2R1-t)/(2R2+t)。
采用均匀节点模式对纳米管进行离散(图2),第i个节点的坐标为

其中,N为节点总数。内部节点由控制方程控制,端点由边界条件控制。

图2 双壁碳纳米管的节点分布
无量纲固有频率

3.1 收敛性研究
为了检验本文方法的收敛性,考虑了L/d=10两端固支的双壁碳纳米管。图3和图4为两端固支双壁碳纳米管的无量纲前两阶固有频率,其节点分布从11增加到101。

图3 当L/d=10时,两端固支双壁碳纳米管无量纲一阶频率的收敛性研究

图4 当L/d=10时,两端固支双壁碳纳米管无量纲二阶频率的收敛性研究
结果表明,基于薄板样条径向基函数的无网格方法计算的结果与文献[11]的结果具有较好的一致性,随着节点数增加,计算结果逐渐趋近于Wang[11]的结果。
3.2 比较研究
为了验证本文的薄板样条径向基函数法在求解双壁碳纳米管自由振动问题中的数值精度,进行了比较研究。在比较研究中,节点数为101。
表1列出了不同长径比的两端固支碳纳米管的无量纲前10阶频率,表 2列出了不同长径比的固支-自由碳纳米管的无量纲前10阶频率。由表1和表2可知,本文结果与文献[11]的结果具有很好的一致性。

表1 两端固支双壁碳纳米管的无量纲前10阶频率(N=101)

表2 固支-自由双壁碳纳米管的无量纲前10阶频率(N=101)
4 结论
本文提出了一种基于薄板样条径向基函数的无网格方法来分析双壁碳纳米管的自由振动问题。收敛研究和比较研究分别用于检验本方法的收敛性和数值精度。数值算例表明:随着长径比增加,各阶固有频率逐渐增加;薄板样条径向基函数可以准确地用于分析双壁碳纳米管的自由振动问题。

