温湿度检定仪中的数字式仪表识别

祝长生, 张成元, 徐亚超

(山东科技大学智能装备学院，泰安 271019)

计量是国民经济的一项重要技术基础，数字式温湿度计的计量检定是计量工作中的一项重要内容。目前，很多温湿度检定仪还没有计算机接口，需要人工读取仪表示数，做出检定结果。为了实现这类仪器的自动化监测，需要加装机器视觉设备，通过工业相机定时拍摄仪表数字显示区域，利用计算机进行图像采集和处理识别，实现仪表示数的自动读取，进而比较表盘示数与实际温湿度的误差，判定被检定仪表是否合格。在此过程中，数字式仪表示数的图像处理与识别算法是温湿度检定仪实现自动化监测的关键所在。数字式仪表示数读取主要包括数字分割和数字识别两个部分，其中数字识别的研究是最为关键的步骤。

目前，中外的研究人员已经提出了一些有较高实用价值的数字识别算法，如王荣本等[1]为了满足自动导引车(automated guided vehicle，AGV)对数字准确、快速识别的要求，提出了基于反向传播(back propagation，BP)神经网络的数字识别方法，该方法具有良好的自学习能力，但是需要大量的数据进行训练；宋晓茹等[2]提出了基于深度神经网络模型的手写体图像识别方法，让机器自动学习特征，通过改进成本函数，提高了手写数字识别的识别率，但深度学习算法对硬件配置要求较高；张艰等[3]利用水平和垂直投影方法对分时电表表盘数字实现了精确定位分割，但是该方法对拍摄的光照及亮度有较高的要求，容易受噪声影响；张艳玲等[4]利用不变矩特征实现了仪表盘参数符号的识别，识别的准确率高达98.87%，但是该方法要求图像亮度不能低于30，一次识别的仪表符号不能太多[4]；王明俊等[5]基于数字结构特征建立了数字的Fisher线性判别模型，在内部测试数据集上取得了非常不错的识别率；Edward[6]采用支持向量机(support vector machine，SVM)算法实现了对电力仪表示数的自动识别；陈蔼祥[7]对SVM等6种分类器的性能进行了测试与评估，实验证明SVM具有更好的泛化能力。

现提出一种基于不变矩信息融合的数字式仪表示数识别方法。通过提取数字图像的Hu矩和Zernike矩等特征，然后将两者通过特征融合构成特征向量，训练SVM分类器，得出各不变矩与目标类别之间的关系，从而实现对数字的识别。

1 仪表盘图像预处理

高质量的图像是数字精确分割与识别的重要保障。对工业相机采集到的图像进行预处理包括图像滤波、图像增强、图像校正、图像分割与骨骼细化等。

1.1 图像滤波

图1为系统相机原始采集图像，效果相对理想。为了保证算法的鲁棒性，在原采集图像的基础上混叠了期望值为0、标准差为0.1的高斯白噪声，泊松噪声以及标准差为0.1的斑点噪声，加噪后的图像如图2所示。

为了滤除图像中存在的噪声干扰，保证图像的平滑并使图像轮廓保持清晰，分别对加噪图像进行了高斯滤波、双边滤波、中值滤波、非局部均值滤波(non local means, NLM)，如图3所示，通过比较各种滤波方法的滤波效果，发现NLM算法的图像信噪比最高(表1)，明显优于其他四种基本滤波方法，所以最终选用了NLM算法。

图1 原始图像Fig.1 Original image

图2 加噪图像Fig.2 Noised image

图3 滤波算法效果对比Fig.3 Comparison of filtering algorithms

表1 滤波后图像信噪比

1.2 图像增强与图像分割

观察原始图像可以发现，由于光源因素和液晶屏的反光特点，图像中的数显部分对比度不够高，需要采用图像增强技术改善数显部分的对比度。通过分析直方图均衡法、拉普拉斯算子法、伽马变换法等算法，并观察这三种图像增强算法的效果(图4)，直方图均衡化对图像进行了全局无差别对比度增强操作，拉普拉斯算子边缘锐化的效果比较明显，但是这两种方法对图像的局部亮度差都没有明显的改善，所以不能满足需求。而经过伽马变换法处理的图像亮、暗区域的灰度得到了不同程度的拉伸和压缩，图像整体变亮。

对增强后的图像采用最大类间方差法进行阈值分割，分割后再进行图像二值化，效果如图4所示。显然伽马变换法增强后的阈值分割效果最好，因此，选择伽马变换法作为图像增强算法。

图4 图像增强和二值化比较Fig.4 Comparison of image enhancement & binarization

1.3 图像校正

图像的采集过程中，仪器的摆放不可避免地会出现一定程度的倾斜，给字符分割和特征提取带来很大困难，影响仪表示数的识别精度。观察图像特点，实验以矩形的长直边作为基准线，通过Hough变换进行直线检测，并运用最小二乘法拟合成直线，最后通过直线方程的斜率校正图像。

Hough变换是一种通过坐标系变换，并运用投票原理检测直线和有规律的曲线等特定形状对象的算法[8-9]。Hough变换通过将二维空间中，经过像素点p(x0,y0)的一簇直线[式(1)]从笛卡尔坐标系转换到极坐标系[式(2)]，如图5所示。对于一般像素点(x0,y0)，通过此点的一系列直线可统一定义[式(3)]，那么每对(r,θ)都可以代表一条经过点(x0,y0)的直线，如图6所示。通过找到在平面θ-r中相交于同一点的曲线，可以检测到笛卡尔坐标系中的直线。

y0=mx0+b

(1)

r=xcosθ+ysinθ

(2)

rθ=x0cosθ+y0sinθ

(3)

式中：m为斜率；b为截距；r为极径；θ为极角。

实验选择最长的线段作为基准线(浅黄色标出)，以基准线的斜率为尺度旋转校正图像，校正后的图像如图7所示。

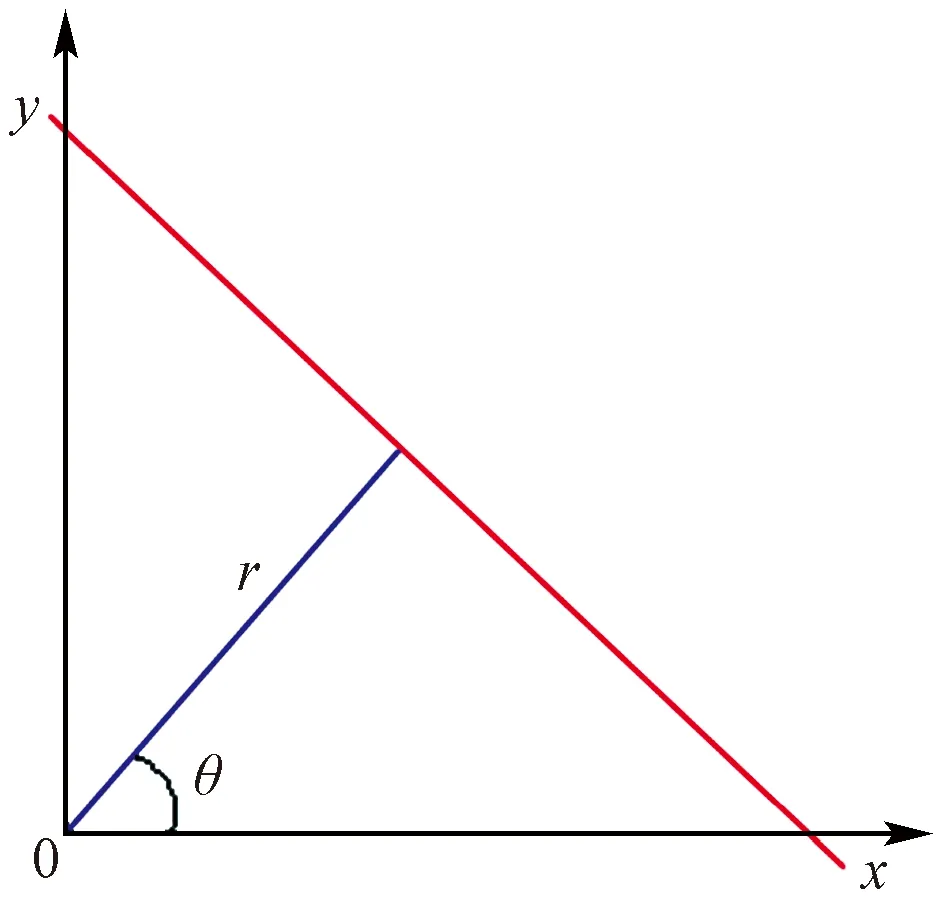
图5 笛卡尔坐标系下的直线Fig.5 Linear diagram in Descartes coordinate system

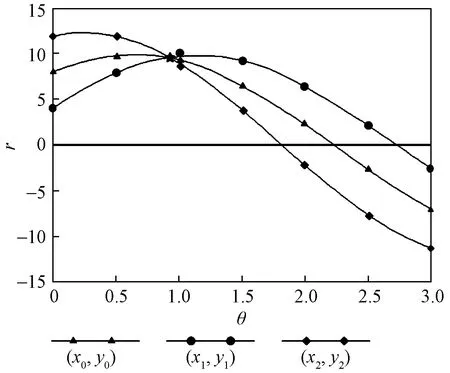
图6 直线上三个像素点映射到极坐标系Fig.6 Three pixel on the line mapping to polar coordinate system

图7 仪表图像校正结果Fig.7 Image rectification

2 图像截取与骨骼细化

图像中只有数字以及数字的位置是有价值的信息，为了消除不必要的干扰因素，首先用Two-Pass算法对二值图像进行连通域扫描，精确定位数字区域并逐个截取。然后采用非端点位置像素置零的连通域骨骼细化方法对数字图像进行迭代，具体迭代方法如下。

第一步选出满足下列条件的点：八邻域中黑点的数目大于等于2且小于等于6；将所有邻接点之间按序前后分别成对值为0、1的个数等于1；上下右邻接点之积等于0；左右下临界点之积等于0。如果同时满足以上四个条件则该点可以置为0。

第二步选出满足下列条件的点：八邻域中黑点的数目大于等于2且小于等于6；将所有邻接点之间按序前后分别成对值为0、1的个数等于1；上左右邻接点之积等于0；上下右临界点之积等于0。如果同时满足以上四个条件则该点可以置为0。这样反复迭代，直到获取细化图像为止。图像细化效果示意如图8所示。最后将细化后的图像采用等比例缩放的方法归一化为32×16尺寸。

图8 图像细化Fig.8 Image thinning

3 仪表数字识别

截取到准确的数字区域并细化之后，问题就转换为对数字的识别，Hu矩和Zernike矩是最常应用于图像识别的不变矩。

3.1 Hu矩

设f(x,y)为二维连续函数，其(p+q)阶原点矩和中心矩定义为

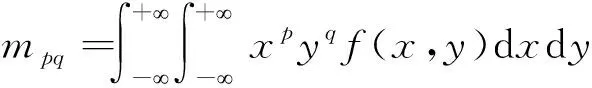
(4)

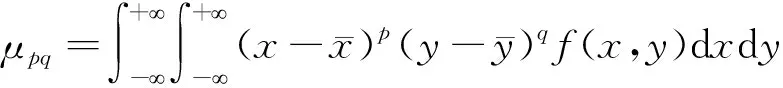
(5)

在数字图像g(x,y)中，原点矩和中心矩可以写为

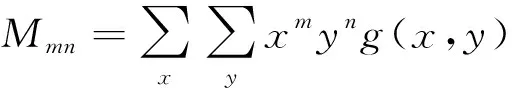
(6)

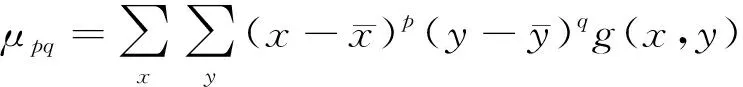
(7)

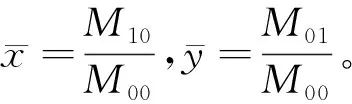
中心矩具有平移不变性，原点矩具有尺度不变性，平移和尺度不变量ηij通过适当的缩放零阶中心矩来构建。

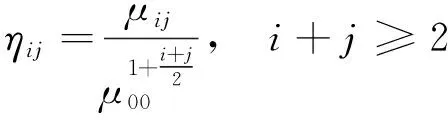
(8)

Hu矩利用二阶和三阶中心矩构造了7个不变矩，但是7个不变矩的变化比较大，还有出现负值的可能，所以实际实验中采用的是各不变矩绝对值的对数。

3.2 Zernike矩

Zernike矩是基于Zernike多项式的正交化函数，具有图像旋转不变性，可以构造任意高阶矩。其数学表达式[10]为

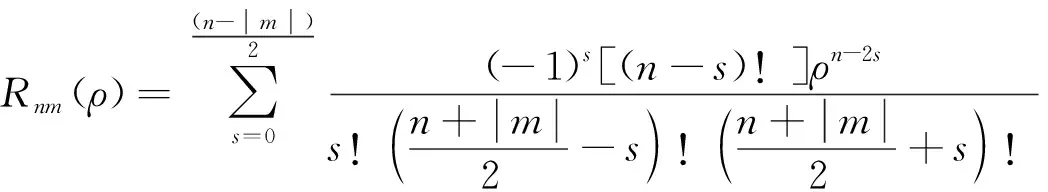
(9)

Vnm(x,y)=Vnm(ρ,θ)=Rnm(ρ)ejmθ

(10)

式中：Rnm(ρ)为点(x,y)的径向多项式；Vnm(x,y)为Zernike正交多项式；n、m为Zernike正交多项式的阶数；n为非负整数，n-|m|为偶数，并且n≥|m|。研究者在Zernike正交多项式的基础上给出了二维函数f(x,y)的Zernike矩定义为

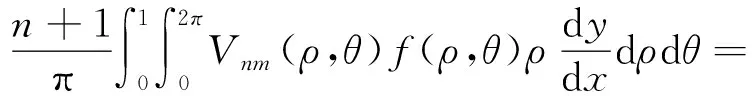
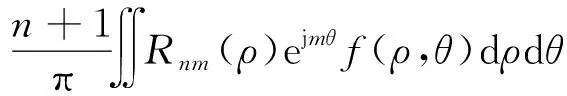
(11)

对于二维数字图像，Zernike矩为复数，将它的实部和虚部分别记为Cnm和Snm，则有

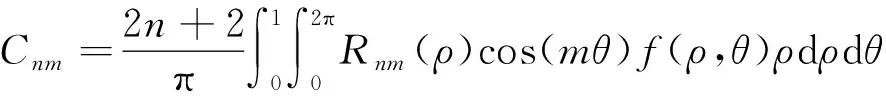
(12)

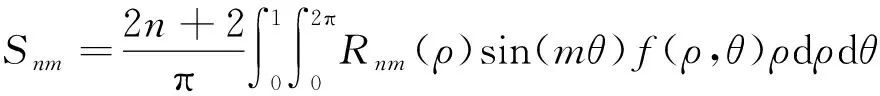
(13)

极坐标下的Zernike矩定义为

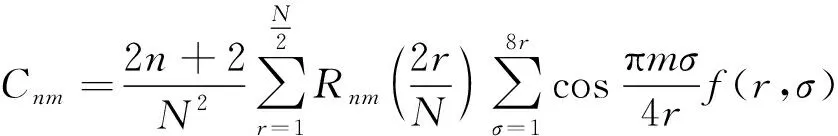
(14)

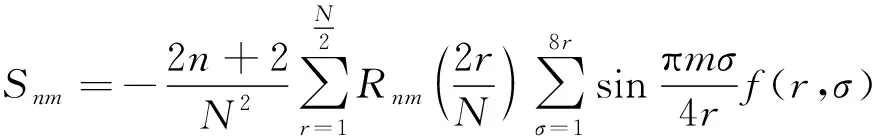
(15)

由此提出Zernike矩的计算方法：首先确定图像函数f(x,y)的N×N大小，从而确定Cnm和Snm计算公式中的N，进一步可以确定r和σ的范围；然后利用Zernike多项式的快速递推性质计算各阶Rnm，计算出Cnm和Snm，最后对Cnm和Snm求模，进而得出|Znm|，作为图像识别的特征依据。

4 实验仿真与方案验证

不变矩用于图像识别时，通常使用直观对比的方法，如单一不变矩的直接比对，或多阶不变矩的最小距离法，此种方法模型简单，但误差率较大。SVM是传统统计学习的分类算法中效果最好的，且有严格的数学推理过程。BP神经网络是典型的黑箱模型，具有强大的自学习逼近能力。基于不变矩信息融合的数字识别方法，就是使用合适的算法融合目标图像的不同种、不同阶的不变矩特征，通过训练得到优秀的数学模型，进而实现对目标图像的识别。

4.1 硬件平台

实验以MATLAB为仿真平台，实验所用的计算机操作系统为Windows 7，英特尔酷睿i7处理器、英伟达GeForce 960显卡、8 G内存条。

4.2 数据预处理

实验共采集到1 793个数字图像，分别采用模板匹配法、像素位置权重法、深度学习法、基于不变矩信息融合法进行了算法评估比较。首先，根据前述方法对图像进行预处理[11](模板匹配法不进行骨骼细化处理)。其次，针对深度学习算法，采用VGG16网络模型，对截取的图像进行尺度变换，统一为224×224(尺度变换方法采用类似卷积神经网络中的池化层操作)；最后，对计算得到的不变矩数据进行归一化处理，结果映射到[0，1]之间，转换函数为

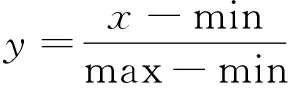
(16)

对于后两种需要训练的模型，将所有图像(基于不变矩信息融合法为该图像的不变矩计算结果)划分为训练集、验证集和测试集。

(1)训练集：作用是模型估计，即学习样本数据集，通过匹配一些参数来建立一个分类器。这里选择897个图像作为训练集。

(2)验证集：对学习出来的模型，调整分类器的参数，例如在神经网络中选择隐藏单元数，验证集还用来确定网络结构或者控制模型复杂程度的参数。选择448个图像作为验证集。

(3)测试集：检验最终学习到的模型性能如何，主要是测试训练好的模型的分辨能力(识别率等)。选择448个图像作为测试集。

4.3 实验仿真结果

将参与评估算法的预处理以及训练所使用的总时间、识别时间和识别正确率进行统计：传统方法与深度学习的实验结果在表2，表3是使用不同分类器以及使用不同不变矩作为输入数据进行实验的结果。根据前人经验，Hu矩使用低阶矩的识别效果较好，表3是选取Hu矩中的φ1、φ2、|Z00|、|Z11|及Zernike矩中的|Z00|和|Z11|作为输入特征得出的结果。

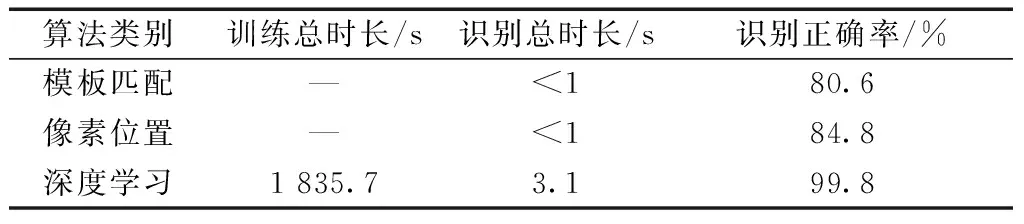
表2 传统方法与深度学习的实验结果

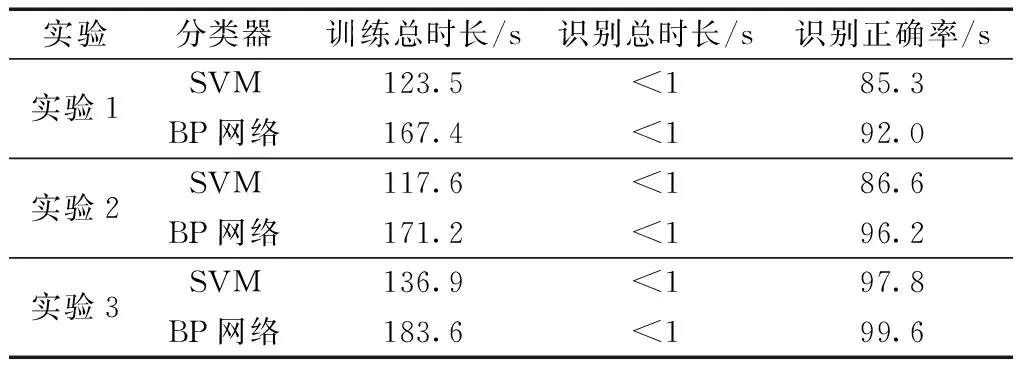
表3 基于不变矩信息融合方法的实验结果

由表3的实验数据可以分析得出，传统方法的识别速度最快，但是识别的准确率太低，无法作为满足需求的识别算法；深度学习可以满足识别精度的要求，但是其无论是训练和识别都用时过长，对系统的要求较高；基于不变矩信息融合的方法与传统方法在识别时间上相差较小，且当BP神经网络作为信息融合方法，选取φ1、φ2、|Z00|、|Z11|四个不变矩同时作为输入时(这里的隐含层设置为两层12节点，输出层节点数为10)，该方法与深度学习在识别精度上也只有不超过0.2%的差距。所以综合考虑，基于取φ1、φ2、|Z00|、|Z11|四个不变矩特征，并选用BP神经网络分类器作为信息融合方法的识别方案符合要求。

4.4 方案验证

实验仍沿用上述PC硬件，采用Basler公司acA1600-60gc型号CMOS相机，BP-FA-0601C型号镜头，加偏振镜，LTS-2BRS40030-W型长度为400 mm白色条形面光，LTS-APC2460-2型光控制器，以Visual Studio 2017为开发平台，以C++语言配合OpenCV开源视觉库中的相关算法函数进行了实现和应用开发。

实验过程中，将待检仪表放入NM-HWS01温湿度检定仪中，将检定仪设置成10 ℃+30%RH(RH为相对湿度)、20 ℃+50%RH和30 ℃+70%RH三种温湿度参数，每隔30 min设置一次，每次待箱内温湿度环境稳定，采集50个待检测仪表图像，将数据上传至上位机进行图像处理识别，同时由记录下人工观测结果作为实际读数。

待检仪表的温度单位刻度为1 ℃，湿度单位刻度为2%RH，故按检定要求温度合格阈值是±0.5 ℃，湿度合格阈值是±1%RH。实验结果如表4所示。

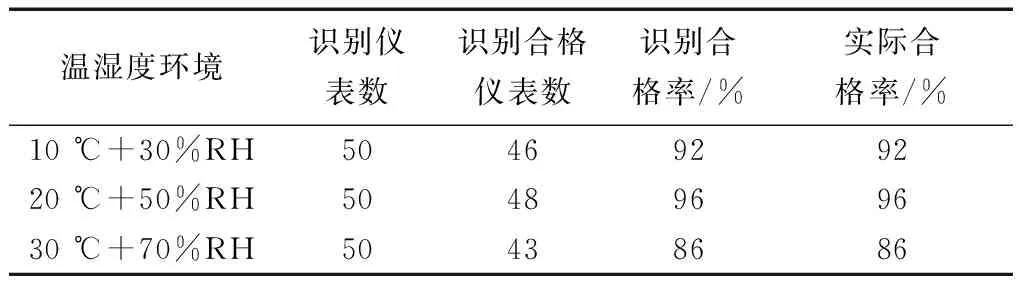
表4 实验结果

通过对实验数据分析可知，识别合格率与实际合格率相符。因此，提出的基于机器视觉的数字式仪表读数识别系统在此项目的实际应用中，具备可行性和高精确度。

5 结论

提出了一种基于不变矩信息融合的数字式仪表示值识别算法，对数字识别问题提出了新的理论思路，极大地降低了模型的复杂度，提高了检测效率。同时利用现场实际采集的仪表图像对该算法进行了验证。实验结果表明，该算法具有很高的精确性和可行性，能够满足项目要求。由于提出的识别算法对仪表类型的针对性较强，条件约束比较明显，所以实际应用中也存在一定局限性。虽然经过图像的预处理和算法的不断优化消除了很多干扰因素，但后续若进行环境更为复杂的识别实验，准确率降低是可以预见的。