基于动态燃料成本双层优化的燃煤发电企业管控模型

廖志伟 张文锦 陈琳韬 黄杰栋 庄竞

摘   要：为使燃煤发电企业降低燃料成本，实现燃料科学管控，提出一种综合考虑发电可靠性和生产经济性的燃料成本双层优化模型，上层为电煤采购库存混合整数规划模型，下层为混煤掺烧非线性优化模型，双层模型交替迭代协调优化，实现燃料管控动态决策. 针对优化模型高维多约束情况，提出一种混沌映射初始化和高斯变异结合的改进灰狼优化算法. 以某燃煤电厂模拟运营进行算例验证分析，结果表明，所提模型可以降低燃煤电厂7.80%的燃煤成本，证明了所提模型与求解算法的有效性和可行性.

关键词：燃煤电厂;动态规划;电煤采购;混煤掺烧;灰狼优化算法

中图分类号：TM621                             文献标志码：A

Management and Control Model of Coal-fired Power Generation

Enterprise Based on Dynamic Fuel Cost Bi-level Optimization

LIAO Zhiwei†，ZHANG Wenjin，CHEN Lintao，HUANG Jiedong，ZHAUNG Jing

（School of Electric Power Engineering，South China University of Technology，Guangzhou 510641，China）

Abstract：In order to reduce fuel costs and achieve scientific fuel control in coal-fired power generation enterprises， a bi-level fuel cost optimization model that comprehensively considers the reliability of power generation and the economy of production is proposed in this paper. The upper layer is a mixed integer programming model for power coal purchasing and inventory， while the lower layer is a nonlinear optimization model for mixed coal combustion. The bi-level model is the alternating iterative coordination optimization to realize the dynamic decision-making of fuel control. Then， an improved gray wolf optimization algorithm combining chaos mapping initialization and Gaussian mutation is proposed for the high dimensional and multiple constraints of the optimization model. Finally， a simulated operation of a coal-fired power plant is used to verify the results. The results show that the proposed model can reduce the coal cost of coal fired power plant by 7.80%， which proves the effectiveness and feasibility of the proposed model and solution algorithm.

Key words：coal fired power plants;dynamic programming;electric coal purchase;mixed coal blending;grey wolf optimization algorithm

隨着电煤价格双轨制取消以及供给侧结构性改革引起电煤市场波动性增强，电煤价格连年走高[1]，直接导致燃煤发电企业生产成本提高;与此同时，风电、光电等低边际成本可再生能源参与电力市场竞争，导致市场出清价格接近或低于燃煤机组发电成本，并使得燃煤电厂中标发电量进一步降低[2]. 以燃煤电厂为代表的传统火电企业陷入电力市场运营困境，甚至出现亏损情况[3]. 因此，火电企业亟须优化现行运营策略以降低发电成本从而增强电力市场竞争力.

燃煤电厂的燃料成本占据发电成本的70%～80%，分别受电煤采购入厂环节、电煤库存管理环节及电煤入炉掺烧环节影响[4]，国内外不少学者对燃煤电厂燃料管控策略展开研究. 文献[5-7]将电厂电煤库存管理与电煤采购决策相联系，对电煤库存管理问题建立混合整数线性规划模型，在不同煤炭供应商中选择最优采购组合方案. 文献[8-9]讨论不同风险类型电厂决策者考虑现货价格波动情况下的不同燃煤采购策略，在不同煤炭供应商中求解最优采购组合方案. 文献[10]结合动力煤期货和现货市场，优化电厂库存策略，减少电煤库存对电厂流动资金的占用. 文献[11]以电厂年度收益条件风险价值最小为目标，考虑煤价和上网电价不确定性，运用线性规划对电厂燃煤库存优化模型求解. 然而，上述文献研究燃煤电厂库存管理策略和采购方案是基于电煤发电消耗固定的前提，根据电煤价格波动，尽可能选择购买低价煤，忽视电厂内锅炉混煤掺烧比例对发电燃料成本的影响. 为此，也有不少学者研究锅炉最佳混煤掺烧方案. 文献[12]通过调整混煤掺烧方案使其燃烧特性接近锅炉设计目标煤质，并优化煤场库存存放位置减少入炉混煤调运时间. 文献[13-15]研究不同混煤掺烧方案下对锅炉气体排放和碳化合物排放的影响，优化锅炉燃烧对环境污染的排放. 文献[16]建立入炉混煤标准煤单价价差模型计算燃煤电厂燃料成本，证明直接掺烧便宜劣煤不能有效降低燃煤成本. 文献[17-18]兼顾燃煤电厂锅炉运行的安全性和经济性，通过掺烧试验得出保证锅炉安全运行下经济性较好的混煤掺烧方案.

综上可知，传统火力电厂由于信息系统孤岛及燃料部门和采购部门对发电可靠性和生产经济性的侧重点不同，混煤掺烧方案难以与电煤采购方案实现协同全局优化燃料管控.

随着计算机、数字化和大数据技术的发展，使燃料管控整体动态全局寻优成为可能，本文提出一种综合考虑发电可靠性和生产经济性的燃料成本双层优化模型，通过多个环节动态耦合，将部分环节局部静态优化转换成全局动态优化燃料管控方案. 首先，梳理燃煤电厂传统燃料管控流程工作逻辑，分析燃料管控对发电成本的影响;其次，分别构建上层电煤采购库存混合整数规划模型和下层锅炉混煤掺烧非线性优化模型，其中，上层模型以采购成本和库存成本最低为目标函数，确定采购方案，向下层模型传递可用电煤;下层模型以锅炉燃烧混煤平均标准煤单价最低为优化目标，确定掺烧方案，并向上层模型传递电煤需求计划. 然后，将上下层模型交替迭代协调优化，并使用混沌映射初始化和高斯变异结合的改进灰狼优化算法求解燃料成本双层优化模型;最后，以某燃煤电厂为算例验证双层优化模型的可行性.

1   燃煤电厂运营机制及双层优化模型

1.1   燃煤电厂运营机制成本模型

燃煤电厂的燃料成本与其燃料管控水平息息相关，电煤从采购到生产的全过程如图1所示.

影响燃料成本的过程主要为厂外采购环节、电煤库存管理环节和锅炉混煤掺烧环节. 在不同的环节，发电燃料成本有不同的表现形式，为方便本文描述，做如下定义：

入厂原煤单价pi，m，反映电厂采购水平：

pi，m =             （1）

入炉标准煤单价p*

j，m，体现库存管理水平：

p*

j，m={+}

（2）

入炉混煤标准煤单价p*

m，决定发电燃料成本：

p*

m = εj，m p*

j，m         （3）

式中：pi，m为第m周第i种电煤入厂原煤单价;pc

i，m为港口煤单价;pt

m为入厂运费单价;ph

m为入厂印花税; pz

m为入厂杂散费;ηm为运输损耗;p*

j，m为第m周第j类电煤的入炉标准煤单价;Pj，m为当周该类煤采购量;Sj，m-1为上周该类煤囤积量;φ为电煤库存管理费用单价;θ为电煤囤积导致的资金积压利息月利率; Q*

net、Qnet，j分别代表标准煤和对应电煤低位发热量; Nj为燃煤电厂库存电煤分类种数;p*

m为第m周混煤入炉标准煤单价;εj，m为第j类电煤在第m周的掺烧比例.

1.2   燃料成本双层优化模型

由1.1節可知，采购环节与库存管理直接相关，本文针对对应环节分别建立电煤采购库存模型和混煤掺烧优化模型. 考虑到采购环节和配煤环节是相互影响、相互制约的关系，将二者构建为如图2所示的燃料成本双层优化模型.

上层电煤采购库存模型中，以电煤采购总成本最低为目标函数，采购周期内各类电煤采购量作为决策变量，考虑电厂库存和煤炭供应满足最小发电计划需求从而保证发电可靠性，求解采购库存方案并向下层混煤掺烧优化模型传递电煤入厂标准煤单价和可用电煤.

下层混煤掺烧优化模型中，以入炉混煤平均标准煤单价最低为目标函数，决策变量为各类电煤掺烧比例，约束条件以供热约束、库存约束和锅炉约束的形式保证锅炉燃烧生产的可靠性，通过求解混煤掺烧方案向上层优化模型传递电煤消耗情况.

通过迭代上下层模型协同优化目标函数，避免单独求解模型时陷入燃料成本局部最优情况，探寻全局最优燃料管控方案.

1.2.1   电煤采购库存模型

1）目标函数. 本文在文献[4]基础上将电煤采购总成本C分为厂外购入成本C1和厂内仓储成本C2，厂外购入成本C1集中体现为入厂原煤单价和电煤采购量，厂内仓储成本C2包括电煤库存管理费用和采购资金积压利息：

min C = C1 + C2           （4）

C1 = xi，m Ui pi，m         （5）

C2 = （xi，m Ui φ + yi，m pi，m θ）         （6）

式中：Nm为采购周期内周数;Ns为可选电煤供应商数;整数型决策变量xi，m代表电厂第m周向第i个煤炭供应商的购买批次;Ui代表向第i个煤炭供应商单一批次电煤购买量;yi，m为跨月提前采购电煤数量.

2）约束条件分为供货约束，电厂库存约束，分类库存约束.

①供货约束. 根据有无月前预订合同，燃煤电厂向电煤供应商订购的动力煤可分为长协煤和现货煤. 长协煤单月采购量应在合同的预定范围内，对应供货约束如下：

Smin，i≤xi，m Ui ≤Smax，i       （7）

式中：xi，m Ui 代表电厂向第i个煤炭供应商单月采购的电煤量;Smin，i和Smax，i分别为煤炭供应商在合同中签订的最低采购量和最高采购量.

②电厂库存约束. 由于电厂存放煤炭场地有限，同时要保证最小连续发电天数，电煤库存数量介于电厂库存上下限之间，即

Pm =xi，m Ui         （8）

St

m = St

m-1 + Pm - Ct

m       （9）

St

min ≤ St

m ≤ St

max       （10）

式中：Pm为电厂第m周的电煤采购总量;Ct

m为电厂第m周的电煤消耗总量;St

m为电厂第m周的电煤库存总量，由式（8）（9）计算得到;St

min和St

max分别为电厂总库存下限和上限.

③分类库存约束. 为保证电厂生产安全连续进行，各类电煤库存数量应保持在安全范围内，即

Pj，m = xi，m Ui        （11）

Sc

j，m = Sc

j，m-1+ Pj，m - Cc

j，m      （12）

Sc

min≤ Sc

j，m≤ Sc

max       （13）

式中：Cc

j，m为电厂第m周第j类电煤的消耗量;Sc

j，m为第m周第j类电煤的库存量，由式（11）（12）计算得到;Sc

min和Sc

max分别代表电厂分类库存下限和上限.

1.2.2   混煤掺烧优化模型

1）目标函数. 当发电计划确定时，机组发电所需的标准煤耗量确定，发电成本取决于入炉混煤平均标准煤单价，因此混煤掺烧优化模型以最低入炉混煤平均标准煤单价为目标函数[16]：

min p*

m = εj，m p*

j，m         （14）

2）約束条件分为供热约束，库存约束，锅炉约束.

①供热约束. 锅炉燃烧提供的热量须满足根据反平衡法计算机组发电的热量需求，即

Qnet，m =εj，m Qnet，j         （15）

Ct*

m = Gm gm /（1 - ηg）       （16）

Ct

mQnet，m ηQ ≥Ct*

mQ*

net           （17）

式中：Qnet，m为混煤平均低位发热量，满足混煤掺烧线性可加性;Ct*

m为第m周的发电标准煤耗量;Gm为第m周的发电量;gm为第m周的机组发电单位标准煤耗量;ηg为厂用电率;ηQ为锅炉热效率，受混煤低位发热量影响，由混煤试烧试验得出.

②库存约束. 机组发电使用电煤耗量受电厂当周可用电煤限制，即

0≤Ct

m≤St

m-1+Pm         （18）

Cc

j，m= Ct

mεj，m         （19）

0≤Cc

j，m≤Sc

j，m-1+ Pj，m         （20）

③锅炉约束. 为保证锅炉安全生产，混煤煤质应在锅炉燃烧设计范围内，具体如下：

Qnet，min≤Qnet，m ≤Qnet，max       （21）

Sm = εj，m Sj         （22）

Sm≤Smax       （23）

Vdaf，m = εj，m Vdaf，j         （24）

Vdaf，min≤Vdaf，m≤Vdaf，max        （25）

Tamp，min≤Tamp，m≤Tamp，max        （26）

式中：Sm和Vdaf，m分别为第m周的混煤全硫分和混煤干燥无灰基挥发份，均满足混煤掺烧煤质线性可加性;Tamp，m为第m周的混煤灰熔点温度，由混煤试烧试验得出.

2   灰狼优化算法

灰狼优化算法 （Grey Wolf Optimizer，GWO） 是Mirjalili等[19]在2014年受野外狼群的等级机制和狩猎方式启迪而提出的群体智能优化算法，在低维寻优问题中表现出较好的搜索能力和收敛速度，对混煤掺烧非凸优化模型求解有不错的适应性和鲁棒性，但是面对电煤采购库存模型中高维的可行解空间和复杂时空连续性约束情况，GWO算法出现种群个体质量低和早熟收敛问题. 为此，本文从种群初始化和个体变异两方面出发，分别使用混沌映射种群初始化算子和高斯变异算子改进灰狼优化算法（Improved Grey Wolf Optimizer，IGWO）.

2.1   改进灰狼优化算法

2.1.1   混沌映射种群初始化算子

电煤采购库存模型的求解质量依赖于种群初始化的采购库存方案分布情况，优秀的初始化种群采购库存方案尽可能在可行解空间呈现多样化，对算法的全局搜索能力和收敛速度都有不错的提升. 相较于计算机伪随机数生成，非线性的混沌映射具有初值敏感性和空间遍历性的特点，可以提高初始化方案的多样性.

本文采用Tent映射产生[0，1]随机混沌序列，再通过等比放大映射为初始化电煤采购库存方案种群，Tent映射的表达式如下：

zk+1 = zk/β，zk∈（0，β]

（1 - zk）/（1 - β），zk∈（β，1]      （27）

Xi，m = round（Xmin

i，m + zk（Xmax

i，m - Xmin

i，m））    （28）

式中：zk为初始随机数;β为混沌因子控制参数，取β = 0.3;Xmin

i，m、Xmax

i，m分别为第i种电煤第m周可购订单最大和最小值，取整后为电煤采购模型初始整数决策变量Xi，m .

2.1.2   高斯变异算子

针对GWO算法在电煤采购库存模型求解中早熟收敛的情况，本文受遗传算法的启发，在灰狼种群更新之后增加高斯变异算子以提高局部搜索能力. 高斯变异算子计算公式如下：

X*

i，m = round（Xi，m（1 + g））    （29）

式中：g为满足均值0，方差1的高斯分布随机数;X*

i，m为高斯变异后的第m周第i个煤炭供应商的采购决策变量.

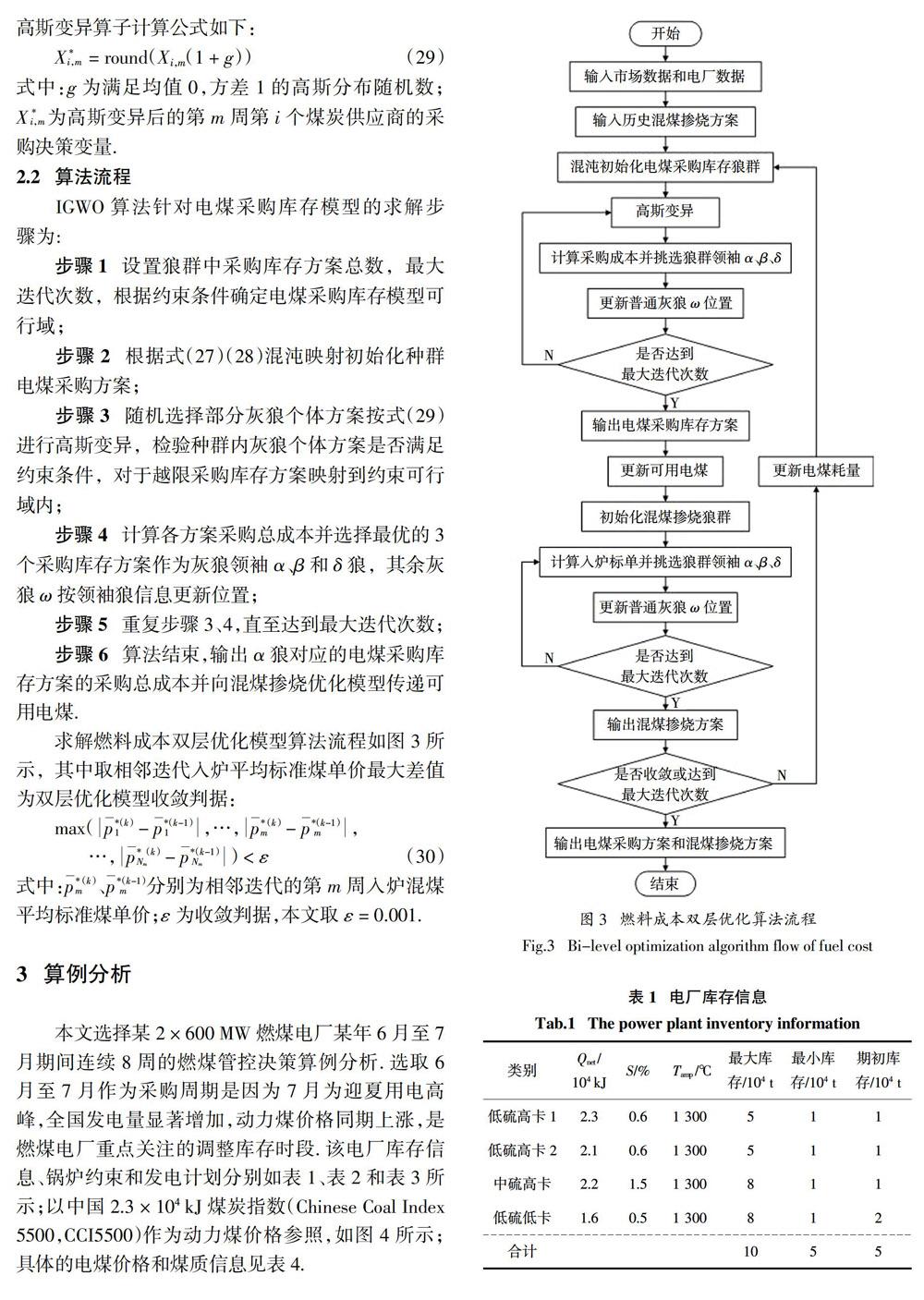
2.2   算法流程

IGWO算法针对电煤采购库存模型的求解步骤为：

步骤1   设置狼群中采购库存方案总数，最大迭代次数，根据约束条件确定电煤采購库存模型可行域;

步骤2   根据式（27）（28）混沌映射初始化种群电煤采购方案;

步骤3   随机选择部分灰狼个体方案按式（29）进行高斯变异，检验种群内灰狼个体方案是否满足约束条件，对于越限采购库存方案映射到约束可行域内;

步骤4   计算各方案采购总成本并选择最优的3个采购库存方案作为灰狼领袖α、β和δ狼，其余灰狼ω按领袖狼信息更新位置;

步骤5   重复步骤3、4，直至达到最大迭代次数;

步骤6   算法结束，输出α狼对应的电煤采购库存方案的采购总成本并向混煤掺烧优化模型传递可用电煤.

求解燃料成本双层优化模型算法流程如图3所示，其中取相邻迭代入炉平均标准煤单价最大差值为双层优化模型收敛判据：

max（[p]*（k）

1       - [p]*（k-1）

1          ，…，[p]*（k）

m       - [p]*（k-1）

m       ，

…，[p]*（k）

Nm       - [p]*（k-1）

Nm       ） < ε       （30）

式中：[p]*（k）

m      、[p]*（k-1）

m       分别为相邻迭代的第m周入炉混煤平均标准煤单价;ε为收敛判据，本文取ε = 0.001.

3   算例分析

本文选择某2 × 600 MW燃煤电厂某年6月至7月期间连续8周的燃煤管控决策算例分析. 选取6月至7月作为采购周期是因为7月为迎夏用电高峰，全国发电量显著增加，动力煤价格同期上涨，是燃煤电厂重点关注的调整库存时段. 该电厂库存信息、锅炉约束和发电计划分别如表1、表2和表3所示;以中国2.3 × 104 kJ煤炭指数（Chinese Coal Index 5500，CCI5500）作为动力煤价格参照，如图4所示;具体的电煤价格和煤质信息见表4.

输入电厂历史混煤掺烧方案，设定最大迭代次数为50，通过求解电煤采购库存模型获得如图5所示的电厂库存曲线. 在采购方案周期内，燃煤电厂在动力煤市场价格上涨时期以购买长协煤为主，稳定发电成本;在现货煤价格较低时，增加现货煤采购量以降低燃料成本. 另外，燃煤电厂通过提前采购下周发电用煤，降低采购成本，实现“价低拉库存，价高保发电”的采购优化目标.

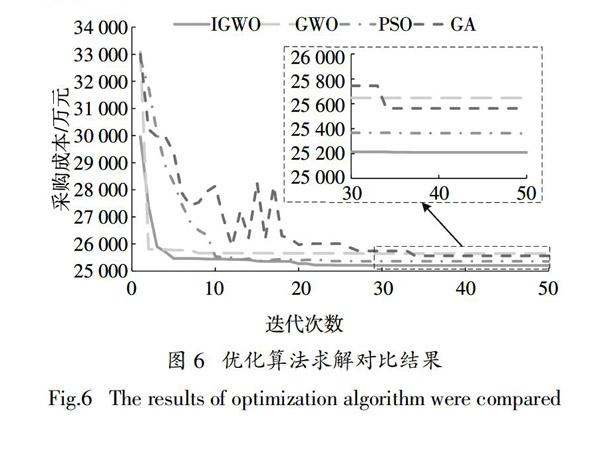
图6为遗传算法（Genetic Algorithm，GA），粒子群优化算法（Particle Swarm Optimization，PSO）以及原始GWO算法与IGWO算法求解性能对比结果. 由图6可知，4种求解算法均能在最大迭代次数内收敛，相较于GA算法和PSO算法，2种GWO算法的采购成本均能迅速下降到最优解附近，然而原始GWO算法陷入局部最优，收敛的解质量最差. 对比4种算法的收敛速度和解的质量，说明IGWO算法在电煤采购库存模型求解拥有更优的全局搜索能力和求解精度.

将上述使用电厂历史混煤配比方案进行电煤采购库存模型求解设置为算例1;将经过一次混煤掺烧优化后再对电煤采购库存模型求解设置为算例2，模拟单独对电厂燃料管控环节优化的情形;使用本文提出的燃料成本双层优化模型模拟电厂整体优化燃料成本方案设置为算例3.

各算例各周入炉标准煤单价求解结果如表5所示. 算例2平均单价较算例1降低35.57元/t，算例3较算例1降低44.27元/t，这是因为算例2受限于电厂可用电煤的数量，混煤配比优化空间有限，而算例3使用燃料成本双层优化模型，电煤采购方案与混煤配比方案协同优化，可以实现锅炉混煤配比方案主动优化效果. 其次，得益于提前购入的低价长协煤，第5周的平均入炉标准煤单价成为各算例中7月单价最低周. 另外，算例3的第4周和第7周入炉标准煤单价在算例1单价相同的情况下分别较第3周和第6周降低2.3元/t、1.2元/t，这是由于燃煤电厂事先签订的供应合同要求必须使用一定数量的高价电煤，当发电量升高时，耗煤量增高，燃煤电厂可以使用更多廉价动力煤，混煤平均入炉标准煤单价随之降低.

算例1、算例2和算例3电煤采购总成本分别为25 358.55万元、23 611.74万元和23 379.78万元，算例2和算例3分别比算例1降低 1 746.81万元、6.89%，1 978.77万元、7.80%，说明对燃煤电厂燃料管控环节优化可以减少电煤采购成本. 本文提出的燃料成本双层优化模型对电煤采购库存管理和混煤配比的协同优化处理可以更为明显地降低电煤采购成本，有效提高燃煤电厂的市场竞争力.

4   结   论

本文构建一种燃煤电厂的燃料成本双层优化模型，并使用改进灰狼优化算法对其求解. 算例结果分析表明：

1）对于电煤采购库存模型中可行解空间复杂且间断的情况，基于混沌初始化与高斯变异的IGWO算法的收敛速度和求解质量优于GA、PSO与GWO，证明了IGWO算法在该模型中具有良好的收敛性和精度.

2）对燃煤电厂燃料管控环节优化可以减少电煤采购成本，而燃料成本双层优化模型兼顾电煤采购方案和混煤配比方案的协同优化，对比传统燃料管控方案与单独管控环节优化方案，在降低采购成本和入炉标准煤单价方面更具优越性.

参考文献

[1]    张艳芹，陈权宝. 国内外煤炭市场价格动态关系研究：基于电煤价格市场化改革前后变化的对比分析[J]. 价格理论与实践，2015（1）：85—87.

ZHANG Y Q，CHEN Q B. Study on the dynamic relationship of coal market price at home and abroad[J]. Price：Theory & Practice，2015（1）：85—87. （In Chinese）

[2]    广东电力交易中心. 广东电力市场 2019 年年度报告[R]. 广州：广东电力交易中心，2020.

Guangdong Power Exchange Center. Annual report of Guangdong power market in 2019[R]. Guangzhou：Guangdong Power Exchange Center，2020. （In Chinese）

[3]    宋永华，包铭磊，丁一，等. 新电改下我国电力现货市场建设关键要点综述及相关建议[J]. 中国电机工程学报，2020，40（10）：3172—3187.

SONG Y H，BAO M L，DING Y，et al. Review of Chinese electricity spot market key issues and its suggestions under the new round of Chinese power system reform[J]. Proceedings of the CSEE，2020，40（10）：3172—3187. （In Chinese）

[4]    黄雷. 火力发电厂燃煤全过程成本分析与优化研究[D]. 北京：华北电力大学（北京），2018：16—24.

HUANG L. Cost analysis and optimization of the whole process coal burning thermal power plant[D]. Beijing：North China Electric Power University，2018：16—24. （In Chinese）

[5]    馬姗姗. 发电企业燃煤库存管理优化研究[D]. 北京：华北电力大学（北京），2014：18—26.

MA S S. Research on the optimization of coal inventory of power plants[D]. Beijing：North China Electric Power University，2014：18—26.（In Chinese）

[6]    张曦木. 火电厂燃煤配比与采购计划优化方法与系统开发[D]. 沈阳：东北大学，2014：17—34.

ZHANG X M. Research on optimization and system design for coal blending and purchase planning in thermal power plants[D]. Shenyang：Northeastern University，2014：17—34. （In Chinese）

[7]    张广宏. 数字燃煤环境下发电企业燃煤库存管理优化研究[D]. 北京：华北电力大学（北京），2016：18—23.

ZHANG G H. Research on optimization of coal inventory management of power plants under digital coal[D]. Beijing：North China Electric Power University，2016：18—23. （In Chinese）

[8]    吳桥. 现货价格波动下原材料最优采购决策研究[D]. 杭州：浙江大学，2012：33—44.

WU Q. Optimal procurement strategies of raw materials under spot price uncertainty[D]. Hangzhou：Zhejiang University，2012：33—44.（In Chinese）

[9]    谢瑛. 煤炭价格波动对火力发电厂经营利润影响风险分析[D]. 北京：华北电力大学（北京），2010：33—55.

XIE Y. The analysis of the efect of coal price fluctuation on the economic benerit of power plant[D]. Beijing：North China Electric Power University ，2010：33—55. （In Chinese）

[10]  石佳星. 考虑动力煤期货的电煤库存优化模型研究[D]. 北京：华北电力大学（北京），2017：19—38.

SHI J X. Research on electricity-coal inventory optimization model considering steam coal futures[D]. Beijing：North China Electric Power University，2017：19—38. （In Chinese）

[11]  杨甲甲，何洋，邹波，等. 电力市场环境下燃煤电厂电煤库存优化的CVaR模型[J]. 电力系统自动化，2014，38（4）：51—59.

YANG J J，HE Y，ZOU B，et al. A CVaR-based coal inventory optimization model for coal-fired power plants in electricity market environment[J]. Automation of Electric Power Systems，2014，38（4）：51—59. （In Chinese）

[12]  黄海东，刘福国，国钦光，等. 配煤掺烧最小煤质偏差模型及煤场存放优化[J]. 热能动力工程，2020，35（5）：97—104.

HUANG H D，LIU F G，GUO Q G，et al. Modeling of minimum coal quality deviation for coal blending and optimization of coal yard storage[J]. Journal of Engineering for Thermal Energy and Power，2020，35（5）：97—104. （In Chinese）

[13]  BAEK S H，PARK H Y，KO S H. The effect of the coal blending method in a coal fired boiler on carbon in ash and NOx emission[J]. Fuel，2014，128：62—70.

[14]  GUERRAS L S，MARTÍN M. Optimal gas treatment and coal blending for reduced emissions in power plants：a case study in Northwest Spain[J]. Energy，2019，169：739—749.

[15]  NAWAZ Z，ALI U. Techno-economic evaluation of different operating scenarios for indigenous and imported coal blends and biomass co-firing on supercritical coal fired power plant performance[J]. Energy，2020，212：118721.

[16]  李金晶，焦开明，赵振宁，等. 火力发电厂配煤掺烧的燃煤成本模型[J]. 中国电力，2018，51（9）：15—19.

LI J J，JIAO K M，ZHAO Z N，et al. Model of coal cost for blending coal combustion in thermal power plant[J]. Electric Power，2018，51（9）：15—19. （In Chinese）

[17]  姚伟，郝兵，刘家利，等. 配煤掺烧方式主要特点及燃煤适应性分析[J]. 中国电力，2018，51（9）：20—27.

YAO W，HAO B，LIU J L，et al. Main characteristics of coal blending method and adaptability analysis for blended coal[J]. Electric Power，2018，51（9）：20—27. （In Chinese）

[18]  刘贵锋，韩雪松. 烟煤锅炉掺烧褐煤对机组安全经济性影响的研究[J]. 中国电力，2018，51（9）：46—52.

LIU G F，HAN X S. Study on the impacts of blending lignite in bituminous coal boiler on unit security and economy[J]. Electric Power，2018，51（9）：46—52.（In Chinese）

[19]  MIRJALILI S，MIRJALILI S M，LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software，2014，69（3）：46—61.

收稿日期：2021-06-23

基金项目：国家自然科学基金资助项目（51937005），National Natural Science Foundation of China（51937005）

作者简介：廖志伟（1973—），男，广西平乐人，华南理工大学副教授

通信联系人，E-mail：epliao@scut.edu.cn