基于集成核熵成分分析算法的工业过程故障检测

郭金玉 赵文君 李元

摘 要：针对核熵成分分析算法（kernel entropy component analysis，KECA）为不同的故障选择相同的核参数影响检测效果的问题，提出了一种基于集成核熵成分分析（ensemble kernel entropy component analysis，EKECA）算法的工业过程故障检测方法。首先，选取一系列具有不同宽度参数的核函数将非线性数据投影到核特征空间，选取Rényi熵值贡献较大的特征值和特征向量，得到转换后的得分矩阵，建立多个KECA子模型;然后，将测试数据投影到各KECA子模型上，计算各KECA子模型的统计量，得到检测结果;最后，将各KECA子模型的检测结果利用Bayesian决策进行概率换算，利用集成学习法计算检测结果统一的统计量，判断其是否超出控制限，并将该算法应用于数值例子和TE过程。仿真结果表明，与传统的EKPCA，KECA等算法相比，所提方法有效提高了故障检测率，降低了误报率。新方法解决了传统KECA算法中不同故障核参数的选择问题，为提高KECA算法在非线性工业过程故障检测中的性能提供了参考。

关键词：自动控制技术其他学科;核熵成分分析;高斯核函数;Bayesian决策;集成学习法

中图分类号：TP277   文献标识码：A

doi：10.7535/hbkd.2021yx05006

收稿日期：2021-06-03;修回日期：2021-09-30;责任编辑：王淑霞

基金项目：国家自然科學基金（61673279）;辽宁省教育厅一般项目（LJ2019007）

第一作者简介：郭金玉（1975—），女，山东高唐人，副教授，博士，主要从事故障诊断、生物特征识别算法及应用方面的研究。

E-mail：969554959@qq.com

Fault detection of industrial process based on ensemble kernel entropy component analysis algorithm

GUO Jinyu，ZHAO Wenjun，LI Yuan

（College of Information Engineering，Shenyang University of Chemical Technology，Shenyang Liaoning，110142，China）

Abstract：To solve the problem caused by kernel entropy component analysis （KECA） for selecting the same kernel parameters for different faults，a fault detection of industrial process based on ensemble kernel entropy component analysis （EKECA） was proposed.Firstly，a series of kernel functions with different width parameters were selected to project the nonlinear data into the kernel feature space.The eigenvalues and eigenvectors with large contribution to Rényi entropy were selected to obtain the transformed score matrix.The multiple KECAsubmodels were established.Secondly，the test data were projected onto each KECA submodel.The statistics of each KECA submodel were calculated to obtain the detection results.Finally，the detection results of each KECA submodel were turned into probability by Bayesian decision.The unified statistics were calculated by ensemble learning strategy and judged whether it exceeds the control limit.The algorithm was applied to a numerical example and the TE process.The simulation results show that the proposed algorithm can effectively improve the fault detection rate and reduce the false alarm rate compared with traditional EKPCA，KECA and other algorithms.This method solves the problem of selecting kernel parameters for different faults in the traditional KECA algorithm and provides a reference for improving the performance of KECA algorithm in fault detection of nonlinear industrial processes.

Keywords：

other disciplines of automatic control technology;kernel entropy component analysis;Gaussian kernel function;Bayesian decision;ensemble learning method

在流程工业和制造业中，随着现代制造业的快速发展，对高质量产品的需求不断增加，保证系统正常运行成为一项至关重要的任务。虽然运行过程中的标准控制器可以补偿许多类型的干扰，但也存在控制器无法完全处理的变化，将这种特征属性或变量不允许的偏差定义为故障。随着新仪器和通信技术的发明，人们可以从工厂装置中收集大量的实时过程数据，通过监测收集到的数据来识别过程中的异常情况。因此，多元统计过程监控（multivariate statistical process monitoring，MSPM）方法[1-4]在过去几十年中得到了发展。

在MSPM方法中，主成分分析[5-8]（principal component analysis，PCA）是应用最广泛的一种。它通过构造原始数据最大方差的低维空间来压缩数据，将监测数据投影到该空间以捕获偏差进行过程监测。与PCA相比，核主元分析（kernel principal component analysis，KPCA）可以处理非线性系统[9-13]。传统KPCA方法的不足阻碍了对过程数据变化的观察，且由KPCA模型生成的特征值矩阵没有得到足够的重视，如何从动态过程中有效获取重要信息还需要进一步研究。KANO等[14]根据特征值评估差异性提出一种称为DISSIM的统计监测方法，但他们建立的监测计算公式难以确定最优时间窗口的大小。JOHANNESMEYER等[15]基于相似性提出将snapshopt数据与分割的历史数据进行比较，进而对数据进行监测，但是比较对象是T2和SPE统计量，其计算量比特征矩阵大。JOSHPH等[16]提出块增量核主元分析（chunk incremental kernel principal component analysis，CIKPCA）算法。普通算法在信息特征提取方面用時较长，CIKPCA算法弥补了此缺陷，加快了提取速度。然而，CIKPCA算法只能获取和保留原始样本的全局特征，不能很好地保留局部特征。

JENSSEN[17]提出核熵成分分析（kernel entropy component analysis，KECA）算法，该算法用于处理非线性原始数据的降维和矩阵转换，已应用于工业过程检测[18]。与KPCA类似，核熵成分分析可以处理非线性系统，但与KPCA不同的是，KECA算法通过选取对熵值贡献最大的前k个特征向量作为投影方向，在保证熵值损失最小的情况下进行故障检测。JIANG等[19] 验证了KECA算法在工业过程监测方面具有优越的可行性和有效性。韩宇等[20]提出在监督学习和无监督学习下建立KECA模型，进而使用Bayesian方法对工业过程故障进行检测。齐咏生等[21]提出采用改进KECA算法监测统计量的方法。该算法根据KECA的特性构造新的检测方式，其微小故障检测效果虽然高于传统的监测统计量，但检测效果仍然不理想。传统的KECA算法通常采用经验法确定核函数中的宽度参数c，对不同的故障使用相同的参数，影响其检测效果。针对KECA算法中核参数的选择问题，本文利用Bayesian决策[22]和集成学习法[23]提出了集成核熵成分分析（ensemble kernel entropy component analysis，EKECA）算法。通过建立一系列的子KECA模型，使不同的故障选择不同的宽度参数，然后计算各子模型的检测结果，并使用Bayesian决策将其转化为概率的形式。为了组合各子模型的故障概率，选用集成学习算法，弥补因核参数选择不合理导致检测效果差的不足。

1 集成核熵成分分析算法

2 基于集成核熵成分分析算法的建模与检测

基于集成核熵成分分析算法的工业过程故障检测分为离线建模和在线检测。基于集成核熵成分分析算法的故障检测流程图如图1所示。

2.1 离线建模

1）获取训练数据：获取包含m个变量和n个样本的训练数据集X=[x1，x2，…，xn]∈Rm×n，对X进行标准化处理;

2）选择一系列具有不同宽度参数的高斯核函数k（j）（x，xt）=exp[-（‖x-xt‖2/（2j-1rnσ2））]，j=1，2，…，ns为核函数的个数;

3）对于每个高斯核函数，根据式（5）获得熵贡献较大的特征值和特征向量，定义核主元分析主轴张成的子空间为U（j）k，建立一系列KECA子模型;

4）将训练数据集通过非线性函数Φ映射到U（j）k上，根据式（12）得到各子模型的得分矩阵T（j）k;

5）根据式（14）和式（15）分别计算各子模型的监测统计量SPE（j）和T2（j）;

6）令检验水平为β，利用核密度估计方法确定各子模型统计量的控制限SPE（j）lim和T2（j）lim。

2.2 在线检测

1）对测试数据Xnew根据训练数据的均值和方差进行标准化处理;

2）将测试数据投影到各个子模型上，通过式（13）得到得分矩阵Tknew（j）;

3）根据式（14）和（式15），分别计算各个子模型中测试数据的监测统计量SPE（j）和T2（j）;

4）通过式（16）-式（23），将每个子模型的监测统计量转换成故障发生的概率;

5）通过式（24）和式（25），组合各子模型的检测结果，计算统一的监测统计量ESPE和ET2;

6）将统一的统计量ESPE和ET2与检验水平β对比，若统计量大于检验水平则视为故障。

3 仿真结果与分析

3.1 数值仿真结果与分析

本文构造一个数值例子，该数据有3个变量，模型如下：

x1x2x3=rr2-3r-r3+3r2+e1e2e3，（26）

式中：[e1，e2，e3]T服从高斯分布，均值为0，标准差为0.01;r服从均匀分布。为了便于说明，由式（26）生成500个样本作为正常数据，利用这些数据构造常规的核熵成分分析模型，并设定99%的置信限进行状态判断。根据数值例子创建2种不同的故障数据，在生成故障数据集的过程中设定微小故障。

故障1：变量x3从第161个样本到第500个样本发生0.001 5×（i-160）的微小斜坡变化。

故障2：变量x2从第201个样本到第500个样本发生幅值大小为0.012的微小阶跃变化。

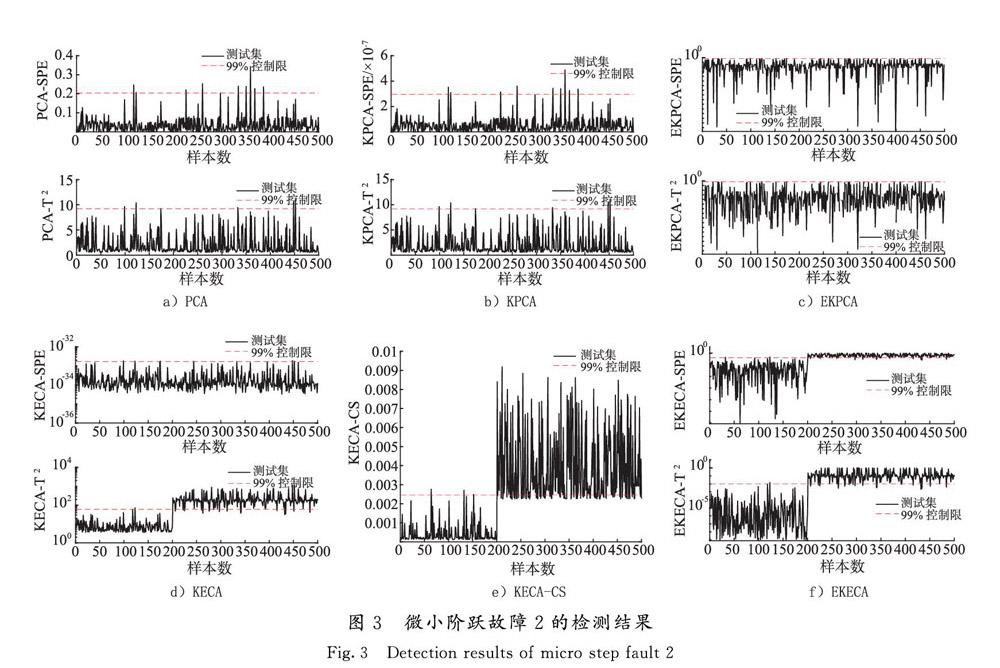
每个故障类型产生500个样本作为测试数据。图2和图3分别为PCA，KPCA，EKPCA，KECA，KECA-CS和EKECA对微小斜坡故障和阶跃故障的检测结果。由图2 a）和图3 a）可知，PCA算法的SPE和T2统计量几乎检测不出故障。主要原因是PCA是线性算法，对非线性数据的检测效果较差;由图2 b）和图3 b）可知，与PCA类似，KPCA算法的2个统计量几乎检测不出故障，主要原因是KPCA通过奇异值分解（singular value decomposition，SVD）生成特征矩阵，实现对非线性数据降维，但在数据变换的过程中可能会导致特征矩阵中的信息丢失，而且对不同的故障运用相同的核参数，从而导致检测效果较低;由图2 c）和图3 c）可知，EKPCA完全检测不出故障，主要原因是EKPCA算法仅解决了核参数选择的问题，并未解决传统KPCA在数据变换时导致特征矩阵信息丢失的问题，故检测效果较差;由图2 d）和图3 d）可知，KECA中仅T2统计量检测出故障，SPE统计量几乎检测不出故障。主要原因是KECA算法根据Rényi熵值来选取核特征矩阵的特征值，解决了传统KPCA算法特征矩阵丢失重要信息的问题，但KECA对不同的故障运用相同的核参数，建立的单个模型不适用于所有故障，故检测效果不佳;由图2 e）和图3 e）可知，虽然KECA-CS算法对微小故障检测效果高于传统的KECA，但检测效果仍不理想，主要原因是KECA-CS没有解决核参数的选择问题;由图2 f）和图3 f）可知，EKECA算法能够在主元空间和残差空间中以较低的误报率及时监测出故障的发生。综上所述，与其他5种方法相比，EKECA算法在故障发生前基本没有超过控制限，误报率较低，且在故障发生时及时触发报警，检测效果较好。主要原因是EKECA算法根据非线性数据变换的方法，有效地计算出输入空间数据集的最大Rényi熵值，既解决了数据变化前后的熵损失问题，又解决了传统KECA算法中不能很好地选择核参数的问题，将具有不同核参数子模型的监测统计量利用Bayesian决策转化成概率的形式，通过集成算法进行组合形成统一的统计量，适用于检测不同类型的故障。

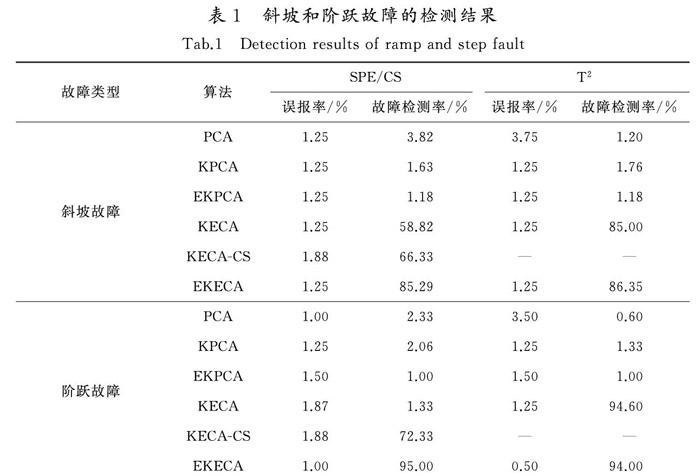
表1为斜坡和阶跃故障的检测结果。由表1可以看出，PCA，KPCA，EKPCA，KECA和KECA-CS 5种算法的故障检测率较低，而EKECA在保证误报率较低的情况下，具有较高的故障检測率，验证了该方法在非线性数据故障检测中的有效性。

3.2 TE仿真结果与分析

为了更有效地说明EKECA算法的有效性，将该算法应用到TE仿真平台进行验证。TE工业生产过程广泛应用于故障检测研究领域[24]。TE工业流程主要有5个操作单元：反应器、产品冷凝器、循环压缩机、气液分离器和产品汽提器[18，25-26]。考虑到过程中变量可能受到任何变化的影响，将TE流程的21个预定义的异常操作事件编入系统，并收集相应过程的数据。每组采集的数据集由960个样本组成，人为故障从第161个样本引入。在21个故障中，由于一些故障比较容易识别，故排除这些容易识别的故障。因此，选用故障4，10，15，19和20来测试所提方法的有效性，如表2所示。

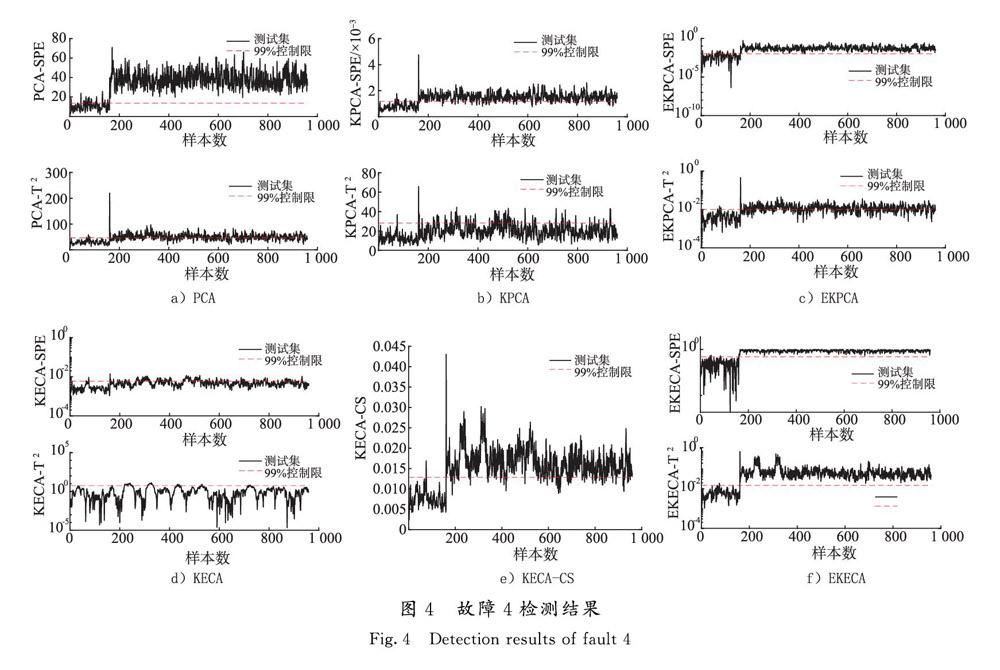
6种算法对故障4的检测结果如图4所示。从检测结果图可以看出PCA算法与EKPCA类似，SPE统计量能保证在误报率较低的情况下检测出故障，但T2统计量一直在控制限周围波动，检测效果较差;KPCA算法的SPE统计量虽然能检测出故障，但检测率较低，T2统计量的检测效果较差;EKPCA算法的SPE统计量检测出故障但误报指标较高，而T2统计量一直在控制限周围波动，故障检测率较低;KECA算法的2个统计量基本检测不出故障的发生;KECA-CS算法的检测效果好于KECA，但是仍有漏报;而本文所提出的EKECA算法不仅误报率较低，当故障发生时也能及时报警。主要原因是EKECA算法根据非线性数据的变换方法，保持了输入空间的最大Rényi值，又解决了不同故障核参数的选择问题。

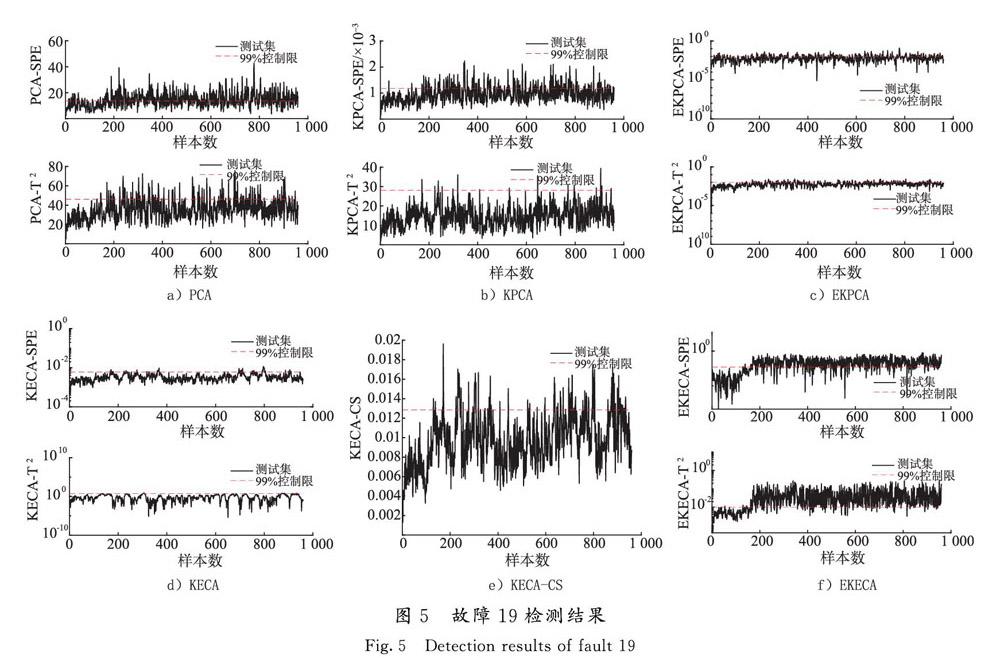
6种方法对故障19的检测结果如图5所示，可以看到PCA和KPCA算法的SPE统计量虽然检测出部分故障，但故障检测率较低，且有较多的正常样本在控制限上方，误报率较高，而T2统计量的漏报现象比较严重;EKPCA，KECA和KECA-CS算法的漏报现象也比较严重，且KECA算法的统计量基本都在控制限以下，检测效果较差;相对其他5种算法，EKECA算法的SPE统计量在保证误报率较低的情况下，检测出大部分故障，T2统计量在故障发生时不仅及时检测出故障的发生，且误报样本较少，在保证较低误报率的情况下故障检测率较高。

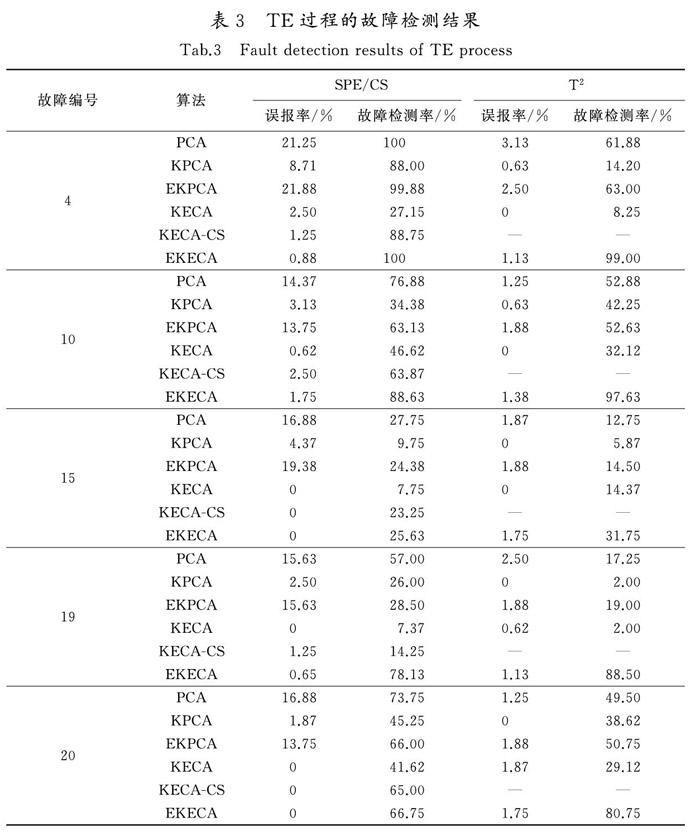
为了更简明地证明本文所提方法的有效性，表3列出了EKECA算法与PCA，KPCA，EKPCA，KECA和KECA-CS算法的对比情况。以故障4为例，由表3可以看出，PCA算法的SPE统计量虽检测率为100%，但误报率较高，而T2统计量的故障检测率较低，故PCA的检测效果不佳;KPCA的SPE统计量不能保证在误报率较低的情况下达到较高的故障检测率，且T2统计量的检测率较低;与PCA类似，EKPCA在残差空间虽有较高的检测率，但误报率较高，且主元空间的检测效果不佳，故障检测率较低;KECA的2个统计量的故障检测率较低，检测效果较差;KECA-CS虽然在保证误报率较低的情况下提高了故障检测率，但检测效果仍不理想;而EKECA算法的SPE和T2统计量在保证误报率指标较低的情况下故障检测率较高，验证了EKECA算法在非线性数据故障检测中的有效性。

4 结 语

本文提出了一种基于集成核熵成分分析算法的工业过程故障检测方法。利用一系列具有不同宽度参数的高斯核函数将原始数据映射到核特征空间，然后对核矩阵进行特征值分解获取特征值和特征向量，计算特征向量所对应的熵值的贡献，选取前k个最大贡献的特征向量作为投影方向，从而解决了数据变化前后的熵损失问题。将不同模型的检测结果通过Bayesian决策转换成故障发生的概率形式，然后通过集成学习法将各故障的概率进行组合，实现故障检测。

EKECA算法有效解决了传统KECA算法对不同故障核参数选择不合理的问题。将该算法应用于数值例子和TE过程的仿真实验，并与其他故障检测方法进行比较，表明了该方法的有效性。

本文方法虽然能检测出TE过程中的大部分故障，但对于一些未知故障（故障19和20）仅提高了故障检测率，却未能完全检测出故障。因此，未来将继续改进算法，提高对未知故障的检测率。

参考文献/References：

[1] 文成林，吕菲亚，包哲静，等.基于数据驱动的微小故障诊断方法综述[J].自动化学报，2016，42（9）：1285-1299.

WEN Chenglin，LYU Feiya，BAO Zhejing，et al.A review of data driven-based incipient fault diagnosis[J].Acta Automatica Sinica，2016，42（9）：1285-1299.

[2] HUANG J P，YAN X F.Quality-driven principal component analysis combined with kernel least squares for multivariate statistical process monitoring[J].IEEE Transactions on Control Systems Technology，2019，27（6）：2688-2695.

[3] ROSSOUW R F，COETZER R L J，LE ROUX N J.Variable contribution identification and visualization in multivariate statistical process monitoring[J].Chemometrics and Intelligent Laboratory Systems，2020，196：103894.

[4] YANG W A.Monitoring and diagnosing of mean shifts in multivariate manufacturing processes using two-level selective ensemble of learning vector quantization neural networks[J].Journal of Intelligent Manufacturing，2015，26（4）：769-783.

[5] 赵帅，宋冰，侍洪波.基于加权互信息主元分析算法的质量相关故障检测[J].化工学报，2018，69（3）：962-973.

ZHAO Shuai，SONG Bing，SHI Hongbo.Quality-related fault detection based on weighted mutual information principal component analysis[J].CIESC Jorunal，2018，69（3）：962-973.

[6] DU Y C，DU D P.Fault detection and diagnosis using empirical mode decomposition based principal component analysis[J].Computers & Chemical Engineering，2018，115：1-21.

[7] GUEDDI I，NASRI O，BENOTHMAN K，et al.Fault detection and isolation of spacecraft thrusters using an extended principal component analysis to interval data[J].International Journal of Control Automation and Systems，2017，15（2）：776-789.

[8] HAMADACHE M，LEE D.Principal component analysis based signal-to-noise ratio improvement for inchoate faulty signals：Application to ball bearing fault detection[J].International Journal of Control Automation and Systems，2017，15（2）：506-517.

[9] 翟坤，杜文霞，呂锋，等.一种改进的动态核主元分析故障检测方法[J].化工学报，2019，70（2）：716-722.

ZHAI Kun，DU Wenxia，LYU Feng，et al.Fault detect method based on improved dynamic kernel principal component analysis[J].CIESC Jorunal，2019，70（2）：716-722.

[10]邓佳伟，邓晓刚，曹玉苹，等.基于加权统计局部核主元分析的非线性化工过程微小故障诊断方法[J].化工学报，2019，70（7）：2594-2605.

DENG Jiawei，DENG Xiaogang，CAO Yuping，et al.Incipient fault diagnosis method of nonlinear chemical process based on weighted statistical local KPCA[J].CIESC Jorunal，2019，70（7）：2594-2605.

[11]SHIOKAWA Y，DATE Y，KIKUCHI J.Application of kernel principal component analysis and computational machine learning to exploration of metabolites strongly associated with diet[J].Scientific Reports，2018，8（1）：3426.

[12]SOH W，KIM H，YUM B J.Application of kernel principal component analysis to multi-characteristic parameter design problems[J].Annals of Operations Research，2018，263（1）：69-91.

[13]HUANG J，YAN X F.Related and independent variable fault detection based on KPCA and SVDD[J].Journal of Process Control，2016，39：88-99.

[14]KANO M，HASEBE S，HASHIMOTO I，et al.Statistical process monitoring based on dissimilarity of process data[J].AIChE Journal，2002，48（6）：1231-1240.

[15]JOHANNESMEYER M C，SINGHAL A，SEBORG D E.Pattern matching in historical data[J].AIChE Journal，2002，48（9）：2022-2038.

[16]JOSHPH A A，TOKUMOTO T，OZAWA S.Online feature extraction based on accelerated kernel principal component analysis for data stream[J].Evolving Systems，2016，7（1）：15-27.

[17]JENSSEN R.Kernel entropy component analysis[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2010，32（5）：847-860.

[18]YANG Y H，LI X L，LIU X Z，et al.Wavelet kernel entropy component analysis with application to industrial process monitoring[J].Neurocomputing，2015，147：395-402.

[19]JIANG Q C，YAN X F，LYU Z M，et al.Fault detection in nonlinear chemical processes based on kernel entropy component analysis and angular structure[J].Korean Journal of Chemical Engineering，2013，30（6）：1181-1186.

[20]韓宇，李俊芳，高强，等.基于故障判别增强KECA算法的故障检测[J].化工学报，2020，71（3）：1254-1263.

HAN Yu，LI Junfang，GAO Qiang，et al.Fault detection based on fault discrimination enhanced kernel entropy component analysis algorithm[J].CIESC Jorunal，2020，71（3）：1254-1263.

[21]齐咏生，张海利，高学金，等.基于KECA的化工过程故障监测新方法[J].化工学报，2016，67（3）：1063-1069.

QI Yongsheng，ZHANG Haili，GAO Xuejin，et al.Novel fault monitoring strategy for chemical process based on KECA[J].CIESC Journal，2016，67（3）：1063-1069.

[22]YU C M，PAN Q，CHENG Y M，et al.A kernel-based bayesian classifier for fault detection and classification[C]// 2008 7th World Congress on Intelligent Control and Automation，Chongqing：IEEE，2008：124-128.

[23]JIANG H，QIU X J，CHEN J，et al.Insulator fault detection in aerial images based on ensemble learning with multi-level perception[J].IEEE Access，2019，7：61797-61810.

[24]吕永艳，马洁.基于KPCA的多工况TE过程故障检测研究[J].北京信息科技大学学报（自然科学版），2016，31（6）：32-36.

LYU Yongyan，MA Jie.Fault detection of multi-condition TE process based on KPCA[J].Journal of Beijing Information Science & Technology University，2016，31（6）：32-36.

[25]LEE C J，LEE G，LEE J M.A fault magnitude-based strategy for effective fault diagnosis and isolation[J].Journal of Chemical Engineering of Japan，2015，48（1）：44-51.

[26]YIN S，DING S X，HAGHANI A，et al.A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process[J].Journal of Process Control，2012，22（9）：1567-1581.