基于CEEMD-GRU组合模型的快速路短时交通流预测
沈富鑫 邴其春 张伟健 胡嫣然 高鹏


摘 要:為了提高短时交通流预测精度,提出了基于互补集成经验模态分解(complementary ensemble empirical mode decomposition,CEEMD)和门控循环单元(Gated Recurrent Unit,GRU)组合模型的快速路短时交通流预测方法。首先,运用互补集成经验模态分解算法,将非稳定的原始交通流时间序列数据分解为相对平稳的多个模态分量;然后,将分解后的模态分量分别建立GRU模型进行单步预测;最后,叠加每个分量的预测值,获取最终预测结果,并采用上海市南北高架快速路实测交通流数据进行实例验证。结果表明:CEEMD-GRU组合模型的预测效果明显优于GRU神经网络模型、EMD-GRU组合模型以及EEMD-GRU组合模型,平均预测精度分别提升了33.4%,25.6%和18.3%。CEEMD-GRU组合模型能够有效提取交通流数据特征分量,提高预测精度,为交通管控提供科学决策依据。
关键词:公路运输管理;城市快速路;短时交通流预测;互补集成经验模态分解;门控循环单元神经网络
中图分类号:U491 文献标识码:A
doi:10.7535/hbkd.2021yx05003
收稿日期:2021-06-15;修回日期:2021-08-15;责任编辑:张士莹
基金项目:山东省重点研发计划项目(2019GGX101038);国家自然科学基金(51678320);山东省自然科学基金(ZR2019MG012)
第一作者简介:沈富鑫(1992—),男,山东安丘人,硕士研究生,主要从事智能交通系统关键理论与技术方面的研究。
通讯作者:邴其春副教授。E-mail:bingqichun@163.com
Short-term traffic flow prediction of expressway based on CEEMD-GRU combination model
SHEN Fuxin1,BING Qichun1,ZHANG Weijian1,HU Yanran1,GAO Peng2
(1.School of Mechanical and Automotive Engineering,Qingdao University of Technology,Qingdao,Shandong 266520,China;2.Qingdao Transportation Public Service Center,Qingdao,Shandong 266100,China)
Abstract:In order to improve the accuracy of short-term traffic flow prediction,a short-term traffic flow prediction method of expressway based on the combined model of complementary ensemble empirical mode decomposition (CEEMD) and gated recurrent unit (GRU) was proposed.Firstly,the unstable original traffic flow time series data were decomposed into relatively stable multiple modal components by complementary ensemble empirical mode decomposition algorithm.Then,a GRU model was established for each decomposed modal component sequence for one-step prediction.Finally,the predicted value of each component was superimposed to obtain the final prediction result,and the measured traffic flow data of north-south elevated expressway in Shanghai was used to verify and analyze the model.The experimental results show that the prediction effect of CEEMD-GRU combination model is superior to GRU neural network model,EMD-GRU combination model and EEMD-GRU combination model,and the average prediction accuracy is improved by 33.4%,25.6% and 18.3%,respectively.CEEMD-GRU combination model can effectively extract the characteristic components of traffic flow data and improve the prediction accuracy,which provides scientific decision-making basis for traffic control management.
Keywords:
road transportation management;urban expressway;short-term traffic flow prediction;complementary ensemble empirical mode decomposition;gated recurrent unit neural network
精准的短时交通流预测信息是智能交通系统中的关键部分。随着汽车保有量的增加以及人们对通行的要求不断提高,交通污染、交通拥挤、交通事故等一系列交通问题严重影响着城市居民的日常生活品质。准确的短时交通流预测结果不仅可以帮助人们选择合适的交通工具、缩短出行时间,也是实现主动交通管制的关键。近几十年来,国内外专家、学者都在深入探究精度更高的交通流预测方法。现有交通流预测方法主要包括时间序列模型、卡尔曼滤波模型、支持向量回归模型和组合模型[1-4]。
随着大数据技术的发展,以数据驱动为基础的交通流预测模型受到广泛关注。以数据为驱动的交通流预测主要包括数据处理和机器学习2种方式。数据处理通常用于数据去噪、数据分解和数据重构等方面,用来提取原始交通流数据的显著特征。其中,小波分解(WD)和经验模态分解(EMD)以及集成经验模态分解(EEMD)是几种主要的数据分解算法,大量研究和实例也证明了这些分解算法的有效性。例如,XIE等[5]将2种小波模型与卡尔曼滤波相结合进行短时交通流预测,实验结果证明小波卡尔曼滤波通过消除噪声影响,可以表现出更好的性能。谭满春等[6]运用小波变换降低原始交通流数据中心的噪声,构建了基于去噪数据集和混合交通流预测模型。WEI等[7]将经验模态分解(EMD)与BP神经网络(BPNN)原理相结合,用于地铁系统短期客流預测领域,证实了方法的有效性。YANG等[8]提出了一种基于经验模式分解模型和堆叠式自动编码器模型的混合交通流多步预测方法,提高了交通流多步预测精度。陆文琦等[9]将原始速度序列用集成经验模态分解算法进行分解重构,构建了一种基于混合深度学习(hybrid deep learning,HDL)的车辆速度预测模型。LI等[10]提出了一种基于集成经验模态分解和随机向量函数连接网络的行程时间预测模型。随着计算机技术的发展,机器深度学习算法在数据挖掘方面的优异性能为交通流预测领域带来了全新思路。MA等[11]等将长短时记忆(LSTM)模型运用到交通流预测领域,克服了记忆模块后向传播误差衰减问题;TIAN等[12]通过实例验证和几种模型的对比,证实了循环神经网络在预测方面的优势;RUI等[13]将LSTM和GRU组合模型运用到交通流预测领域,验证了其预测性能比ARIMA方法更优;罗向龙等[14]采用K-近邻(KNN)算法构建交通流序列中的数据集,并用LSTM模型进行训练、预测,模型表现出更高的精度;于德新等[15]将构建的GRU-RNN模型与BP神经网络作比对,证实了GRU-RNN模型拟合度高、误差小。
综上算法和预测模型可知,虽然人们在交通流预测方面取得了一定的成果,但是仍然存在一些不足。如WD和WPD算法主要依赖于基函数选择,适应性相对较差;EMD算法在进行分解时会出现端点效应及模态混叠等问题;经改进后的EEMD算法尽管在一定程度上克服了模态混叠现象,但增加了噪声影响,稳定性也较差。为了更好地提取交通流数据特征分量,充分发挥深度学习网络模型在交通流预测方面的优势,提高交通流预测的精度,笔者提出了基于互补集成经验模态分解(complementary ensemble empirical mode decomposition,CEEMD)和门控循环单元(gated recurrent unit,GRU)组合模型的快速路短时交通流预测方法。
1 CEEMD和GRU组合模型的构建
1.1 互补集成经验模态分解
互补集成经验模态分解是以EMD[16](empirical mode decomposition)理论为基础,在EEMD[17]上进行改进的一种新型自适应分解算法,由YEH等[18]于2010年提出。在CEEMD算法中,通过成对地添加白噪声到原始数据中,生成2组总体内模函数。因此,可以通过内模函数推导出由原始数据和附加噪声组成的2种混合,不但可以有效克服EMD中的模态混叠现象,还可以很大程度地消除在CEEMD中添加的白辅助噪声残留,提高分解的计算效率。具体步骤如下。
1)在原始信号中添加n对正负相反的白噪声,可得M1M2=111-1SN。式中:S表示原始数据;N表示加入的白噪声;M1表示带正噪声的原始数据之和;M2表示带负噪声的原始数据之和。
2)对得到的集合信号用EMD算法进行分解,可以在每个信号中对应得到一组IMF,将第i个信号的第j个IMF记为cij。
3)将得到的2n组IMF取平均值,分解结果cj=12n∑2ni=1cij,式中cj表示分解完成后得到的第j个IMF分量。
1.2 门控循环单元深度网络
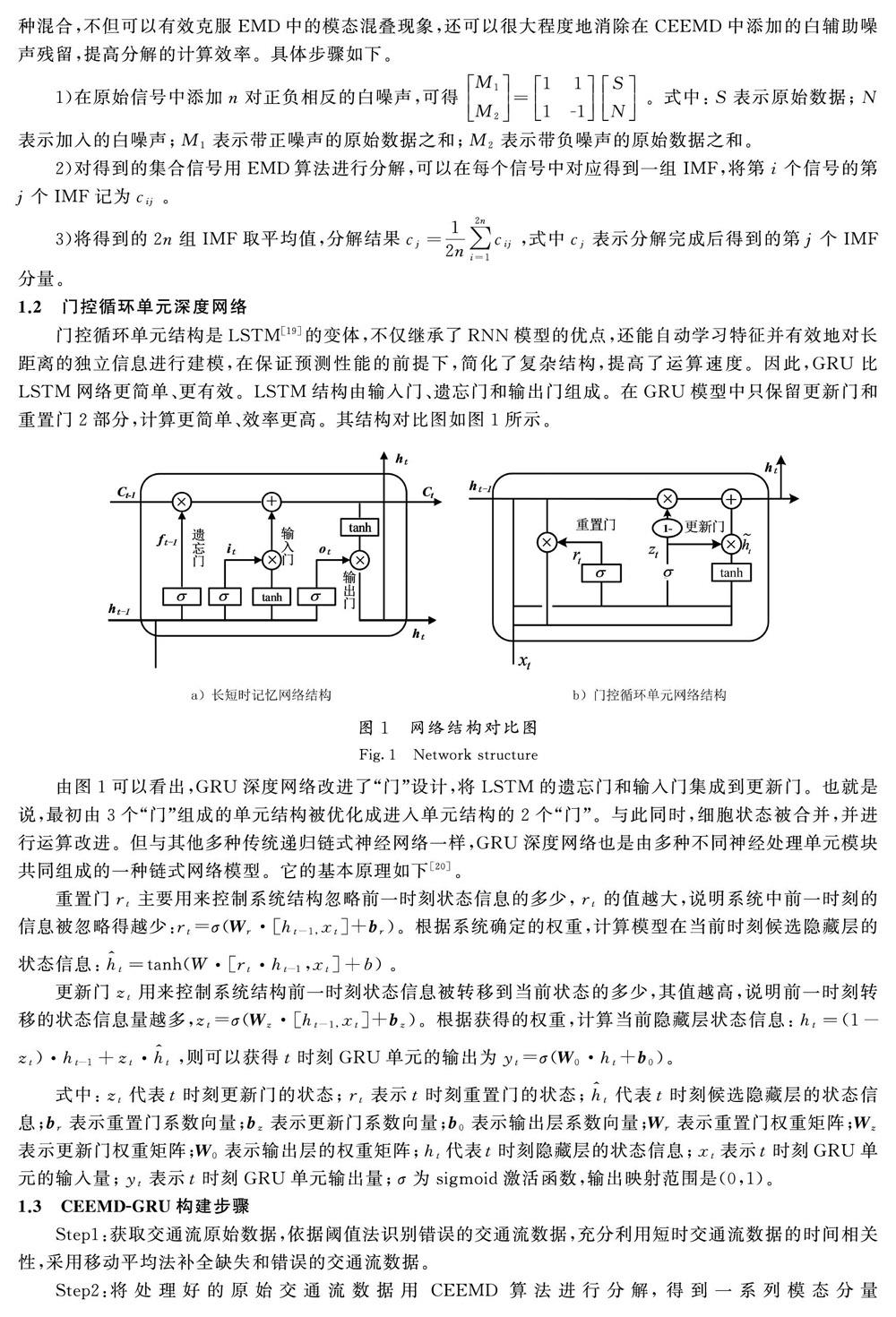
门控循环单元结构是LSTM[19]的变体,不仅继承了RNN模型的优点,还能自动学习特征并有效地对长距离的独立信息进行建模,在保证预测性能的前提下,简化了复杂结构,提高了运算速度。因此,GRU比LSTM网络更简单、更有效。LSTM结构由输入门、遗忘门和输出门组成。在GRU模型中只保留更新门和重置门2部分,计算更简单、效率更高。其结构对比图如图1所示。
由图1可以看出,GRU深度网络改进了“门”设计,将LSTM的遗忘门和输入门集成到更新门。也就是说,最初由3个“门”组成的单元结构被优化成进入单元结构的2个“门”。与此同时,细胞状态被合并,并进行运算改进。但与其他多种传统递归链式神经网络一样,GRU深度网络也是由多种不同神经处理单元模块共同组成的一种链式网络模型。它的基本原理如下[20]。
重置门rt主要用来控制系统结构忽略前一时刻状态信息的多少,rt的值越大,说明系统中前一时刻的信息被忽略得越少:rt=σ(Wr·[ht-1,xt]+br)。根据系统确定的权重,计算模型在当前时刻候选隐藏层的状态信息:h^t=tanh(W·[rt·ht-1,xt]+b)。
更新门zt用来控制系统结构前一时刻状态信息被转移到当前状态的多少,其值越高,说明前一时刻转移的状态信息量越多,zt=σ(Wz·[ht-1,xt]+bz)。根据获得的权重,计算当前隐藏层状态信息:ht=(1-zt)·ht-1+zt·h^t,则可以获得t时刻GRU单元的输出为yt=σ(W0·ht+b0)。
式中:zt代表t时刻更新门的状态;rt表示t时刻重置门的状态;h^t代表t时刻候选隐藏层的状态信息;br表示重置门系数向量;bz表示更新门系数向量;b0表示输出层系数向量;Wr表示重置门权重矩阵;Wz表示更新门权重矩阵;W0表示输出层的权重矩阵;ht代表t时刻隐藏层的状态信息;xt表示t时刻GRU单元的输入量;yt表示t时刻GRU单元输出量;σ为sigmoid激活函数,输出映射范围是(0,1)。
1.3 CEEMD-GRU构建步骤
Step1:获取交通流原始数据,依据阈值法识别错误的交通流数据,充分利用短时交通流数据的时间相关性,采用移动平均法补全缺失和错误的交通流数据。
Step2:将处理好的原始交通流数据用CEEMD算法进行分解,得到一系列模态分量IMF1,IMF2,IMF3,…,IMFn和1个残余分量rn。
Step3:将分解后得到的相对平稳的交通流模态分量数据输入到GRU深度网络中,建立CEEMD-GRU预测模型。
Step4:输入模型各模态分量数据,用前4日数据对模型进行训练,输出第5日各模态分量的预测值。
Step5:将输出的各模态分量预测值进行叠加,获取最终交通流时间序列预测值。
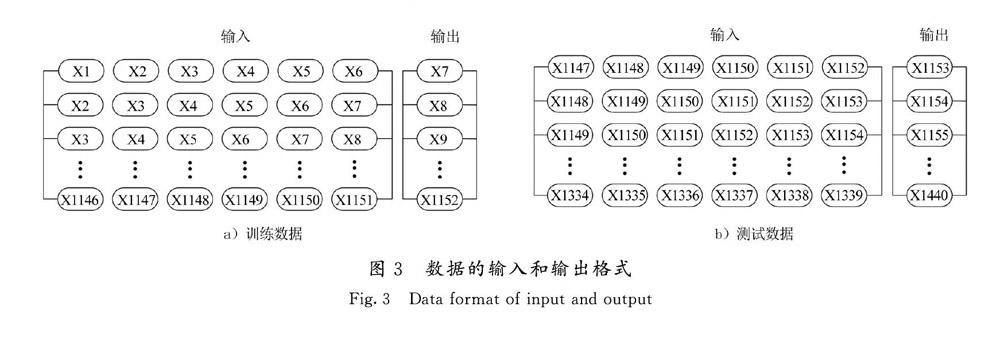
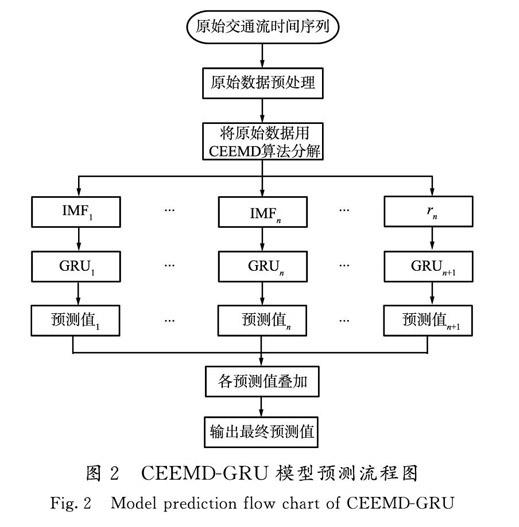
CEEMD-GRU模型预测流程图如图2所示,将Step4中模型输入维数设置为6,数据训练和预测的输入、输出格式如图3所示。
2 结果验证及分析
2.1 数据来源
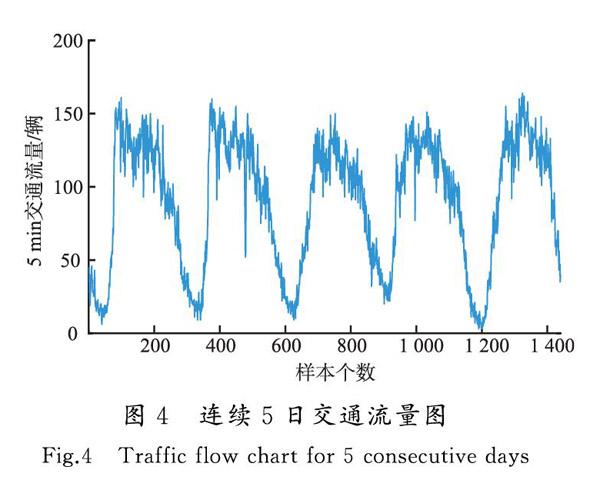
为了确保预测结果真实有效,本文收集的数据来自上海市南北高架路感应线圈实测交通流量数据,采集时间为2018-08-27至2018-08-31连续5日的交通流数据,采集周期为5 min,共获取1 440个实际交通流数据。其交通流量变化趋势见图4。
由连续5日的交通流数据可以看出,由于人们生活、工作出行的规律性,使得交通流变化趋势呈现出明显的周期性,每5 min交通流量在0~180辆之间波动。
2.2 CEEMD算法分解
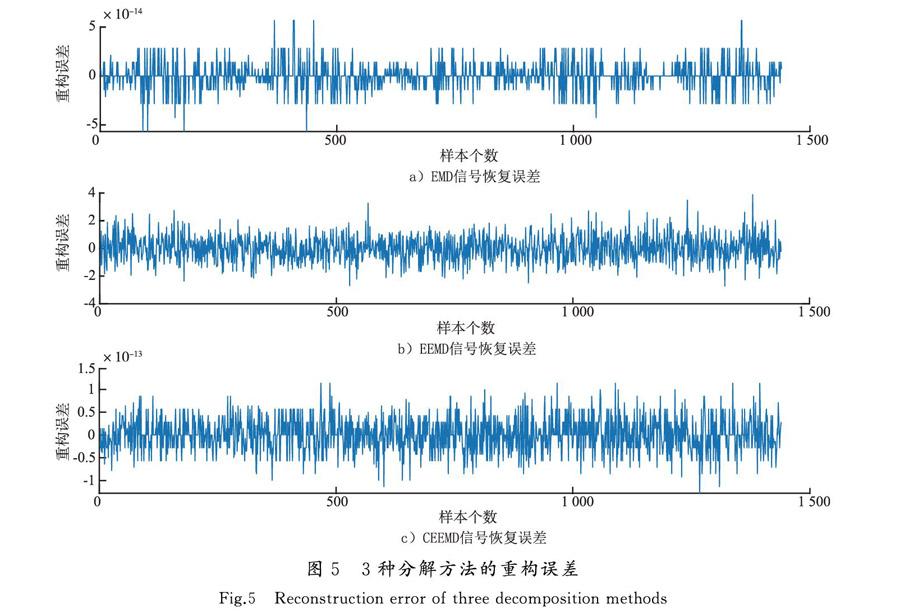
为了减少原始数据非稳定性和随机波动性对预测结果造成影响,需要选取更加稳定的分解算法。将原始交通流时间序列分别用3种分解算法进行分解重构,比较各个方法的优劣。3种方法分解重构后的误差见图5。
由图5可以看出,EMD分解算法在分解重构过程中不可避免地出现模态重叠现象;EEMD算法通过加入白噪声,可以有效消除模态重叠现象,但误差明显增大;CEEMD算法既可以消除模态混叠现象,又可以使重构后的误差恢复到原来的数量级别,为后续交通流数据分解提供了有力保障。
为了获取更加稳定的模态分量序列,在对原始交通流时间序列用CEEMD算法分解过程中,将添加到每组的白噪声幅度H设置为0.1,将集成适应对数N设置为100。根据CEEMD算法的自适应特性,将原始交通流时间序列分解为10组IMF分量和1组残余量,分解效果如图6所示。
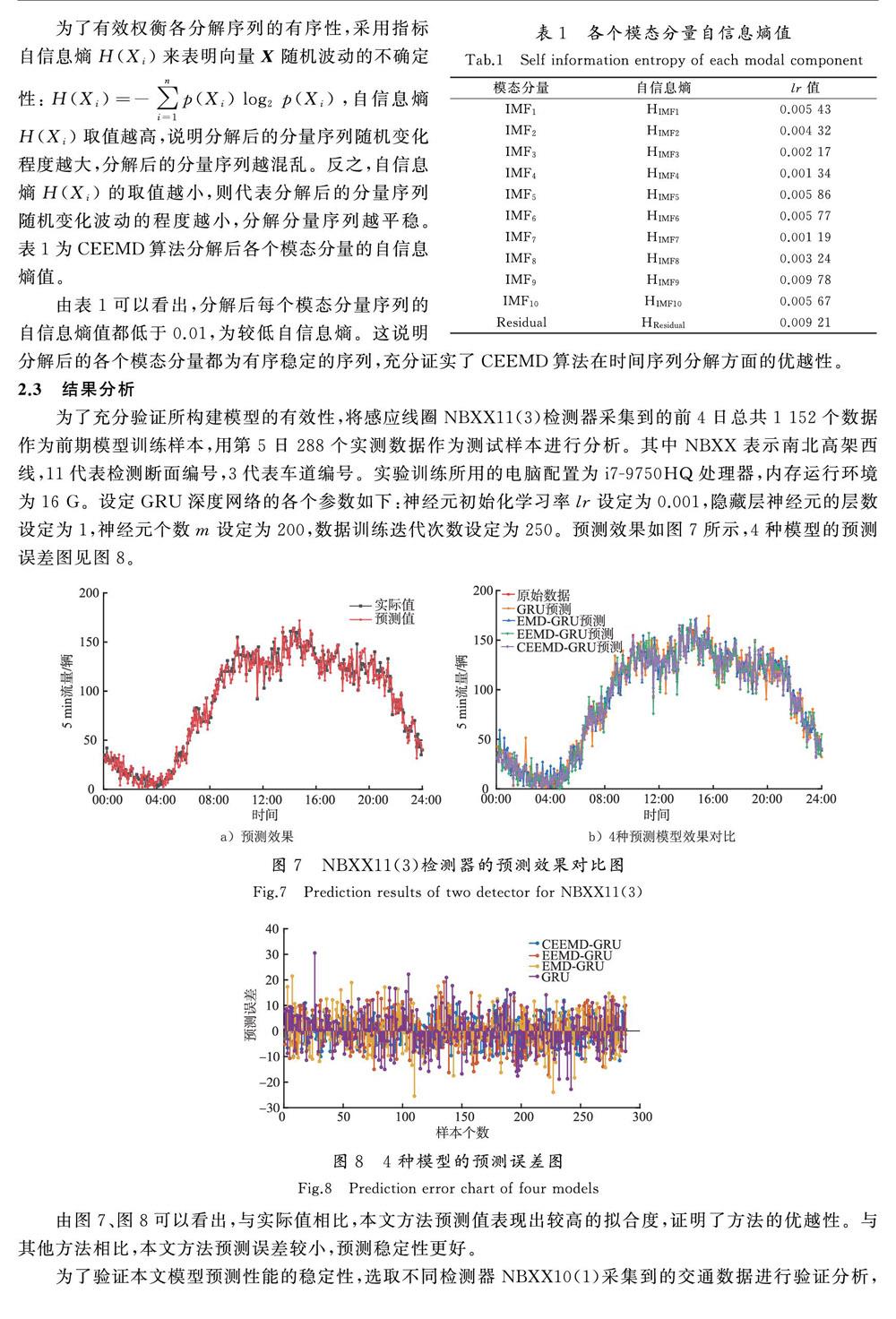
为了有效权衡各分解序列的有序性,采用指标自信息熵H(Xi)來表明向量X随机波动的不确定性:H(Xi)=-∑ni=1p(Xi)log2p(Xi),自信息熵H(Xi)取值越高,说明分解后的分量序列随机变化程度越大,分解后的分量序列越混乱。反之,自信息熵H(Xi)的取值越小,则代表分解后的分量序列随机变化波动的程度越小,分解分量序列越平稳。表1为CEEMD算法分解后各个模态分量的自信息熵值。
由表1可以看出,分解后每个模态分量序列的自信息熵值都低于0.01,为较低自信息熵。这说明分解后的各个模态分量都为有序稳定的序列,充分证实了CEEMD算法在时间序列分解方面的优越性。
2.3 结果分析
为了充分验证所构建模型的有效性,将感应线圈NBXX11(3)检测器采集到的前4日总共1 152个数据作为前期模型训练样本,用第5日288个实测数据作为测试样本进行分析。其中NBXX表示南北高架西线,11代表检测断面编号,3代表车道编号。实验训练所用的电脑配置为i7-9750HQ处理器,内存运行环境为16 G。设定GRU深度网络的各个参数如下:神经元初始化学习率lr设定为0.001,隐藏层神经元的层数设定为1,神经元个数m设定为200,数据训练迭代次数设定为250。预测效果如图7所示,4种模型的预测误差图见图8。
由图7、图8可以看出,与实际值相比,本文方法预测值表现出较高的拟合度,证明了方法的优越性。与其他方法相比,本文方法预测误差较小,预测稳定性更好。
为了验证本文模型预测性能的稳定性,选取不同检测器NBXX10(1)采集到的交通数据进行验证分析,其中NBXX表示南北高架西线,10代表检测断面编号,1代表车道编号,结果如图9所示。
由图9可以看出,在其他地点交通流预测中,本文预测方法同样表现出较高的准确度,再次验证了本文方法具有较高的预测性能。与其他方法相比,本文方法在预测方面具有更高的稳定性和较强的泛化能力。为了能够与其他预测方法进行直观比较,采用平均绝对误差(MAE)、平均绝对百分比误差(MAPE)和均方根误差(RMSE)3个指标进行分析评价,MAE=1n∑ni=1yi-y^i ,MAPE=1n∑ni=1yi-y^iyi×100%,RMSE=1n∑ni=1yi-y^i2。其中:yi表示i时刻的实际值;y^i表示i时刻的预测值;n为样本数。4种预测方法3项指标数值对比情况见表2和表3。
由表2和表3 可以看出,CEEMD-GRU模型在这3个指标评价中都表现出较高的性能。MAE值分别为5.89和6.01,MAPE值分别为9.52%和9.67%,RMSE值分别为5.81和5.91,较其他3种方法都有了较大提升,平均预测精度分别提升了33.4%,25.6%和18.3%。
3 结 语
1)為了提高交通流预测精度,给出行者提供一个更为合理、准确的出行路径,提出了CEEMD-GRU组合模型的快速路短时交通流预测方法。利用CEEMD算法对原始交通流数据进行多尺度分解,大幅度降低了交通流时间序列数据非平稳性对预测结果产生的影响,数据处理性能更为有效。
2)经过多次实例验证和对比分析,CEEMD-GRU组合模型在快速路短时交通流预测中具有较强的预测性能和泛化能力,能够满足短时交通流预测精度的要求,为快速路短时交通流预测提供理论参考和方法依据。
现实生活中出行者更希望得到出行时间内的交通流的动态信息,精确的单步交通流预测还是无法满足人们的出行要求。在本文研究的基础上,下一步还需在多尺度分解下多步交通流预测方面进行更为深入的研究。
参考文献/References:
[1] 王晓全,邵春福,尹超英,等.基于ARIMA-GARCH-M模型的短时交通流预测方法[J].北京交通大学学报,2018,42(4):79-84.
WANG Xiaoquan,SHAO Chunfu,YIN Chaoying,et al.Short term traffic flow forecasting method based on ARIMA-GARCH-M model[J].Journal of Beijing Jiaotong University,2018,42(4):79-84.
[2] 郭海峰,方良君,俞立.基于模糊卡尔曼滤波的短时交通流量预测方法[J].浙江工业大学学报,2013,41(2):218-221.
GUO Haifeng,FANG Liangjun,YU Li.A short-term traffic flow prediction model based on fuzzy Kalman filtering[J].Journal of Zhejiang University of Technology,2013,41(2):218-221.
[3] 傅成红,杨书敏,张阳.改进支持向量回归机的短时交通流预测[J].交通运输系统工程与信息,2019,19(4):130-134.
FU Chenghong,YANG Shumin,ZHANG Yang.Promoted short-term traffic flow prediction model based on deep learning and support vector regression[J].Journal of Transportation Systems Engineering and Information Technology,2019,19(4):130-134.
[4] ZHANG W B,YU Y H,QI Y,et al.Short-term traffic flow prediction based on spatio-temporal analysis and CNN deep learning[J].Transportmetrica A:Transport Science,2019,15(2):1688-1711.
[5] XIE Y C,ZHANG Y L,YE Z R.Short-term traffic volume forecasting using Kalman filter with discrete wavelet decomposition[J].Computer-Aided Civil and Infrastructure Engineering,2007,22(5):326-334.
[6] 谭满春,李英俊,徐建闽.基于小波消噪的ARIMA与SVM组合交通流预测[J].公路交通科技,2009,26(7):127-132.
TAN Manchun,LI Yingjun,XU Jianmin.A hybrid ARIMA and SVM model for traffic flow prediction based on wavelet denoising[J].Journal of Highway andTransportation Research and Development,2009,26(7):127-132.
[7] WEI Y,CHEN M C.Forecasting the short-term metro passenger flow with empirical mode decomposition and neural networks[J].Transportation Research Part C:Emerging Technologies,2012,21(1):148-162.
[8] YANG H F,CHEN Y P P.Hybrid deep learning and empirical mode decomposition model for time series applications[J].Expert Systems with Applications,2019,120:128-138.
[9] 陆文琦,芮一康,冉斌,等.智能网联环境下基于混合深度学习的交通流预测模型[J].交通运输系统工程与信息,2020,20(3):47-53.
LU Wenqi,RUI Yikang,RAN Bin,et al.Traffic flow prediction based on hybrid deep learning under connected and automated vehicle environment[J].Journal of Transportation Systems Engineering and Information Technology,2020,20(3):47-53.
[10]LI L C,QU X,ZHANG J,et al.Travel time prediction for highway network based on the ensemble empirical mode decomposition and random vector functional link network[J].Applied Soft Computing,2018,73:921-932.
[11]MA X L,TAO Z M,WANG Y H,et al.Long short-term memory neural network for traffic speed prediction using remote microwave sensor data[J].Transportation Research Part C:Emerging Technologies,2015,54:187-197.
[12]TIAN Y X,PAN L.Predicting short-term traffic flow by long short-term memory recurrent neural network[C]//2015 IEEE International Conference on Smart City/SocialCom/SustainCom.Chengdu:IEEE,2015:153-158.
[13]FU R,ZHANG Z,LI L.Using LSTM and GRU neural network methods for traffic flow prediction[C]//2016 31st Youth Academic Annual Conference of Chinese Association of Automation(YAC).Wuhan:IEEE,2016:324-328.
[14]罗向龙,李丹阳,杨彧,等.基于KNN-LSTM的短时交通流预测[J].北京工业大学学报,2018,44(12):1521-1527.
LUO Xianglong,LI Danyang,YANG Yu,et al.Short-term traffic flow prediction based on KNN-LSTM[J].Journal of Beijing University of Technology,2018,44(12):1521-1527.
[15]于德新,邱实,周户星,等.基于GRU-RNN模型的交叉口短时交通流预测研究[J].公路工程,2020,45(4):109-114.
YU Dexin,QIU Shi,ZHOU Huxing,et al.Research on short-term traffic flow prediction of intersections based on GRU-RNN model[J].Highway Engineering,2020,45(4):109-114.
[16]HUANG N E,SHEN Z,LONG S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society A:Mathmatical,Physical and Engineering Sciences,1998,454:903-995.
[17]WU Z H,HUANG N E.Ensemble empirical mode decomposition:A noise-assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41.
[18]YEH J R,SHIEH J S,HUANG N E.Complementary ensemble empirical mode decomposition:A novel noise enhanced data analysis method[J].Advances in Adaptive Data Analysis,2010,2(2):135-156.
[19]HOCHREITER S,SCHMIDHUBER J.Long short-term memory[J].Neural Computation,1997,9(8):1735-1780.
[20]譚雪,张小强.基于GRU深度网络的铁路短期货运量预测[J].铁道学报,2020,42(12):28-35.
TAN Xue,ZHANG Xiaoqiang.GRU deep neural network based short-term railway freight demand forecasting[J].Journal of the China Railway Society,2020,42(12):28-35.

