粒子群优化BP-PID的矿井提升机调速系统

赵仕艳，谢子殿，丁康康，崔含晴

(黑龙江科技大学 电气与控制工程学院，黑龙江 哈尔滨 150022)

矿井提升机是矿山开采和生产过程中的主要设备，其运行的安全性和高效性与煤矿经济效益息息相关。目前，我国煤矿企业中应用的提升系统主要有直流调速和交流调速两大类。直流调速性能存在电刷和换向器故障多以及结构和制造工艺复杂等问题，已逐渐被交流变频调速系统所代替[1-4]。在现实应用中，电机由于本身结构系统的复杂性，传统比例积分微分(Proportion Integration Differentiation，PID)控制器在电机调速系统应用时有速度超调大且转矩和磁链脉动大的缺点，导致调速控制系统难以达到预期效果。近年来，新型智能控制器在电机调速领域得到了广泛应用，如文献[5]中利用基于误差反向传播(Back Propagation，BP)算法的神经网络建立开关磁阻电机转矩模型的方法抑制转矩脉动。文献[6]利用滑膜控制方式解决了传统直接转矩(Direct Torque Control，DTC)电磁转矩脉动大、转速响应慢等问题。文献[7]将小波神经网络应用在感应电机DTC控制中以克服传统DTC转矩和磁链脉动大的缺点。但是，BP神经网络控制器在应用时存在收敛速度慢、学习效率低以及对参数过于敏感等缺点[8-11]，易导致网络陷入局部最优解。

本文研究的是利用粒子群优化算法(Particle Sawrm Optimization,PSO)收敛速度快和全局最优特性优化神经网络权值，在神经网络中设计收敛因子的方式提高网络的收敛性，以期共同改善矿井提升机调速系统特性。

1 电机侧控制策略设计

提升机的运转过程中包括加速、匀速、减速、爬行4个阶段，其中高速稳速运行是其主要的运行阶段。如图1所示，矿井提升机变频调速控制系统中的电机侧变流器采用神经网络直接转矩控制方式控制电机转速；网侧变流器为直流侧提供稳定电压。文中仅对电机侧变流器的控制策略进行研究。

图1 提升机控制系统结构图Figure 1. Control system structure of mine hoist

转速调节是提升机控制系统的主要核心部分。实际应用中，要求提升机分别能在超同步区间和亚同步区间高速稳定运行。转矩和磁链是调速系统中两个重要的参数，传统的PID控制器存在磁链和转矩脉动大的缺点，给电机带来如机械抖动、电机老化和过热等一系列问题，故常用神经网络来优化传统的PID控制算法。但BP神经网络在进行稳定学习时要求的学习率η较小，学习过程收敛速度慢。稳速学习时距离最优点的距离可表示为式(1)，只要|1-ητi|<1，则当n为无穷时，γi(n)等于0；若η较小，则1-ητi较大，降低了收敛速度。

γi(n)=(1-ητi)nγi(0)

(1)

式中，γi(n)为稳速学习距离最优点的距离；η为学习效率；τi为特征值。

本文设计两种方法来共同改善收敛速度慢和容易陷入局部最小的问题，即利用改进的粒子群算法优化神经网络权值并设计BP神经网络算法中的收敛因子改善调速系统性能。矿井提升机调速控制系统结构如图2所示。

图2 提升机调速控制系统结构图Figure 2. System’s structure of hoist’s speed regulation

2 粒子群优化算法

2.1 基本粒子群算法

粒子群算法具有很强的通用性，优化目标函数时只需要依据适应度函数，即可通过粒子的速度和位置更新公式进行更新来优化函数[12-15]。在D维搜索空间内，一个群体包N个粒子，记作X=[x1,…,xN]；粒子i的位置变化率vi=[vi1,…,vid]，其位置记作xi=[xi1,…,xid]，其中i=1,2,…,N；粒子i到当前迭代为止自身发现的最优位置记作pi=[pi1,…,pid]，到当前迭代为止全部粒子发现的最优位置记为pg=[pg1,…,pgd]。在找到这两个值之后，粒子速度和位置通过下列计算式更新。

(2)

(3)

式中，ω是惯性权重；vid和xid分别为粒子的速度和位置；pi和pg分别为自身和全局最优位置；c1和c2为学习因子；r1和r2为[0,1]的随机数。

2.2 改进粒子群算法

为提高粒子对自身和全局环境认知能力，并抑制局部极值的产生，本文对粒子群的惯性权重和加速因子参数进行改进。较大的惯性权值有利于全局搜索，较小的惯性权值则更利于局部搜索，而两个加速因子c1和c2分别代表了粒子自身和社会群体经验学习的权重[16-17]。在迭代初期，应尽可能的扩大搜索范围，且以自身学习为主，则惯性权重和自身经验学习因子较大；相反在迭代后期，接近于全局最优解，应更加精确局部的搜索全局最优解。此时则惯性权重和自身经验学习因子较小，社会群体经验学习较大。提出线性变化学习因子，正弦递减惯性权重参数，其操作表达式如下

(4)

(5)

(6)

式中，c1start、c1end为c1的起始值和最终值；c2start、c2end为c2的起始值和最终值；ωstart、ωend为ω的起始值和最终值；t、T分别为当前迭代值和最大迭代值。

3 神经网络PID控制器

3.1 基本神经网络控制原理

传统的PID由于比例、积分和微分3个系数固定不变，故无法实时调整参数的数值，系统的控制效果不理想，电机调速系统中会有很大的超调量且响应时间较慢。传统PID的增量式表达式为

△u(k)=KP△e(k)+KIe(k)+

KD(△e(k)-△e(k-1))

(7)

式中，KP、KI、KD分别为比例、积分、微分系数；e(k)为控制系统误差。

神经网络算法系统结构图如图3所示，该系统采用3层结构，通过不断调节输入层和输出层的权值得到PID参数的最佳组合。隐含层和输出层的激励函数分别采用双曲正切函数和非负的Sigmoid函数。

图3 神经网络结构图Figure 3. Structure of neural network

隐含层第i个神经元的输入和输出

(8)

vi=fi(ui)

(9)

式中，xm为输入层第m个神经元的输入；ui为隐含层第i个神经元的输入；ωmi为输入层加权系数；vi为隐含层第i个神经元的输出；fi(ui)为隐含层激励函数。

输出层第j个神经元的输入和输出为

(10)

yj=gj(uj)

(11)

式中，uj为输出层第j个神经元的输入；ωij为隐含层加权系数；yj为输出层第j个神经元的输出；gi(uj)为输出层激励函数。

3.2 改进神经网络算法

神经网络最突出的缺点是收敛速度慢和极易陷入局部最小值。因此本文提出在神经网络输出层加入收敛系数λ来提高稳速学习时的收敛速度。在稳定学习时，通过增大收敛系数增加PID控制器的控制量输出来扩大误差值，使控制量跳出局部最小的调节范围。收敛系数采用呈余弦函数增加

yj=λgj(uj)

(12)

(13)

式中，λstart、λend为λ的起始值和最终值。

由于该控制算法应用到了电机的调速系统，控制的是电机的电磁转矩，稳速调节阶段转矩输出值极小，转速上升缓慢。因此，文中通过调节收敛系数λ增大转矩值以加快转速上升速度。

3.3 PSO-BPNN-PID实现过程

将粒子群算法优化神经网络控制算法过程如下：

步骤1BP神经网络结构及粒子群初始化。网络的结构根据控制对象进行设计，PID控制器则采用三输入三输出结构，考虑到控制的效果及训练速度，将隐含层节点数设置为7；λ起始值和最终值设为1和2。粒子群c1起始值和最终值分别设为2和0.5；c2起始值和最终值分别设为0.5和2；ω起始值和最终值分别设为0.9和0.4，粒子数目取30；

步骤2确认粒子的模型并对权值编码。采用改进的粒子群算法更新神经网络的权值，粒子的维数对应神经网络的权值个数，将粒子位置与神经网络的权值一一对应。神经网络采用3-7-3结构，则粒子的维数为42，粒子位置为

(14)

步骤3计算粒子群的适应度。适应度函数为

(15)

步骤4计算个体与全局最优值。对个体与全局适应度进行对比，选取最优的个体极值与全局极值。

步骤5粒子速度和位置更新，更新神经网络的权值；

步骤6计算神经网络输出层，并计算出控制量u(k)；

步骤7判断是否达到所要求的适应度或最大迭代次数，输出最优解，若未满足条件则返回步骤3。

4 系统仿真结果

搭建矿井提升机调速系统的仿真模型，网侧直流电源udc=600 V，磁链给定值为1。电机主要参数为：额定功率Pn=600 kW，定子相电压Us=380 V，定子电阻Rs=0.02 Ω，定子漏感Ls=0.5 mH，转子电阻Rr=0.02 Ω，定子漏感Lr=0.5 mH，互感Lm=0.5 mH，极对数p=2，额定转速nN=1 490 r·min-1，电机转动惯量J=20 kg.m2。

4.1 亚同步运行区间

对电机在亚同步区间进行仿真分析，对比POS-BP-PID、BP-PID和传统PID控制器对电机控制效果，仿真条件如下：0 s时初始给定转速为1 300 r·min-1，在5 s时将速度给定到200 r·min-1，仿真时长为10 s，电机转速、电磁转矩分别如图4、图5和图6所示。

图4 亚同步区间3种控制器下电机转速Figure 4. Rotor’s speed of three controllers in sub-synchronous

(a)

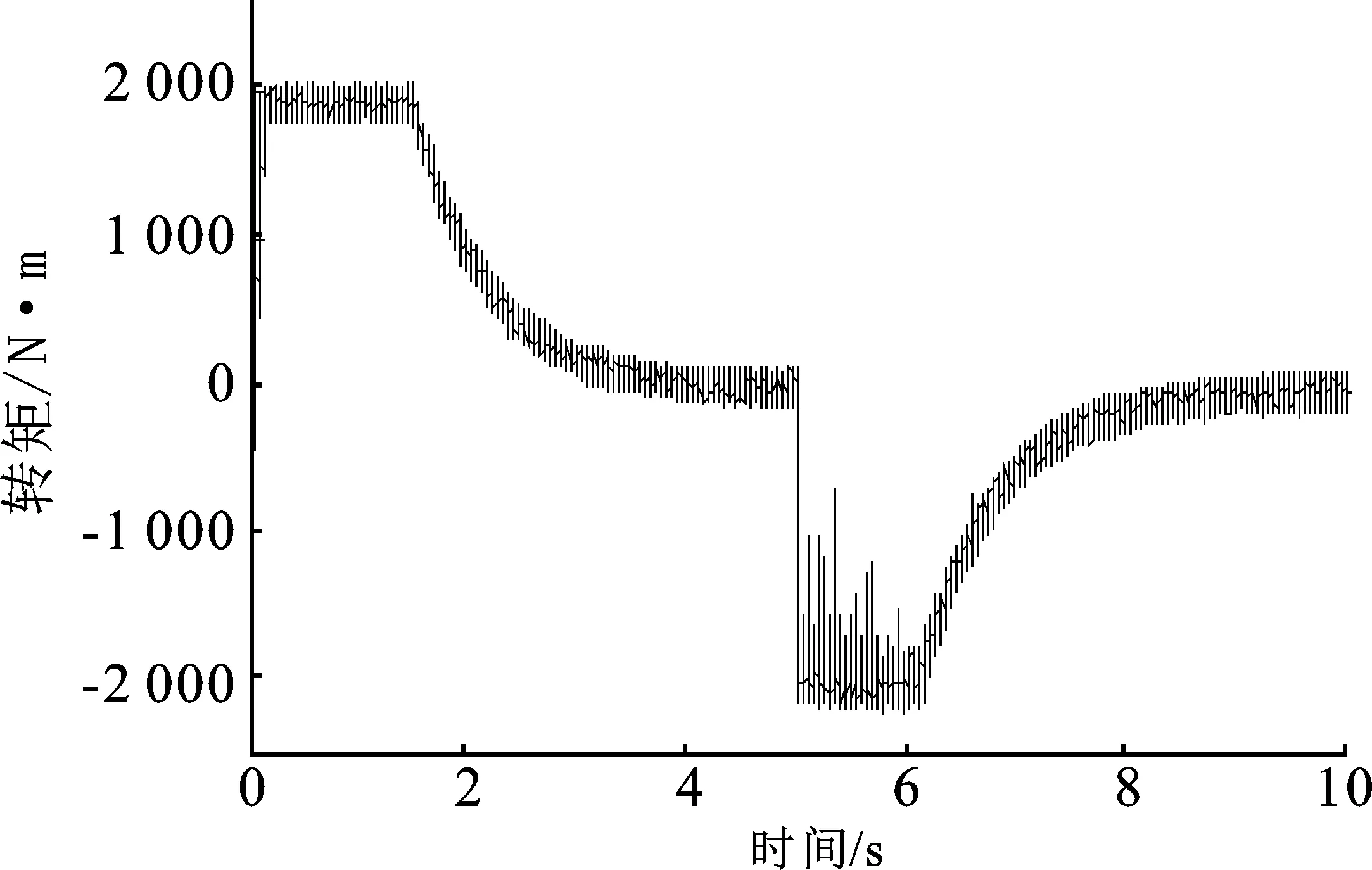
(b)

(c)图5 亚同步区间电机转矩(a)POS-BP-PID控制器(b)BP-PID控制器(c)传统PID控制器Figure 5. Rotor’s torque in sub-synchronous (a) POS-BP-PID controller (b) BP-PID controller (c) Traditional PID controller

(a)

(b)

(c)图6 亚同步区间电机转子磁链(a)POS-BP-PID控制器(b)BP-PID控制器(c)传统PID控制器Figure 6. Rotor’s flux in sub-synchronous (a) POS-BP-PID controller (b) BP-PID controller (c) Traditional PID controller

在亚同步运行区间，由进入稳速调节交界处展开图可知，传统PID控制器在进入稳速调节交界处速度有超调且波动，其它两种控制器无超调和波动。与 BP-PID控制器相比，粒子群优化后控制器转速在加速后稳速调节时响应速度更快， 到达给定速度响应时间为2.5 s，而BP-PID控制器响应时间则为4.9 s，响应速度提高48.98%；转速在减速后稳速调节时响应速度更快，到达给定速度响应时间仅为7.83 s，而神经网络控制器到达给定速度响应时间为9.2 s，响应速度提高32.62%。

电机在亚同步运行期间，粒子群优化后的控制器与神经网络PID控制器相比，转矩在加速和减速后稳速调节时响应速度更快，脉动小于250 N·m。在减速阶段，神经网络控制器转矩脉动更大即超过1 000 N·m，而传统的PID控制器转矩脉动约为450 N·m，在进入稳速调节交界处转矩有波动。

对于电机转子磁链脉动，传统PID控制器与其它两种控制器相比，其脉动较大且大小约为0.1，其它两种控制器磁链脉动在0.03左右，脉动降低了70%。

4.2 超同步运行区间

在超同步区间进行仿真分析，对比3种控制器对电机控制效果，仿真条件为：0 s时初始给定转速为2 000 r·min-1，在8 s时刻跃变到200 r·min-1，仿真时长为15 s，电机转速和转矩曲线分别如图7和图8所示。

图7 超同步区间3种控制器下电机转速Figure 7. Rotor’s speed of three controllers in super-synchronous

(a)

(b)

(c)图8 超同步区间电机转矩(a)POS-BP-PID控制器(b)BP-PID控制器(c)传统PID控制器Figure 8. Rotor’s torque in super-synchronous (a) POS-BP-PID controller (b) BP-PID controller (c) Traditional PID controller

在超同步运行区间，由进入稳速调节交界处展开图可知，传统PID控制器在进入稳速调节交界处速度有超调且波动，其它两种控制器无超调和波动。粒子群优化后的控制器与神经网络PID控制器相比，转速在加速后稳速调节时响应速度的响应时间为3.85 s，而神经网络控制器到达给定速度响应时间为6.1 s，响应速度提高36.89%；转速在减速后稳速调节时响应速度更快，到达给定速度的响应时间为11.5 s，而神经网络控制器到达给定速度响应时间为13.5 s，响应速度提高了36.36%。

电机在超同步运行期间，粒子群优化后的控制器与神经网络PID控制器相比，在加速后和减速后稳速调节期间转矩响应速度更快。但在减速阶段，神经网络控制器转矩脉动更大，接近2 000 N·m，传统PID控制器转矩脉动为450 N·m左右，在进入稳速调节交界处转矩有波动。

4.3 仿真总结

经上述仿真分析，将3种控制器所得到的电机参数进行对比，如表1所示。相较其它控制器电机调速系统，粒子群优化的神经网络控制器控制效果的稳定性和鲁棒性得到了较大幅度提高。

表1 3种控制器参数对比Table 1. Comparison of parameters of three controllers

5 结束语

本研究结合矿井提升机运行特点，建立了绕线式异步电机在粒子群优化神经网络PID控制的直接转矩模型。本模型既考虑了矿井提升机亚同步区间，又考虑了超同步区间运行工作状态，通过MATLAB/Simulink仿真验证了绕线式异步电机转子变频调速中神经网络PID控制的可行性。仿真结果表明：(1)矿井提升机在POS-BP-PID控制器下，较传统PID控制器电机转子磁链脉动减少了70%，且电磁转矩脉动减少了44.44%；(2)矿井提升机在POS-BP-PID控制器下，电机转速无超调且无脉动，较BP-PID控制器在亚同步和超同步运行区间运行时转速响应速度都提高了30%以上；(3)新方法能满足矿井提升机在亚同步区间和超同步区间的运行要求，并提高了系统的稳定性和抗干扰性。