政府直接补贴风投机构政策的效果分析及改进建议

陈宗义，卞 晨

(1.齐鲁工业大学 金融学院，济南 250100；2.东北大学 工商管理学院，沈阳 110000)

1 研究背景

近年来，多地政府直接补贴风投机构的现象屡见不鲜。2014年，北京市出台《中关村国家自主创新示范区天使投资和创业投资支持资金管理办法》，对天使投资和创业投资分别按照不高于上年度投资额的15%和10%进行直接补贴，其中单个天使投资和创业投资项目的补贴上限分别为45万和100万，单个天使投资和创业投资机构的补贴上限分别为150万和200万。2015年，天津市出台《天使投资引导资金管理暂行办法》，按照天使投资机构当年实际投资额的10%进行直接补贴，单个项目和单个机构补贴上限分别为50万和200万。2018年广州市海珠区也出台类似政策，对风险投资机构按其对地区经济社会发展贡献给予5年的经营贡献奖励，前3年奖励90%，后2年奖励50%。伴随而来，关于政府直接补贴风投机构的话题讨论也逐渐升温，其中反对意见聚焦于政策合理性与有效性两个方面。

反对者认为政府将纳税人的钱支付给风投机构并不合理。反对者坚称风投机构开展投资业务属于一般性商业活动，盈亏与否本就由市场决定，即使亏损也不应获得财政补贴。然而，从法理上讲，各级政府运用财政资金对风投机构进行补贴具有合法性。我国《宪法》《科学技术进步法》和《促进科技成果转化法》赋予各级政府“通过财政资金投入为科学技术研发和应用提供良好的外部环境”的权力；从履行权力形式上讲，对风险投资进行政府补贴是以私法化的方式履行其公法职责，既是直接的物质给付，又属于间接的环境保障给付［1］。反对者认为政府补贴风投机构政策并非有效，即该政策并不能帮助创业企业获得更多融资。某些学者质疑相关政策的有效性，同时担心政府补贴风投机构可能会引发寻租行为和逆向选择，反而会吸引那些不诚信或能力差的风投机构恶意套取补贴［2-3］。也有学者认为，政府直接补贴风投机构具有政策有效性，刘志伟等［4］建立了一个包含风险投资者和创业者两方的四阶段完美信息动态博弈模型，基于信息不对称和双边道德风险条件研究最佳契约设计，研究发现，政府的直接补贴政策，即当风险投资者遭受损失时可以通过申请政府补贴而获得部分补偿，在促进风险资本供给增加的同时还能提升创业企业对风险资本的需求。

相关领域国内文献数量较少，即使扩大范围来看，研究政府政策对风投机构影响的国外文献也不多。根据目前所掌握的文献，国外政府主要通过放松风投市场准入［5］、促进股票市场发展［6-7］、针对风投机构的税收优惠［8-11］和强化公共研发投入等政策［12］来激励风投机构支持企业的创新活动，因此国外学者们也是围绕以上几种政策展开研究，而政府直接补贴风投机构的政策效果则尚未有研究涉及。

地方政府之所以被赋予制定并出台直接补贴风投机构政策的权力，其前提是能够为“科学技术研发和应用提供良好的外部环境”。换言之，相关政策必须要达到间接改善当地创业企业融资环境的目标，若直接补贴政策无助于实现此类目标，则其立法依据也就无法确立。因此，直接补贴政策合理性取决于其有效性，而探究政府直接补贴风投机构政策有效性就成为解决争论的关键。

相关研究或者仅停留于定性分析层次，未能明确经济现象背后的行为主体，也没有清晰界定行为主体间的利益关联，导致结论缺乏可信度；或者采用两方博弈分析的定量方法［4］，忽略了政府、风投机构和创业企业3类主体间决策互相影响的客观事实。此外，不论研究结论是否能支持政府直接补贴政策的有效性，都应找出其内在机理，而现有研究却未曾触及。鉴于此，本文首次将三方演化博弈方法引入相关研究以贴合现实，构建包含有限理性的政府、创业企业和风投机构三方的非合作演化博弈模型，并分析其演化稳定均衡，同时尝试寻找具有解释力的内在机理以阐述政府直接补贴政策为何有效或非有效，旨在为我国风投行业健康发展提供坚实的政策依据。

2 三方演化博弈模型的设计理念与构建

要建立包含政府、创业企业和风投机构三方演化博弈模型，首先需要设计三方的支付函数。现对三方支付函数的设计理念加以阐释。

2.1 三方支付函数的设计理念

2.1.1 政府支付函数的设计理念 中短期内，由于不能排除某些干扰因素的存在，难以断定政府是否严格按照收益最大化原则来进行决策。例如，委托代理问题就属于典型的干扰因素。某位政府官员为追求任期内GDP高速增长或就业率明显改善的政绩会忽视未来税基的增长。从长期来看，这些干扰在相当程度上会被纠偏。前任政府官员可以忽视税基增长，但继任官员以及之后再继任的官员面临同样宽松的财政资金约束是否会延续类似政策呢？因此，从长期来看，政府决策无法脱离收益最大化的基本考量，而税收收入减去直接补贴的差额则能够较好地体现这种最大化偏好。与此同时，演化博弈模型本来就更关注与分析有限理性参与方在长期过程中对最佳策略的试错性探求，所以政府支付函数暂定为税收收入与直接补贴的差额。

2.1.2 创业企业支付函数的设计理念 创业企业主要关注自身市场价值成长，同时需要向政府支付税金，创业企业的支付函数主要包括这两部分。对企业主而言，需要面对一种权衡：不引入风险投资而保留全部原始股份，这时企业市场价值增长相对滞后；引入风险投资，企业未来发展可能更有前景，却需要出让部分原始股份，不过具体出让份额可由企业主自由裁量。

2.1.3 风投机构支付函数的设计理念 政府给予直接补贴相当于额外增加了风投机构收益，是否必然会激励其扩大投资仍未可知，需要纳入整个支付函数才能确定。基于成本收益分析，风投机构的支付函数应至少包含3类要素：融资成本(融资规模×单位融资成本)、税收成本和投资创业企业股票之后再变现的预期收益(融资规模×单位预期投资收益)。单位融资成本和税率基本可视为外生给定，风投机构在较大程度上控制着融资规模与单位预期投资收益。单位预期投资收益看似完全外生给定，其实恰恰相反，风投机构在选择较高单位预期投资收益的投资项目方面具有相当大的主动性。同时，风投机构投资决策背后必然存在某些决定性影响因素，只有明确这些影响因素才能设计出风投机构支付函数。

风投机构投资影响因素的相关研究成果比较丰富，大致可以分为3类。①环境因素。地理因素［13-14］、市场环境［15］、当地创业水平［16］、文化差异［17-18］、高铁网络出现［19］、制度差异［18，20］和政府招商力度［21］等都会影响风投机构的决策。②创业企业特质。创业者先前的行业经验和管理经验［22-23］、高管团队的人力资本特征［24］，以及创业企业与风投机构团队成员间是否存在紧密关系［25-28］等，都会影响风投机构的策略选择。

综合上述各类影响因素来看，风投机构的专业知识能力无疑最为核心。一方面，第一类专业知识能力——准确估值能力可以帮助风投机构发掘理想的投资对象；另一方面，在对某创业企业投资之前，风投机构肯定也要对自身第二类专业知识能力——资源整合能力进行内部评估：将创业企业所对应环境要素和目标企业特质等信息材料纳入考量，以评价自身对各种内外部资源的整体驾驭能力，而评估结果的具体数值基本可以视为某项目估值的预期可实现程度。这一评估过程势必会影响最终的投资决策，而其他几类影响因素也都深深嵌入风投机构的资源整合能力。

由此可以建立风投机构支付函数的基本框架：①这里并未对M1进行过多设定，包括M1和M0之间具体的数量关系以及M1与准确估值能力之间的关系(M1可以视为准确估值能力的函数)。原因在于下面分析演化平衡点稳定性条件时，M1被计算过程自动约略，并不对演化稳定均衡点的形成构成任何影响。融资成本，由当时金融市场供给状况决定；②投资创业企业股票之后再变现的预期收益，由风投机构专业知识能力主导；③政府直接补贴政策，由政府财政政策决定。至于税收成本，由政府税收政策决定，但结合国内外对风投机构税收抵免政策情况，同时为简化分析，在下文论述时，假设政府全部豁免风投机构所应缴纳的利润所得税。

2.2 具体构建

市场上有政府、创业企业和风投机构3类行为主体，本文构建由政府、代表性创业企业和代表性风投机构所组成的三方演化博弈模型。为建立模型，首先提出下列假设。

假设1 政府为参与人1，创业企业为参与人2，风投机构为参与人3，且三方参与人均为有限理性。

假设2 三方参与人在当前时间点T0做出决策，且均会将未来时点T1的各自收益纳入决策约束，金融市场上时点T0到T1的平均利率为k且k＞0，则折现系数为

假设3 创业企业和风投机构洽谈融资合作时，风投机构会对创业企业未来市场价值进行评估，假定具体估值为M1，其含义为代表性创业企业在获得风险投资后，按照常规增长率推算企业将在未来时点T1所对应的市场价值。M1的确定主要依赖于风投机构的第一类专业知识能力——准确估值能力。此外，假设M1估值的预期可实现程度为θ。如上所述，θ的数值含义基本等同于风投机构对其所具备第二类专业知识能力——资源整合能力的评估水平。θ取值范围通常为0＜θ＜1，但在理论上也并不排除θ＞1的极端情况，即估值可以超额实现；若未获得融资，创业企业缓慢发展，则对未来时点T1的市场价值进行自我评估，具体估值为M0，且M1＞M0①。假设相关信息亦为政府所获悉。

假设4 政府对风投机构的投资行为采取从量补贴方式，即当风投机构不开展投资活动时不予补贴，与之相对应，政府在T1时点会获得来自创业企业缴纳的税收，t为税收系数，且0 ＜t＜ 1。当风投机构开展投资活动且与创业企业签订融资契约之后，政府的策略选择空间为α=(α1，α2)=(高额补贴，低额补贴)。政府会以1-x的概率对风投机构进行低额补贴，补贴比率为q且q＞0；政府以x的概率对风投机构进行高额补贴，补贴比率为q(1+c)，且0＜c＜1。与之相对应，政府在T1时点会获得来自创业企业缴纳的税收

假设5 创业企业的策略选择空间β=(β1，β2)=(强意愿融资，弱意愿融资)，且以y的概率选择强意愿融资，此时创业企业愿意出让a份额的股权，0＜a＜1。若创业企业与风投机构达成融资契约，则转让价格应为δaM1，δ为期权交易价格，表示风投机构能够以多少成本锁定创业企业在未来时点T1的单位市场价值，0＜δ＜1。δ可以视作由彼时金融市场所决定的外生变量。创业企业以1-y的概率选择弱意愿融资，此时创业企业愿意出让b份额的股权，0＜b＜1且b＜a。若创业企业与风投机构达成融资契约，则转让价格应为δbM1。

假设6 风投机构的策略选择空间γ=(γ1，γ2)=(同意投资，拒绝投资)，即风投机构以z的概率选择同意投资，此时风投机构会获得预期投资收益和政府补贴这两类收益。风投机构以1-z的概率选择拒绝投资，此时风投机构无法获得任何收益，但也因无须募集资金而不用支付任何成本。

假设7 风投机构无运营成本，且可以随时从金融市场募集所需资金，每单位募集资金使用成本等于金融市场上的平均利率k，且在T1时点支付。

根据上述支付函数设计理念与基本假设，可以得出三方博弈支付矩阵，具体如表1所示。

表1 三方博弈的支付矩阵Tab.1 Payment matrix of tripartite game

3 演化稳定均衡

3.1 演化过程均衡点的推导

在初始阶段，假设政府选择高额补贴的概率为x(0≤x≤1)，低额补贴的概率为1-x；创业企业选择强意愿融资的概率为y(0≤y≤1)，弱意愿融资的概率为1-y；风投机构同意投资的概率为z(0≤z≤1)，拒绝投资的概率为1-z。政府选择高额补贴和低额补贴的期望效用Ug、U-g及群体效用分别为

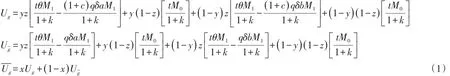
创业企业选择强意愿融资和弱意愿融资的期望效用Uc、Uc-及群体效用分别为

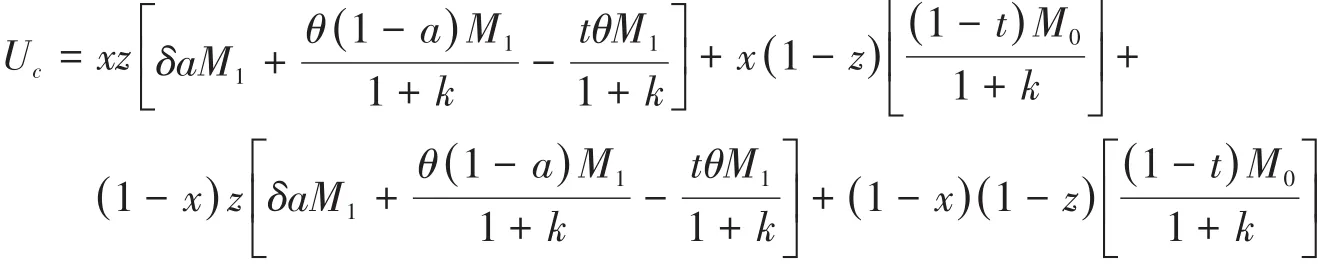
根据Malthusian方程，政府选取高额补贴策略的增长率与选择该策略所获得的效用与群体效用差成正比，故有

同理，可得创业企业与风投机构的复制动态方程。

由3个群体的复制动态方程可得三维动力系统(J)，如式(5)所示。

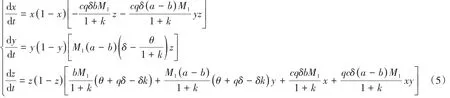
为简化计算，令

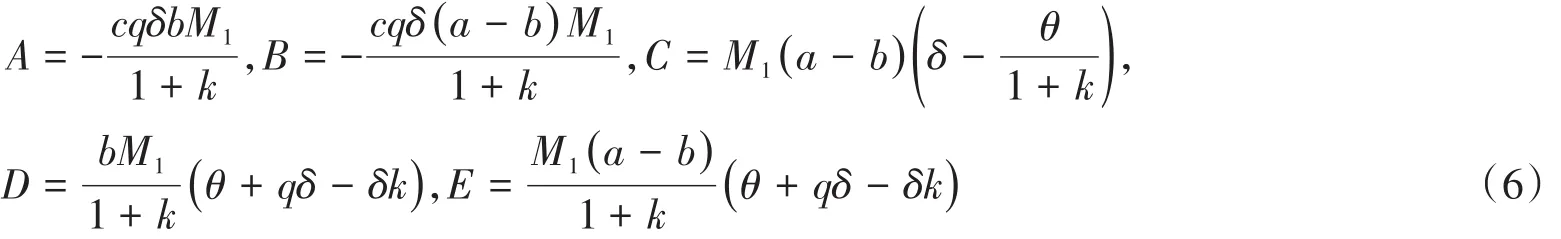
则变形后的(J)为

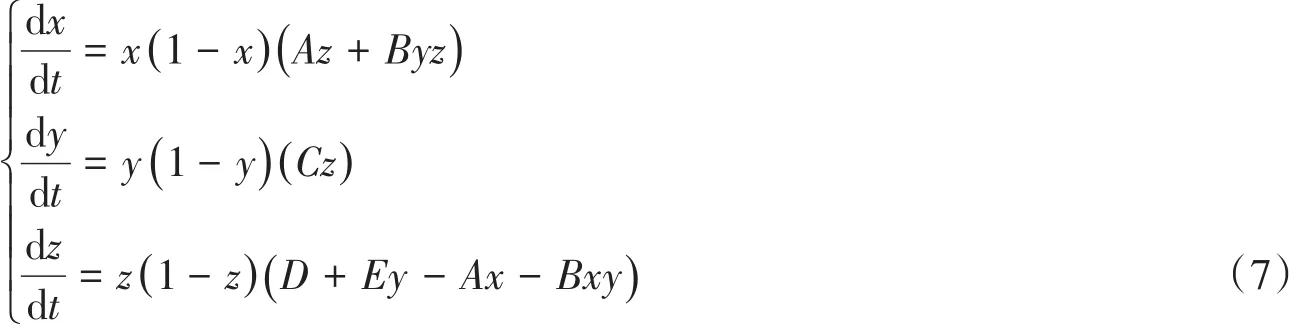
由复制动态系统可得到(0，0，0)、(0，0，1)、(0，1，0)、(1，0，0)、(1，1，0)、(1，0，1)、(0，1，1)、(1，1，1)8个局部均衡点。若演化博弈均衡是渐进稳定状态，则必是严格纳什均衡，而严格纳什均衡又属于纯策略均衡。因此，对于上述复制动态系统，只要讨论其在平衡点的稳定性即可。

3.2 平衡点的稳定性分析

系统(J)的雅克比矩阵为

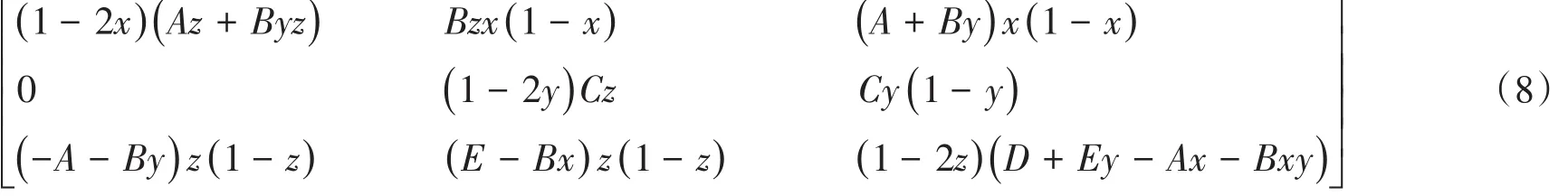
以点E2(0，0，1)与点E3(0，1，0)为例，讨论其满足渐进稳定状态的条件。

复制动态系统(J)在E2(0，0，1)处的雅克比矩阵为

矩阵的特征值为λ1=A，λ2=C，λ3=-D。

当A＜0，C＜0，-D＜0时，由李亚普洛夫渐进稳定性条件可知E1是渐进稳定的，此时E1即为汇；当A＞0，C＞0，-D＞0时，由李亚普洛夫稳定性条件可知E1是不稳定的，此时E1即为源；当A，C，-D中有一负两正或者一正两负时，由李亚普洛夫稳定性条件可知E1是不稳定的，此时E1为鞍点。

复制动态系统(J)在E3(0，1，0)处的雅克比矩阵为

矩阵的特征值为λ1=0，λ2=0，λ3=D+E。由于λ1=0，λ2=0，不满足李亚普洛夫稳定性条件，其稳定性不确定。接下来，本文将给出E1～E8能达到渐进稳定状态的具体条件，如表2和表3所示。

表2 系统(J)的平衡点及其特征值Tab.2 Equilibrium points and the eigenvalues of system(J)

表3 系统(J)的平衡点稳定性条件Tab.3 Equilibrium points’stability condition of system(J)

对条件①进一步整理可知，只须满足：

因为k+1＞k-q，故式(11)进一步整理为

即能保证E2(0，0，1)成为演化稳定点。

对条件②整理可知，只须满足：

进一步整理可得

即能保证E7(0，1，1)成为演化稳定点。

4 结论

4.1 政府直接补贴政策在长期中无效

首先，比较2个演化稳定均衡点所对应创业企业融资环境有何不同。点E2(0，0，1)，即政府、创业企业和风投机构策略组合(低额补贴，低意愿融资，同意投资)成为演化稳定均衡点时，创业企业的融资环境比较宽松和理想。创业企业融资意愿不强烈意味着企业仅面对较弱的融资约束，这种情况下创业者只须出让较少原始股份就能够获得来自风投机构的投资，显然这是比较理想的创业环境。点E7(0，1，1)，即政府、创业企业和风投机构策略组合(低额补贴，高意愿融资，同意投资)成为演化稳定均衡点时，创业企业的融资环境比较恶劣。创业企业对资金的渴求也昭示了企业正面临较强的融资约束，此时创业者虽然能获得风投机构投资但却需要出让更多原始股份。因此，当演化稳定均衡点从E2(0，0，1)转移至E7(0，1，1)时，意味着创业企业所面临的融资环境出现恶化；当演化稳定均衡点从E7(0，1，1)转移至E2(0，0，1)时，意味着创业企业所面对融资环境得到改善。

其次，讨论政府直接补贴政策可能会对演化稳定均衡点形成和转移造成的具体影响。对于政府而言，δ、k和θ均属于外生变量，其唯一能有效控制的变量只有直接补贴比率q。政府出台直接补贴政策就相当于将q值从0提升至某个正数，调整直接补贴政策其实就是调整q值。当式(12)得到满足，即1成立时，E2(0，0，1)肯定会成为唯一的演化稳定均衡点，政府无法通过调整q来进行干预，而且点E2(0，0，1)本就属于比较理想的创业环境，政府也没有必要通过出台以及调整直接补贴政策来加以干预；当满足式(14)，即1-q成立时，政府可以通过实施和调整直接补贴政策干预市场，但影响相当有限。因为政府通过干预q值只能改变不等式的右侧，即通过实施直接补贴政策拓展了风投机构的备选项目库，却无法改变不等式的左侧，所以直接补贴政策无力实现E7(0，1，1)至E2(0，0，1)的跨越，也就难以有效改善创业企业的融资环境。

综上所述，当满足式(12)时，政府没有能力也没有必要出台直接补贴政策来干预市场；当满足式(14)条件时，政府出台和调整直接补贴政策也无法有效改善创业企业所面对的融资环境。因此，在长期政策调整过程中，政府会逐渐意识到直接补贴政策无效，并出于追求利益最大化原则将最终放弃直接补贴政策。具体调整过程中允许各种试错路径的存在，例如高额补贴调整为低额补贴，再持续调低直接补贴比率，最终放弃直接补贴政策；或者低额补贴调整为高额补贴转而再调整为低额补贴，再持续调低直接补贴比率，最终放弃直接补贴政策；或者两种政策的反复切换后最终放弃直接补贴政策。

4.2 演化稳定均衡点的形成主要基于k与θ的协同变化

在符合式(12)和式(14)的前提下，结合实际情况令δ=0.1，q=0.1，考察k从0.1～0.9变化时θ变动对演化均衡点形成的影响，具体如表4所示。从表4可以看到，θ数值的变动对演化均衡点形成仍具有重要影响，但与此同时金融市场上时点T0到T1的平均利率k，其数值变动对演化均衡点形成也产生显著影响。点E2(0，0，1)代表创业企业拥有比较理想的融资环境，要令其成为演化稳定均衡点，则k与θ的赋值必须保持正向关联的协同变化。在k赋值较小时，对θ赋值要求也比较宽松；在k赋值较高时，对θ赋值要求也比较苛刻。例如：在k赋值为0.1时，要求θ＞0.11，即对风投机构的资源整合能力要求不必过高时就可以令E2(0，0，1)成为演化稳定均衡点。当k赋值为0.9时，则要求θ＞ 0.19，这说明点E2(0，0，1)达成演化稳定均衡状态的难度有可能已经呈几何倍数递增。

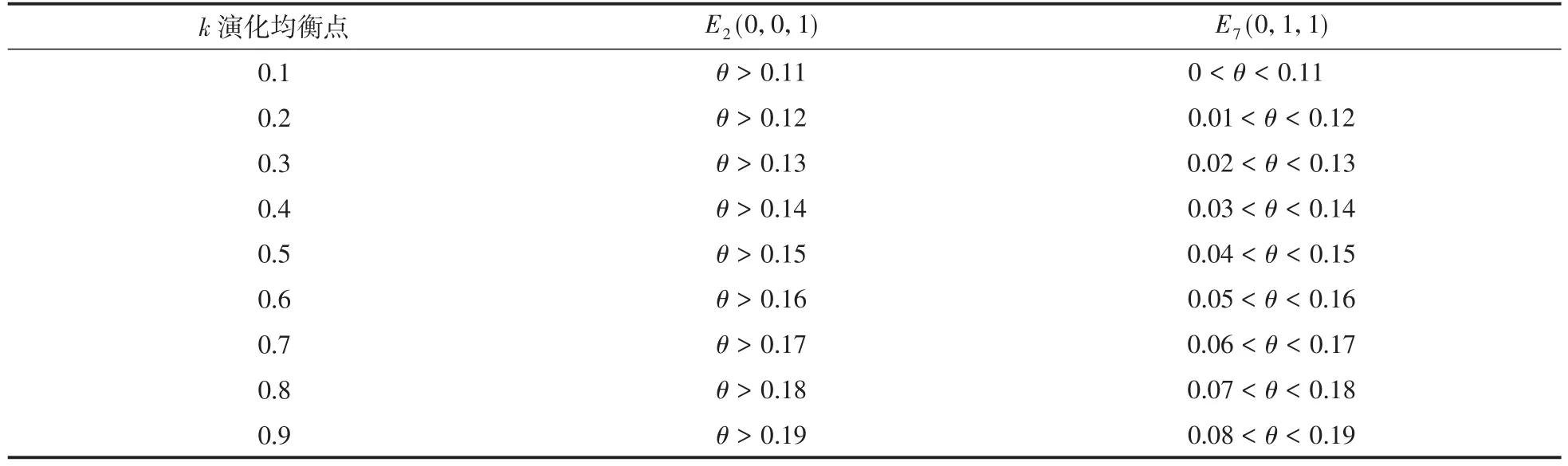
表4 k与θ协同变化条件下演化稳定均衡点的实现Tab.4 Realization of evolutionary stable equilibrium points under cooperative change ofkandθ

k与θ赋值正向协同变化背后的经济含义为：当金融市场利率水平较低时，风投机构具备较低的资源整合能力就容易营造出比较理想的创业融资环境；当金融市场利率水平较高时，只有风投机构具备较高的资源整合能力才能够营造出比较理想的创业融资环境。

5 政府直接补贴政策长期无效论的内在机理及现实证据

结论4.1是三方演化博弈模型的基本推论，有必要对其所蕴含的内在机理进行深度挖掘。

5.1 内在机理

“政府针对风投机构的直接补贴政策在长期中无效”是政府经过持续性策略调整，即不断尝试调整直接补贴比率，并在达成演化稳定均衡状态后形成的一种理性认知，此种认知终将导致政府放弃直接补贴政策。可以隐约感知到：政府每一次调整直接补贴政策，其背后应该具备大致相同的经济逻辑。若此经济逻辑不存在，则长期中政府持续的政策调整就会倾向于随机抉择，从而无法达成演化稳定均衡状态。如果某种经济逻辑能够影响政府直接补贴政策出台及其后续调整，则此经济逻辑即可被认定为政府直接补贴政策长期无效的内在机理。

本文认为，直接补贴政策缺乏政策粘性就是要找寻的经济逻辑。这里首先定义“政策粘性”。若直接补贴政策出台及其后续调整使得新进入和已进入的风投机构不会轻易选择离开，并持续在当地开展新的投资活动，则称其具备政策粘性。政策粘性容易引发某种聚集效应，并很有可能在多年后彻底改良当地创业企业的融资环境。缺乏政策粘性则指单凭直接补贴政策难以确保风投机构在当地持续开展投资活动。

如果直接补贴政策缺乏政策粘性，就说明其无法有效激励已获补贴的风投机构在当地开展更多投资活动。换言之，即使风投机构在当地进行投资决策背后依旧是市场因素，而非直接补贴政策发挥主导作用。如此，在长期政策调整过程中，政府会发现直接补贴政策无助于改善当地创业企业融资环境，即直接补贴政策在长期中无效。在回答政府直接补贴政策为何会缺乏政策粘性这个问题之前，需要重新审视一下式(12)即的经济含义。因为θ也代表着项目估值的预期可实现程度，而δ代表风投机构锁定未来每单位收益的成本，因此可以将视为风投资本的预期增值水平。例如：当θ=0.3且δ=0.1时值为3，这表明风投机构最初投入的1单位资本将增值为3单位。k为风投机构投资周期时点T0到T1时段的平均利率水平，k+1就可以看作金融市场上每单位资本经过T0到T1时段完成增值后的本息和，无非是从另外一个角度体现市场的平均利润。因此，式(12)经济含义可以理解为风投机构的资本增值水平超过了金融市场平均利润水平。

综上所述，不论以上哪类情况，政府出台及调整直接补贴政策均无法确保已获补贴风投机构更倾向于在当地开展投资活动，也就不可能达到改善当地创业企业融资环境的政策目标，从而可以确定缺乏政策粘性是政府直接补贴政策长期无效的内在机理。

5.2 数值模拟

为更加直观地展示本文的基本结论——政府直接补贴政策及其后续调整在长期中无效，下面将采取数值模拟方法进行推演。

风险投资项目一旦成功将会获得极高的收益。著名的以色列YOZMA投资计划，其成功项目的回报率就在10倍以上。在符合式(12)和式(14)的前提下，结合实际情况令δ=0.1和k=0.3，同时鉴于各地方政府对风投机构补贴比率一般不超过15%，现考察q在0～0.2范围内变化时，θ变动对演化均衡点的影响。特别地，当q值取0时，也表明政府未出台直接补贴政策。具体结果如表5所示。

表5主要传达了以下信息。①演化稳定均衡点E2(0，0，1)具体形成过程丝毫不受q变化的影响。已知δ=0.1，k=0.3，通过计算可知，当满足θ＞ 0.13时，式(12)必定满足，从而保证E2(0，0，1)成为演化稳定均衡点。对于政府来讲，唯一能有效控制的变量只有直接补贴比率q，而δ、k和θ均属于外生变量，只要保证θ＞0.13，即使q值在0～0.2范围内逐步变化，也不会改变演化稳定均衡点E2(0，0，1)的形成。②演化稳定均衡点E7(0，1，1)具体形成过程部分受到q变化的影响。当q值在0～0.2范围内逐步变化时，θ值下限也发生相应浮动，从0.03逐步过渡到0.01。这说明政府通过实施直接补贴政策相当于拓展风投机构的备选项目库，而调整q相当于修正风投机构备选项目库的范围。如前所述，点E7(0，1，1)所对应的创业企业融资环境不甚理想，但无论q值如何调整，也无法改变θ值的上限0.13。这表明政府无法通过出台和调整直接补贴政策来实现E7(0，1，1)至E2(0，0，1)的跨越。

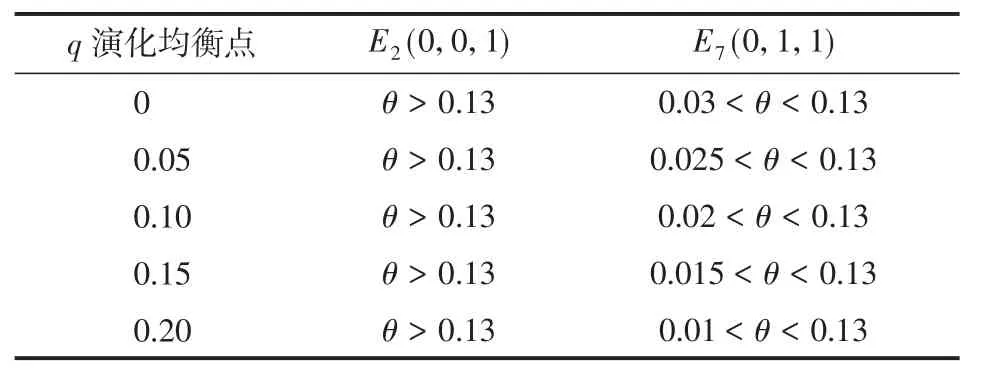
表5 q与θ协同变化条件下演化均衡点的实现Tab.5 Realization of evolutionary stable equilibrium points under cooperative change ofqandθ

为更直观地展现θ数值变动对演化均衡点形成所施加的重要影响，特别考察δ=0.1、k=0.3、q=0.1时，θ赋值分别为0.1和0.2时所对应的三方博弈的演化稳定走势。图1和图2演示了θ分别赋值为0.1和0.2时所对应三方博弈演化稳定均衡的形成态势。由图1可知，当θ赋值为0.1时，三方的演化稳定均衡点为E7(0，1，1)；由图2可知，当θ赋值为0.2时，三方的演化稳定均衡点为E2(0，0，1)。由此可知，θ在演化均衡点形成过程中确实发挥了关键作用，且当θ取较大值，即风投机构具备较高资源整合能力时，整个风投市场更有可能达成高效的点E2(0，0，1)演化稳定均衡状态。

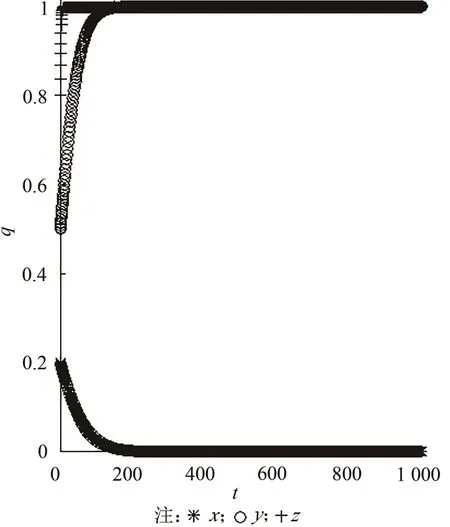
图1 θ赋值为0.1所对应三方演化稳定走势Fig.1 Tripartite evolutionary stability when θ equals to 0.1

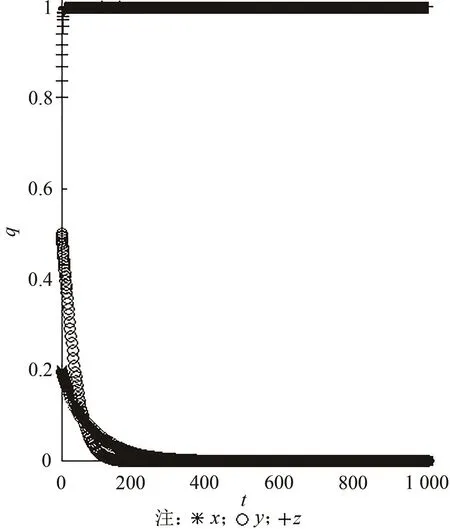
图2 θ赋值为0.2所对应三方演化稳定走势Fig.2 Tripartite evolutionary stability when θ equals to 0.2

5.3 现实证据

截至目前，尚未发现国外的中央政府或地方政府出台类似政策。就国内而言，自2014年北京市政府率先出台风投机构直接补贴政策以来，虽然有其他地方政府跟进，但由于政策落地时间太短，这些地方政府此后均未再对相关政策进行过调整。实际情况决定无法获得多个阶段博弈所对应的三方数据，也就无法开展较为规范的实证研究来验证政府直接补贴政策长期无效的结论。转换思路，因为缺乏政策粘性是政府直接补贴政策长期无效的内在机理，所以只要证明直接补贴政策缺乏政策粘性就可以间接证明相关结论。由于天使投资在概念界定上远比创业投资明确，下面针对北京市和天津市的天使投资状况进行分析。相关分析数据均引自新芽网(www.newseed.cn)。具体从以下两个角度进行分析。

5.3.1 平均增长率 如上所述，若政府直接补贴政策及后续调整具备政策粘性，则有助于新进入和已进入的风投机构在当地持续开展新投资业务。即，出台直接补贴政策城市的天使投资增长率应该要高于其他城市，或者即使出现系统性因素导致全国范围内天使投资出现衰退，其下降幅度也应相对较小。具体方法：首先计算出台直接补贴政策之后历年天使投资增长率，再求均值以消除随机扰动因素。因数据量太少，不能使用均值分析和方差分析等方法。

采用平均增长率法时必须要考虑到此方法不适合基数很小的城市，因为微小程度的变化可能就会引发增长率的巨大反应。天津市2014年仅有2起天使投资事件，2015年出台直接补贴政策后发生7起，虽然仅增加5起，但反映到增长率方面其增幅就高达250%。北京市2014年发生347起天使投资事件，2015年发生369起，虽然增加了22起，但反映到增长率方面其增幅仅为6.34%。因此，采用北京市数据计算出的平均增长率，其稳健性和可靠性要明显优于天津市。通过计算，北京市2014—2018年5年内天使投资平均增长率为-2.48%，而全国同期平均增长率则为25.97%。这足以说明北京市的直接补贴政策缺乏政策粘性。

5.3.2 个案调查法 个案调查法即针对已经在某地开展过投资活动并获得直接补贴的风投机构，通过调查其后续投资活动，以判断直接补贴政策是否激励风投机构持续在当地开展投资活动。2015—2018年天津市共发生天使投资事件23起，其中2起投资主体没有公开披露，其余21起由24家风投机构主导。然而，这24家风投机构中竟然没有任何一家在天津开展过第二次天使投资活动。由此可以判断，天津市2015年出台的《天使投资引导资金管理暂行办法》缺乏政策粘性。

以上分别采用平均增长率和个案调查法验证了北京市和天津市出台的直接补贴政策明显缺乏政策粘性，从而间接验证了政府直接补贴政策长期内无效的结论。

6 政策建议

根据上述结论已知政府针对风投机构的直接补贴政策在长期中无效，但结论4.2说明仍存在某些政策调整空间来刺激风投机构开展更多投资活动，并最终改善创业企业的融资环境。基本政策导向是在提升θ值的同时也要尽量降低k值，即提升风投机构资源整合能力的同时，努力降低金融市场平均利率水平。具体政策建议如下。

6.1 促进增值服务中介发展，完善创业生态系统

如前所述，资源整合能力是风投机构的政策应变、与创业团队沟通协调、企业管理、财务运营和市场营销等各种能力的综合体现。要想有效提升风投机构的资源整合能力，企业内部化方式并非唯一途径，且多数情况下难以操作。例如，在开展多个股权投资项目之后，即使不考虑行业跨度，风投机构本身的投资团队是否有足够时间和精力而事无巨细、事必躬亲地开展企业日常管理与市场开拓？如果通过市场招聘方式来完成相关业务，若后续出现投资项目规模收缩或进入新行业，暂时赋闲的专家是否应马上被辞退？但如果人员频繁流动，特别是核心骨干人员流失，一定会降低风投机构的资源整合能力。智库机构、猎头公司、市场策划公司、审计师事务所、律师事务所、会计师事务所等中介机构往往实时掌握并指导利用政府政策，是创业生态系统的重要组成部分。通过有序和规范的竞争，这些中介机构能够向风投机构提供高质量的价值增值服务，一旦双方形成长期友好的利益互动，必将大大提升风投机构的资源整合能力。地方政府应该高度重视、主动出击，通过税收优惠、创业园区物理空间配套等政策不断引进优质服务中介，促进相关创业服务中介行业的持续健康发展。

6.2 借鉴YOZMA模式，提高风投机构的准入门槛

资本雄厚、人才济济的风投机构往往具备优良的资源整合能力，而粗放式发展风投行业反而可能造成某地区局部金融风险的集聚。因此，地方政府应本着宁缺毋滥的态度，仅允许有较高资质的风投机构在本地开展投资活动。具体方式可借鉴以色列YOZMA计划：由地方政府出资建立母基金，再由母基金以不高于50%的份额投资多只民营风险投资基金；每一只基金必须由知名国外风险投资机构和国内金融机构组成，且仅能在本地开展与高科技产业相关的风险投资活动；同时，在母基金投资之初就约定好私人投资者以优惠价格买断政府在基金中权益的权利。类似政策的实施将会保证相关风投机构具备良好的资源整合能力，在保证风投机构获得优异投资回报和本地经济新动能不断增长的同时，也可以培养一批本地风险投资人才，从而为当地风投行业的健康和持续发展奠定基础。

6.3 引导资本脱虚向实，完善地区金融市场

作为资金使用价格，平均利率k一方面直接体现金融市场上资金供求的真实状况，另一方面也可以视为不同产业内资金使用价格的加权平均值。针对某些行业或重要商品的资本炒作与金融空转，势必会抬升整个金融市场的平均利率水平。对于地方政府而言，营造良好的营商环境，利用法律和经济手段抑制国内外游资的炒作之风，平滑重要商品价格波动的预期，都是降低平均利率水平的基本功课。此外，由于平均利率k也能大致反映某地区金融市场的完善程度，因此地方政府能够通过不断完善和发展地区内金融市场来降低整体平均利率水平。在间接融资渠道，成立专门智库积极总结各家商业银行落实支持实体经济的成功经验，及时解决所遇到的问题，引导资本脱虚向实，切实改善实体经济的融资环境；在直接融资渠道，应重新审视地区性股权交易中心在当地股权投资交易中的作用，转变经营机制与盈利模式，引导社会资本有效对接优质企业资源，缓解中小企业特别是创业企业的融资约束。