供应商风险规避下基于期权契约的政企联合储备应急物资模型

刘 阳，田 军，冯耕中，扈衷权

（西安交通大学 管理学院，陕西 西安 710049）

0 引言

我国是世界上遭受自然灾害最为严重的国家之一，灾害种类多，分布地域广，发生频率高。根据应急管理部公布的2017年全国自然灾害基本数据，洪涝、台风、干旱等灾害造成全国1.4亿人次受灾，979余人死亡失踪，直接经济损失3018.7亿元［1］。2018年9月发生的台风“山竹”，造成广东等地约300万人受灾，160.1万人被迫紧急转移，对社会稳定和经济发展造成了严重的影响［2］。为了快速响应与处置突发灾情，政府会在突发灾害发生前储备一定数量的应急物资，在突发灾害发生时可以迅速将此部分可用物资调拨至受灾区域。由于突发灾害具有突发性、随机性，且绝大多数应急物资均有保质期或使用期限，要求政府灾前预先储存无限规模的应急物资是不现实的，也是行不通的。相反，中央政府和各级地方政府应该充分利用、发挥市场机制的激励与约束作用，鼓励应急物资生产（储备）企业与政府建立合作关系，构建政府和企业共同参与的应急物资代储协议框架。为了更好地管理与协调政府和企业组成的供应链系统，近年来越来越多的学者利用供应链契约理论帮助政企制定合理的决策方案，以企满足突发条件下受灾人群对应急物资的巨大需求。

在众多供应链契约中，期权契约相比其他契约在柔性供应、渠道协调、规避风险以及节约成本等方面的优势明显［3，4］，因此在应急物流与应急管理领域得到了广泛的应用和认可。Liang等［5］设计了应急物资两步交付流程，引入期权契约建立应急物资二项式期权定价模型，得到了实现政府（买方）成本和企业（卖方）收益帕累托改善的柔性契约机制。田军等［6］考虑现货市场和突发事件发生时刻对政企应急物资储备策略的影响，利用实物期权契约构建了应急物资采购模型，研究表明该模型有利于政府控制成本与保障企业合理的利润。与田军等［6］不同，张海青等［7］认为企业可以以生产能力形式为政府代储应急物资，利用能力期权契约构建了应急物资采购模型，有利于政府节约成本，同时也合理补偿了企业紧急生产成本，使得企业有动机参与应急物资代储合作。通过梳理现有文献发现，目前绝大多数研究假设政企是风险中性的，并没有考虑决策者行为偏好因素对应急物资协议代储框架的影响。但在现实情况下，应急物资采购市场是一个明显的买方市场［8］，由于突发灾害引起的应急物资需求种类和数量具有极大的不确定性，供应商很可能面临着因持有过多应急物资而带来的风险损失，因此供应商通常选择较为保守的决策，即是风险规避的。但是不难发现，在对商业供应链的研究中考虑决策者行为偏好因素非常普遍，例如Agrawal和Seshadri［9］分析了零售商的风险规避特性对分发商和零售商的影响，研究表明零售商的风险规避特性有利于实现分发商收益的最大化，同时使得零售商降低货物持有数量而增加销售价格。Gan等［10］假设供应链系统包括供应商和具有风险规避特性的零售商，通过在风险共享契约中增加退货策略，实现了供应链系统协调。Wang和Webster［11］在单期报童模型中，利用Kinked型分段函数刻画经理的风险规避特性，研究表明：当缺货成本不可忽略时，风险规避特性促使经理订购更多的货物。叶飞与林强［12］假设风险规避型零售商与风险规避型供应商组成的供应链系统，研究零售商和供应商之间的Stackelberg博弈关系，提出了协调供应链的收益共享契约机制，并分析了零售商和供应商的风险规避特性对供应链收益的影响。王虹与周晶［13］分析了单渠道和多渠道情景下的供应链协调策略，给出了供应商在风险规避特性影响下选择直销渠道的条件。目前，在应急管理领域鲜有针对应急物资供应商风险规避特性的研究，更缺少关于供应商风险规避特性对政企达成契约合作的可能性、双方的决策策略与成本收益影响的研究。

Kahneman与Tversky［14］提出的前景理论在实践中体现较好的适用性［15～17］，因此本研究尝试运用前景理论刻画供应商风险规避特性，引入期权契约到政企组成的供应链系统，构建基于期权契约的政企联合储备应急物资模型，并对该模型进行扩展。本研究构建的政企联合储备应急物资模型更加贴近我国国情与应急物资储备的现实条件，既可以提高政府应急物资保障能力，有利于实现供应链协调与政企双赢，也为政府采购与储备应急物资提供了操作策略与指导法则，也是对应急物资储备与采购理论的有益补充。

1 问题描述与假设

1.1 决策过程

在风险规避型供应商与政府组成的供应链系统中，政企构建的期权契约关系包括两部分：常规采购与柔性采购，常规采购是指政府在突发灾害发生前预先采购并储存应急物资（Q），柔性采购是指供应商按照契约约定生产并代储应急物资（q）。政企双方的决策顺序与内容如下：灾前，政府以批发价格w从企业处采购Q单位的应急物资作为常规储备，并向企业提供一个采购协议（o，e），承诺为企业代储的单位柔性物资先行支付o。然后，供应商认真考虑是否接受政府提供的采购协议，如果接受则首先满足政府的常规采购部分，并确定应急物资柔性储备数量。在契约期内，如果突发灾害发生，政府根据应急物资的实际需求量（x）决定是否执行采购期权与具体的采购数量。

1.2 假设条件

为了使得本研究提出的期权契约机制下政企联合储备应急物资模型具有现实意义和应用价值，下面不失一般性地作出如下假设：

（1）假设政企签订期权契约的时长与应急物资保质期（使用期限）相同，此假设表明期权契约机制下政企联合储备应急物资模型是单周期的。

（2）假设突发条件下政府不得以强制性行政手段（如强制征用、调用等）从应急物资供应商处获取所需物资，此假设是要充分展现政企联合储备应急物资模型在市场机制下的效果。

（3）假设政府灾前采购的常规物资与应急条件下采购的柔性物资来源于同一个供应商，即单一供应商，说明政府与风险规避型供应商通过期权契约形成一对一的两级应急物资供应链系统。

（4）通常情况下，地震、洪涝等突发灾害从发生到产生巨大影响的时间小于政府应对灾害、实施救援救灾的时间，因此与刘阳等［18］研究假设一致，不考虑突发灾害持续时间对政府采购活动的影响。

（5）与文献［6～8，19］研究假设一致，政府批发应急物资的价格w为外生变量。

（6）与李刚等［20，21］研究假设一致，供应商风险规避特性与政府采购所需物资的执行价格存在正相关关系，即供应商风险规避特性越强，政府需要支付的单位物资期权执行价格越高。

（7）根据Wang与Liu［22］的研究结论，假设政府预先支付的期权价格与应急条件下采购所需物资的期权执行价格存在负相关关系，即政府支付的期权价格越高，购买所需物资的期权执行价格越低。

（8）采用分段线性价值效用函数描述供应商的风险规避特性，使用风险规避系数λ表示。供应商期望效用函数为E［U（Π（q））］＝Π（q）+（λ-1）L（q），Π（q）为期望收益，L（q）为期望利润损失。

1.3 符号说明与约束

X：应急物资需求量，假设X服从（0，Qm）上的随机分布，x为应对突发灾害所需的应急物资实际需求数量，概率密度函数为f（x），累计分布函数为F（x），F（x）与其反函数F-1（x）都是递增函数，且F（Qm）＝1，Qm为应急物资的最大需求量。

θ：突发灾害的发生概率，0＜θ≤1。

c：应急物资单位生产成本。

h：应急物资单位储存成本。

为了使得期权契约具有实际意义以及得到的模型分析结果不失一般性，现对期权契约相关参数进行如下约束：

（1）c+h＞o+v，防止供应商为政府储备无限量的柔性物资。

（2）e＞v，保证供应商有动机为政府代储柔性物资，而不是将所储物资按照残值处理。

（3）o+e＞w，保证供应商会按照契约约定为政府供应柔性物资，而不是将代储的应急物资在现货市场上售出。

（4）M＞o+e，保证政府会按照契约约定从企业处采购所需物资，而不是承担单位物资缺货成本。

2 无期权契约时的决策模型

2.1 供应链集中决策模型

供应链集中决策模型是政府与应急物资供应商作为一个整体，集中决策应急物资的储备数量（Qs），目标是实现整个供应链系统的成本最小化。供应链集中决策模型下的系统成本函数如（1）式所示：

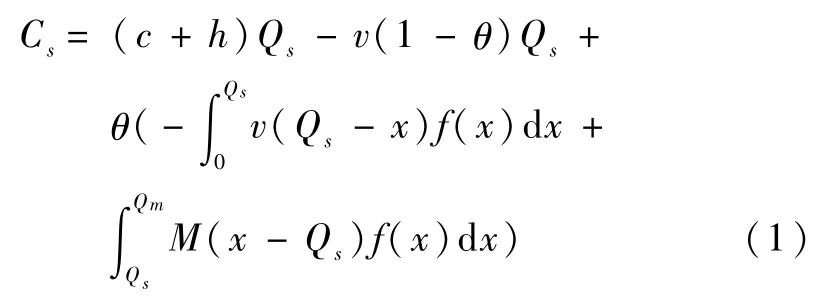
式中：第1项为应急物资的生产与储存成本，第2项为突发灾害未发生时应急物资的残值收益，第3项为应对突发灾害时由于应急物资实际需求数量的不同而产生的残值收益与缺货成本。

对（1）式求解关于Qs的一阶与二阶条件，得到：

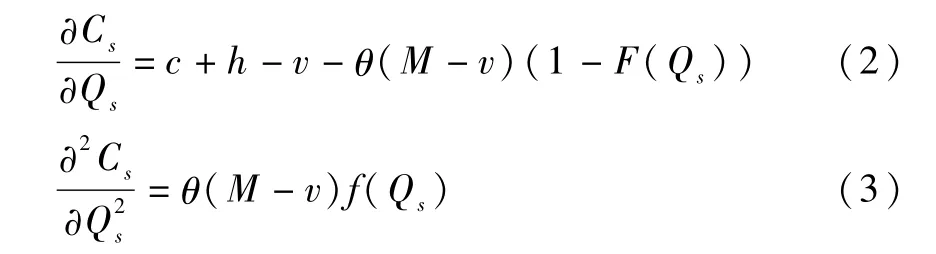
由于（3）式大于零，说明供应链集中决策模型下存在使得供应链系统成本取得最小值的应急物资最优储备量：

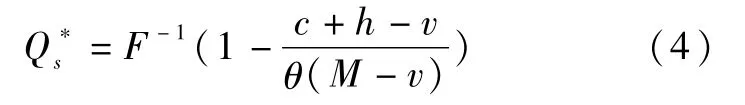
2.2 政府单独储备模型

政府单独储备模型属于政府管理库存，是指突发灾害发生前政府购买一定数量的应急物资并储存在应急储备库（Qd），但是受到资金条件、储备条件等因素的影响，应急物资储备水平被大大限制，使得政府很可能面临突发需求下因应急物资供应不足而导致的潜在风险与缺货成本。政府单独储备应急物资模型下政企没有建立契约合作关系，供应商只会按照政府已经明确的采购数量进行生产供应，相应的利润也完全来自政府常规采购，政府利用此部分物资应对可能发生的突发需求，政府成本函数如（5）式所示：

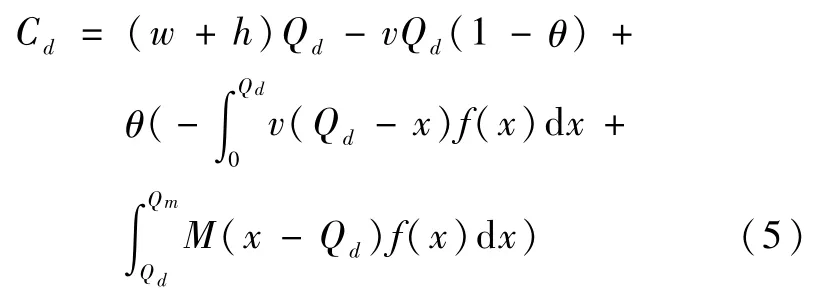
式中：第1项为应急物资的采购与储存成本，第2项为突发灾害未发生时应急物资的残值收益，第3项为应对突发灾害时由于应急物资实际需求数量的不同而产生的残值收益与缺货成本。

对（5）式求解关于Qd的一阶与二阶条件，得到：

由于（7）式大于零，说明政府单独储备模型下存在使得政府成本取得最小值的应急物资最优储备量：

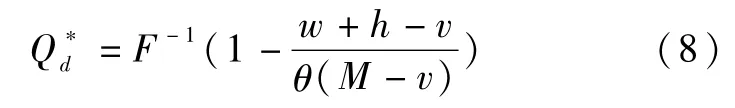
由于供应商期望利润损失为零，政府单独储备模型下的供应商期望效用为：

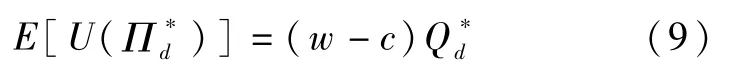
3 有期权契约时的决策模型

3.1 供应商期望利润

已知政府提供的期权契约与应急物资常规采购数量，供应商根据自身生产能力、成本参数等要素，以实现期望效用最大化为目标，决策应急物资的柔性储备数量q，产生的各类成本和收益如下：

（1）无论突发灾害是否发生，供应商获得的固定利润为（w-c）Q-（c+h-o）q。

（2）如果突发灾害发生，根据应急物资的实际需求数量，供应商期望利润包括以下三种情形：

1）当0＜x≤Q时，政府无需执行期权采购，供应商将此部分代储物资按照残值处理，获得的残值收益为vq；

2）当Q＜x≤Q+q时，政府需要执行部分期权，以期权执行价格从供应商处采购所需物资，供应商向政府供应订购的物资，并将剩余物资按照残值处理，获得的利润为e（x-Q）+v（Q+q-x）；

3）当Q+q＜x≤Qm时，政府需要执行全部期权，供应商获得的利润为eq。

（3）如果没有突发灾害发生，供应商利润为（1-θ）vq。

综上所述，风险规避型供应商的利润函数如（10）式所示

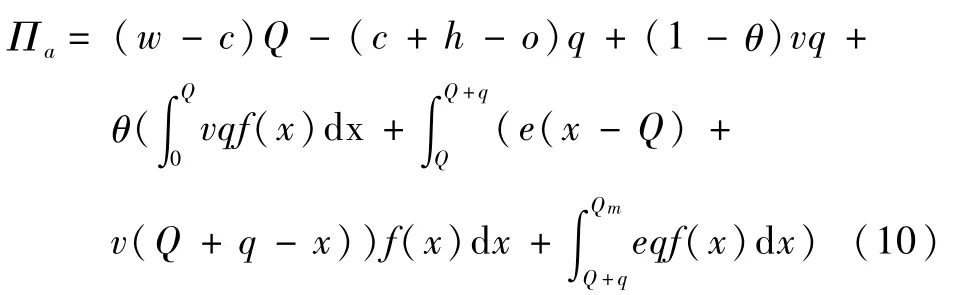
3.2 供应商期望利润损失

政府通过制定政企双方都能够接受的期权契约实现应急物资供应链协调，此时供应链系统成本最小。假设Q2＝（c+h-o-v）／（w+h-o-v），则有Q（w-c）-（c+h-o-v）q＝Q（w+ho-v）-下面以Q2为临界储备量，分为两种情况讨论供应商期望利润损失：

（1）当Q≥Q2时，则有Q（w-c）-（c+h-ov）q≥0，则供应商的期望利润损失为L（q）＝0。

（2）当Q＜Q2时，则有Q（w-c）-（c+h-ov）q＜0，则供应商的期望利润损失为：

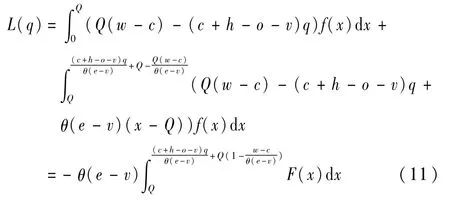
3.3 政企最优决策分析

在风险中性型政府和风险规避型供应商组成的应急物资供应链中，政企之间存在政府主导的、供应商从属的Stackelberg博弈关系。根据双方的决策顺序与内容，下面采用逆序推导法分析政企利益博弈模型。

3.3.1 供应商最优决策分析

当Q≥Q2时，供应商期望利润损失函数L（q）＝0，因此供应商期望效用函数为：

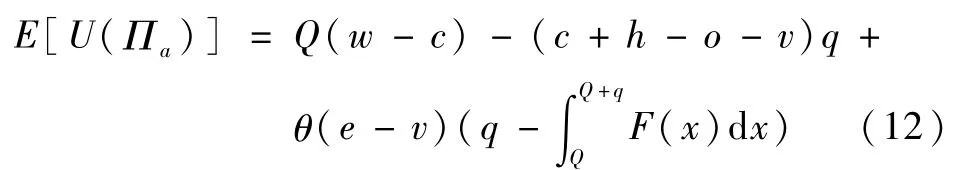
对（12）式求解关于q的一阶与二阶条件，得到：

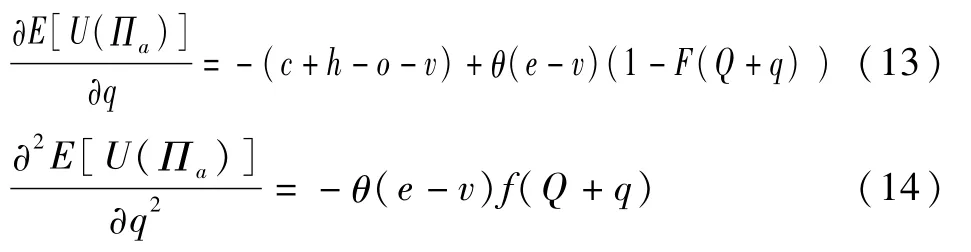
由于（14）式小于零，说明政府与风险规避型供应商联合储备模型下的供应商期望效用为q的凹函数，存在使得供应商期望效用取得最大值的应急物资最优储备量q*：

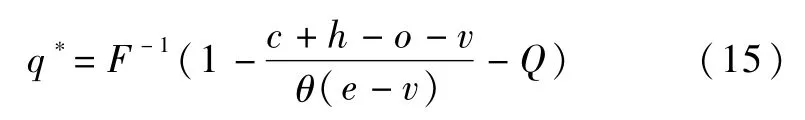
当Q＜Q2时，供应商期望利润损失函数为，因此供应商期望效用函数为：

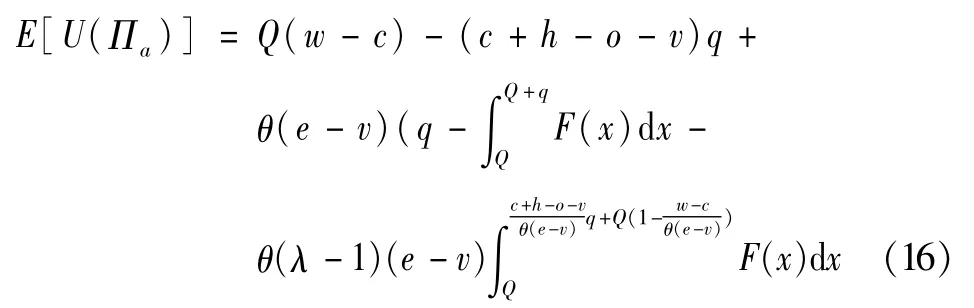
对（16）式求解关于q的一阶与二阶条件，得到：

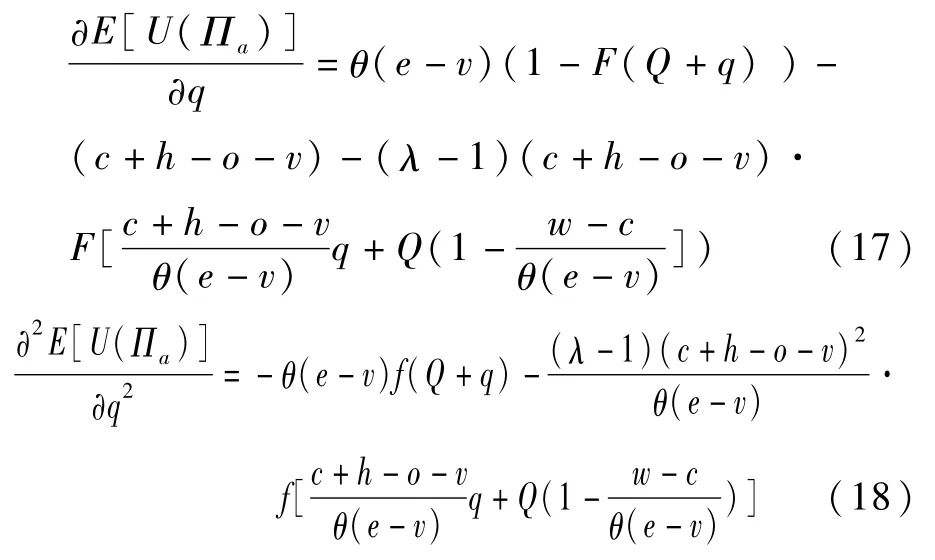
由于（18）式小于零，说明政府与供应商联合储备模型下的供应商期望效用为q的凹函数，存在使得供应商期望效用取得最大值的应急物资最优储备量q*，满足下式：

3.3.2 政府最优决策分析

政府根据供应商作出的决策策略，以激励供应商提高应急物资储备水平与控制成本为目的，决策常规应急物资的采购（储备）数量，政府成本函数如（20）式所示：

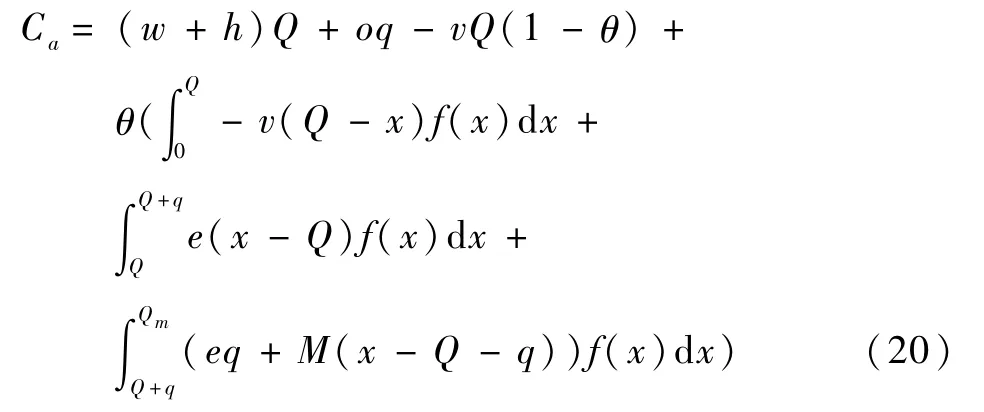
式中：第1项为应急物资的采购与储存成本，第2项为政府需要支付给供应商的期权费用，第3项为突发灾害未发生时应急物资的残值收益，第4项为应对突发灾害时由于应急物资实际需求数量的不同而产生的残值收益、采购成本与缺货成本。

当应急物资供应链达到协调时，满足Q+q*＝，变换（20）式可以得到：

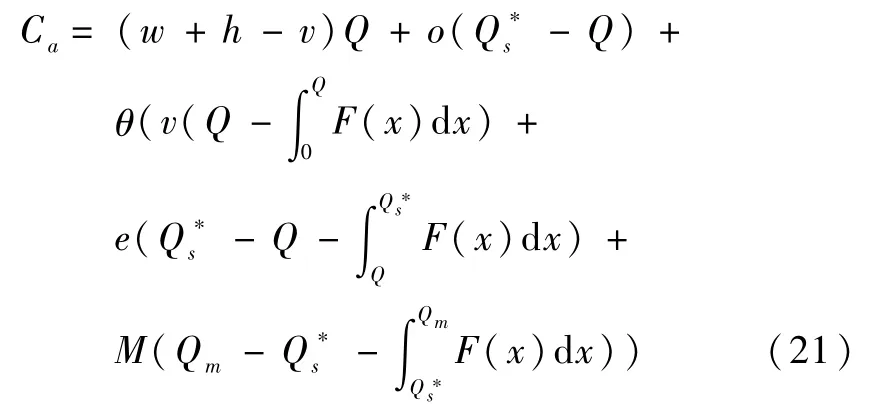
对（21）式求解关于Q的一阶与二阶条件，得到：

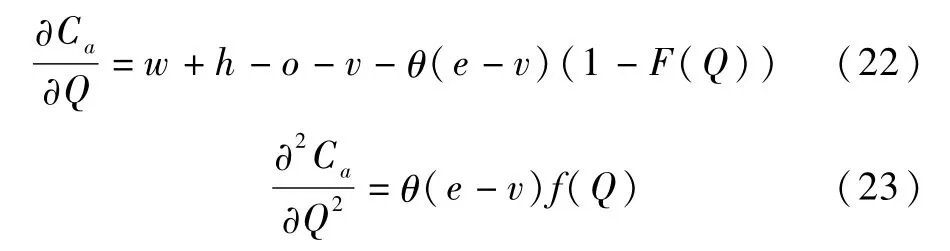
由于（23）式大于零，说明政府与供应商联合储备应急物资模型下，存在使政府成本取得最小值的应急物资最优储备量Q*：

在供应商风险规避情形下，分析供应商风险规避特性对政企应急物资最优储备量的影响，得到命题1。

命题1当Q*≥Q2时，政企应急物资最优储备量与供应商风险规避系数λ无关；当Q*＜Q2时，随着供应商风险规避系数λ的增加，政府最优储备量Q*增加，供应商最优储备量q*减少。

命题1说明，当Q*≥Q2时，政企最优储备量与供应商风险规避特性无关。当Q*＜Q2时，供应商风险规避特性越强，承担风险的能力越小，因此储备的应急物资越少。对政府来说，为了保障在突发灾害发生时有充足的应急物资可用以及实现供应链的协调，应该增加自身应急物资储备量。

在供应商风险规避情形下，分析期权契约参数（o，e）对政企应急物资最优储备量的影响，得到命题2。

命题2在供应商风险规避情形下，政府应急物资最优储备量Q*随着期权价格o的增加而减小，供应商应急物资最优储备量q*随着期权价格o的增加而增加。

命题2说明，政府预先支付给供应商的期权价格越大，在紧急条件下采购所需物资的价格越低，即能以较低的单位物资采购价格（o+e）获取所需物资，因此政府倾向储备较少的应急物资。期权价格越高，供应商获得的固定收益越多，因此供应商倾向储备更多的应急物资。

将政企应急物资最优储备决策方案代入各自的期望效用函数，分析供应商风险规避特性、期权契约参数（o，e）对政府成本与供应商期望效用的影响，得到命题3与4。

命题3当Q*≥Q2时，政府成本、供应商的期望效用与供应商风险规避系数λ无关；当Q*＜Q2时，政府成本、供应商的期望效用随着供应商风险规避系数λ的增加而增加。

命题3说明，当Q*≥Q2时，供应商风险规避特性不会影响政企成本收益。当Q*＜Q2时，供应商风险规避特性越强，政府储备物资越多，相应的投入成本越多。供应商风险规避特性越强，越害怕物资库存风险，因此会减少应急物资储备量，避免更多的收益损失，则供应商期望效用增加。

命题4在供应商风险规避情形下，政府成本与供应商期望效用随着期权价格o的增加而减小。

命题4说明，期权价格增加虽然增加了供应商应急物资储备量，但却大大降低了应急物资的单位购买价格，使得供应商期望效用减少。供应商储备物资的数量增加，使得政府减少了常规物资的采购与储存成本，因此政府成本是减少的。

3.4 期权契约机制与政府单独储备决策对比分析

期权契约为政府和供应商构建应急物资储备合作协议提供了可能性，与政府单独储备模式相比，期权契约机制下政企联合储备模式既要保证供应商有动机为政府代储应急物资，又不能增加政府成本，因此需要满足的不等式如（25）式所示：

当Q*＜Q2时，得到：

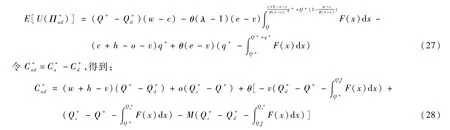
由于（26）式、（27）式与（28）式极其复杂，无法直接得出o和e的确切关系，因此下面利用一个数值算例，求解保证政府成本与供应商期望效用都得到改善的条件。假设θ＝0.2、c＝40、ω＝50、v＝20、h＝0.1、M＝300、U＝20000、λ＝1.05，应急物资需求量X服从（0，U）的均匀分布，计算得出：（1）当Q*≥Q2时，期权价格 o的取值范围为（0，7.38）；当Q*＜Q2时，期权价格o的取值范围为（8.40，10.44），由此表明实现供应链协调与政企双赢的条件为o∈（0，7.38）∪（8.40，10.44）。

4 模型扩展

为了使得政企联合储备应急物资模型具有现实价值与广泛的应用范围，本节在供应商风险规避的基础上，进一步探讨现货市场、政府强制性要求对政企应急物资储备决策策略以及双方成本收益的影响。

4.1 现货市场和供应商风险规避特性对政企决策的影响

假设存在一个现货市场，应急物资现货价格为η，突发需求发生时政府可以从供应商与现货市场两种渠道采购所需物资，按照2.1与2.2节的思路，得到供应链集中决策模型下应急物资最优储备量与政府单独储备模型下的应急物资最优储备量以及政府成本与供应商期望效用。下面将对存在现货市场和供应商风险规避情形下的政企联合储备应急物资模型进行分析，并与供应链集中决策模型和政府单独储备模型的结果进行比较。

政企双方的决策顺序与内容是：灾前，政府以批发价格w从供应商处采购Q单位的应急物资作为常规储备，并向企业提供一个采购协议（o，e），承诺为企业代储的单位柔性物资先行支付o。然后，供应商认真考虑是否接受该采购协议，如果接受则首先满足政府的常规采购部分，同时决策需要代储的应急物资柔性数量。在契约期内，如果突发灾害发生，政府根据应急物资的实际需求量（x）和现货市场价格η决定是否执行期权与采购数量。假设应急物资批发价格低于现货市场价格（w＜η），这与实际情况是一致的。政府和供应商对未来的现货市场价格具有相同的预期判断，假设应急物资现货价格低于应急条件下期权执行价格的概率为φ，φ＝P｛η＜e｝。

4.1.1 供应商期望利润与期望利润损失

存在现货市场和供应商风险规避情形下，供应商利润函数如（29）式所示：

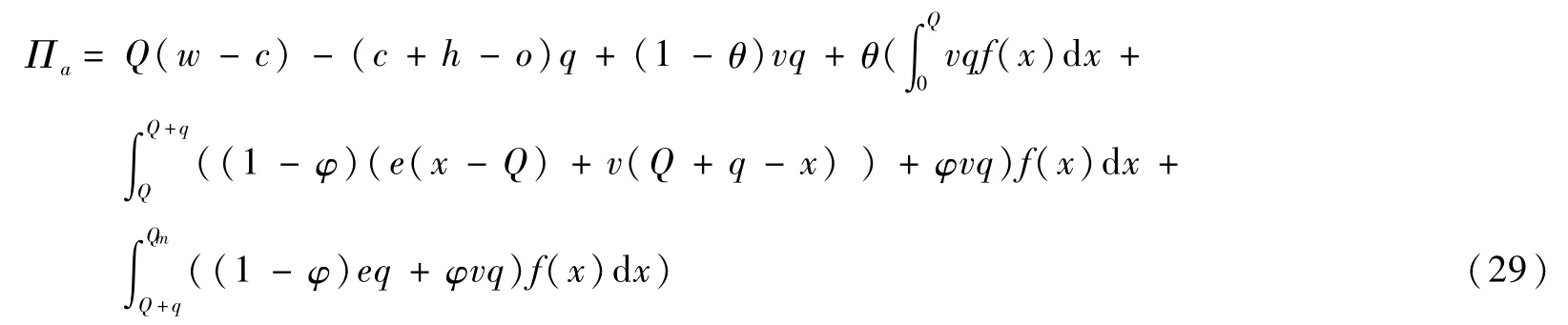
式中：前2项为供应商固定收益，第3项为突发需求未产生时应急物资的残值收益，第4项为现货市场条件下应对突发需求时因应急物资实际需求数量不同而产生多种收益。

4.1.2 政府与供应商最优决策分析

当Q≥Q2时，供应商期望效用函数为：

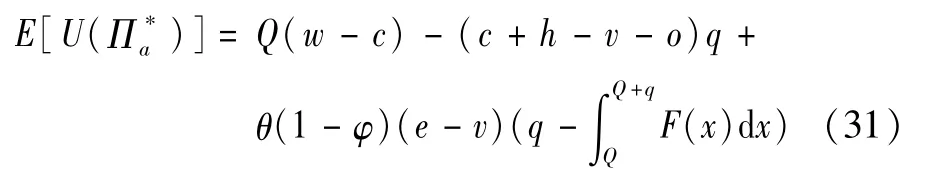
求解得出使得供应商期望效用取得最大值的应急物资最优储备量q*：

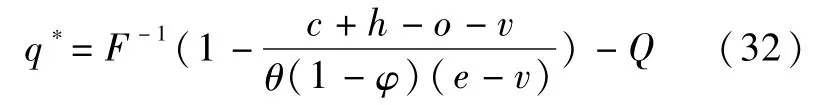
当Q＜Q2时，供应商期望效用函数为：

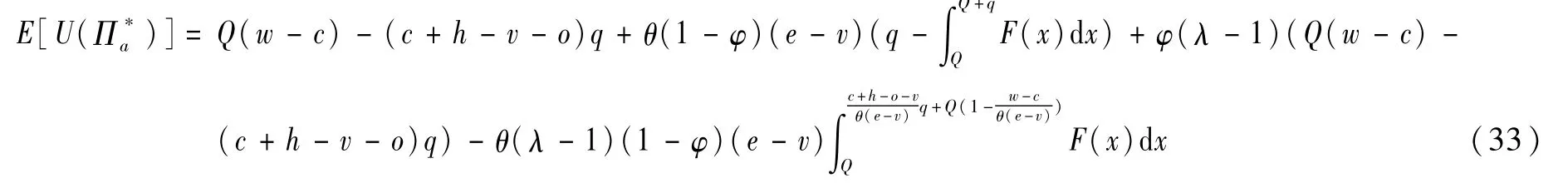
求解得出使得供应商期望效用取得最大值的应急物资最优储备量q*，满足下式：

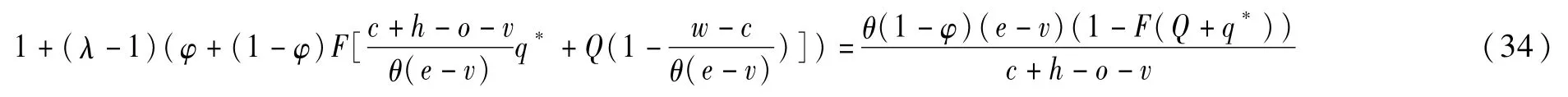
存在现货市场和供应商具有风险规避特性情形下，政府成本函数如（35）式所示：

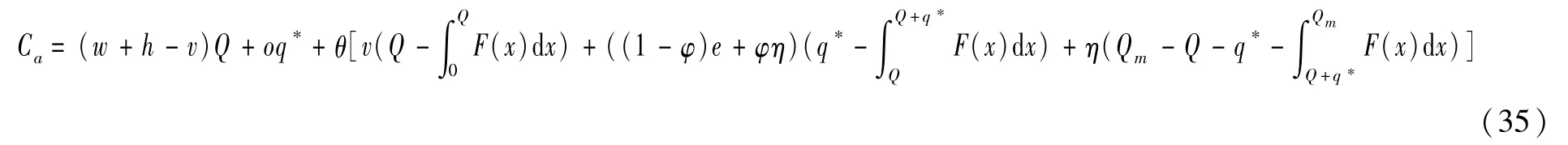
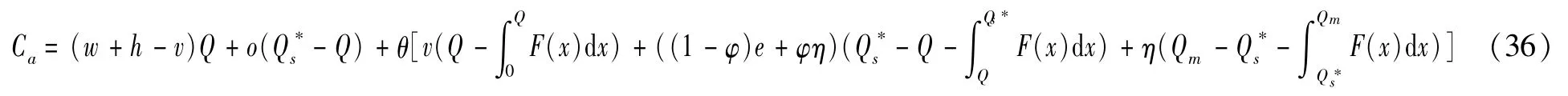
求解得出使得政府成本取得最小值的应急物资最优储备量Q*：

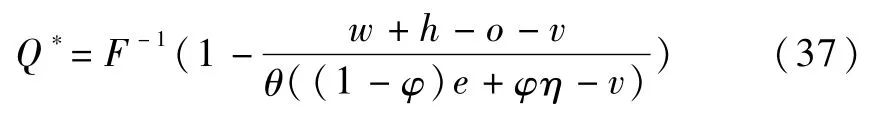
存在现货市场和供应商风险规避情形下，分析供应商风险规避特性对政企应急物资最优储备量、政府成本与供应商期望效用的影响，得到命题5与6。

命题5 存在现货市场和供应商风险规避情形下，当Q*≥Q2时，政企应急物资最优储备量与供应商风险规避系数λ无关；当Q*＜Q2时，随着供应商风险规避系数λ的增加，政府最优储备量Q*增加，供应商最优储备量q*减小。

命题5说明，存在现货市场和供应商风险规避情形下，当Q*≥Q2时，供应商的期望利润损失为零，即不会对其期望效用产生影响，因此供应商风险规避系数不会对政企应急物资最优储备量产生影响。当Q*＜Q2时，供应商风险规避特性越强，承担风险的能力越小，因此储备应急物资的数量越少。对政府而言，为了保障在突发需求产生时有可供调配的应急物资以及协调供应链系统，应该提高自身应急物资的储备水平。

命题6存在现货市场和供应商风险规避情形下，当Q*≥Q2时，政府成本、供应商期望效用与供应商风险规避系数λ无关；当Q*＜Q2时，随着供应商风险规避系数λ的增加，政府成本与供应商期望效用增加。

命题6说明，存在现货市场和供应商风险规避情形下，当Q*≥Q2时，政府成本、供应商期望效用和供应商风险规避特性不存在相关性。当Q*＜Q2时，供应商风险规避特性开始发挥作用，随着λ的增加，供应商对风险厌恶程度越高，因此政府倾向储备更多的应急物资，使得常规采购与储存成本增加，进而导致政府成本增加。供应商风险规避特性越强，越害怕物资库存风险，储备的应急物资越少，因此期望效用是增加的。

存在现货市场和供应商风险规避情形下，分析应急物资现货价格对政府最优储备量与成本的影响，得到命题7。

命题7存在现货市场和供应商风险规避情形下，政府最优储备量Q*与成本随着现货市场价格η的增加而增加。

命题7说明，应急物资现货市场价格越高，政府从现货市场上采购所需物资的难度越大，增加了政府成本。为了避免突发灾害发生时高价采购所需物资，政府需要提高自身应急物资的储备水平。

存在现货市场和供应商风险规避情形下，分析期权契约（o，e）对政企应急物资最优储备量、政府成本与企业期望效用的影响，得到命题8。

命题8存在现货市场和供应商风险规避情形下，随着期权价格的增加，政府最优储备量Q*减小，供应商最优储备量q*增加，政府成本与供应商期望效用减小。

命题8说明，期权价格增加虽然增加了供应商为政府代储的柔性物资数量，但却大大降低了单位物资的购买价格，使得供应商期望效用减少。同时，为了协调供应链，政府会减少应急物资储备量，使得采购与储存成本减少，因此政府成本是减少的。

4.1.3 期权价格的取值范围

与政府单独储备模型相比，存在现货市场和供应商风险规避情形下的政企联合储备应急物资模型也需要保证政府成本与供应商的期望效用都得到有效改善。本节利用4.4节所述的数值算例，假设应急物资现货市场价格η＝200，现货市场价格低于期权执行价格的概率φ＝0.1，其他参数保持不变，计算得出：当Q*＜Q2时，期权价格o的取值范围为（9.92，11.55），说明实现供应链协调与政企双赢的条件为o∈（9.92，11.55）。

4.2 政府强制性要求和供应商风险规避特性对政企决策的影响

本文假设政府对供应商储备应急物资的数量没有强制性的要求，也就是说供应商最优储备量是政企博弈的结果。但在实际情况下，应急物资供应链是非盈利性的，政府可能会强制要求供应商必须储备一定量的应急物资（q0）。当然q0也不宜太大，需要满足q0+Q＜Qm，供应商根据契约约定决策合适的应急物资储备数量（q1）。假设政府强制性系数为ρ，政府强制性要求情形下供应商应急物资储备总量为ρq0+（1-ρ）q1。按照2.1与2.2节的思路，得到下面将分析政府强制性要求和供应商的风险规避特性对政企联合储备应急物资模型的影响，并与供应链集中决策模型和政府单独储备模型的结果进行比较。

4.2.1 供应商期望利润与利润损失分析

政府强制性要求和供应商风险规避情形下，供应商利润函数如（38）式所示：

式中：前2项为供应商固定收益，第3项为突发灾害未发生时应急物资的残值收益，第4项为政府强制性要求下由于应急物资实际需求数量不同而产生的多种收益。

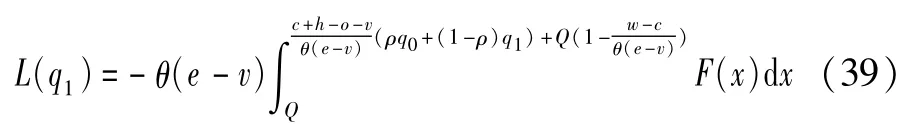
4.2.2 政企最优决策策略分析

当Q≥Q2时，供应商期望效用函数为：

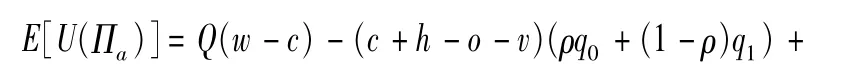
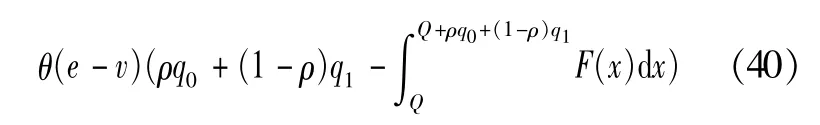
求解得出使得供应商期望效用取得最大值的应急物资最优储备量：

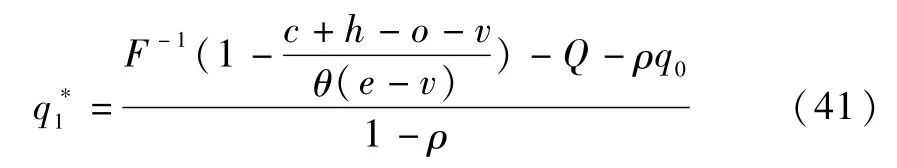
当Q＜Q2时，供应商期望效用函数为：

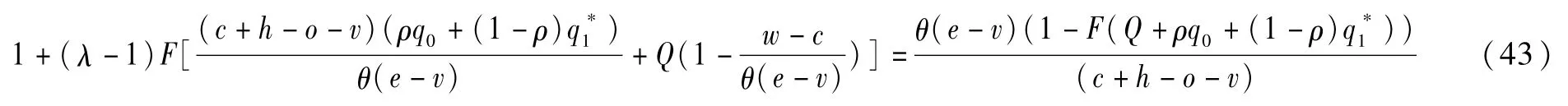
政府强制性要求和供应商风险规避情形下，政府成本函数如（44）式所示：

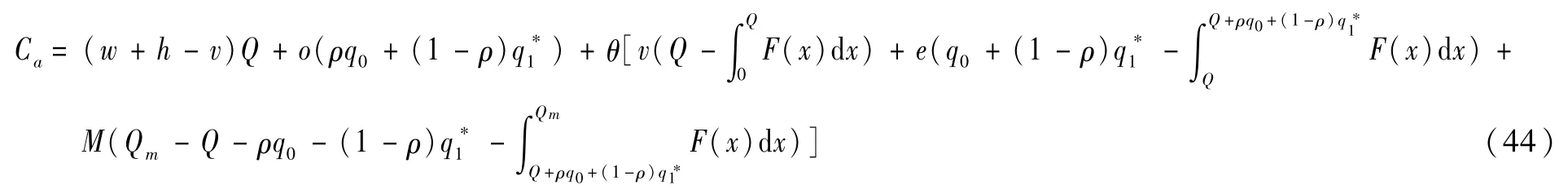
式中：第1项为应急物资的采购与储存成本，第2项为政府需要承担的期权费用，第3项为突发灾害未发生时应急物资的残值收益，第4项为政府强制性要求下应对突发灾害时因应急物资实际需求数量不同而产生的残值收益、采购成本与缺货成本。

当供应链达到协调时，满足Q+ρq0+（1-ρ），变换（44）式可以得到：

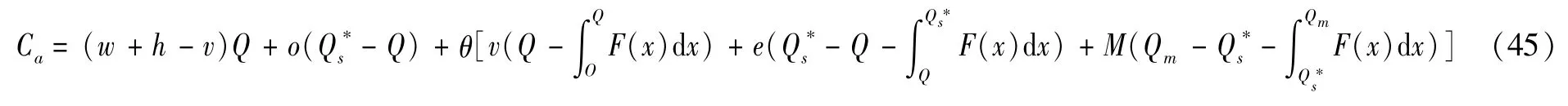
求解得出使得政府成本取得最小值的最优储备量Q*：

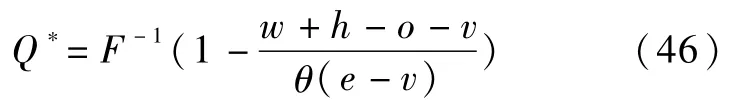
政府强制性要求和供应商风险规避情形下，分析供应商风险规避特性对政企应急物资最优储备量的影响，得到命题9。

命题9政府强制性要求和供应商风险规避情形下，当Q*≥Q2时，政企应急物资最优储备量与供应商风险规避系数λ无关；当Q*＜Q2时，随着供应商风险规避系数λ的增加，政府最优储备量Q*增加，供应商最优储备量减小。

命题9说明，政府强制性要求和供应商风险规避情形下，当Q*≥Q2时，供应商风险规避特性不会对政企应急物资储备决策方案产生影响。当Q*＜Q2时，供应商风险承担能力越小，应急物资储备数量越少。由此可见，为了保障突发条件下应急物资的可用性与实现供应链协调，政府应该增加自身应急物资储备水平。

政府强制性要求和供应商风险规避情形下，分析政府强制性系数对政企应急物资最优储备量的影响，得到命题10。

命题10政府强制性要求和供应商风险规避情形下，当Q*＜Q2时，供应商最优储备量随着政府强制性系数ρ的增加而增加；当Q*≥Q2时，，供应商最优储备量随着政府强制性系数ρ的增加而增加；（2）＜q0，供应商最优储备量随着政府强制性系数ρ的增加而减小。

命题10说明，政府强制性要求和供应商风险规避情形下，当Q*＜Q2时，供应商最优储备量与政府强制性系数ρ正相关。当Q*≥Q2时，如果＞q0，供应商最优储备量与政府强制性系数ρ正相关；反之，供应商最优储备量与政府强制性系数ρ负相关。

4.2.3 期权价格范围分析

与政府单独储备模型相比，政府强制性要求和供应商风险规避情形下的政企联合储备应急物资模型也需要保证政府成本与供应商的期望效用都得到有效改善。下面利用上述算例验证该模型的有效性，假设政府要求供应商必须储备的应急物资数量q0＝5000，政府强制性系数ρ＝0.3，得出：当Q*≥Q2时，期权价格o的取值范围为（0，7.38）；当Q*＜Q2时，期权价格o的取值范围为（8.40，10.44）。由此表明，实现供应链协调与政企双赢的条件为o∈（0，7.38）∪（8.40，10.44）。

5 结论

本文构建了供应商风险规避情形下基于期权契约的政企联合储备应急物资模型，分析了供应商的风险规避特性对政企应急物资最优决策方案以及双方成本收益的影响，探讨了现货市场、政府强制性要求对政企联合储备模型的影响，并结合数值算例得出了实现供应链协调与政企双赢的期权价格范围。本文提出了以下重要的管理启示：（1）政府应该适当提高期权价格，激励供应商储备更多的应急物资，在突发灾害发生时能以较低的价格采购所需物资，有利于控制政府成本与保障供应商的合理收益；（2）政府应该积极提高供应商承担风险的能力，提升供应商代储应急物资的积极性，降低政府储备应急物资的风险和库存水平；（3）政府应该积极拓宽应急物资的采购渠道，与供应商建立长久合作的关系；（4）政府强制性要求供应商储备一定量的应急物资是十分有必要的，在灾情初期可以为救灾救援提供更多的应急物资。本研究构建的政企联合储备应急物资模型为灾前储备物资和灾后采购物资提供了有效的指导意见，具有重要的现实价值。

但是本文只考虑了政府和风险规避型供应商组成的一对一的两级供应链系统，后续研究可以考虑更加复杂的供应链结构，如考虑政府和多个供应商组成的两级或三级供应链系统。另外，本研究假设供应链成员掌握的信息是对称的，后续研究可以考虑信息不对称下的政企联合储备模型。