THE EXISTENCE OF A NONTRIVIAL WEAK SOLUTION TO A DOUBLE CRITICAL PROBLEM INVOLVING A FRACTOL LOL
Gongbao LI(李工宝)† Tao YANG (杨涛)
Hubei Key Laboratory of Mathematical Sciences and School of Mathematics and Statistics, Central China Normal University, Wuhan 430079, China E-mail : ligb@mail.ccnu.edu.cn; yangt@mails.ccnu.edu.cn
1 Introduction
In this paper,we consider the existence of nontrivial weak solutions to a double critical problem involving a fractional Laplacian with a Hardy term:






The rest of the paper is organized as follows:in Section 2,we give some preliminaries.In Section 3,we introduce the weighted Morrey space and establish improved Sobolev inequalities,i.e.,we prove Proposition 1.3 and Corollary 1.4.In Section 4,we solve the minimization problems(1.12)–(1.13).In Section 5,we prove Theorem 1.1.
NotationWe use→and⇀to denote the strong and weak convergence in the corresponding spaces respectively.Write“Palais-Smale”as(PS)for short.N={1,2,···}is the set of natural numbers.R and C denote the sets of real and complex numbers respectively.By saying that a function is“measurable”,we always mean that the function is“Lebesgue”measurable.“∧”denotes the Fourier transform and“∨”denotes the inverse Fourier transform.Generic fixed and numerical constants will be denoted byC(with subscript in some case),and they will be allowed to vary within a single line or formula.
2 Preliminaries
In this section,we give some preliminary results.
Lemma 2.1(fractional Hardy inequality:Formula(2.1)in[26])Lets∈(0,1)andn>2s.Then we have



3 Proof of Proposition 1.3 and Corollary 1.4
In this section,we give some basic properties of a weighted Morrey space and then prove Proposition 1.3 and Corollary 1.4.
The Morrey spaces were introduced by Morrey in 1938[30]to investigate the local behavior of solutions to some partial differential equations.Nowadays the Morrey spaces are extended to more general cases(see[1,31,32]).Lettingp∈[1,+∞)andγ∈(0,n),the usual homogeneous Morrey space
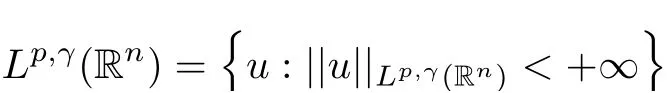



4 Solving the Minimization Problems(1.12)–(1.13)



Thus we have that˜v 6≡0.The rest is the sameas the proof of Proposition 4.1-(1),so Proposition 4.1-(2)holds.
(3)The proof is similar to Proposition 4.1-(1).Although Proposition 4.1-(3)has been proved in[2],the strategy we adopted in Proposition 4.1-(1)is more direct and effective.
(4) Imitate the proof of Proposition 4.1-(2). ?
Remark4.3To prove Proposition 4.1-(2),firstly we choose aminimizing sequence{uk}of Sµ(n,s,γ,0),then we prove that vk=|uk|∗is also aminimizing sequence of Sµ(n,s,γ,0),since 0≤γ<γH.Since vkis radial symmetric and decreasing,we can easily eliminate vanishing.If α>0 and 0≤γ<γH,the same strategy can be applied to the proof of Proposition 4.1-(1).W hen it comes to α>0 and γ<0,we fail to prove that vk=|uk|∗is a minimizing sequence of Sµ(n,s,γ,α),but(1.9)and(1.10)are very effective in this situation.
5 Proof of Theorem 1.1
We shall now use the minimizers of Sµ(n,s,γ,α)and Λ(n,s,γ,β)obtained in Proposition 4.1 to prove the existence of a nontrivial weak solution for equation(1.1).Recall that the energy functional associated to(1.1)is
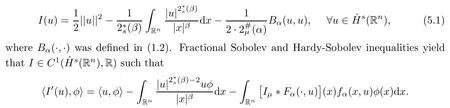
Note that a nontrivial critical point of I is a nontrivial weak solution to equation(1.1).
Lemma5.1(Mountain Pass Lemma,[37])Let(E,||·||)be a Banach space and let I∈C1(E,R)such that the following conditions are satisfied:
(1)I(0)=0;
(2)There exist ρ,r>0 such that I(u)≥ρ for all u∈E with||u||=r;





Hencevis a nontrivial weak solution of(1.1).
(II)If is the case thats∈(0,1),0≤α,β<2s Case(i)α=0<β<2sorβ=0<α<2s. In this case,the embeddings(1.9)and inequality(1.10)are still effective.Sinceα>0 orβ>0,we get a nontrivial weak solution to(1.1),as above,by using(1.9),(1.10)and Proposition 5.3. Case(ii)α=0 andβ=0. In this case,(1.9)and(1.10)are useless.Since the limit equation for(1.1)is by using the Nehari manifold method in[5],we can also get a non-trivial weak solution to(1.1),if 0≤γ<γH. Remark 5.4The method we adopt to prove Theorem 1.1 can be applied to prove a similar existence result for thep-Laplace type problem involving double critical exponents.To go further,we consider We say thatu∈D1,p(Rn)is a weak solution to(5.12)if for anyφ∈D1,p(Rn).The following main result holds: Theorem 5.5The problem(5.12)possesses at least a nontrivial weak solution provided that either (I)n≥2,p∈(1,n),0<α1,α2 (II)n≥2,p∈(1,n),0≤α1,α2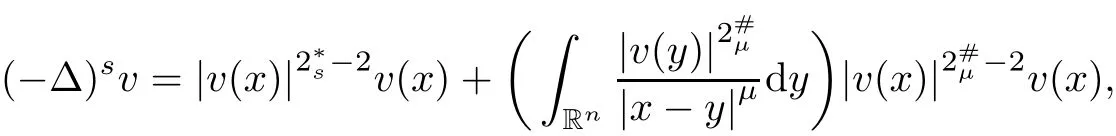
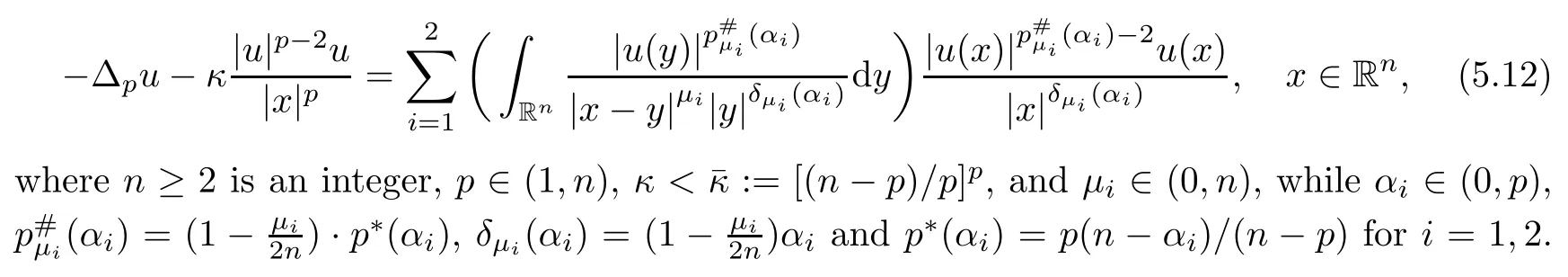
 Acta Mathematica Scientia(English Series)2020年6期
Acta Mathematica Scientia(English Series)2020年6期
