GENERALIZED ROPER-SUFFRIDGE OPERATOR FOR ε STARLIKE AND BOUNDARY STARLIKE MAPPINGS∗

Jie WANG (王洁) Jianfei WANG (王建飞)†

School of Mathematical Sciences, Huaqiao University, Quanzhou 362021, China

E-mail : wangjie5306@163.com; jfwang@hqu.edu.cn

where(z1,···,zn)∈Bnand the branch of the square root is chosen such that

The above Roper-Suffridge extension operator(1.1)has some remarkable properties:

(i)Iffis a normalized convex function onU,thenΦ[f]is a normalized convex mapping onBn;

(ii)Iffis a normalized starlike function onU,thenΦ[f]is a normalized starlike mapping onBn;

(iii)Iffis a normalized Bloch function onU,thenΦ[f]is a normalized Bloch mapping onBn.

Roper and Suffridge proved Property(i).Graham and Kohr[11]provided a simplified proof of Property(i)and also proved Property(ii).Later,Gong and Liu in[6]and[7]generalized the Roper-Suffridge extension operator from the unit ballBnto some Reinhardt domains in Cn.In the last 20 years,many work have been devoted to proving that the Roper-Suffridge extension operator preserves some subclasses of starlike mappings on Reinhardt domains in Cn;see e.g.[4,5,10,15,19,20,24,25].By using the Roper-Suffridge extension operator,a lot of normalized biholomorphic mappings with some special geometric or analytic properties can be easily constructed,which is an important reason why people are interested in the Roper-Suffridge extension operator.

Interestingly,a creative idea was developed by Elin[2],Elin and Levenshtein[3]and Graham et al.[12]for different generalizations and modifications of this operator in terms of some complex Banach spaces.They introduced a general construction which includes many known extension operators considered earlier,namely,the following operator

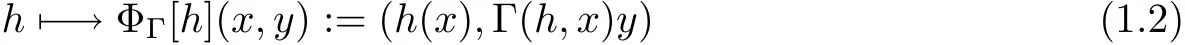
defined on the unit ball of the direct productX×Yof two complex Banach spaces,where Γ(h,x)is an operator-valued mapping obeying some natural conditions.Elin[2]proved that the above operator preserves starlikeness and spirallikeness under some conditions.Furthermore,Elin proposed the open problem[2,Open Problem(b)]:

Which condition doesΓpossess in order that the extension operator(1.2)preserves convexity?

One purpose of this article is to consider the above problem and give a natural condition such thatΦΓ[h]preserves convexity whenandhis convex on the unit diskU.This is achieved only relying on the conformal invariant property on the hyperbolic metric between two simply connected proper domains of C.The other purpose is to prove that the Roper-Suffridge extension operator preserves biholomoprhic starlike with respect to a boundary point of the unit ballBn.

This paper is organized as follows:in Section 2,we prove that the Roper-Suffridge extension operator preservesεstarlikeness on the open unit ball of C×X.Furthermore,we give convex constructions of much higher dimensions starting from convex mappings of the polydiskUn.Section 3 is devoted to discussing boundary starlike mappings on the unit ballBn.By introducing a subclass of boundary starlike mappings onBn,we prove that the Roper-Suffridge extension operator preserves almost boundary starlikeness of orderα.Furthermore,we propose some problems.

2 Roper-Suffridge Extension Operator and ε Starlikeness

2.1 ε starlikeness and hyperbolic metric

Definition 2.1Suppose thatXis a complex Banach space and thatΩis a domain inX.The domainΩcontaining the origin is said thatε-starlike if there exists a positive numberε,0≤ε≤1,such that for anyz,w∈Ω,one has(1−t)z+εtw∈Ωfor all 0≤t≤1.

In particular,whenε=0 andε=1,theε-starlike domain reduces to starlike domain with respect to the origin and convex domain,respectively.

Definition 2.2([6])Suppose thatXis a complex Banach space and thatΩis a domain inX.Letf:Ω→Xbe a locally biholomorphic mapping and 0∈f(Ω).fis called anεstarlike mapping onΩiff(Ω)is anε-starlike domain inX.

Whenε=0 andε=1,freduces to a starlike mapping and a convex mapping,respectively.

Definition 2.3([1])LetD⊂C be a simply connected proper open set.Suppose thatfis a conformal(biholomorphic)mapping of the unit diskUontoD.The hyperbolic metricofDis defined by the pull back(f−1)∗ds2,where

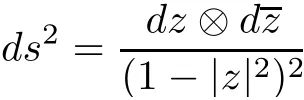
is the Poincar´e metric on the unit disk ofU.

It is straightforward to calculate that

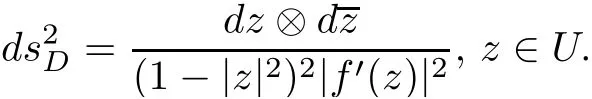
LetλDrepresent the density of the hyperbolic metric onD.Then we have

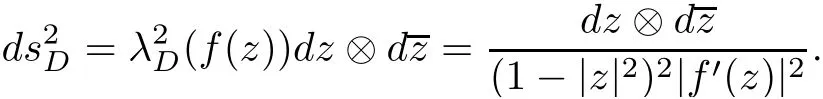
Hence,

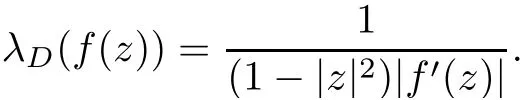
2.2 Two lemmas

To work out our main results,we need the next two lemmas which are associated with the hyperbolic metric.Lemma 2.4 can be found in Beardon and Minda[1].Lemma 2.5 is due to Wang and Liu in[26]

Lemma 2.4([1])Suppose thatΩis a proper simply connected domain of C.Letf:U→Ωbe holomorphic.Then

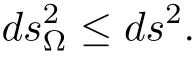
In particular,iffis biholomorphic,then

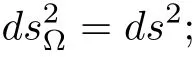
that is,

Lemma 2.5([26])Suppose thatΩ⊂C contains the origin.LetΩbe anε-starlike domain withΩ≠C.Then

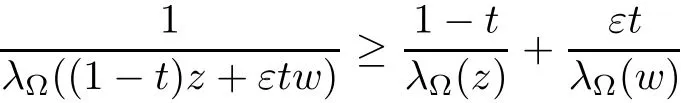
holds for allz,w∈Ωand 0≤t≤1.

2.3 ε starlikeness and Roper-Suffridge extension operator

2.4 Extension operator for higher dimensions

By using the Roper-Suffridge extension operator,Theorem 2.6 tells us how to construct biholomorphic convex and starlike mappings on the open unit ball B of the Banach space C×Xwhich starts from biholomorphic convex and starlike functionshof one complex variable on the unit diskUin C.Now we shall generalize the Roper-Suffridge extension operator from one complex variable to several complex variables due to the decomposition result of Suffridge[23].

DenoteUnby the unit polydisk in Cn,i.e.,Un={(z1,···,zn)∈Cn:|zj|<1,j=1,···,n}.Letf:Un→Cnbe a holomorphic mapping,written by

Thus,

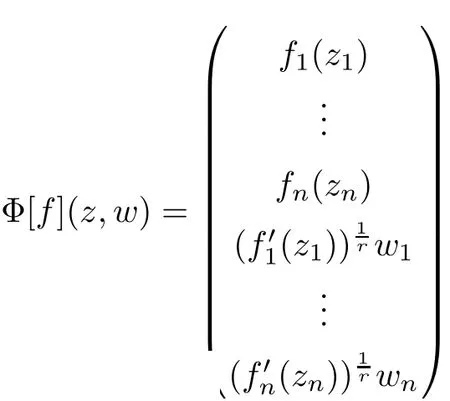
is a convex mapping on Bn,which completes the proof.

3 Roper-Suffridge Extension Operator and Boundary Starlikeness

3.1 Boundary starlike mappings

Suppose thatΩ⊂Cnand 0∈∂Ω.If the segment(0,z]is included inΩfor all givenz∈Ω,thenΩis said to be starlike with respect to the boundary pointw=0.The investigation of univalent starlike functions with respect to a boundary point was initiated in 1981 with the paper by Robertson of[22]in one complex variable.Later,several authors devoted their work to the study of boundary starlike functions;see[13,16].However,for higher dimensions,there is little work on the study of boundary starlike mappings.To our knowledge,the work of Liczberski and Starkov[14]is the most instructive on the subject.The object of this section is to introduce a new class of almost boundary starlike mappings of orderαon the unit ballBn.Then we prove that the Roper-Suffridge extension operator preserves boundary starlikeness on the unit ballBn.

3.2 Roper-Suffridge operator and almost boundary starlikeness of orderα

In this paper,we introduce a new subclass of S∂(Bn)as follows:

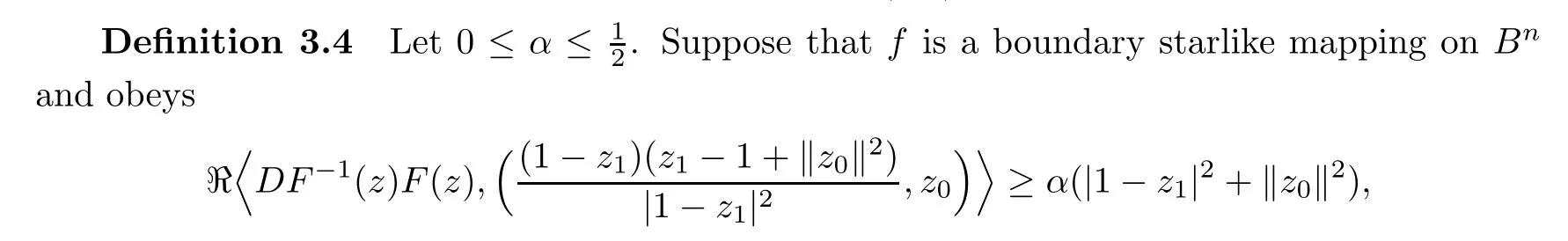
wherez∈Bn,z0=(z2,···,zn)∈Cn−1.ThenFis called an almost boundary starlike mapping of orderαonBn.

Naturally,we will ask the following question:

Does the Roper-Suffridge extension operator remain starlike with respect to a boundary pointw=0 on the unit ballBn?

Fortunately,we give a affirmative answer,as follows:

Theorem 3.5Suppose that

Thus we prove thatΦ[f]is an almost boundary starlike mapping of orderα.

Remark 3.6Whenα=0,Theorem 3.5 was originally due to[8]in the Loewner chain method.

3.3 Some problems

Whenα=0,Theorem 3.2 gives necessary and sufficient conditions for the boundary starlikeness of biholomorphic mappings in the unit ballBnof Cn.It is natural to ask about the proper conditions for the boundary starlikeness of biholomorphic mappings in some Reinhardt