基于D分解的分数阶PID控制器的图形化参数整定

陈思溢，牛 旭

(湘潭大学 自动化与电子信息学院，湖南 湘潭 411105)

0 引言

分数阶微积分起源于三百多年前，分数阶和整数阶相比能更精确地描述实际对象。鉴于分数阶理论的优越性，近年来对分数阶控制系统的研究愈发成为一个热点课题。特别是对分数阶控制器研究，1998年I.Podlubny教授提出的分数阶PIλDμ控制器作为经典控制器模型已成为最近分数阶领域的研究重点[1]。对于分数阶PIλDμ控制器的参数整定，取得的成果主要有：图解设计法、智能优化算法、解析设计法、D分解法等。此外，极点配置在控制系统设计的瞬态响应和鲁棒性等性能方面具有重要作用。文献[2]采用参数空间法讨论利用分数阶PIλ控制器实现时滞系统极点配置问题。D分解法最早引入自动控制系统分析过程中是有Lanzkron等人在1959年提出[3]。文献[4]利用D分解法精确地确定不确定系统的控制器参数区间范围。文献[5]运用D分解法分别描述了PD/PDμ控制器在(Kp,Kd)平面上的分数阶时滞系统的鲁棒稳定区域。文献[6-7]利用D分解法求解闭环系统的渐进稳定性问题，在此基础上确定参数空间中稳定域边界的解析表达式，并且研究了线性分数阶系统和线性参数相关情况下的D分解方法。文献[8]应用D分解法和值集的几何结构提出了一种有效的算法来计算带时滞的区间对象的鲁棒性区域。文献[9]提出了一种确定满足给定H∞优化标准的PID控制器的方法。该方法使用D分解的概念确定值集的边界，通过取区间交集来直观地描述满足要求的控制器参数范围。文献[10]通过D分解法解决低阶控制器控制高阶或时滞系统的问题。文献[11]使用D分解法求解闭环倒立摆系统的渐进稳定问题，同时文中还研究了线性分数阶系统和线性参数相关情况下的D分解方法。

本文提出了一种利用D分解法进行主导极点配置的分数阶PID控制器设计方法。其基本思想是基于动态响应指标约束来进行主导极点配置，由此可以得到分数阶控制器参数Kp,Ki关于Kd,α,β的线性函数，固定参数β后，就只有Kp和α两个自由参数。D分解法用来确定Kd和α，从而确保所选极点的优势。在此过程中，引入差分进化算法作为媒介，确定参数的稳定区域，从而使得分数阶PID控制器达到理想的系统控制性能。

1 控制系统结构

2DOF PID的概念最早由Horowitz在1963年提出的，和传统的1DOF PID相比，它较好地实现了抑制扰动和快速响应设定值变化二者之间的均衡。从本质上讲，一般情况下的单输入单输出系统理应是一个兼有设定值和扰动信号双输入且单输出的系统，使用PID控制器去控制双输入系统，本该使系统的两路性能均达到最优，然而在大部分情况下此二者不可兼得。而2DOF PID正好能较好解决这一问题，它通过引进一组无关误差的参数，使用Kp,Ki,Kd去进行扰动的抑制，再利用权重系数α,β去调整输出。

考虑如图1所示的采用二自由度分数阶PID控制策略的闭环控制系统，P(s)为被控对象，C1(s)为采用分数阶PID控制策略的主控制器，C2(s)为采用不完全微分控制策略的反馈补偿控制器，它们的传递函数形式如式(1)～(3)所示：

(1)

(2)

(3)

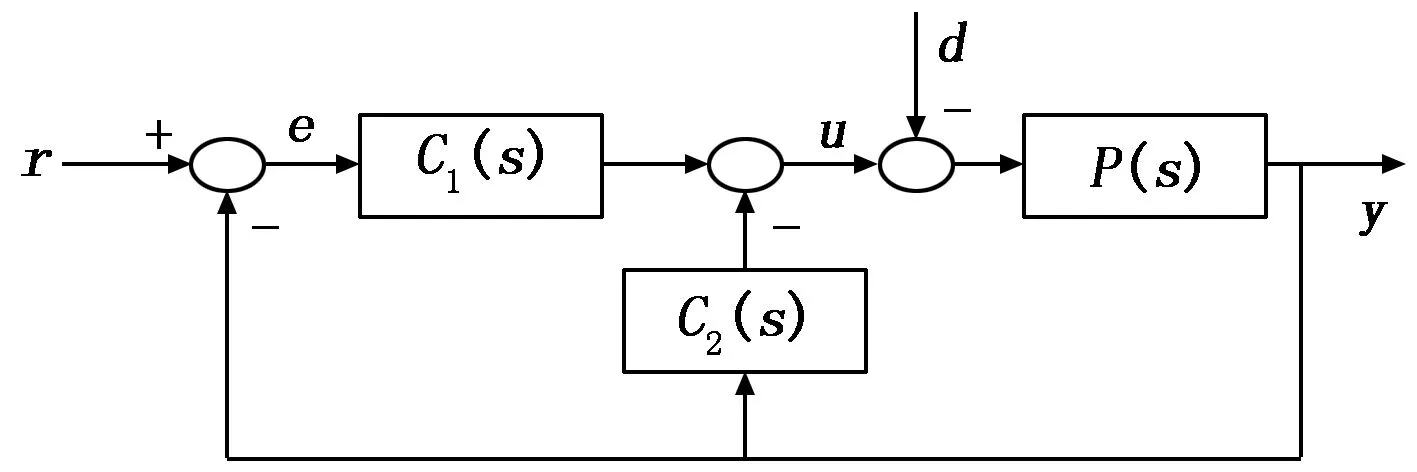
图1 控制系统结构

式中，v0,vi,vj为控制对象中的分数阶阶次，pi,nj为常数。Kp,Ki,Kd为控制器的比例、积分和微分增益，α,β为控制器中的分数阶阶次，Td为滤波时间常数。

将图1转化为具有单位负反馈形式的控制系统结构，如图2所示。其中：

(4)

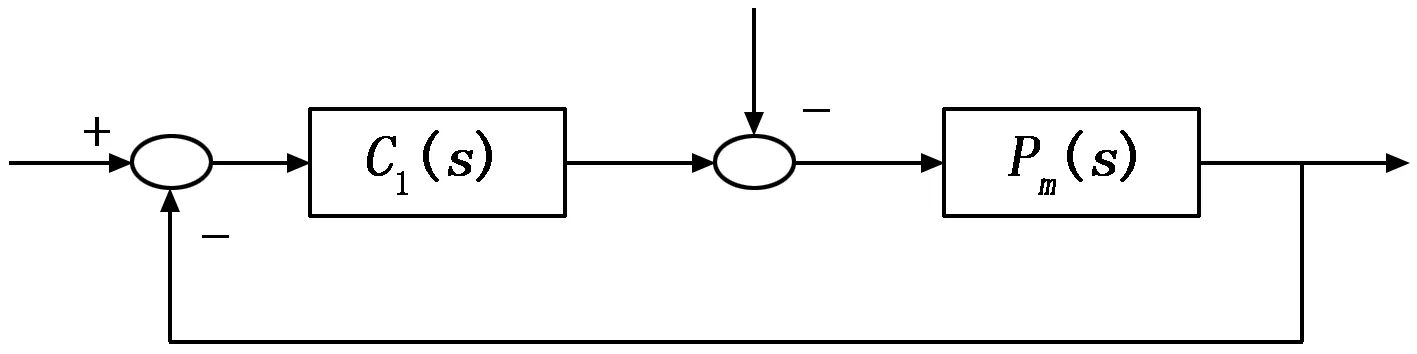
图2 具有单位负反馈形式的控制系统结构

结合式(2)和(4)，可得出图2所示的控制系统的闭环传递函数如式(5)所示：

(5)

式中：

N(s)=(Kp+Kis-β+Kdsα)(Tdsα+1)

D(s)=(Tdsα+1)Kp+(Tdsα-β+s-β)Ki+

2 基于动态响应指标约束的主导极点配置

令s=σd±jωd为系统的闭环主导极点，即闭环特征多项式D(s)的根。考虑到闭环系统的响应特性主要由主导极点确定，可根据闭环主导极点得到式(5)的近似闭环传递函数，如式(6):

(6)

考虑如式(7)的典型二阶系统闭环传递函数：

(7)

式中，ζ为阻尼系数，ωn为振荡角频率。由式(7)可得出二阶系统的动态响应指标，如式(8)：

(8)

式中，δ%为最大超调量，ts为调节时间。令式(6)和(7)中各项分别相等，可得：

(9)

联立式(8)和(9)，则可通过预设定δ%和ts解出期望闭环主导极点的位置。

将s=σd±jωd代入闭环特征多项式D(s)，并分别取其实部和虚部，可得关于Kp,Ki,Kd和α,β的多项式方程组如式(10)：

A1Kp+B1Ki+C1Kd=D1

A2Kp+B2Ki+C2Kd=D2

(10)

式中，

求解式(10)，Kp和Ki可通过Kd,α,β描述得出，如式(11):

(11)

3 基于D分解的控制器参数区域化

3.1 D分解思想

经过上一节对闭环极点配置的研究，闭环系统的主导极点可被配置在图3中由‘×’号所标识的位置，但若有其余极点同样位于图3中虚轴左侧且阴影部分右侧的位置，该对共轭极点则不是主导极点，系统的主要响应性能就无法由它得到确定。

本文采用D分解评估期望闭环极点为主导极点的真实性，它的思想如下。考虑闭环系统的稳定性，以复平面中的虚轴为界，若存在极点在其右侧，则该系统不稳定。选取控制器参数Kp,Ki,Kd,α,β，使闭环特征方程包含k个位于右半复平面的不稳定根，则定义控制器参数的变化区域为d(k)。控制器参数的变化区间可由此被划分成多个子域，其中每个都对应了固定个数位于右半复平面的不稳定根。若能寻找到一子域d(0)，则由对应的控制器参数构造得到的系统的闭环极点全部位于左半复平面，即该系统为稳定系统。

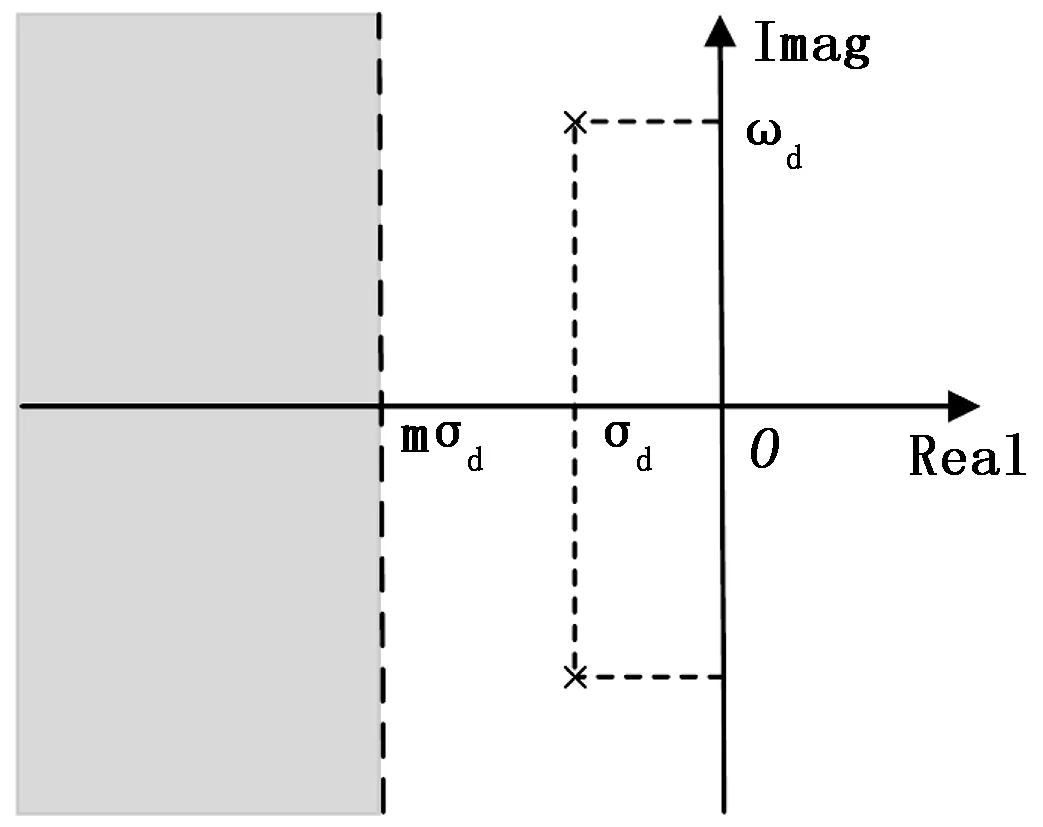
图3 闭环主导极点示意图

将D分解思想中的判别边界由虚轴替换为图3与实轴相交于mσd的虚线，其中m≥5表示系统的其余闭环极点与虚轴的距离至少5倍于主导极点与虚轴的距离。考虑此情形，在配置好期望极点的前提下，通过D分解评估得出对应控制器参数的子域为d(2)，则认为该极点为主导极点。

3.2 控制器参数区域化

改进后的D分解方法中的边界性条件可由以下两点实现：

1)D(0)=0，说明闭环特征多项式D(s)中不包含常数项，如式(12)。

2)D(mσd+jω)=0，其中ω∈(-∞,+∞)，由它即可确定图3中虚线所示的判别边界。

(12)

求解式(12)，可将Kd用式(13)描述:

(13)

由D(mσd+jω)=0，并代入式(11)消去其中的Kp和Ki，则有：

(14)

(15)

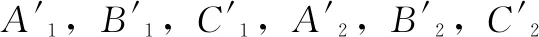
通过式(14)解出Kd，可得：

(16)

将式(16)代入式(15)，可得：

(17)

可见，在保持β一定的前提下，随着ω的变化可唯一确定α的变化轨迹，再将α代入式(13)和(16)，可进一步确定两种α与Kd之间的变化轨迹。由这两条轨迹包围而成的区域即为D分解方法中的闭环极点个数判别区域。

4 基于差分进化算法的主导极点配置

若控制器参数的整体变化区间内都不包含d(2)子域，即意味着在图3中虚轴左侧且阴影部分右侧的区域内包含两个以上的闭环极点。本文考虑子域为d(3)或d(4)的情形，对于除主导极点以外的闭环极点，利用差分进化算法在子域内寻找合适的控制器参数α,β和Kd，再根据式(11)确定Kp和Ki，从而在闭环传递函数的分子多项式N(s)中配置出复平面中位置与该闭环极点相同或相近的闭环零点，构造偶极子以消除该闭环极点带来的影响。

令s=σa+jωa为d(3)或d(4)子域中除主导极点外期望被配置出的闭环极点，则有：

D(σa+jωa)=0

N[σa+Δσ+j(ωa+Δω)]=0

(18)

式中，Δσ和Δω表示偶极子中闭环零点与极点之间的微小距离。若子域为d(3)，则意味着该闭环极点为位于[-mσd,0]区间内的负实根，此时有ωa=Δω=0。列出差分进化算法中的目标函数和约束条件如下：

差分进化算法的执行步骤如图4所示。

步骤1：对种群进行初始化，种群中的每个个体都包含5个参数：分数阶阶次α、闭环极点的实轴坐标σa和虚轴坐标ωa、以及偶极子中零极点之间间距的实轴坐标Δσ和虚轴坐标Δω。

xi,G=(σa,ωa,Δσ,Δω,α)

(20)

式中，i代表种群中的第i个个体，G代表算法的迭代次数。为兼顾算法的优化效率和运行速度，本文选择种群的总个体数量和最大迭代次数分别为30和500。

步骤2：根据式(20)中的参数，利用式(11)和(18)计算Kp,Ki,Kd，若α和Kd的取值位于D分解子域d(3)或d(4)内，则认为此时种群个体的选择满足边界约束条件。

(19)

图4 差分进化算法流程

步骤3：随机选取种群中两个不同的个体xr1,G和xr2,G，将两者的向量差按比例缩放后，与目标个体xi,G进行向量合成，得到变异个体vi,G+1，其计算过程如式(21):

vi,G+1=xi,G+F(xr1,G-xr2,G)

(21)

式中，F为缩放因子，本文中取值为1.2。

步骤4：对目标个体xi,G及其变异个体vi,G+1按一定概率进行个体间的交叉操作，从而确保变异个体中的部分信息能被传递到下一代个体ui,G+1。本文中交叉概率取值为0.8。

步骤5：将经过交叉操作得到的个体ui,G+1和原个体xi,G中的参数分别代入式(19)中的目标函数，选取适应度值较优所对应的个体，将其保留并传递至下一代xi,G+1。

5 仿真结果与分析

本文所提方法在两类控制对象上进行仿真验证，控制对象的模型如式(22)。

(22)

为验证本文所提方法的优越性，使用改进灰狼优化算法[12-14]和改进粒子群算法[15]被用来作对比，同时为了更好地对各类方法的差异进行量化分析，本文引入如式(23)的ITAE评价指标。

(23)

式中，tm表示仿真终止时间，r(t),y(t),e(t)分别表示闭环控制系统的输入、输出和误差量。

5.1 整数阶对象P1(s)

设定期望的最大超调量和调节时间分别为10%和13.92 s，根据式(8)和(9)，可解得期望的主导极点位于s=-0.368 62±j0.296 20，令滤波时间常数Td和分数阶阶次β分别为0.094 2和1.05，即可通过D分解方法将控制器参数α,Kd的整体可变区域划分为图5所示的各个子域。

图5 由改进D分解方法划分控制器参数的变化区域

图6 配置参数后的控制系统零极点图

由图6可知，经过配置参数，控制系统有一对共轭零点和一对共轭极点形成了偶极子，使系统的响应性能可以主要受到主导极点的影响。而与其他的极点或零点没什么太大关系。

以下为三类参数整定方法得到的参数结果，如表1所示，控制对象模型如式(20)。仿真结果如图7所示。

从试验结果可知,针对整数阶被控系统，本文方法在响应速度和精确度均优于改进灰狼算法及改进粒子群算法。

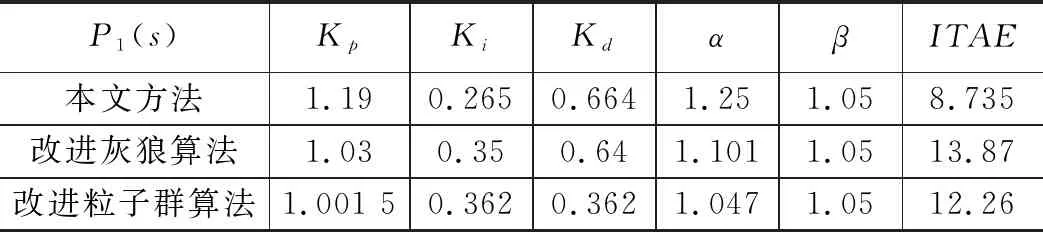
表1 各类方法的对比

图7 整数阶被控系统阶跃输出响应图

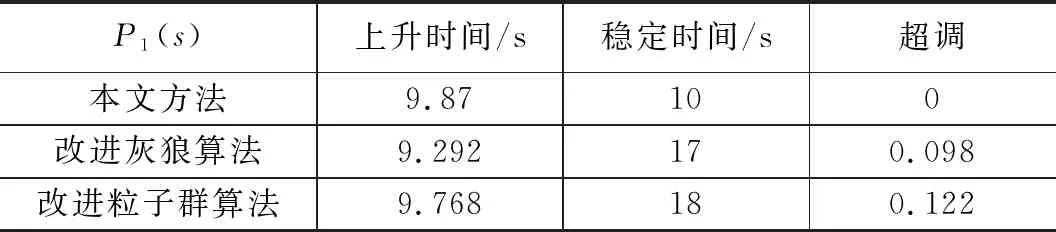
P1(s)上升时间/s稳定时间/s超调本文方法9.87100改进灰狼算法9.292170.098改进粒子群算法9.768180.122

5.2 分数阶对象P2(s)

设定期望的最大超调量和调节时间分别为3%和9.1秒，根据式(8)和(9)，可解得期望的主导极点位于s=-0.330 1±j0.943 9，令滤波时间常数Td和分数阶阶次β分别为0.094 2和1.05，即可通过D分解方法将控制器参数α,Kd的整体可变区域划分为类似图5所示的几个子域。

以下为三类参数整定方法得到的参数结果，如表3所示，控制对象模型如式(20)。仿真结果如图8所示。

表3 各类方法的对比

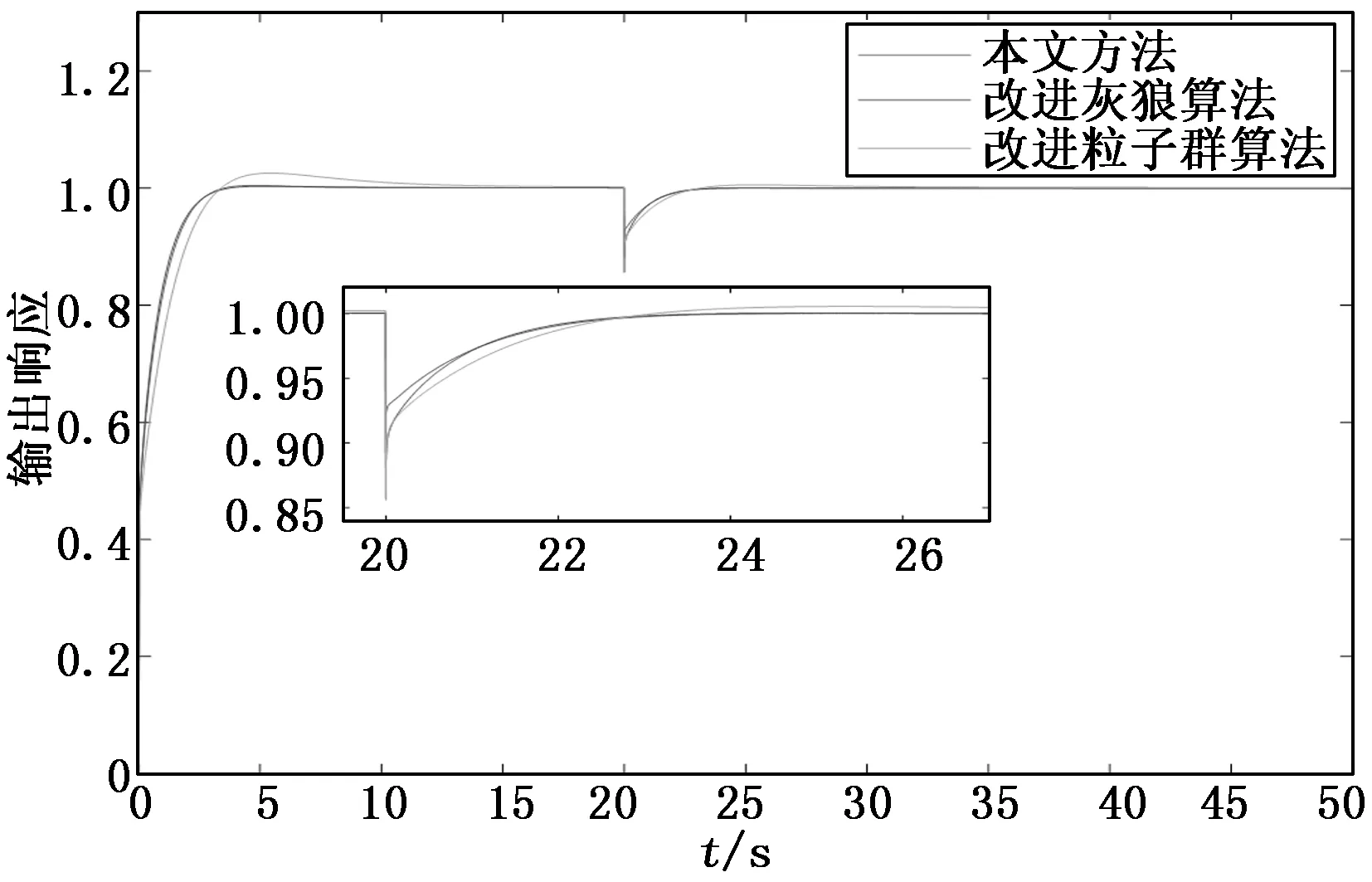
图8 分数阶被控系统阶跃输出响应图

在实验中，第20 s时加入干扰信号。从实验结果可知，针对分数阶被控系统，各项性能均优于整数阶被控系统，一定程度上也表明了分数阶控制器和分数阶被控对象结合较之整数阶被控对象的系统控制性能更优。而在三类方法对比中，本文方法和改进和灰狼算法的结果相似，同时二者在响应速度、精确度及抗干扰性能方面均优于改进粒子群算法。

6 结束语

本文提出了一种基于D分解法进行主导极点配置的2自由度分数阶PID控制器设计方法。其基本思想是基于动态响应指标约束来进行主导极点配置，以差分进化算法作为媒介，在D分解得到的稳定区域中确定最优参数，从而使得分数阶PID控制器达到理想的系统控制性能。 针对整数阶被控对象和分数阶被控对象采用三类参数整定方法设计控制器，对比实验结果显示文中所设计的方法在控制系统的快速性，稳定性和鲁棒性等方面均表现较好，由于其他两类整定方法。