基于遥测数据的浮标漂移位置建模

徐良坤 金永兴 薛晗 周世波 潘佐明

摘要：为分析厦门港主航道浮标在外力作用下的漂移规律，防止由其漂移量过大引起的船舶导航误差，根据浮标遥测位置数据，计算浮标在漂移过程中通过某一位置点的频率，建立浮标漂移位置的概率密度模型，得到厦门港主航道浮标漂移位置的概率密度分布。在此基础上分析浮标漂移位置热点区域和漂移规律。实际应用结果表明，所建立的浮标漂移位置概率密度模型可以为浮标的漂移分析提供一种新的理论方法，从而为浮标的位置维护提供有益的参考。

关键词： 浮标漂移; 概率密度; 高斯分布

中图分类号： U644    文献标志码： A

Abstract： In order to analyze the drifting rule of buoys in Xiamen Port main channel under external force， and to prevent the ship navigation error caused by excessive deviation， according to the telemetry position data of buoys，the frequency of buoys passing through a position point in the drifting process is calculated， the probability density model of buoy drifting position is established， and the probability density distribution of Buoy drifting position in Xiamen Port main channel is obtained. On this basis， the hotspot area and the drifting rule of buoys are analyzed. The practical application results show that， the probability density model of buoy drifting position can provide a new theoretical method for the deviation analysis of buoys， thus providing useful reference for position maintenance of buoys.

Key words： buoy drifting; probability density; Gaussian distribution

0 引 言

浮标为船舶安全航行提供助航服务，其位置对船舶通航安全有较大的影响。因此，确保浮标位置准确是航海保障部门的一项重要工作。水中浮标在风、浪、流以及船行波等多种外力作用下，其漂移量和漂移方向很难通过理论计算。此外，浮标在抛设时，受人的因素（由人抛投）、设备因素（卫星定位误差）、浮体姿态（浮体倾斜角）等的影响，也会造成对外发布的浮标位置与航海人员实际观测到的浮标位置有一定的偏差。因此，如何有效分析浮标的漂移，是相关航海研究人员持续关注的课题。

为分析浮标的漂移量，周春辉等[1]利用K均值聚类算法和迭代自组织数据分析算法（iterative self-organizing data analysis technique algorithm，ISODATA）计算浮标位置数据点的中心，以此作为基准点分析其他位置数据点偏离中心的距离，并构建潮流作用下的浮标漂移模型，分析浮标的漂移特点。周雨萌等[2]利用卡尔曼滤波处理浮标的遥测位置数据，在此基础上，利用K均值聚类算法和相关性分析方法建立内河航标漂移模型，进而研究长江中游武汉河段水位对航标漂移的影响。甘浪雄等[3]针对航标遥测遥控系统中航标漂移报警过多的问题，提出了一种融合卡尔曼滤波与ISODATA的方法，分析航标的漂移距离。针对浮标位置具有时间序列的特征，吳志政等[4]采用乘积季节模型建立了一个浮标漂移位置预测模型，实证效果良好。袁理等[5]介绍了一个能够在网页端使用的可视化的海上浮标漂移跟踪预测分析系统，该系统能够自动接入海洋环境数据，依据浮标参数信息，利用设定的搜救模型进行漂移模拟计算，预测浮标漂移的轨迹及最优搜寻区域。陈建亭[6]和安海伦等[7]利用浮标遥测遥控系统的远程跟踪功能实现对浮标的监控。BARBARIOL等[8]讨论了南大洋系泊平台和自由漂流平台上的波浪浮标。YU等[9]提出了一种基于东海陆架浮标数据集的漂移因子自适应修正机制。HOSTACHE等[10]研究了装有导航系统（如全球卫星定位系统）的漂流浮标，这种导航系统能够从地球上几乎任何一个点对水面高程进行准连续测量。

随着大数据时代的到来，大数据分析也应运而生[11]，URBN等[12]采用大数据评估技术，将最常用的概率密度函数拟合到每个测量点的直方图中，并用其相对对数似然进行评估。FRADI等[13]引入了高斯过程的概念，以扩展Matérn协方差函数簇。

浮标位置的概率密度分布可以作为分析浮标漂移规律的一种方法。本文根据浮标漂移可达到的水域范围，计算浮标在漂移过程中通过某一位置点的频率，建立浮标漂移位置的概率密度模型，并用浮标位置数据对模型进行验证。对浮标漂移位置概率密度分布进行深入研究，得出其概率密度分布服从高斯分布的结论。根据此结论，提出用高斯分布拟合总体的浮标漂移位置概率密度分布。

1 浮标漂移位置概率密度模型建模

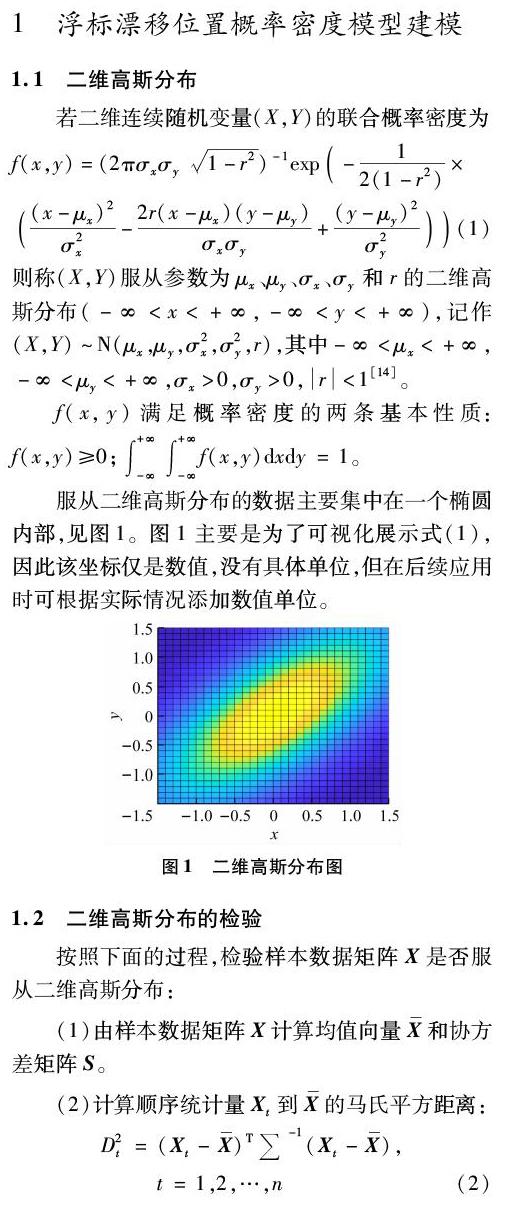
1.1 二维高斯分布

1.4 锚链长度限制

一般情况下，浮标漂移位置极限范围是以沉石为中心、锚链长度为半径的圆形水域，因此，浮标漂移位置的概率密度图不是分布在整个从负无穷到正无穷的区间，而是在上述水域范围内。因此，研究浮标漂移位置概率密度分布可以从概率论的角度分析浮标漂移规律。

2 浮标遥测位置数据及预处理

浮标的遥测数据包含浮标的位置、时间、电压等各种表征浮标运行状态的重要参数[15]。浮标的漂移轨迹用浮标位置序列表示，是一种重要的时空数据。通过对位置数据进行分析，可以得到各浮标漂移轨迹的相似特征，发现其中有意义的漂移模式。

原始的浮标遥测数据在人工输入、信息传输、传感器数据采集、存储等环节可能出现误差或错误，故须对原始数据进行预处理，获得高质量的数据集。对浮标遥测位置数据的处理主要包括两个方面：一是异常位置数据的删除，二是浮标移位后数据的挑选和清理。

2.1 异常位置数据的删除

一般来说，浮标漂失是产生异常位置数据的主要原因。根据相关统计数据，厦门港口门外航段2012—2016年浮标漂移和漂失次数见表1。[16]

浮标漂失后，回传到遥测遥控系统的位置数据与正常数据差异较大。除浮标漂失造成数据异常外，在遥测数据的传输和存储过程中也有可能产生浮标位置数据的异常。浮标异常位置数据对分析浮标漂移来说是一个干扰数据，因此需要把每个浮标的异常位置数据删除。本文将与沉石距离大于锚链长度的浮标位置数据视为异常数据予以删除。

2.2 浮标移位后数据的挑选和清理

在浮标维护过程中，由于施工或者其他原因，会对一些浮标的位置作一些小的调整。浮标位置调整后，遥测得到的数据就不再是连续数据，因而不能作为该浮标的分析数据使用。以28号浮标为例，2020年6月该浮标由原位置（24°25′46.6″N，118°03′09.3″E）调整至位置（24°25′47.5″N，118°03′04.1″E），本文采用移位前的浮标数据作为分析数据。

3 实验与分析

3.1 浮标漂移位置概率密度分布

浮标的漂移在各个方向上并不是均等的，在风、流及船行波等外力作用下，每个浮标的漂移方向会有不同的“偏好”。本文对每个浮标的活动都进行拟合和检验，数据均符合二维高斯分布的假设。

图4～10为厦门港主航道典型浮标漂移的概率密度分布图，其中颜色越深表明浮标在该位置出现的概率越大。

3.2 基于概率密度的浮标漂移热点区域位置分析

根据浮标的散点图能够分析浮标的漂移范围和风、流影响下的浮标漂移规律，但是从散点图不能看出浮标漂移位置的概率密度分布情况，即不能看出浮标漂移的热点水域或者浮标在漂移过程中出现可能性最大的区域。

对于均匀分布函数，概率密度等于一段区间（事件的取值范围）的概率除以该段区间的长度。单纯地讲概率密度没有实际的意义，它必须以有确定的有界区间为前提。可以把概率密度看成纵坐标，区间看成横坐标，概率密度对区间的积分就是面积，而这个面积就是事件在这个区间发生的概率。概率密度函数法是研究浮标漂移特性的一种重要方法，它主要通过高斯分布函数模型拟合浮标漂移位置的概率分布曲线，进而描述浮标漂移特性。总体来说，根据各个浮标位置的概率密度分布可知，浮标漂移特征可以分为以下3类：

（1）大部分浮标漂移的热点水域是在其活动水域的几何中心位置附近（4号、5号、11A号、11～15号、19号、21～24号、28号、29号浮标），如图11所示，这说明这些浮标的漂移有一定的规律性，呈现出从中心发散的特征。

（2）浮标漂移的热点水域偏离其活动水域的几何中心位置（3号、6～10号、20号浮标），如图12所示，这说明这些浮标的漂移位置不对称，浮标在风、流等外力作用下，其活动热点水域偏向于某一区域。

（3）少部分浮标漂移的热点水域在其活动水域内有多个（12A号、16号浮标），如图13所示，这说明这些浮标受外力影响的情况较复杂，外部环境作用在浮标上的力的方向和持续时间多变。

3.3 厦门港主航道浮标漂移特点分析

分析厦门港主航道各浮标遥测位置数据概率密度分布，得出主航道浮标的漂移大致有两种情况：沿主航道軸线的漂移量与垂直于主航道轴线的漂移量基本相同，例如3号浮标和12号浮标;沿主航道轴线的漂移量大于垂直于主航道轴线的漂移量，例如12A号浮标和29号浮标。

主航道内外航段浮标漂移方式的差异与港区的地理环境和水流特性密切相关。外航段水域相对开阔，厦门湾风力多为东北风和西南风，因此风对外航段浮标漂移量的影响基本不受地形条件的影响。对于内航段，12号浮标北侧的厦门岛和东侧金门岛对东北风有一定的阻挡。由于这些岛屿的遮挡，风对内航段浮标漂移的影响减弱，这使得风对外航段浮标漂移的影响明显大于对内航段浮标漂移的影响。

4 结 论

浮标位置的概率密度分布可以作为分析浮标漂移规律的一种方法，但是目前对浮标漂移位置概率密度分布的研究大多停留在定性分析阶段，定量研究较少。本文根据厦门港主航道浮标的遥测位置数据，建立了厦门港主航道浮标漂移位置的概率密度模型。对遥测位置数据进行预处理，得出了浮标漂移位置概率密度分布图，基于概率密度分布分析了浮标漂移热点区域位置，并对厦门港主航道浮标的漂移特点进行了分析总结。今后会将本文的研究成果应用到浮标的智能投放和浮标锚链配置的优化上。

参考文献：

[1] 周春辉， 赵俊男， 甘浪雄， 等. 潮流场作用下的航标漂移计算方法研究[J]. 安全与环境学报， 2021， 21（1）： 217-223. DOI： 10.13637/j.issn.1009-6094.2019.1446.

[2] 周雨萌， 初秀民， 蒋仲廉， 等. 基于卡尔曼滤波和K-means+ +算法的内河航标漂移特性研究[J]. 武汉理工大学学报（交通科学与工程版）， 2019， 43（1）： 81-85. DOI： 10. 3963/j.issn.2095-3844.2019.01.017.

[3] 甘浪雄， 徐才云， 周春晖， 等. 基于卡尔曼滤波和ISODATA的航标漂移预警方法[J]. 上海海事大学学报， 2017， 38（4）： 26-31. DOI： 10.13340/j.jsmu.2017.04.006.

[4] 吴志政， 项鹭， 肖虹， 等. 基于乘积季节模型的灯浮标漂移位置预测[J]. 电子测量技术， 2021， 44（14）： 8-16. DOI： 10.19651/j.cnki.emt.2106956.

[5] 袁理， 任虹， 鲁配仪， 等. 海上浮标漂移轨迹预测分析系统研究[J]， 航海， 2020（3）： 24-28.

[6] 陈建亭. 黑龙江航标遥测遥控系统的设计与实现[D]. 大连： 大连海事大学， 2010.

[7] 安海伦， 崔晓轩. 遥测遥控技术在航海保障领域应用的优化[J]. 航海技术， 2018（5）： 38-40.

[8] BARBARIOL F， BENETAZZO A， BERTOTTI L， et al. Large waves and drifting buoys in the southern ocean[J]. Ocean Engineering， 2019， 172： 817-828. DOI： 10.1016/j.oceaneng.2018.12.011.

[9] YU Fangjie， LI Jiaojiao， ZHAO Yang， et al. Calibration of backward-in-time model using drifting buoys in the East China Sea[J]. Oceanologia， 2017， 59： 238-247. DOI： 10.1016/j.oceano.2017.01.003.

[10] HOSTACHE R， MATGEN P， GIUSTARINI L， et al. A drifting GPS buoy for retrieving effective riverbed bathymetry[J]. Journal of Hydrology， 2015， 520： 397-406. DOI： 10.1016/j.jhydrol.2014.11.018.

[11] LI Xintong， XUE Feng， QIN Lida， et al. A recursively updated map-reduce based PCA for monitoring the time-varying fluorochemical engineering processes with big data[J]. Chemometrics and Intelligent Laboratory Systems， 2020， 206： 104167. DOI： 10.1016/j.chemolab.2020.104167.

[12] URBN A， GRONIEWSKY A， MALY M， et al. Application of big data analysis technique on high-velocity airblast atomization： searching for optimum probability density function[J]. Fuel， 2020， 273： 117792. DOI： 10.1016/j.fuel.2020.117792.

[13] FRADI A， FEUNTEUN Y， SAMIR C， et al. Bayesian regression and classification using Gaussian process priors indexed by probability density functions[J]. Information Sciences， 2021， 548： 56-68. DOI： 10.1016/j.ins.2020.09.027.

[14] 盛驟， 谢式千， 潘承毅. 概率论与数理统计 [M]. 4版. 北京： 高等教育出版社， 2008： 73-74.

[15] 艾小波. 遥测遥控技术在航海保障领域的优化[J]. 黑龙江科学， 2019， 10（20）： 108-109.

[16] 沈林华， 伊富春. 浅析开阔水域灯浮标漂移、漂失的原因及其解决方法[J]. 航测技术， 2017， 1（3）： 16-24.

（编辑 赵勉）