基于灰狼优化支持向量回归的船舶航迹预测

陈影玉 索永峰 杨神化

摘要：为提高船舶航迹预测精度，利用灰狼优化（grey wolf optimization， GWO）算法求出支持向量回归（support vector regression， SVR）模型的最优参数，构建基于GWO-SVR的船舶航迹预测模型。选取福建漳州古雷港水域某船航迹的AIS数据。将该模型与其他模型的预测结果进行比较。实验结果表明，与SVR、灰狼优化最小二乘支持向量机和粒子群优化最小二乘支持向量机等3种模型相比，GWO-SVR模型的预测精度分别提升2.61%、10.93%和0.22%，预测误差分别降低0.022、0.303和0.172。本文方法提高了船舶航迹预测精度，可为海事监管人员及时作出正确决策和保障航行安全提供支持。

关键词： 船舶航迹预测; 支持向量回归（SVR）; 灰狼优化（GWO）

中图分类号： U676.1    文献标志码： A

Abstract： In order to improve the accuracy of ship trajectory prediction， the optimal parameters of the support vector regression （SVR） model are found by the grey wolf optimization （GWO） algorithm， and a ship trajectory prediction model based on GWO-SVR is constructed. The AIS data of trajectory of a ship of Gulei Port in Zhangzhou of Fujian province are selected.The model prediction result is compared with prediction results by other models. Experimental results show that， the prediction accuracy of GWO-SVR model is improved by 2.61%， 10.93% and 0.22%， and the prediction error is reduced by 0.022， 0.303 and 0.172， respectively， compared with SVR， the GWO-least squares support vector machine and the particle swarm optimization least squares support vector machine. The method in the paper improves the accuracy of ship trajectory prediction and can provide support for maritime supervisors to make correct decisions and ensure navigation safety in time.

Key words： ship trajectory prediction; support vector regression （SVR）; grey wolf optimization （GWO）

0 引 言

為了将无人船引入商业航线，必须建立有效的避碰系统，以确保无人船自主作业所需的安全水平[1]。船舶航迹预测结果可以用来评估船舶碰撞风险，支持主动避碰，增强海上情境态势感知的能力，为船舶避碰决策提供参考。

目前船舶航迹预测方法可分为3类：基于统计模型、基于概率图模型和基于机器学习模型的预测方法。基于统计模型的预测方法有高斯回归[2]、卡尔曼滤波[3-4]和贝叶斯网络[5]等，其特点为：在建模时一般需要考虑风、流等环境对船舶运动的影响;船舶运动学方程的建立会增加模型的复杂度;随着实验的进行，误差也会不断增加。基于概率图模型的预测方法有马尔科夫模型[6]和灰色模型[7]等，其特点为：它结合概率论与图论，将不同领域的知识抽象为概率模型，将应用中的问题归结为计算概率模型变量的概率分布;灰色模型在数据量大的情况下性能较低，运行时间较长，但改进后的预测效果优于最小二乘法的预测效果。这类方法在一定程度上提升了预测精度，但还不够理想。基于机器学习模型的预测方法有循环神经网络[8]、BP神经网络[9]、长短期记忆网络[10]和支持向量回归（support vector regression，SVR）[11]等，其特点为：随着数据量的增加，神经网络可能出现梯度爆炸或梯度消失、收敛速度慢、预测精度下降以及样本训练效率低等问题;SVR需要自主选择参数，具有主观性，预测耗时短，但预测精度有待进一步提高。

随着智能优化算法的兴起和广泛应用，越来越多的研究者开始考虑引入智能优化算法到轨迹预测中。刘娇等[12]通过差分进化算法对支持向量机（support vector machine， SVM）进行优化，构建船舶航迹预测模型。这种预测方法可反映轨迹的变化趋势，但预测结果存在一定的误差，且通过差分进化算法对SVM进行优化耗时较长。SVR模型拓扑结构简单，能从未知分布的小样本中提取更多的有用信息，用来处理样本空间的非线性回归等问题，预测精度高[13]，但其预测精度显著受参数选择的影响。灰狼优化（grey wolf optimization， GWO）算法全局寻找最优解的能力较强，已被广泛用于全局优化问题中。目前，GWO算法与SVR模型的组合仅用于军用运输机航路规划[14]、材料损耗预测[15]、电力负荷预测[16]、风速预测[17]、住院费用预测[18]和入侵检测[19]等领域，还没有被运用到船舶航迹预测的研究中。鉴于GWO-SVR模型被运用到众多领域时都表现出较高的预测精度和性能，本文提出将GWO-SVR模型引入船舶航迹预测研究中，为船舶的安全航行和避碰决策提供参考。采用AIS数据作为模型样本，实现船舶航迹的准确预测。

1 船舶航迹预测理论模型

1.1 SVR模型

SVR模型建立在统计学VC（Vanpnik-Chervonenkis）维理论和结构化风险最小原理的基础上，通过回归实现经验风险和置信范围的最小化，增强学习机的泛化能力。它可以解决线性回归和非线性回归问题，在解决小样本、非线性及高维模式辨识中具有优势。

SVR的基本思想是运用一个非线性映射φ将输入向量映射到高维特征空间进行线性回归。给定一组训练数据{（x1，y1），（x2，y2），…，（xn，yn）}，其中xi为输入向量;yi为输出。

2 船舶航迹预测模型的建立

对从某港口AIS数据中提取出的航迹数据进行筛选和预处理后，将其输入预测模型，对船舶未来航迹进行预测;利用获得的预测航迹，对预测模型进行评估，验证预测模型的有效性。基于GWO-SVR的船舶航迹预测模型的实现步骤如下：

步骤1 预处理AIS数据。删去存在数据缺失和不符合实际要求的数据，得到符合要求的AIS数据。

步骤2 初始化GWO算法参数，并将其输入预测模型中。

步骤3 训练SVR模型，并计算SVR模型的函数值。此函数值表示GWO算法每次运行得出的最优解，也可理解为α狼的位置。

步骤4 调整参数值。根据SVR模型的函数值不斷更新狼群的位置和函数值，再根据这些值计算猎物位置，并对猎物进行狩猎搜索。

步骤5 判断迭代是否结束。设定GWO算法的最大迭代次数，若没有达到最大迭代次数，则不断重复步骤3～5，直至实验结束。

步骤6 输出在目标误差范围内的预测值，根据模型评估指标对其进行评估。

基于GWO-SVR的船舶航迹预测模型的流程见图2。

GWO算法与PSO算法作为群体智能优化算法，都有各自的优势。它们都能在合适的条件下满足求解精度，但PSO算法侧重于局部搜索寻优，GWO算法侧重于全局搜索寻优。它们对数据比较敏感，不同的参数设置和不同的实验数据会导致结果出现差异。

GWO算法在寻优过程中，选出最适合SVR模型的参数，从而最大化发挥SVR模型在处理小样本数据时回归拟合精度高的优势。LSSVM模型在将所有样本用最小二乘误差拟合时，计算复杂度较高;而SVR模型在通过支持向量降低LSSVM计算复杂度的同时，也具备LSSVM能够利用内核在高维度拟合样本的能力，即具有利用少量数据拟合复杂数据的能力。

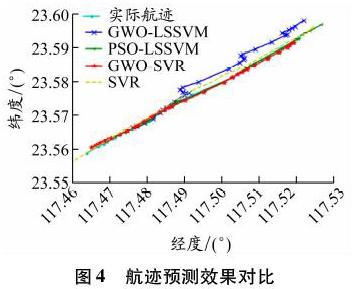
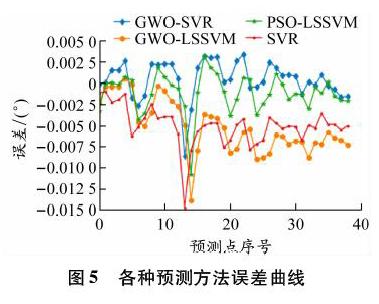
为更直观验证和评价预测结果，图5展示了这4种方法的误差。不难看出，SVR模型的误差波动最大，GWO-LSSVM模型的次之，GWO-SVR模型的误差相对于其他3种方法是最小的，且一直保持在误差为0的那条线上下波动。

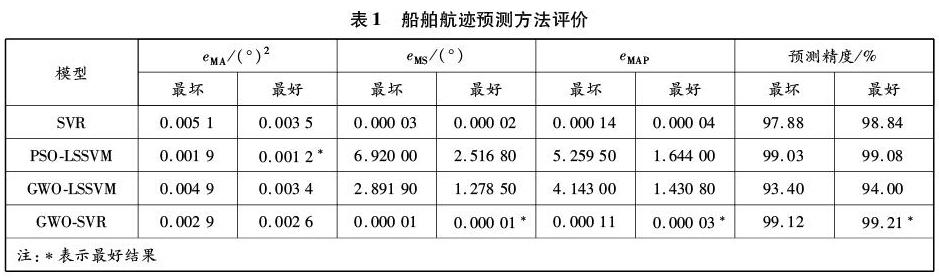
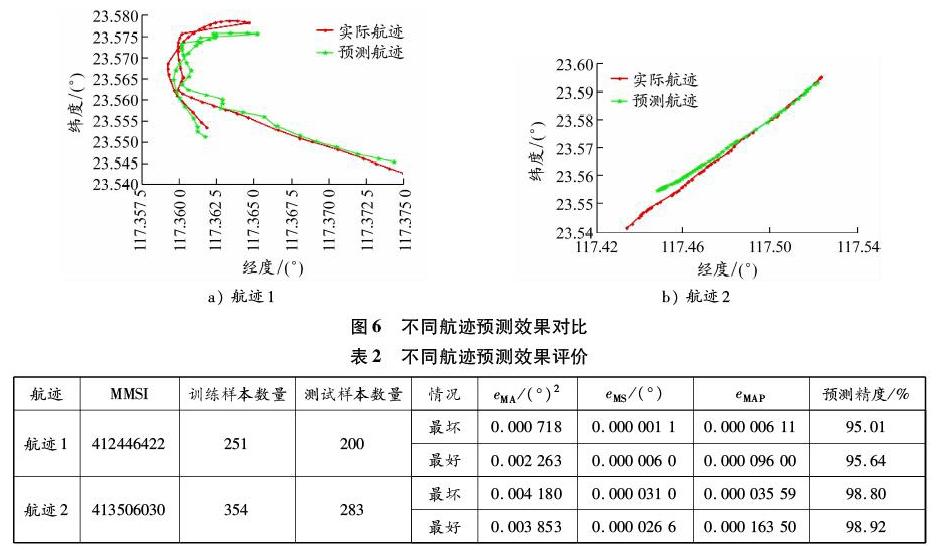
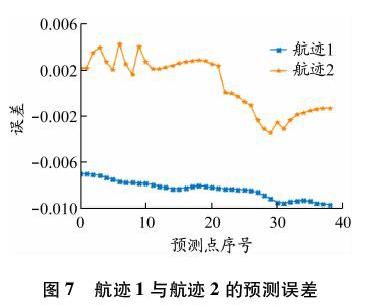
为验证模型的泛化性能，使用GWO-SVR模型对不同航迹进行预测对比。任意选择2条航迹中的部分数据进行模型训练和预测。预测航迹与实际航迹的比较见图6，航迹预测效果分析见表2，航迹预测误差见图7。

由图6可知，航迹1与航迹2均能大体反映船舶的运动趋势。航迹1由于轨迹多处弯曲，形状复杂，预测航迹点与实际航迹点之间有些许偏差，但在可接受范围内。航迹2为普通航迹，预测航迹点与实际航迹点基本吻合。

由图7和表2可以明显看出，GWO-SVR模型对其他航迹的预测效果仍然较好，误差也在可接受范围内。当航迹较复杂时，比如航迹1，SVR学习性能稍差，航迹预测结果存在一定的误差;当航迹较简单时，比如航迹2，航迹预测误差会保持在0值水平线上下波动，这种波动可能是实验数据或其他因素的影响导致的，不影响对航迹的进一步研究。综上可知，GWO-SVR模型具备一定的泛化能力。

4 结 论

结合灰狼优化（GWO）算法的全局寻优能力和支持向量回归（SVR）模型良好的回归拟合能力，通过GWO算法对SVR模型参数寻优，构建基于GWO-SVR的航迹预测模型。与SVR、GWO-LSSVM和PSO-LSSVM模型相比，GWO-SVR模型对船舶航迹的预测精度最高。先前热点研究大多关注机器学习模型，本研究将智能优化算法引入船舶航迹预测中，尝试开拓新思路解决问题。未来研究可考虑混合其他优化算法对相关机器学习模型的参数进行寻优，提高预测精度，另外，如何提高优化模型的稳定性也是值得考虑的问题。

参考文献：

[1] MURRAY B， PERERA L P. Ship behavior prediction via trajectory extraction-based clustering for maritime situation awareness[J]. Journal of Ocean Engineering and Science， 2021. DOI： 10.1016/j.joes.2021.03.001.

[2] 茅晨昊， 潘晨， 尹波， 等. 基于高斯过程回归的船舶航行轨迹预测[J]. 科技创新与应用， 2017， 215（31）： 28-29， 31.

[3] 何静. 利用卡尔曼滤波预测船舶航行轨迹异常行为[J]. 舰船科学技术， 2017， 39（1A）： 16-18. DOI： 10.3404/j.issn.1672-7619.2017.1A.006.

[4] 姜佰辰， 关键， 周伟， 等. 基于多项式卡尔曼滤波的船舶轨迹预测算法[J]. 信号处理， 2019， 35（5）： 741-746. DOI： 10.16798/j.issn.1003-0530.2019.05.002.

[5] 周巧娟. 基于贝叶斯网络的船舶航行安全性预测[J]. 舰船科学技术， 2020， 42（6A）： 34-36. DOI： 10.3404/j.issn.1672-7619.2020.6A.012.

[6] CHENG Yihang， QIAO Yuanyuan， YANG Jie. An improved Markov method for prediction of user mobility[C]//2016 12th International Conference on Network and Service Management. IEEE， 2016： 394-399. DOI： 10.1109/CNSM.2016.7818454.

[7] 劉锡铃， 阮群生， 龚子强. 船舶航行GPS定位轨迹的新预测模型[J]. 江南大学学报（自然科学版）， 2014， 13（6）： 686-692.

[8] LEE N， CHOI W， VERNAZA P， et al. DESIRE： distant future prediction in dynamic scenes with interacting agents[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition. IEEE， 2017： 2165-2174. DOI： 10.1109/CVPR.2017.233.

[9] 甄荣， 金永兴， 胡勤友， 等. 基于AIS信息和BP神经网络的船舶航行行为预测[J]. 中国航海， 2017， 40（2）： 6-10.

[10] 陈凯达， 朱永生， 闫柯， 等. 基于LSTM的船舶航迹预测[J]. 船海工程， 2019， 48（6）： 121-125.

[11] KIM J S. Vessel target prediction method and dead reckoning position based on SVR seaway model[J]. International Journal of Fuzzy Logic & Intelligent Systems， 2017， 17（4）： 279-288. DOI： 10.5391/IJFIS.2017.17.4.279.

[12] 刘娇， 史国友， 杨学钱， 等. 基于DE-SVM 的船舶航迹预测模型[J]. 上海海事大学学报， 2020， 41（1）： 34-39， 115. DOI： 10.13340/j.jsmu.2020.01.006.

[13] 李俊. 基于支持向量机的船舶交通事故预测研究[D]. 武汉： 武汉理工大学， 2008.

[14] 魏燕明， 甘旭升， 刘飞， 等. 基于灰狼优化算法的军用运输机航路规划方法[J]. 火力与指挥控制， 2021， 46（1）： 155-161. DOI： 10.3969/j.issn.1002-0640.2020.01.027.

[15] 张佳琦， 顾幸生. 基于改进灰狼算法优化的支持向量机锌耗预测[J]. 华东理工大学学报（自然科学版）， 2021. DOI： 10.14135/j.cnki.1006-3080.20210128001.

[16] 刘辉， 李侯君， 刘雨薇， 等. 基于VMD和GWO-SVR的电力负荷预测方法[J]. 现代电子技术， 2020， 43（23）： 167-172. DOI： 10.16652/j.issn.1004-373x.2020.23.038.

[17] 黄文聪， 张宇， 杨远程， 等. 模糊信息粒化和GWO-SVM算法结合的短期风速范围预测[J]. 华侨大学学报（自然科学版）， 2020， 41（5）： 674-682. DOI： 10.11830/ISSN.1000-5013.201911024.

[18] 张慧， 贺松， 张硕， 等. 基于GWO-SVR的冠心病住院费用预测[J]. 智能计算机与应用， 2020， 10（11）： 42-46.

[19] 张金霜， 梁树杰， 左敬龙. 基于GWO-SVM算法的物联网入侵检测研究[J]. 信息技术与网络安全， 2020， 39（10）： 44-48. DOI： 10.19358/j.issn.2096-5133.2020.10.009.

[20] MURO C， ESCOBEDO R， SPECTOR L， et al. Wolf-pack （canis lupus） hunting strategies emerge from simple rules in computational simulations[J]. Behavioural Processes， 2011， 88： 192-197. DOI： 10.1016/j.beproc.2011.09.006.

[21] 瘙 塁 ENAL F A， GKE F， YKSEL A S， et al. A novel hybrid PSO-GWO algorithm for optimization problems[J]. Engineering with Computers， 2018， 35： 1379-1373. DOI： 10.1007/s00366-018-0668-5.

[22] MIRJALILI S， MIRJALILI S M， LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software， 2014， 69： 46-61. DOI： 10.1016/j.advengsoft.2013.12.007.

（编辑 赵勉）