三次多项式加减速算法的应用研究
符爱周 韩震宇 葛伊伦
(四川大学机械工程学院,四川 成都 610065)
20世纪80年代末以来,计算机运行速度等性能逐渐提高,为适应市场对多样化制造产品的需求,数控系统朝着开放式趋势发展[1]。为达到开放式数控系统高速、高精的性能目标,必须保证进给速度在加工过程中变化平稳。
在数控机床加工过程中,电机启停、刀具轨迹方向变化等都会造成进给速度突变。因此,这些过程均需要进行加减速控制。根据在数控系统运行过程中的不同阶段对速度进行控制,分为前加减速控制和后加减速控制[2]。其中,前加减速控制在插补前进行,是对进给合速度控制,不会影响位置精度,但需要提前确定减速点,计算量大;后加减速控制在插补后进行,是对各轴进给速度分别控制,位置精度低,不需要提前确定减速点,计算量较小。开放式数控系统的加减速控制算法在PC机上执行,克服了计算量大的难点,为保证加工精度,本文采用前加减速控制策略,但不总是控制合速度。基于时间分割法插补原理,三次多项式的速度变化规律以及前瞻速度控制即为本文的速度控制模型。
1 基于时间分割法的三次多项式加减速控制算法简介
1.1 时间分割法插补原理概述
时间分割法是数据采样插补中的典型方法[2]。此插补算法根据进给速度和插补周期计算轮廓步长,即ΔL=V×T。其中,V为进给速度,即经过加减速控制后的速度;T为插补周期;ΔL为轮廓步长,即位移增量。时间分割法圆弧插补的基本思想是以直代曲,即用弦线或割线代替圆弧,实现微直线进给。插补计算的任务是根据轮廓步长,在已知当前节点坐标的前提下,根据曲线类型,计算下一节点的坐标。最后通过两节点的斜率,计算各轴在本插补周期内的位移增量。运动控制器根据微位移增量控制各轴电动机转动可加工出预定轨迹。
1.2 三次多项式加减速控制算法概述
在三次多项式加减速控制的速度控制模型中,速度的计算公式为三次多项式其对应的加速度为二次项,与直线、三角函数和S曲线等常用加减速控制算法相比,不会突变,故该速度控制算法有较大的柔性,适用于高速高精的开放式数控系统。但与更高次的速度控制算法相比,其柔性度还不够高。综合计算复杂度和柔性度两种因素,本文选用三次多项式的加减速控制模型。
关于三次多项式加减速控制算法本身的研究,包括具体算法的推导过程,浙江大学的冷洪滨等提出的三次多项式型段内加减速控制新方法[5]中对其进行了较为详细的叙述,本文就不再赘述,仅给出在速度控制过程中需要用到的关键公式。
在基于时间分割法的速度控制算法中,不同插补周期内的速度可能不同。这就意味着,插补周期是速度在时间尺度上变化的最小依据,即速度是离散的。速度V的离散化数学模型如式(1)。
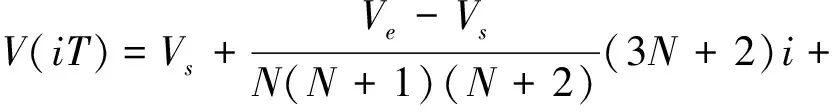
(1)
式中:Vs为起点速度;Ve为终点速度;i表示第i个插补周期;N为整数且1≤i≤N,表示加速或减速过程中总的插补次数。其中,Vs和Ve可由当前进给速度和G代码中的指令速度获得,N可由加速或减速过程中所需的时间tm除以插补周期T再取整获得,即N=ceil(tm/T),而加减速所需时间为
(2)
式中:Amax为机床的最大加速度,属于系统参数,可由选用的电动机获得。理论加减速距离Sd的计算公式为
(3)
2 常规轨迹的加减速控制
不同形状的轨迹如直线、圆弧等以及轨迹间的过渡段,在计算复杂度和加工精度的不同要求下,具体的速度控制方法存在一定的差异。下面将具体介绍数控车床中直线和圆弧两种常规轨迹以及两者之间不同组合的过渡线段的速度控制策略,即三次多项式加减速控制算法的应用过程。
2.1 直线与直线间的加减速控制
如图1,加工轨迹为两直线段OA和AB,加工方向如图中箭头所示。其中,直线OA与Z轴的夹角为α,直线AB与Z轴平行。假设OA段的指令速度为F1,AB段的指令速度为F2。
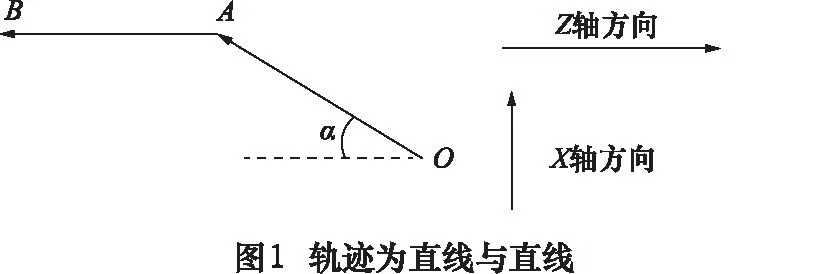
对于OA段,其速度控制过程分为3个阶段,分别为起始阶段、匀速阶段和过渡阶段。
在起始阶段,假设O点为刀具起点,则该阶段为加速阶段。其加速过程的起点速度Vs=0,终点速度Ve=F1。系统的最大加速度Amax已知,则由式(2)可得该阶段总的插补周期N1。将Vs和Ve代入(1)式可得各插补周期对应的合进给速度Vi,即
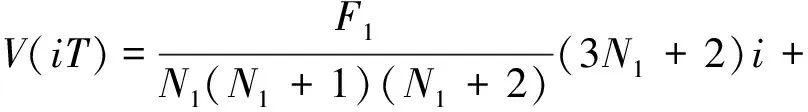
(4)
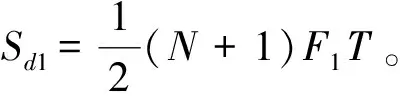
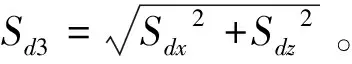
在匀速阶段,总的匀速距离Sd2=LOA-Sd1-Sd3,LOA为轨迹OA的长度,则总的插补次数N2=ceil(Sd2/F1),各插补周期对应的合进给速度为F1,X轴速度Vix=F1×sinα,Z轴速度Viz=|F1×cosα|。
对于AB段,因为在OA段的过渡阶段已将速度变化到AB段中A点速度F2,所以在该段轨迹的起始阶段不需要进行加减速控制,即没有起始阶段,其匀速阶段和过渡阶段的速度控制情况由下一轨迹段而定。
2.2 直线与圆弧间的加减速控制
如图2,加工轨迹为直线段PC、圆弧CD和直线段DE,加工方向与图中箭头方向相同。线段PC与Z轴平行,圆弧CD的首端与X轴方向相切,末端与Z轴相切,其切线与下一直线轨迹DE的夹角为α,半径为r。PC段、CD段和DE段的指令速度分别为F1、F2和F3。

对于PC段,其起始阶段和匀速阶段的速度控制算法可参照图1中的OA段。在过渡阶段,采用分速度加减速控制方法。X轴的起点速度Vsx=0,终点速度Vex=F2;Z轴的起点速度Vsz=F1,终点速度Vez=0。已知系统的最大加速度Amax,则该阶段的速度控制过程可参考直线与直线间的加减速控制部分。
对于CD段,圆弧插补以直代曲的做法导致每个插补周期对应的弦线方向都发生变化,但由于这些相邻弦线的夹角近似于180°,各轴分速度变化很小,满足速度平稳变化的要求,故不需要每个插补周期都进行加减速控制。又因为PC段的速度规划使得C点的速度等于F2,因此,CD段只有匀速阶段和过渡阶段的速度控制。考虑到在圆弧上进行拐角处速度处理的算法复杂度较高,故将该部分放在DE段的起始阶段。这就意味着,CD段只有匀速阶段,D点的合速度为F2,分速度等于该段最后一个插补周期的分速度,而与DE段的速度和斜率无关。因此,DE段的起始阶段的速度控制采用分速度控制的方法。CD段的速度计算过程如下:
设C点坐标为(Z0,X0),D点坐标为(Zn,Xn),第i个插补周期的节点坐标为(Zi,Xi)。
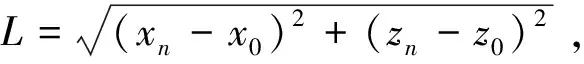
2.3 微小线段的加减速控制
在进行加减速控制的过程中,如果某一线段的长度无法满足完整的起始阶段、匀速阶段和过渡阶段速度规划所需的距离,则该线段称为微小线段。为避免程序运行出错,在调用加减速控制算法之前,需要判断当前轨迹是否是微小线段。如果是微小线段,则不能按通常的加减速控制算法对该轨迹进行速度规划,而应该根据线段的长度采取不同的速度控制策略。假设加减速控制的起始阶段、匀速阶段和过渡阶段的距离分别为Sd1、Sd2和Sd3,当前轨迹的长度为L,则存在如下几种情况:
(1)L=Sd1+Sd3:当前轨迹长度正好等于起始阶段和过渡阶段的距离之和,表明该轨迹没有匀速阶段,在进行起始阶段的速度控制后应立即调用过渡阶段的速度控制算法。
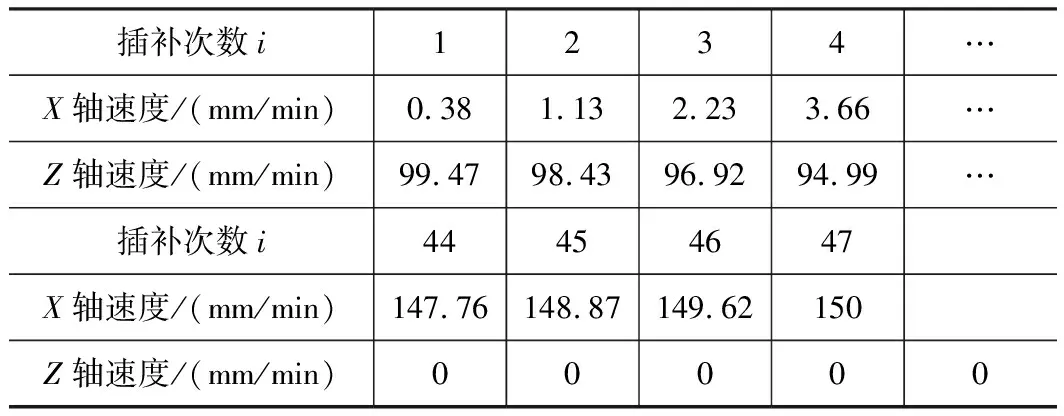
(2)L≥Sd1且L (3)L 在2.2节已经分析过,某些轨迹段不需要进行完整的速度控制过程,即未完整包含起始阶段、匀速阶段和过渡阶段。因此,在对微小线段进行速度控制时,应根据实际情况采取对应的控制策略。 综上,三次多项式加减速控制算法的应用流程如下:首先通过系统允许的最大加速度计算加减速时间,从而获得总的插补次数;接着通过轨迹长度判断是否进入微小线段的加减速控制;然后通过轨迹类型以及过渡段判断当前速度的控制阶段以及是采用合速度还是分速度控制方法;随后根据起点速度和终点速度计算各插补周期内的速度;最后根据轨迹斜率计算各轴分速度或合速度。 以图3中的零件为例,图中尺寸单位为mm,对本文研究的加减速控制算法在实际加工中的应用效果进行说明。 考虑到在本系统中,速度转换成位移的截断误差、位移转为脉冲数的量化误差以执行器的执行误差等都会造成实际的进给速度与理论速度存在差异,而此差异不会影响速度的柔性变化规律,也未能体现本文研究的速度控制策略的精度。因此,接下来的实验部分只提供仿真结果。 本系统允许的最大加速度Amax=20 mm/s2,轮廓AB的长度L=20 mm,起点速度Vs=0,终点速度Ve=100 mm/min,插补周期T=8 ms,采用2.2节的速度控制策略,可知该轨迹的起始阶段是加速阶段,总的插补次数N=32。因为该轨迹的斜率为零,Z轴进给速度等于合速度,X轴速度为零,故表1只给出该过程中不同插补周期内的部分合速度。 轨迹BC的指令速度为F=150 mm/min,轨迹AB与轨迹BC的过渡阶段采用分速度控制方法,X轴的起点速度Vsx=0,终点速度Vex=150 mm/min;Z轴起点速度Vsz=100 mm/min,终点速度Vez=0。对于X轴,该过程为加速过程,总的插补次数Nx=47;对于Z轴,该过程为减速过程,总的插补次数Nz=32。表2给出了X轴和Z轴进给速度随插补次数变化的部分结果。 表1 轨迹AB的起始阶段随插补次数变化的合速度 表2 轨迹AB的过渡阶段随插补次数变化的分速度 从表1和表2可以看出,速度随离散化的时间,即不同插补次数,平稳变化。这说明实验结果与预期相符,从而验证了基于时间分割法的三次多项式加减速控制算法的可行性。 本文研究的加减速控制算法用C++语言,借助VS2017编译环境,在Windows平台上编程实现,并最终应用在本人参与研发的开放式数控系统中。该系统控制下的三轴两联动的桌面型ET100-ZT数控装调实训车床的加工过程如图4所示。 本文在基于时间分割法原理的基础上,采用三次多项式加减速控制算法对数控机床加工过程中的进给速度进行控制,保证了速度变化的平稳性。在加工起点,采用合速度控制方法,速度按照三次多项式算法的变化规律升高或降低,保证了轮廓精度;在轨迹拐角处,采用分速度控制方法,提前预测各轴减速点,避免电机频繁启停,提高了加工效率。如果是圆弧轨迹,将其过渡阶段放到下一轨迹的起始阶段完成,在对轮廓精度影响不大的情况下,降低了算法的复杂度。此外,本文采用加减速距离与轨迹长度比较的方法对微小线段进行判断,并在下一轨迹的起始阶段继续加速或减速,解决了在微小线段上难以加速或减速到指令速度的问题。以上速度控制策略最终在笔者参与研究的开放式数控系统上应用,切实验证了算法的可行性。3 实验结果

4 结语

