再谈从矩阵位移法看有限元位移精度的损失与恢复1)

袁驷 袁全

(清华大学土木工程系，北京100084)

文献[1]通过比较杆件结构的矩阵位移法[2]和有限元法[3-4]，得出一个结论：即有限元的误差主要来自于其丢失的单元“固端解”项。其后，基于恢复单元固端解这一思想，超收敛计算的单元能量投影(element energy projection，EEP)法得以创立并取得长足发展，不仅对一维有限元法[5-8]，对二维有限元线法[9]、二维乃至三维有限元法[10-12]都建立了EEP超收敛算法，也得到了数学理论上的证明[12-13]。更有意义的是，采用EEP超收敛解替代精确解来估计常规有限元解的误差，使得基于EEP技术的自适应有限元求解得以实现，其最突出的特点是可以得到按最大模逐点满足用户给定的误差限的解答，可谓是数值精确解[14-15]。目前，这种自适应有限元方法不仅有效地应用于各种线性问题，也在特征值问题和多种非线性问题中得到了广泛而有效的应用[16-18]，而近期发展的网格局部加密技术为一类刁难奇异问题的自适应求解提供了更高性能的求解方案[19-20]。

纵观各类自适应求解，几乎都有一个共同点：因为解答事先未知，只能用后验误差方法，按照有限元求解、误差估计、更新网格三步循环迭代求解。这里的关键问题是：缺少先验定量的误差估计。这是因为，目前几乎所有的先验误差估计，都包含了事先不可计算的因素在其中，难以定量，只能是定性的。

本文作者经过对文献[1]的反思和进一步研究，发现其中的思想精华可得到更大的发扬，使得对常见的结构分析问题，有可能实现先验的定量的误差估计，从而可以不经有限元计算，便可以一举给出满足精度要求的网格划分。

本文对这一最新进展做一简要介绍，并给出初步的数值结果。作为初始探索，本文限于一维正定自伴问题的Ritz有限元法，也仅限于无内部结点的低次多项式单元。

1 方法思路

有限元的误差主要来自于其丢失的单元“固端解”项。这一结论是否准确？

下面分两种情况回答。

(1)精确单元：其形函数是齐次控制微分方程的通解，结点位移是精确的，故该结论千真万确，固端解就是精确单元内部的误差。常截面杆件矩阵位移法的单元即是精确单元，参见文献[1]中的图1：其状态(II)为有限元解，而状态(I)为固端解，亦是有限元解的误差。

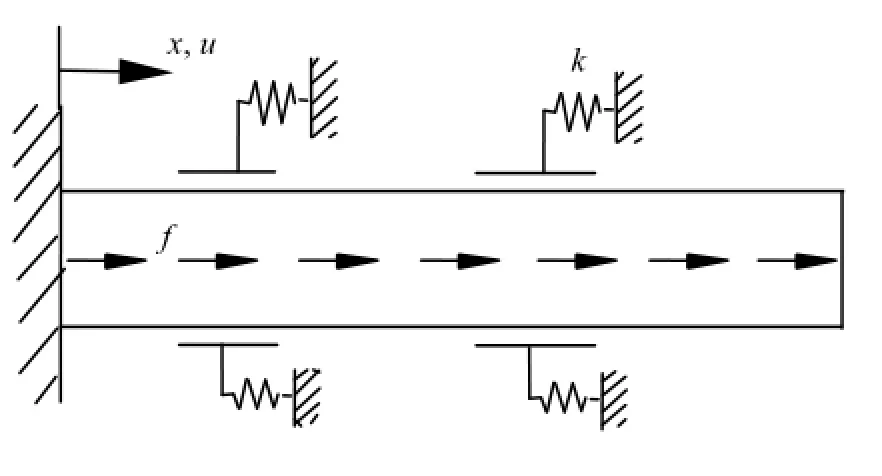
图1 二阶问题物理模型

(2)近似单元：其形函数不是齐次控制微分方程的通解，结点位移是近似的，单元内部误差由固端解和非固端的有限元解共同组成。但是，有限元的数学理论已有证明，有限元的结点位移相比于单元内部位移是超收敛的，而且具有最佳超收敛性[4]；以C0类单元为例(文献[1]的表2)，m次单元在单元内部为O(hm+1)阶收敛，而在结点上是O(h2m)阶收敛的。所以，对于近似单元，特别是高次单元，相对于单元内部位移的误差，结点位移的误差是高阶微量，可以合理地将其略去，即近似单元误差的主要来源亦为固端解。

这样，精确单元和近似单元的误差的主要来源便得到了统一，即单元的固端解项。然而，求固端解是局部单元的问题，并不需要作整体的有限元求解。这就使得不经有限元求解而预先对有限元解的误差做出定量估计成为可能，此即为本文之核心要义所在。为方便，本文将所提出的方法简称为“固端法”，以下对其做进一步的介绍。

2 模型问题和有限元解

矩阵位移法的单元涉及轴向(拉压)和横向(弯曲)变形的两种类型单元；虽然在单元上相互没有耦合，但在整体结构上有相互作用。本文仍然采用文献[1]中的两个常微分方程问题作为本文的模型问题：

(1)二阶常微分方程(轴向变形问题，图1)

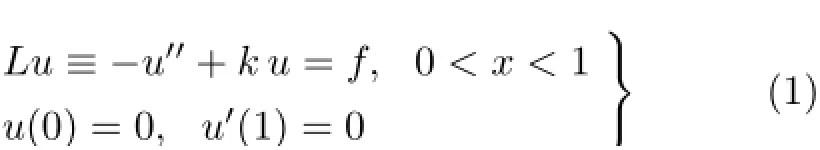
(2)四阶常微分方程(弯曲变形问题，图2)

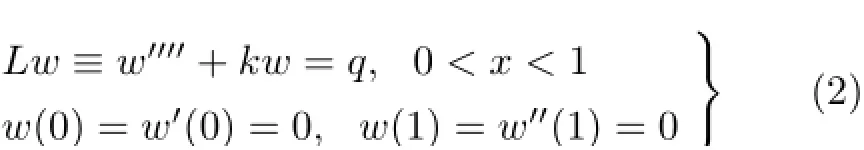
其中，L代表微分算子，u和w代表位移和挠度，k为弹性地基的刚度，f和q为均布载荷，均设为非负的常数。

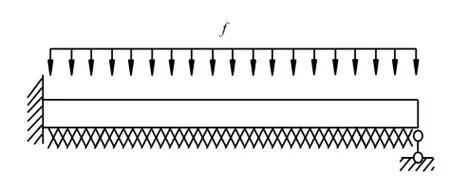
图2 四阶问题物理模型

用有限元求解时，和矩阵位移法一致，轴向问题(1)采用线性单元，其解记为uh；弯曲问题(2)采用3次Hermite插值单元，其解记为wh，在单元上分别用结点位移表示为

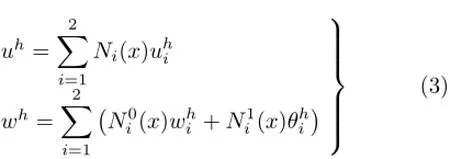
熟知，若没有弹性地基(k=0)，则两类单元均为精确单元(即矩阵位移法的单元)；而有了弹性地基(k＞0)，则两类单元都是近似单元了。

图3 和图4给出了典型的精确单元和近似单元解答的误差图，从中可以看出，精确单元结点处没有误差，近似单元结点处误差也比单元内的微小，误差主要来自单元内部，来自固端情况。

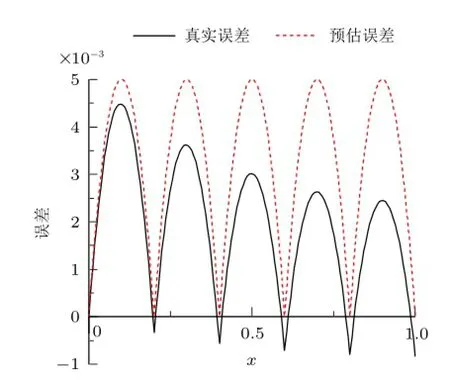
图3 例1位移误差图

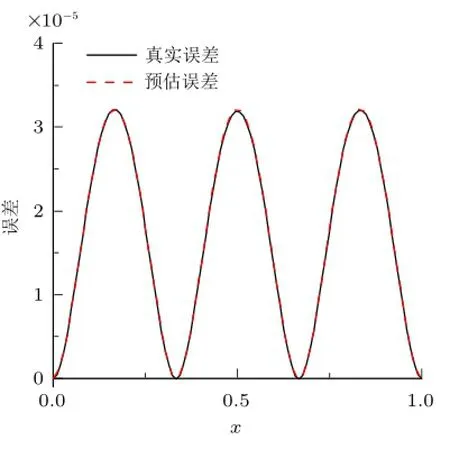
图4 例2位移误差图

3 EEP解和自适应

以上两个问题的有限元解，都已建立了EEP超收敛解的公式，可以计算单元(¯x1，¯x2)上任意一点x∈(¯x1，¯x2)的EEP超收敛解，根据本文问题直接引用如下。

(1)二阶问题[5]

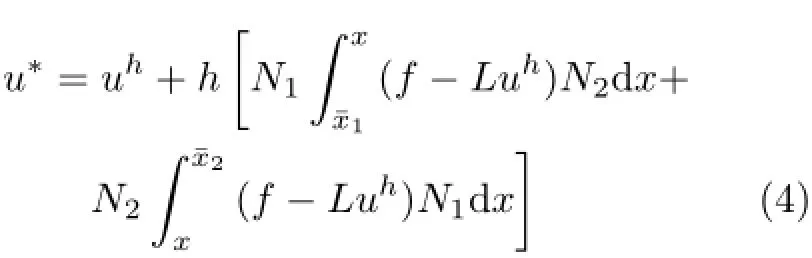
(2)四阶问题[7]

其中

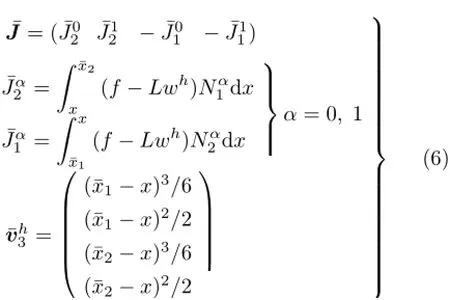
特别地，当k=0时，由于是精确单元，其结点位移是精确的，还满足Luh=0和Lwh=0。此时，EEP解亦为精确解，可以直接用来估计精确单元的误差(或计算其精确解)，计算上也更加简洁。

二阶问题

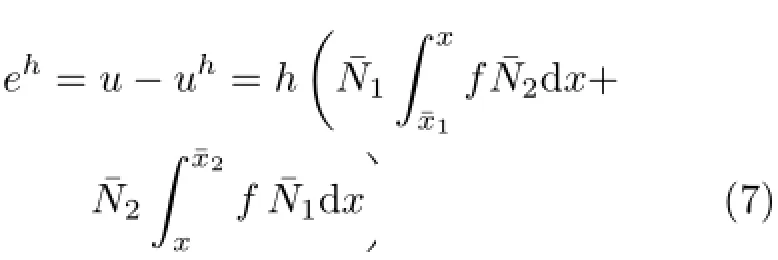
四阶问题

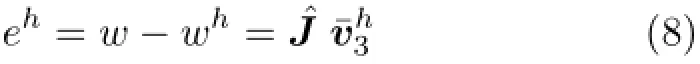
其中ˆJ的分量简化为

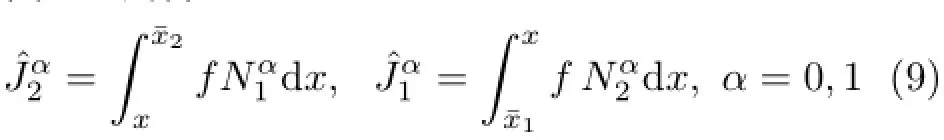
式中，eh为有限元解在单元上的误差。注意，此时的误差计算并不包含有限元解。

目前，基于EEP解的自适应有限元分析已得到长足发展。由于精确解未知，实际计算时，用EEP超收敛解代替精确解进行后验误差估计，其求解目标是：寻求一个网格使得有限元解按最大模满足给定的误差限tol，即要求满足

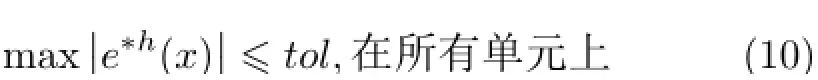
式中，e*h=u*-uh或e*h=w*-wh。这样，自适应分析就需要在初始网格上首先求有限元解，然后计算EEP解并估计各个单元的误差e*h，对那些不满足式(10)的单元进行二分，形成新网格后再次求有限元解，如此循环迭代，直至所有单元满足式(10)为止。

4 固端法

自适应过程中，最耗时的是各级网格上的有限元求解及相应的EEP解的计算，能否尽量减少、甚至避免有限元计算？并非没有可能。

为此，稍加仔细地考察一下精确单元的自适应。如前文所述，精确单元的误差完全来自固端解。参见精确单元的EEP式(7)和式(8)，不仅所计算的误差eh都是精确的，而且并没有出现有限元解uh或wh。更利好的是，对于本文的常系数和常载荷情况，精确单元的误差eh及其最大值ehmax≡max■■eh■■都可以很简单地事先算出来：

二阶问题精确单元

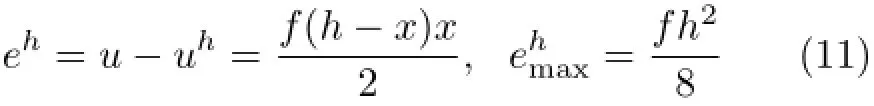
四阶问题精确单元

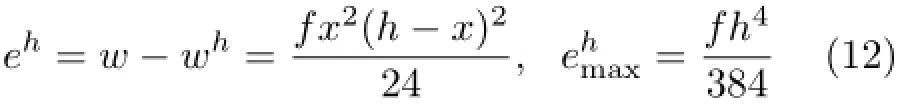
其实，以上最大误差就是结构力学中熟知的，均布载荷作用下，单元两端固定时其中点的最大位移(挠度)。这样，令ehmax≤tol，便可以一举确定出所允许的单元长度：二阶问题

四阶问题

式(13)和式(14)便可以用来直接确定单元的允许长度，而无需反复地自适应迭代计算。用单元固端解预估单元的误差并确定其允许长度，本文将其称为固端法。

由于近似单元的误差主要来源于固端解，因此固端法可以有效地应用于近似单元。定性角度看，固端法要求单元长度h足够小，以使有限元解对固端情况达到满意的精度，否则对整体结构恐难达到满意的精度。对于精确单元，固端法是精确的先验定量误差估计；对于近似单元，则是略掉了结点位移误差(高阶微量)意义下的先验定量估计。一句话，精确单元的自适应有多简单，近似单元的自适应也可以同样简单。以下用算例说明。

5 数值算例

选取与文献[1]相同的两个算例。仅采用均分网格。考虑两种问题：(1)给定单元数，用固端法预估误差，并与真实误差比较；(2)给定误差限tol，用固端法预估误差、确定网格，并用真实误差检验。算例中，统一取k=f=q=1。虽然没有单独给出精确单元(k=0)的真实最大误差，但此时预估最大误差即为其真实最大误差，可以参照，也因此没必要给出。

例1二阶问题

问题(1)的求解结果列于表1左半部，可以看出，用固端法预估的误差(h2/8)均稍大于真实误差，用来做误差估计是安全可靠的。问题(2)的求解结果列于表1右半部，可以看出，预估网格的结果都满足误差限，且真实误差均略小于预估误差。以tol=0.005为例，由式(13)可有h=0.2，恰好5个单元，其位移误差图示于图3，可直观看到逐点均满足误差限。从表1中还可以看出，取4个单元则不能满足误差限。

表1 例1二阶问题的结果

例2四阶问题

问题(1)的求解结果列于表2左半部，可以看出，用固端法预估的误差(h4/384)均稍大于真实误差，用来做误差估计是安全可靠的。问题(2)的求解结果列于表2右半部，可以看出，预估网格的结果都满足误差限，且真实误差均略小于预估误差。以tol=0.000 05为例，由式(13)可有h=0.66，理论上需要1.5个单元，实际取大于该值的最小整数，即2个单元，其位移误差图示于图4，可直观看到逐点均满足误差限。

表2 例2四阶问题的结果

6 结语

本文提出的固端法，作为先验定量的误差估计方法，可以根据给定的误差限，直接确定允许的单元长度，一举得到允许的网格划分，极大地简化了有限元误差估计的计算，大量减少自适应有限元求解的迭代步骤，并大幅提升自适应有限元求解的效率。该法在其他问题中亦获得有效的应用和推广，甚至在二维有限元中也初步显示成功，这些将另文介绍。