含软夹层砂浆试件冲击特性实验分析

王建国，罗世云，张智宇，马 军，张小华

(1.昆明理工大学国土资源工程学院，昆明 650093；2.云南省中-德蓝色矿山与特殊地下空间开发利用重点实验室，昆明 650093；3.中国有色金属工业昆明勘察设计研究院有限公司，昆明 650051)

砂浆材料作为砌体结构的粘结材料，广泛应用于山区道路、房建、矿建等工程的挡土墙浇筑及固坡施工，对砌体结构的抗冲击性能起到重要作用[1]，也常用于模拟岩石在爆炸动荷载下的力学性能[2]，研究其在动载下的力学行为有助于分析砌体结构在地震荷载[3-4]、冲击荷载[5]等工况下的响应特征。文献[6-7]基于数值模拟剥离了SHPB实验中惯性效应对砂浆材料动态强度的影响并验证了其优越性；文献[8-11]通过SHPB冲击实验分析了节理倾角、节理厚度、节理填充材料及加载应变率对水泥砂浆模拟的岩石材料动态力学性能的影响；文献[8]研究表明C30混凝土和泡沫混凝土组成的硬-软分层材料中的软介质具有很好的抗高速冲击和削波作用；文献[12]利用改进的SHPB装置研究了水泥砂浆节理面在压剪复合加载下的动态界面滑移特性；文献[13-14]按照能量观点，全面分析了矢量波通过软弱夹层的传播特性，提出一种考虑夹层内一次反射波的动力响应模型，适用于层状介质的动力响应问题分析。以上文献仅研究了单独一种砂浆类材料或硬-软混凝土分层材料的动态响应特征，然而，当低浓度砂浆作为软夹层与较高强度材料组成复合结构时，对其动力响应和抗冲击性能的研究较少。为在防护工程中充分利用软材料的吸能作用，笔者借助SHPB动力学实验装置，对含软夹层的分层砂浆材料开展不同速度的冲击力学实验，分别从动态强度特性、能量传递规律、损伤变量和破坏模式角度，对软夹层复合砂浆结构的动态响应特性进行分析，以期指导复杂动荷载条件下的防护结构选型。

1 实验设计

1.1 分层砂浆试件的制备

为省去不同尺寸试件之间的强度转换，本次静载和动态冲击实验的砂浆试件规格统一按圆柱体(100 mm×φ50 mm)设计，选择2种材料配比组合(见图1)，材料A和材料B的水泥、砂子、水的质量比分别为1∶2∶0.45和1∶4∶0.6，为3层制作，分层界面方向与试件轴向垂直，即分层角度为0°，中间夹层用水泥含量低的材料B。

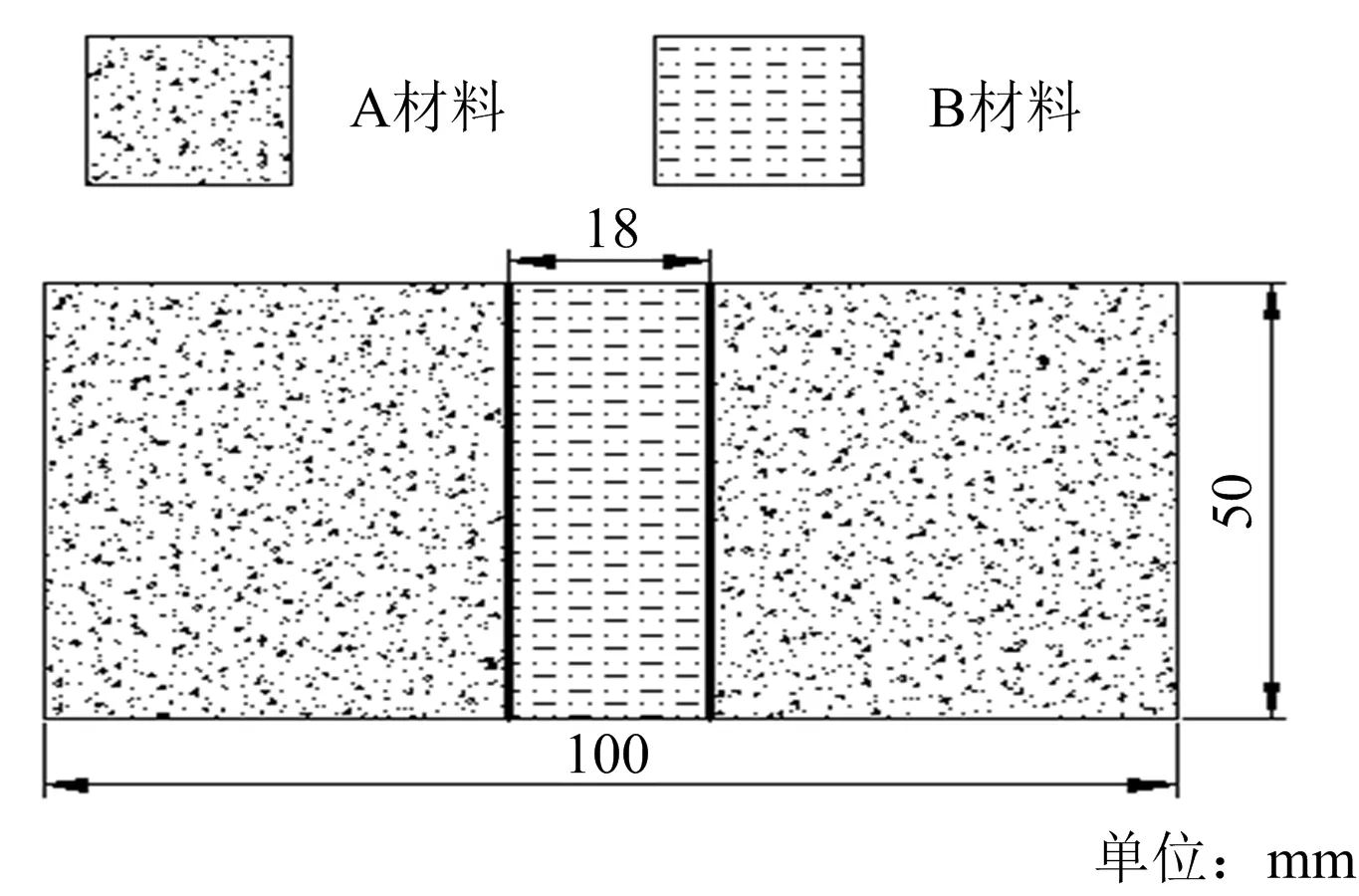
图1 分层水泥砂浆试件Fig.1 Laminated cement mortar specimens

1.2 静态单轴抗压强度

用万能实验机(见图2)对材料A、B和含夹层的砂浆试件进行静态力学参数测试，各材料的物理力学参数如表1所示。

图2 砂浆试件单轴抗压实验Fig.2 Uniaxial compression test of mortar specimen

表1 水泥砂浆材料的物理力学参数

1.3 动态冲击实验装置

分层砂浆试件动载下能量传递特性及破坏模式研究在分离式霍普金森压杆(SHPB)上完成，装置如图3所示，子弹及各杆件均为直径50 mm的钢质材料，密度7 100 kg/m3，纵波波速5 060 m/s，子弹长度0.6 m，入射杆、透射杆长2 m，吸收杆长1 m。需要强调的是，本文仅对分层浇筑砂浆试件的动态能量传递及破坏规律探究，忽略实验中试件轴向和径向的惯性效应[15]。

图3 SHPB实验装置Fig.3 SHPB experiment device

2 数据处理方法

2.1 动态强度增长因子

动态强度增长因子(DIF)已成为衡量冲击荷载下脆性材料抗压强度随应变率变化幅度的常用指标[16]，即

DIF=fc,d/fc,s

(1)

式中：fc,d、fc,s分别为试验材料的动态、静态抗压强度。

2.2 能量方程

引用文献[17]的能量计算方法，对本次SHPB试验入射波、反射波和透射波的能量按下列方程计算：

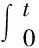
(2)

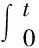
(3)

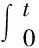
(4)

ED=EI-ER-ET

(5)

式中：EI、ER、ET、ED分别为入射能、反射能、透射能和耗散能；A0、ρ0、C0分别为入射杆和透射杆的横截面积、材料密度和弹性纵波波速；εI(t1)、εR(t1)、εT(t1)分别为入射波、反射波和透射波的应变时程曲线方程。

2.3 能量耗散比及损伤变量

依据动态加载试验测试曲线，按式(2)～(5)计算EI、ER、ET、ED，并参考文献[17]，按下式(6)～(9)计算各试件的能量耗散比n、总吸收能密度u、总耗散能密度eD和损伤变量d，并按式(1)计算动态强度增长因子DIF，结果如表2所示。

n=ED/EI

(6)

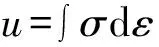
(7)

eD=ED/V

(8)

d=eD/u

(9)

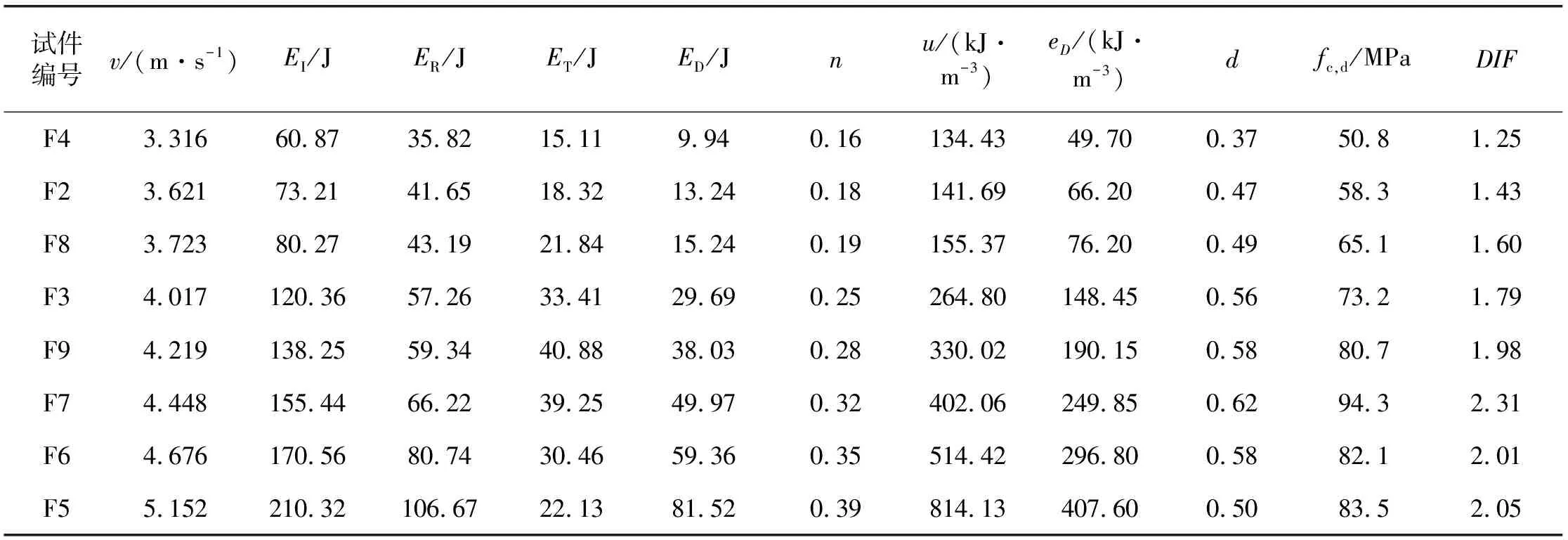
表2 不同撞击速度下夹层试件各能量及损伤变量的变化

3 结果分析

3.1 不同冲击速度下的波形曲线

实验中调整加载气压值以实现不同的冲击速度v，以3.316、3.723、4.017、4.448 m/s冲击速度(实验加载实测值)下试件的应变时程曲线为例(见图4)。由ε-t曲线可见，随着v的提高，应变波幅值逐渐增大；v从3.316 m/s提高到4.017 m/s时，透射波幅值也逐步增大，但当v继续增大到4.448 m/s时，透射波幅明显减小，反射波幅增大，说明v=4.448 m/s时，含夹层砂浆试件发生破裂与脱离，阻断了入射应力波继续往透射杆传递，以反射波的形式回到入射杆。

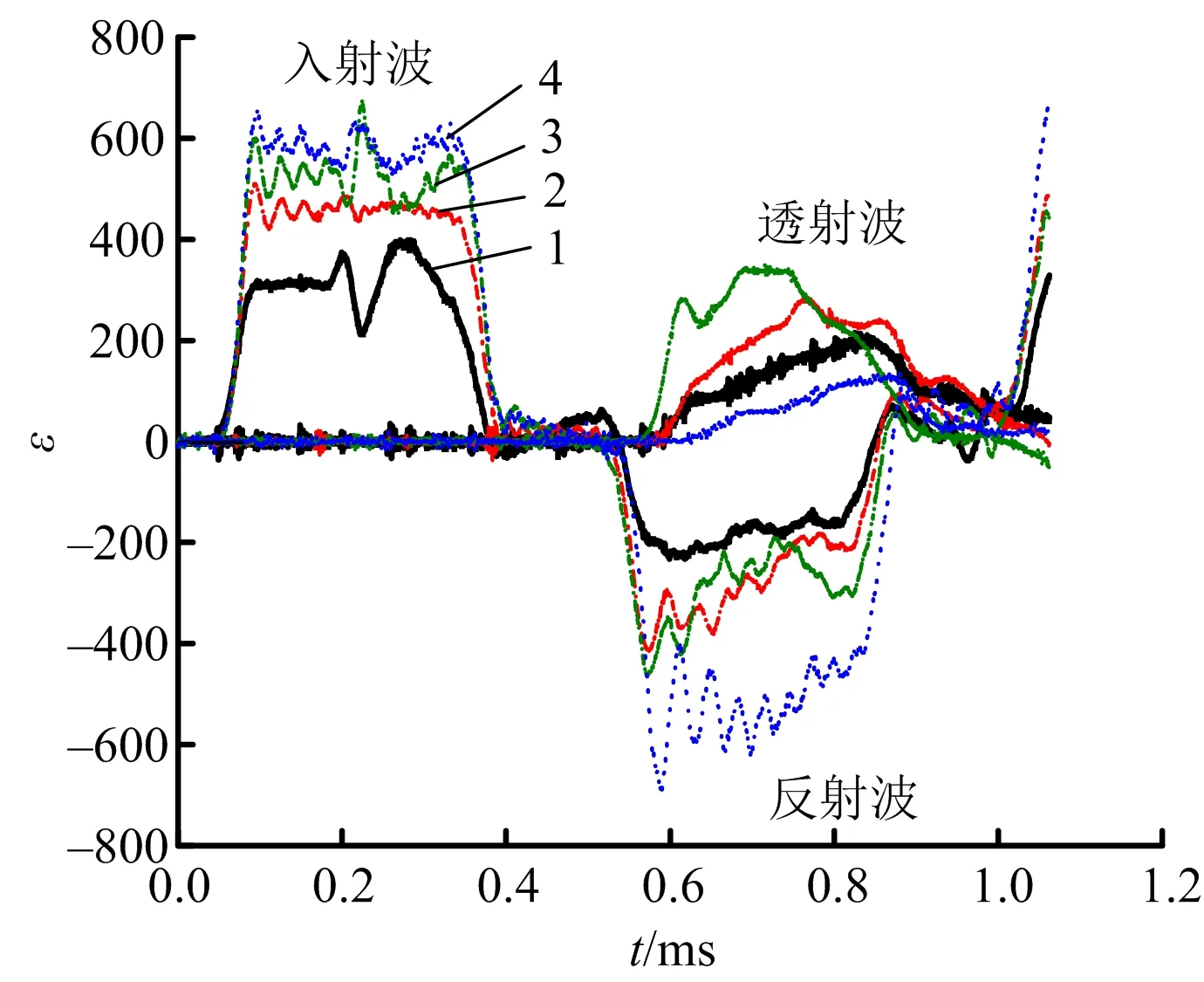
注：图中1、2、3、4分别为冲击速度3.316、3.723、4.017、4.448 m/s。图4 不同冲击速度下的ε-t曲线Fig.4 Strain-time curves under different impact velocity

3.2 强度分析

以A材料配比完整水泥砂浆试件的静态单轴抗压强度(见表1)为参量，并测试其在不同冲击速度下的动态抗压强度值，按式(1)计算动态强度增长因子DIF，与表2中软夹层试件对比，如图5所示。可以看出，到达动态峰值强度之前，含软夹层试件的DIF均小于完整试件，DIF的增加幅度也小于完整试件；完整试件在v=3.723 m/s时DIF已接近最大值，v继续增大，DIF变化幅度很小；而夹层试件在v=4.448 m/s时DIF取得最大值且大于完整试件的最大DIF值，v继续增大，DIF减小并逐步趋于稳定，但仍略大于完整试件的DIF值。说明中间软夹层对冲击作用力起到一定的缓冲作用，延缓了动态抗压强度的增长速率，将材料的抗冲击速度提高了19.5%。

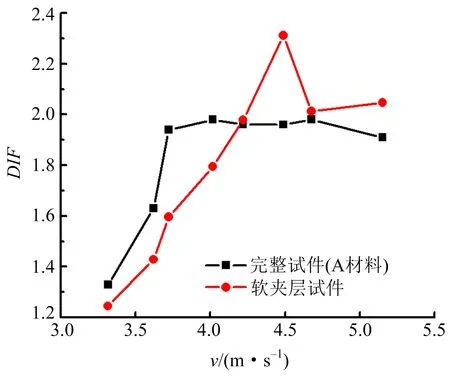
图5 动态强度增长因子与冲击速度关系Fig.5 The relationship between DIF and v

3.3 能量传递分析

由F组试件的EI、ER、ET、ED随冲击速度v的变化关系曲线(见图6)可知，EI、ED随v呈线性增长关系，ER随v呈二次函数曲线增长，ET则随v的增大先增加后减小，ER在v>4.219 m/s时增长速率加快，ET在v介于4.219～4.448 m/s之间时取得最大值，总趋势与文献[17-18]的研究结论一致，各能量随速度的变化式见式(10)。这可能是由于冲击速度大于4.219 m/s时，试件内部破裂断开，传递能量方向的介质不再紧密接触，导致反射能量增加、透射能量反而减少，耗散能呈线性增加。

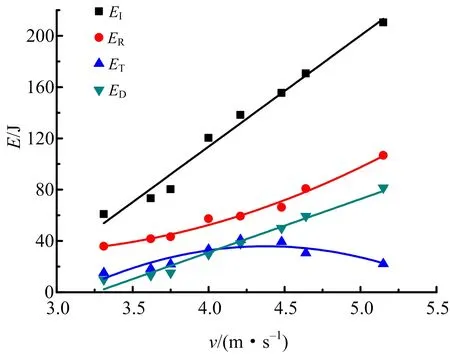
图6 不同冲击速度下各能量变化Fig.6 Each energy change with different impact velocity

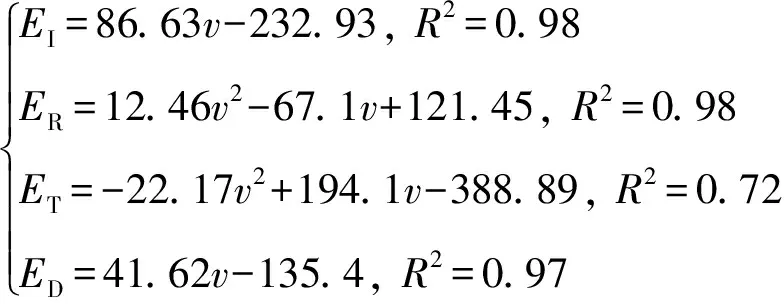
(10)

当冲击速度在3.316～5.152 m/s区间时，能耗比n随v变化呈线性增大关系(见图7)，冲击速度越大，含软夹层试件吸收的能量比越大，可见中间软夹层的吸能效果明显。

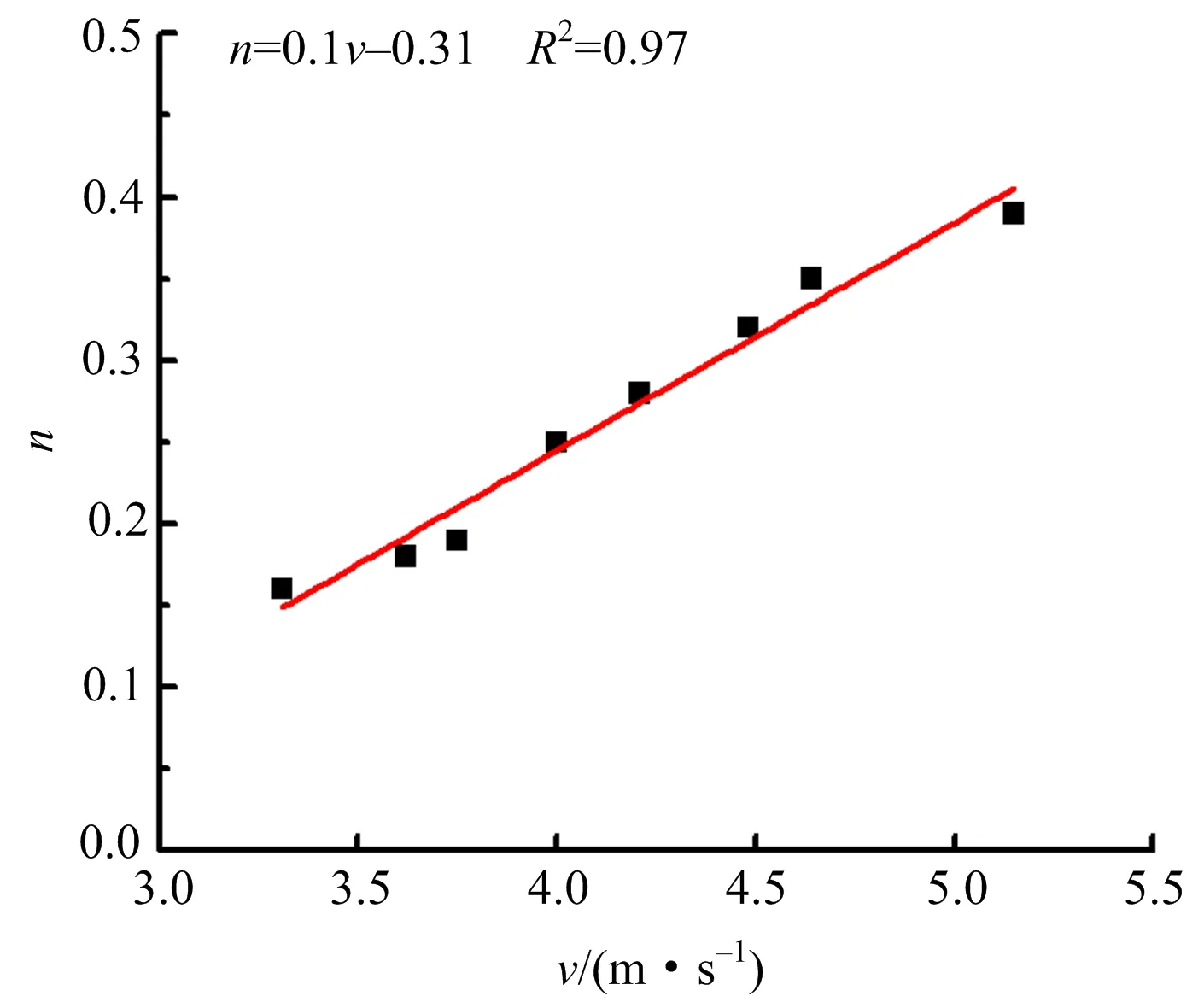
图7 能量耗散比与冲击速度关系Fig.7 The relationship between energy dissipation ratio and impact velocity

3.4 损伤及破坏模式分析

由表2中对含软夹层水泥砂浆试件的损伤变量计算结果，获得损伤变量d随冲击速度v的变化规律(见图8)。在3.316～5.152 m/s冲击速度范围内，d随v的增大先增大后减小，符合二次多项式关系d=-0.18v2+1.62v-3.0。 结合4种不同速度冲击后的试件破坏形态(见图9)，可以看出：冲击速度增至4.017 m/s的过程，d增长迅速，中间软夹层压密后裂纹增多，前段和后段依次出现贯通裂纹；v=4.017 m/s时，d=0.56，夹层试件整体沿轴向破裂成2块，且2块中均有贯穿裂纹；当v>4.017 m/s时，d增速减缓，v=4.448 m/s时，d取得最大值0.62，试件整体沿轴向劈裂破坏，软夹层破碎；速度再增加，d值减小。这是由于在4.017～4.448 m/s的冲击速度区间，中间段软弱夹层吸收了部分冲击能，破坏成多块，两端试件则沿轴向劈裂。

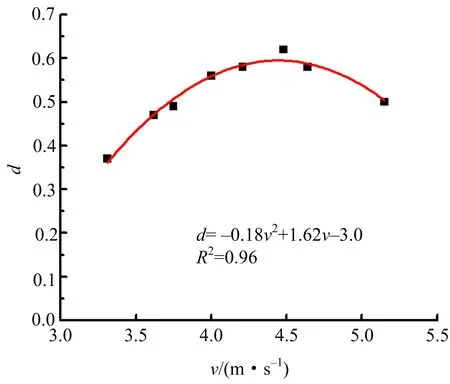
图8 损伤变量与冲击速度关系Fig.8 The relationship between damage variable and impact velocity

图9 不同速度冲击后的破坏形态Fig.9 Failure modes after impact at different velocity

4 结论

1)软夹层的吸能耗散作用明显，不仅延缓了材料动态抗压强度的增长速率，而且将其抗冲击速度峰值提高到了4.448 m/s，比完整试件的抗冲击速度能力提高了19.5%。

2)入射能和耗散能随加载速度近乎线性增长，反射能增加速率的突变点和透射能量变化的拐点发生在v=4.448 m/s附近，这是本实验设计的软夹层试件所能承受的动态冲击速度峰值，跟夹层试件的组成结构有关。

3)软夹层试件破坏时的损伤值约为0.62，损伤变量满足d=-0.18v2+1.62v-3.0，由冲击速度可确定损伤状态；反之，由破坏时的损伤变量值可确定组合材料所能承受的最大冲击速度。