壕沟地形对冲击波传播规律影响的数值模拟
徐其鹏,李芝绒,丁 刚,苏健军,刘 彦,黄风雷
(1.西安近代化学研究所,西安710065;2.北京理工大学爆炸科学与技术国家重点实验室,北京 100081)
爆炸冲击波是高效毁伤武器工作过程中的重要毁伤元,其结构和形式反映武器的威力特征和对目标的破坏程度,是高效毁伤武器威力评价、目标毁伤效能评估的重要参考依据[1-4]。而冲击波威力场的大小不仅和炸药爆热、爆压等自身属性相关,还和弹药爆炸时周围的空间场相关。Kingery等[5]在自由场中,开展了大当量范围的球形和半球形TNT炸药爆炸试验,获得了冲击波数据,并用高阶多项式拟合出了以Hopkinson-Cranz缩比率反映装药爆炸威力的经验公式。N Jacob等[6]在固支半密闭圆筒中,研究了炸药质量和爆距对圆筒结构响应的影响,以及冲击波沿半径53 mm管结构的传播规律,通过改变炸药和板之间的距离进而产生不同的载荷,并依靠板的响应将试验分为3类,在爆距小于40 mm时,爆炸载荷认为是局部的;当爆距大于100 mm时,为均布载荷。杨亚东等[7]采用镜像爆源结合线性叠加的原理研究了封闭空间长方体型结构内,爆炸冲击波的传播规律和压力分布模型,并用理论值和试验值进行了比较,最大误差不超过10.5%。陈鹏宇等[8]采用Dytran软件研究了水下接触爆炸下舷侧多层防护隔舱结构中膨胀舱的载荷特性,并在空间分布上按入射角将舱内空间划分为正反射区和马赫反射区,在正反射区,冲击波载荷由初始脉冲载荷和逐渐衰减的准静态压力叠加而成,而马赫反射区的载荷为准静态压力。庞磊等[9]用有限元分析的方法研究了城市地铁隧道车内爆炸冲击波载荷的传播特性,在车体和隧道双重空间约束下,冲击波随时间和空间的衰减速度明显降低,不再呈现传统的指数衰减规律,且波动幅度明显,加剧了车体毁坏的复杂性。倪鸿礼等[9]编制程序,采用Baldwin-Lomax代数湍流模型和TVD格式有限差分,利用PVM并行环境模拟了爆炸波在1 km以上大范围复杂地形下的传播过程,发现不同位置处冲击波峰值压力远高于用工程算法得到的值。
上述研究均考虑周围环境约束对爆炸冲击波载荷的作用效果,包括对自由场、密闭、半密闭空间、水中舱室结构及隧道等的研究。但对于野外实际作战场景,地面多为起伏不平的山坡沟壑。本文主要研究触地爆炸冲击波在不同宽度和深度壕沟地形下的传播规律,研究结果对弹药的威力性能评估及野外防御工事提高、装甲车辆及人员的安全设置防护具有重要意义。
1 数值计算
1.1 物理模型
物理模型如图1所示,地面的长×宽为1.5 m×1.5 m,55 g球形TNT炸药在距壕沟起始位置0.5 m处触地爆炸,沟长0.5 m,深度分别取0.2、0.4、0.6、0.8、1.0 m,宽度分别取0.3、0.5、0.7、0.9、1.1 m,共计11种工况(见表1)。在沿炸点与地面长度方向的0.45、0.50、0.75、1.00、1.20 m处分别布设压力测点,并依次编号1~5。
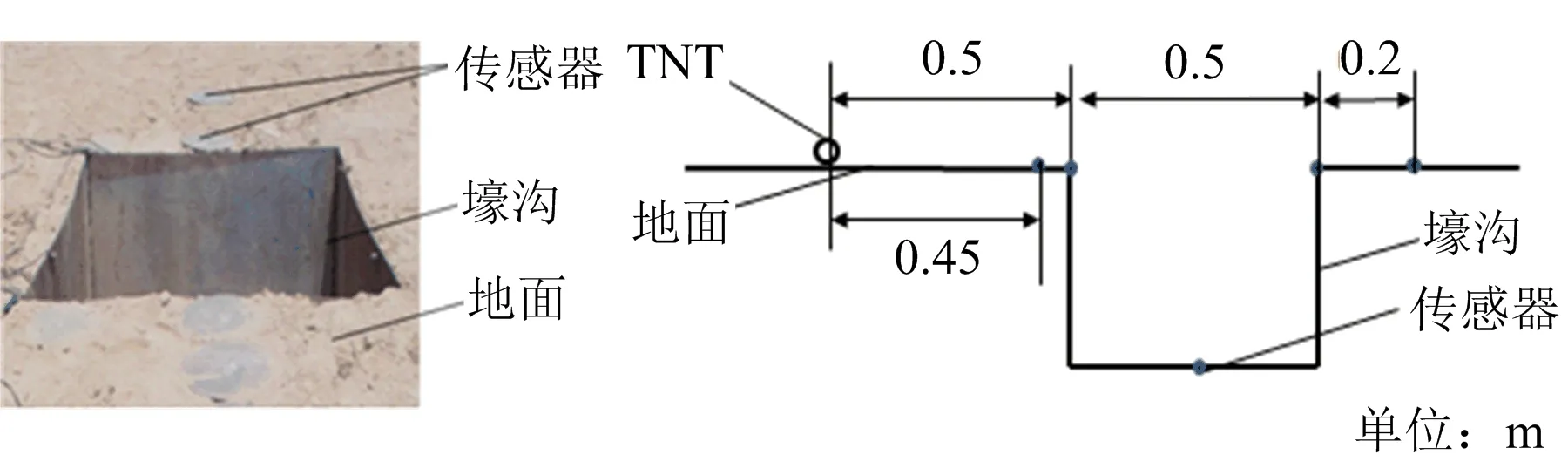
图1 物理模型及剖面Fig.1 Physical model and section
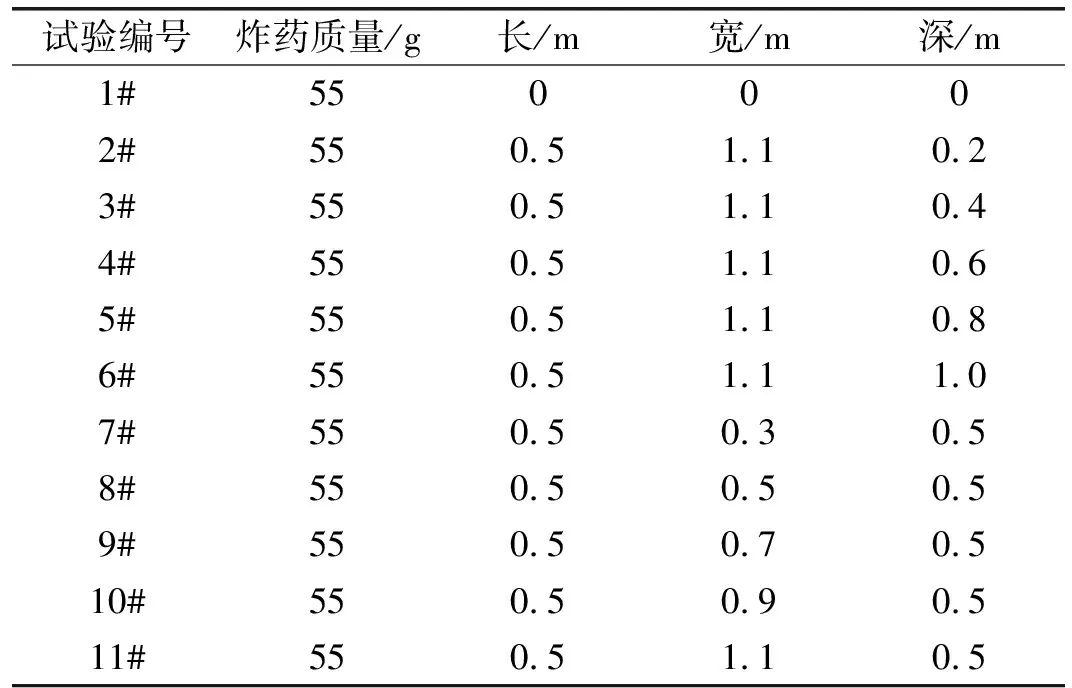
表1 试验设置
1.2 计算模型
1.2.1 网格模型及计算方法
利用Autodyn 3D进行建模和求解,考虑实际工况的对称性,建立1/2几何模型,并设置对称边界。空气域采用Euler算法,除对称面外,各边界设置流出边界条件,以模拟实际条件下的无限空气域。为了提高计算效率,利用Autodyn 2D首先进行平整地面球形装药中心起爆冲击波场的计算,然后通过FCT映射,将2D冲击波场的计算结果映射到3D空气域中。这种方法减少了炸药起爆后冲击波传播至壕沟附近的计算量和时间,也减少了Euler场的尺寸,同时更大程度保证了计算结果的准确性[10]。2D模型空气域的尺寸为0.4 m×0.4 m。为了尽可能减少计算精度带来的误差,讨论了地形区域网格尺寸对计算结果的影响。针对区域单元边长分别选取0.03、0.02、0.015、0.012 m进行对比计算,取距爆心0.5 m处的冲击波峰值压力进行对比,结果分别为72、83、92、96 kPa,可以看出,随着网格尺寸的细化,计算结果越精确,但网格尺寸为0.015 m和0.012 m的数值结果已相差不大,因此在尽可能保证计算精度的前提下,为了提高计算效率,选择网格尺寸为0.015 m。将2D模型计算的结果映射到3D空间后的数值模型如图2所示。

图2 映射后的3D计算模型Fig.2 3D computing model after mapping
1.2.2 材料模型
TNT炸药采用Jones-Wilkins-Lee状态方程描述[11-12]。
(1)
式中:p为爆轰产物压力;v为比容;E为内能;A、B、R1、R2及ω为JWL状态方程的参数(见表2)。
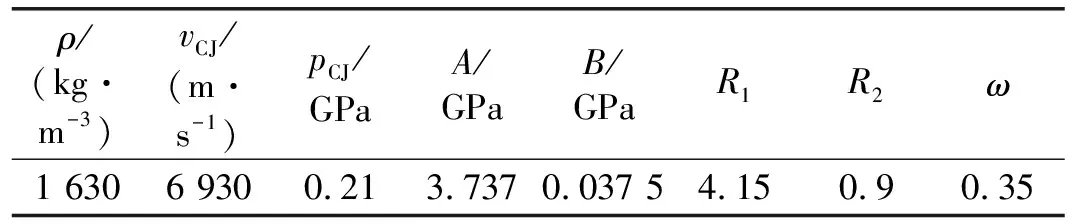
表2 JWL状态方程的参数值
空气采用理想气体状态方程描述[13-14]。
p=(r-1)ρgeg+ps
(2)
式中:p为爆轰产物压力;eg为气体单位体积内能;r为气体多方指数;ps为压力偏移量。对于空气模型:r=1.4,ρg=1.225 kg/m3,eg在mm/mg/ms单位制下取2.068×105。土壤采用刚性地面。
2 结果与分析
2.1 冲击波压力曲线的对比
1#和3#试验,测点3和5处的冲击波压力随时间变化的曲线如图3所示。从图中可以看出,由于壕沟地形的影响,位于壕沟底部中心位置测点3的峰值压力较平整地面的压力明显降低,且波形差异较大。平整地面的冲击波压力曲线呈现单一峰值,而壕沟底部的冲击波压力具有多个峰值。测点5也呈现类似的趋势,但和平整地面测点5的冲击波压力曲线差距较小。另外,壕沟底部测点的冲击波压力曲线相比平整地面的负压持续更长时间。产生这种现象的原因,可以通过壕沟地形的冲击波压力云图变化进行解释,3#试验不同时刻的冲击波压力云图如图4所示。在0.2 ms时刻,爆炸冲击波到达壕沟起始位置,开始传入壕沟底部;到1.1 ms左右,爆炸冲击波到达壕沟底部的测点3位置,形成第一个峰值压力,同时在壕沟的壁面有反射压形成;到1.6 ms,爆炸冲击波传到测点5,而在壕沟内壁面上形成了多处反射压;到2.1 ms左右,壕沟内反射压力汇聚,并再次传到测点3位置,形成第2个峰值压力。经过多次反射和能量耗散,测点3测到第3次峰值压力值已经很小了。
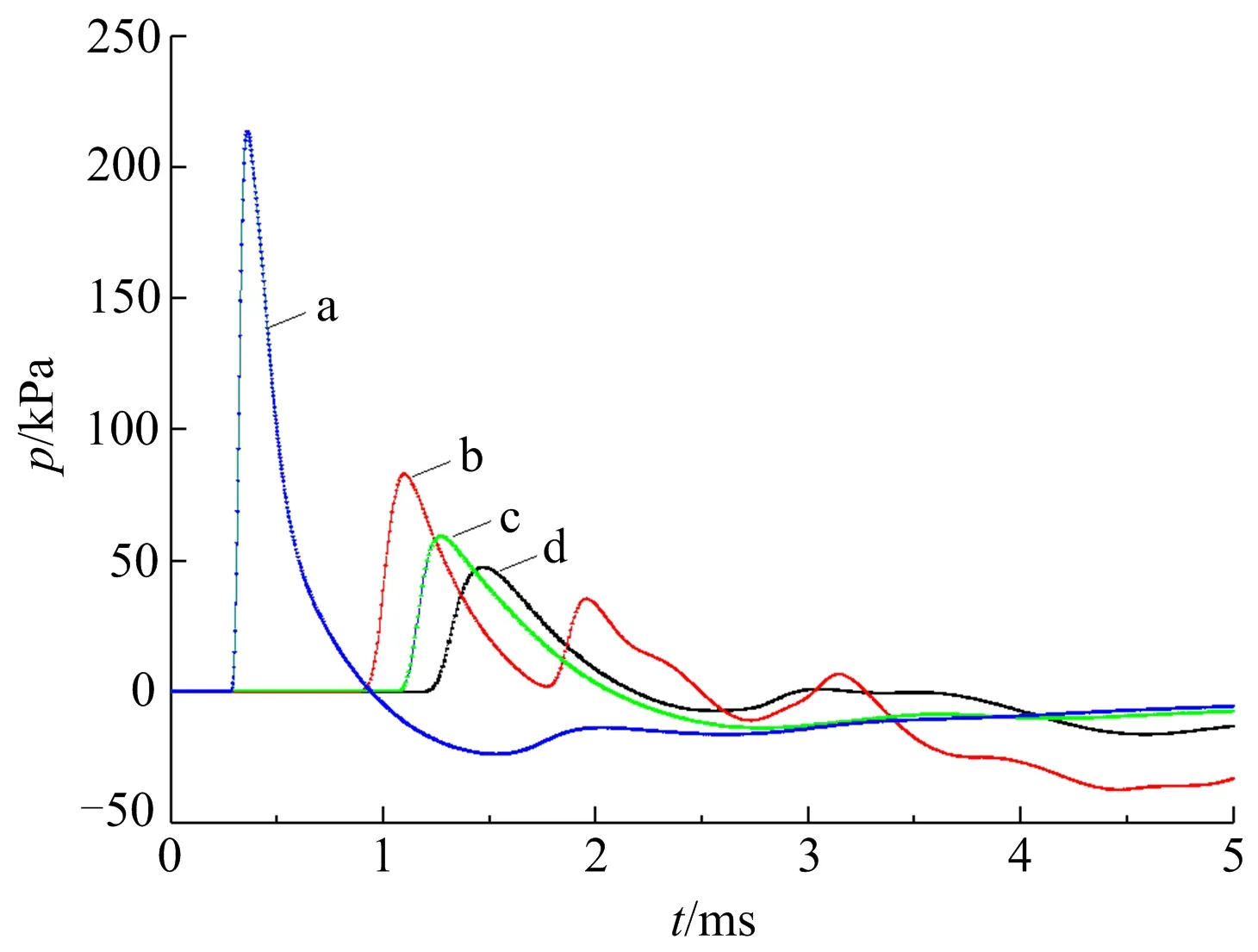
注:a、b、c、d分别表示1#试验测点3、3#试验测点3、1#试验测点5、3#试验测点5。图3 平整地面和壕沟地形冲击波压力的对比Fig.3 Comparison of shock wave pressure between flat ground and ditch

图4 冲击波随时间变化的压力云图Fig.4 Pressure cloud of shock wave with time
2.2 宽度对冲击波参数的影响
不同宽度壕沟地形,各测点的压力和冲量数据如表3所示。从表中可以看出,在到达壕沟起始位置前,测点1的峰值压力和冲量值基本保持不变;测点2处于壕沟的起始位置,由于稀疏波的快速进入,导致壕沟地形测点2处的冲击波压力和冲量相比平整地面的值大幅下降,但不同宽度的壕沟地形对测点2处的冲击波数据没有影响;壕沟底部中心位置测点3的峰值压力先降低后保持不变,当宽度大于0.7 m后,压力值维持在0.062 MPa,而冲量值逐渐降低。测点4和5处于壕沟之后,当宽度为0.3~0.5 m时,测点4的峰值压力相比平整地面的压力值稍大,当宽度大于0.7 m时,峰值压力不变。而冲量值随着宽度的增加,逐渐降低至与平整地面的冲量值一致。远离壕沟后测点5的压力和冲量值几乎不再受壕沟宽度的影响。

表3 不同宽度工况下各测点的冲击波数据
不同宽度下壕沟底部中心位置(测点3)的冲击波压力随时间变化的曲线如图5所示。
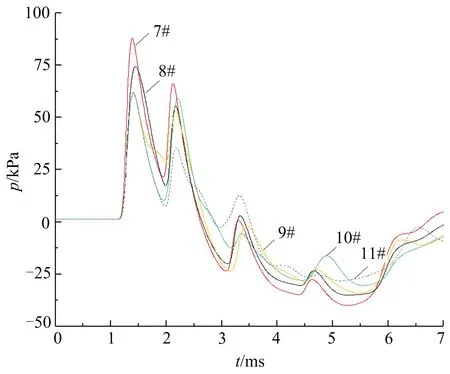
图5 壕沟宽度对冲击波压力的影响Fig.5 Influence of ditch width on shock wave pressure
从图5中可以看出,不同宽度壕沟内的冲击波压力曲线具有多个峰值,其中前两峰的压力值具有明显的意义,首峰和第2峰到达测点3的时间基本一致。随着壕沟宽度的增加,首峰压力逐渐降低,但当宽度大于0.7 m后(见10#、11#),首峰压力值基本无变化。而第2峰值压力的变化规律相对比较复杂,这是由于冲击波在不同宽度壕沟壁面的反射压相互叠加引起的。
2.3 深度对冲击波参数的影响
不同深度壕沟地形,各测点的压力和冲量数据如表4所示。从表中可以看出,在到达壕沟起始位置前,测点1的峰值压力和冲量值基本保持不变,测点2处的冲击波压力和冲量相比平整地面的值均下降,这和表3中宽度影响的结果一致。壕沟底部中心位置测点3的峰值压力随着深度的增加而降低,但冲量值则相反,当深度为0.6 m(4#)时,冲量值已经超过平整地面该处的冲量。另外,还可以看出,深度对壕沟后测点4和5的冲击波数据几乎没有影响。

表4 不同深度工况下各测点的冲击波数据
不同深度下壕沟底部中心位置(测点3)的冲击波压力随时间变化的曲线如图6所示。从图中可以看出,随着深度的增加,冲击波到达测点3的时间向后推移,峰值压力逐渐降低。当壕沟深度为0.2 m时,测点3位置冲击波的最大峰值压力为0.161 MPa;壕沟深度为0.4 m,对应的最大峰值压力为0.084 MPa,两者相差47.8%。而当壕沟深度为0.8 m和1.0 m时,对应的冲击波最大峰值压力分别是0.044 MPa和0.04 MPa,两者仅相差9.1%。所以,当壕沟深度大于0.6 m,再增加壕沟的深度,对于防护壕沟内人员或结构的意义已经不大。另外,我们还可以看出,随着壕沟深度的增加,虽然测点3位置的冲击波压力曲线保持具有多个峰值的规律,但首峰和第2峰的到达时间间隔越来越小,当壕沟深度大于0.6 m时,冲击波压力的首峰和第2峰几乎重叠在一起形成了准静态压力。
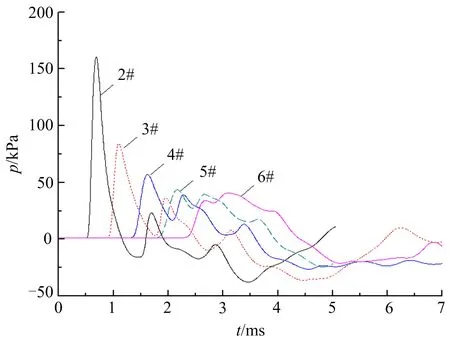
图6 壕沟深度对冲击波压力的影响Fig.6 Influence of ditch depth on shock wave pressure
3 结论
1)由于壕沟地形的影响,位于壕沟底部中心位置的峰值压力较平整地面的压力值降低,且冲击波压力曲线呈现多个峰值。随着壕沟宽度的增加,壕沟底部(测点3)的首峰压力逐渐降低,但当宽度大于0.7 m后,首峰压力值基本无变化;而第2峰压力值的变化由于不同宽度壕沟壁面反射压力的相互叠加相对复杂。壕沟底部(测点3)的冲量值随壕沟宽度的增加则逐渐降低。
2)壕沟底部的首峰压力随着壕沟深度的增加而逐渐降低,但冲量值则增加。当壕沟深度大于0.6 m后,深度对首峰压力的影响已很小,且此时,首峰压力和第2峰压力几乎重叠在一起形成了准静态压力。

