锤击震源参数对浅层地震波的影响规律研究
黄真萍,张思怡,曹洋兵,邱冬冬,张向向
(1.福州大学 环境与资源学院,福建 福州 350116;2.地质工程福建省高校工程研究中心, 福建 福州 350116;3.福州大学 国土资源部丘陵山地地质灾害防治重点实验室 (福建省地质灾害重点实验室),福建 福州 350116)
0 引言
锤击震源在浅层地震勘探方法中应用广泛,不同锤击震源产生的地震波不仅影响地震勘探采集方案设置,还对地震记录的分辨率及后续地震资料处理、解译难易程度造成影响。浅层地震勘探反射信号通常较弱,且分辨率与信噪比较低[1],优化锤击震源激发效果对于发展地震勘探技术具有重要意义。
锤击震源不仅操作方便、经济安全,且施工效率高、对各类工程场地具有普适性[2]。张保卫等[3]发现相比于夯击震源,锤击震源不仅信噪比高,且机动性更强,在浅层地震勘探中尤为适用。李文灵等[4]发现采用锤击震源进行瞬态面波勘测获取的采集结果信号较强,能够覆盖较大范围。
潘纪顺等[5]根据不同土壤条件选用金属垫板、化学垫板进行震源锤击,发现锤击时采用垫板能够获得更高的机械振动能耦合转换效率。魏德举等[6]基于层析反演的小折射表层调查技术分析重锤激发的稳定性,发现重锤激发能够显著降低施工成本,提升施工质量和效率。
为了获取更大的频带宽度和更丰富的高频信号,提升锤击震源激发效果,不少学者针对锤击震源参数对地震波的影响展开研究。现场试验方面,张陆军[7]发现选择合适的偏移距以及多次叠加的观测系统,能够增大反射波能量、保证初至结果的清晰。杨歧焱等[8]发现采用较小的道间距与偏移距有助于获得浅层的反射波信息。许新刚等[9]发现锤击震源对地表的冲击力决定了其频率组成。赵家福[10]通过对比不同质量的铁锤得到的地震波振幅谱发现增大有效波频带宽度、降低主频能够通过增加铁锤质量来实现。当锤击质量增大时,娄国充等[11]发现地震波幅值会明显增大。赵志勋等[12]通过计算不同气压下的锤击冲力统计脉宽,发现脉宽随气压增大而降低且冲力随锤击作用时间减小而增大。吴曲波等[13]则对比参数修改后地震波形记录的信噪比,得出了适合于我国西北荒漠地区地震勘探的锤击叠加次数及测线排列长度。在浅层地质勘探中,白杰等[14]分析了重锤单炮分频扫描结果,发现重锤激发的初次叠加剖面清晰连续,能够满足浅层油气勘探要求。对于深部地层的勘探, Gilmer等[15]通过改进锤击震源应用的加速度重锤震源,拓宽了锤击震源的应用范围。Kumar等[16]和孟祥顺等[17]发现加速度重锤震源经过少量次数的叠加和谱蓝化、谱整形处理后其激发地震波记录分辨率能够与炸药震源相当。为了更加高效地选取锤击震源激发参数,一些学者也针对锤击震源激发方式进行了数值模拟。Keiswetter[18]发现地震子波振幅同落锤质量、垫板面积具有较强的相关性,锤击速度和垫板质量对地震子波振幅影响不大。基于Keiswetter的研究,杨倩等[19]定量地分析土壤和岩石两种地表条件下不同锤击震源参数对激发地震子波能量和频谱的影响,得出了与Keiswetter相近的结论。詹晋等[20]基于有限元数值模型对比分析了锤击震源在不同平板材料条件下的冲击波形规律发现高强度铜合金平板在冲击中心点具有更大的冲击加速度,且信号初至清晰易分辨。刘晓宁[21]对加速度重锤震源的机械系统进行了三维建模,发现等温假设对冲击过程的动态特性研究具有可行性并推导出了冲击能量的计算方法。
纵观上述锤击震源的研究成果,发现针对锤击震源参数的研究存在以下问题:(1)虽然针对锤击震源参数对地震波的影响已有一定研究,但是针对锤击参数对激发效果的影响规律还不够清楚;(2)对于锤击震源的初始条件与边界条件的影响还有待研究;(3)大多数学者都是通过野外试验对锤击震源参数进行研究,由于试验次数有限及场地的限定,野外测量的结果不够精确,存在一定的随机性和局限性。
本文基于锤击震源激发原理,结合野外试验与数值模拟两种手段对锤击震源参数展开研究,分析大锤的质量、锤击的瞬时速度以及锤击垫板的规格3个因素作用下激发地震子波在时间域和频率域中的变化特征,研究它们对地震子波振幅、频率产生的影响,使得激发地震波的正反演过程各参数对地震子波产生的影响能够得到更为准确的分析,为浅层地震勘探优选各锤击震源参数提供依据。
1 锤击地震波影响因素的试验研究
1.1 地震波波动方程
锤击震源通过人工或机械将重锤升至一定高度令其自由落体激发地震波。将锤击震源激发地震波过程简化为一维单元中受点荷载作用下单元dx内产生应力波的过程。基本公式如下:
(1)
已知,
(2)
式中,c为波速,E为弹性模量,ρ为密度,将式(2)代入(1)中,可得单元dx的一维波动方程:
(3)
上述的一维波动方程推导过程中,在大锤与垫板接触的瞬间,忽略摩擦损失的能量,大锤的机械能E1一部分转换为落锤的动能,一部分转换成下传应力波的能量,因此E1的大小与落锤的质量和速度存在联系。另外,锤击时采用垫板可以通过增加垂直叠加次数提高信噪比,减少对地表介质的破坏,而不同规格垫板的震动对地震子波能量和频谱信号产生的干扰不同。故大锤的质量、锤击垫板的瞬时速度及垫板规格可能对锤击产生应力波的能量造成影响。
1.2 场地概况及试验流程
试验场地选择在福州平原地区,该地区地基土层是典型的软土地基,是浅层地震勘探中最为普遍的场地形式[22]。场地地面平坦,表层土为根植土(主要为黏性土),厚度约为0.5~2.0m,往下分别为粉质黏土、淤泥、粉质黏土、淤泥质土、粉砂、卵石、残积粘性土、全风化花岗岩、强风化花岗岩、中风化花岗岩等。
现场的锤击地震波勘探试验采用SWS-5多功能工程地震仪收集地震数据。按照地震波采集方法布设观测系统,设置偏移距为5m,采集道数为12道,道间距为1m,采样间隔为1ms,每道采样点数为1024。同一研究参数设置取3次试验平均值,消除误差。具体试验方案如下:
(1)研究大锤质量对地震子波的影响时,通过4种不同质量的大锤(5kg、10kg、15kg、30kg)以相同的高度(1m)经过自由落体运动锤击长度、宽度和厚度为20cm×20cm×0.5cm规格的垫板。
(2)研究垫板大小对地震子波的影响时,使用同样质量的大锤(30kg)分4组进行锤击:直接锤击根植土层;锤击10cm×10cm×0.5cm垫板;锤击15cm×15cm×0.5cm垫板;锤击20cm×20cm×0.5cm垫板。
(3)研究锤击速度对地震子波的影响时,令30kg的大锤在不同高度(0.5m、1.0m、1.5m)下落。锤击20cm×20cm×0.5cm规格垫板,通过位移与速度的关系式可计算得出0.5m、1.0m、1.5m 3个高度对应的瞬时速度分别为3.13m/s、4.43m/s和5.42m/s。
1.3 试验结果分析
1.3.1 大锤质量对地震子波的影响
改变大锤质量得到的锤击激发地震子波频谱中的主频、最大振幅及频带宽度如图1所示。

图1 不同大锤质量对地震子波的影响Fig.1 Influence of different mass of hammer on seismic wavelet
由图1(a)可知,随着大锤质量的增大,地震子波的主频和频带宽度逐渐减小,当大锤的质量由5kg增至30kg时,主频的总降幅约为21.43%。其中,由5kg至15kg每增加5kg相比前者主频降幅分别为7.13%、7.6%,由15kg增至30kg主频降幅为8.3%,说明主频随单位大锤质量的增加,降幅百分比趋于减小,最终趋向稳定。频带宽度的总降幅约为71.39%。由5kg至15kg每增加5kg相比前者频带宽度降幅分别为12.21%、10.5%,由15kg增至30kg频带宽度降幅为63.59%,说明随单位大锤质量的增加,频带宽度降幅百分比先趋于减小,后趋于增大。由图1(b)可见,经过傅里叶变换之后的地震子波最大振幅,基本与锤击质量呈线性相关。当大锤质量由5kg增至30kg时,最大振幅总增幅为479.6%。根据主频信号和振幅的大小可得出大锤质量越大,产生的低频信号的能量越大。魏德举等[6]研究认为在激发能量与重锤质量之间存在正比例关系,这与本试验结论基本一致。
1.3.2 垫板大小对地震子波的影响
改变垫板大小进行锤击,激发地震子波频谱中的主频、最大振幅及频带宽度如图2所示。
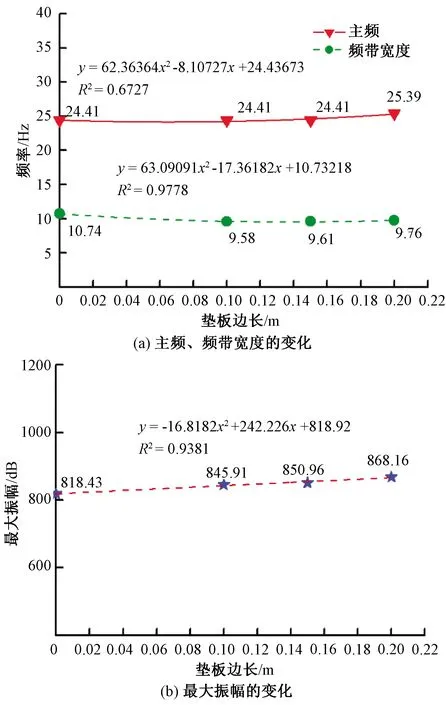
图2 不同规格垫板对地震子波的影响Fig.2 Influences of different dimension of sole plate on seismic wavelet
由图2(a)可知,主频的频带宽度集中在9.58~10.74Hz,直接锤击根植土频带宽度值最大,达到10.74Hz;锤击垫板边长由0.1m增至0.2m时,频带宽度的增幅仅为1.88%。由图2(b)可见,经过傅里叶变换之后的地震子波最大振幅,也随着锤击垫板边长增加。从无垫板到20cm×20cm×0.5cm规格垫板,最大振幅由818.43dB增至868.16dB,增幅极小,仅为5.73%。Keiswetter[18]认为垫板规格对频带宽度不会产生太大影响,这与本文试验结果基本一致。
1.3.3 锤击速度对地震子波的影响
改变瞬时锤击速度进行锤击,激发地震子波频谱中的主频、最大振幅及频带宽度如图3所示。
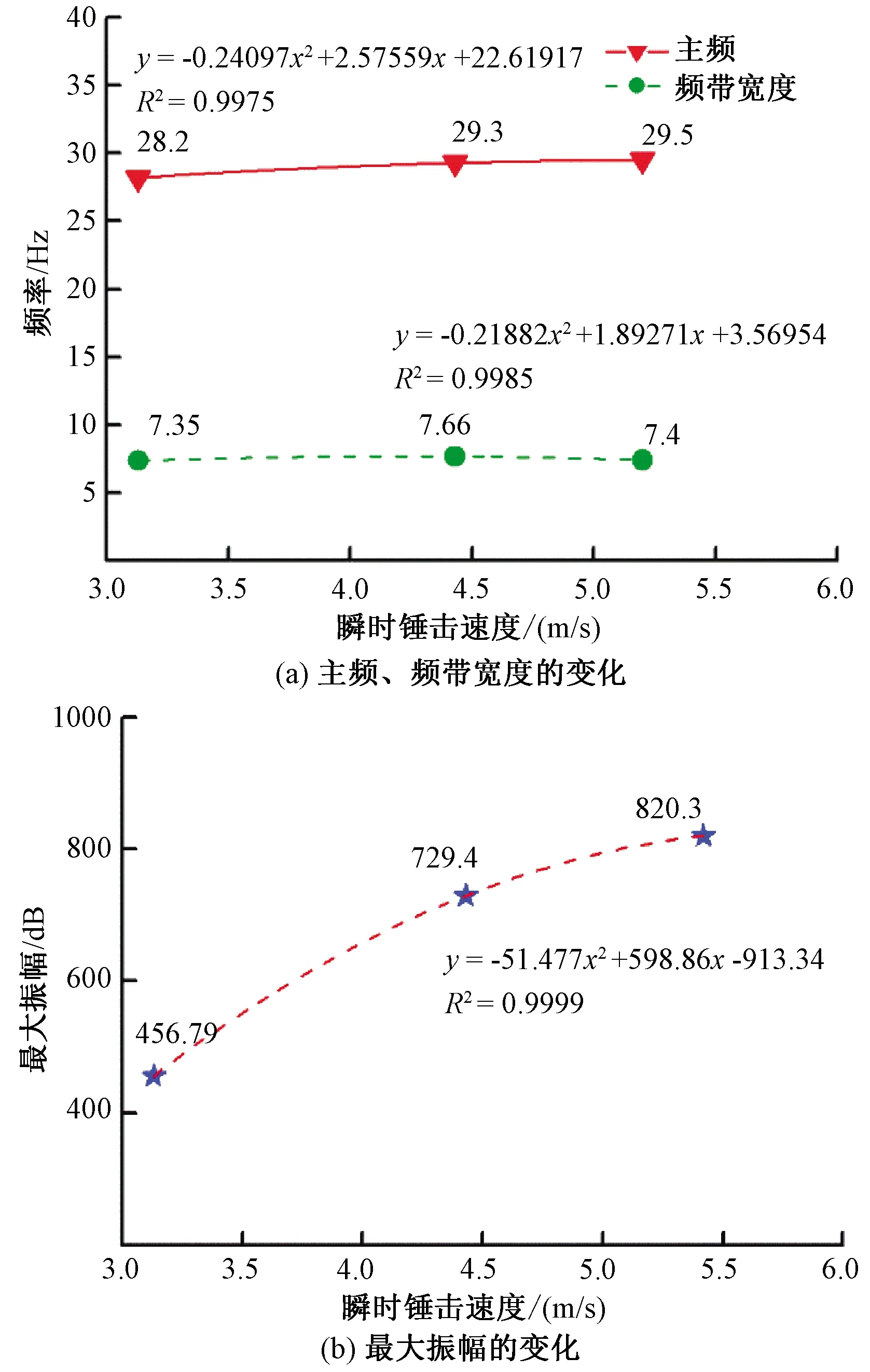
图3 不同瞬时锤击速度对地震子波的影响Fig.3 Influences of different velocity of hammer striking on seismic wavelet
由图3 (a)可知,当锤击垫板的瞬时速度由3.13m/s增至5.42m/s时,激发地震子波的主频由28.20Hz增至29.50Hz,增幅约为4.60%。频带宽度的变化较小,最大值与最小值仅相差0.26Hz。由图3 (b)可见,最大振幅由456.79dB增至820.3dB,增幅约为79.58%。其中由3.13m/s增至4.43m/s,最大振幅增幅为59.6%,由4.43m/s增至5.42m/s,最大振幅增幅为12.4%,说明最大振幅增幅速率随瞬时锤击速度增加趋于减小。锤击垫板瞬时速度对激发地震波主频和频带宽度的影响不大,仅对最大振幅产生较大的作用。该结果与Keiswetter[18]在3个不同场地进行现场试验得出的结论相似。
2 锤击地震波影响因素的数值模拟
2.1 模型介绍及参数设置
由于现场锤击试验受到场地、参数设置及实验次数的限定,锤击质量及锤击速度只能在较小范围内变化。而本文是通过比较主频、频带宽度及最大振幅的相对值来分析锤击震源对地震波的影响规律,因此基于数值模型来放大重锤及垫板并不影响分析结果。另外,数值模拟还能够分析地层模型各个区域的应力波变化,进而得到锤击震源的激发对整个地层的影响过程。
利用离散元模拟软件,建立锤击震源激发地震波的地层模型,x轴长度为20m、y轴长度为4m、z轴长度为20m。建模时将大锤进行放大,建立一个x轴长度为2m、y轴长度为1m、z轴长度为2m长方体作为大锤模型。同时,将垫板尺寸放大,建立1个x轴长度为2m、y轴长度为2m、z轴长度为0.1m的垫板模型。在模型建成后,对模型进行剖分,剖分的网格单元尺寸为1m。地层模型的底面和侧面设置为黏性边界(即无反射边界)。地层模型顶面由于受到荷载的作用,需反映其力学特征,故将顶面设置为自由面。地层模型内部设置一个Z方向的速度监测点,且正对大锤中心位置。根据上述条件,建成的数值计算模型如图4所示。

图4 数值计算模型图Fig.4 The diagram of numerical calculation model
本节在讨论地层介质时采用的本构模型为Mohr-Coulomb力学模型。
初始的物理力学参数选取分2种:(1)地层:密度为2600kg/m3,体积模量为6.0×109Pa,切变模量为3.6×109Pa,粘聚力为2.0×106Pa,内摩擦角为48°,抗拉强度为2.0×105Pa;(2)大锤及垫板:密度为7600kg/m3,体积模量为1.2×1011Pa,切变模量为7.0×1010Pa,粘聚力为5.0×107Pa,内摩擦角为60°,抗拉强度为5.0×107Pa。
将大锤模型与垫板模型接触面、垫板模型与地层模型接触面看做结构面,接触面力学参数选取分为2种:(1)大锤模型与垫板模型接触面:法向刚度为8.0×1010Pa/m,切向刚度为4.0×1010Pa/m,粘聚力、内摩擦角以及抗拉强度均为0;(2)垫板模型与地层模型接触面:法向刚度为4.0×1010Pa/m,切向刚度为2.0×1010Pa/m,内摩擦角为35°,粘聚力及抗拉强度均为0。
图5为大锤模块与垫板模块、地层模型从接触瞬间开始1.0、5.0、7.0ms中的地表Z向速度云图,由图可知地表Z向速度传至y轴边界需要7ms。地表上各点Z方向上的速度有正有负、形成一条随时间上下振动的应力波。

图5 地表Z向速度云图Fig.5 The Z-velocity contour of land surface
由于现场试验结论认为垫板规格对地震子波频谱分析结果影响并不大,故数值试验只针对大锤质量及瞬时锤击速度两个参数展开分析。
2.2 数值模拟结果分析
2.2.1 大锤质量对地震波传播的影响
通过数值试验研究大锤质量对激发地震波的影响与现场锤击试验研究的参数设置区别在于:现场锤击试验中随着大锤质量变化,其形状大小发生改变。而数值试验在不改变大锤形状大小的情况下,通过改变大锤的密度以达到增大质量的目的。以锤1质量为基准,设置4种不同密度(7600kg/cm3、15200kg/cm3、22800kg/cm3、30400kg/cm3)研究大锤质量增加到基准质量的1~4 倍时对主频、频带宽度及最大振幅的影响,如图6所示。

图6 不同大锤质量比对地震子波的影响Fig.6 Influences of different mass ratio of hammer on seismic wavelet
由图6 (a)可见,随着大锤质量比的增加,数值模拟的结果中,地震波主频基本呈线性下降趋势,大锤质量比由1增至4,地震波主频下降了7.58Hz,总降幅约为52.60%。质量比由1增至4,降幅百分比相比前者分别为15.4%、27.2%和22.99%,说明主频降幅速率随大锤质量比增加呈先增大后减小趋势。而地震波主频的频带宽度在该区间也呈下降趋势:大锤质量比由1增至4,地震波主频的频带宽度下降了5.46Hz,降幅约为49.60%;降幅百分比相比前者分别为9.27%、9.3%和38.8%,说明频带宽度降幅速率随大锤质量比增加呈稳定后急速增大趋势。由图6 (b)可知,最大振幅的变化与前述二者相反,在锤击质量的变化区间内,地震波的最大振幅上升了0.0052dB,涨幅为403.08%。可见最大振幅与主频、频带宽度相比,随锤击质量增大,变化程度更大。
对比以大锤质量为研究变量的现场试验分析结果和数值模拟试验结果,均能发现主频与频带宽度会随大锤质量增加呈二阶非线性减小的规律,最大振幅与大锤质量呈线性相关的关系。
2.2.2 锤击速度对地震波传播的影响
锤击垫板的瞬时速度对激发地震波的影响通过设置4组对照的数值试验进行分析。以第一组瞬时锤击速度2.38m/s为基准,设置大锤模块与垫板之间的距离分别为0.41m、1.65m、3.71m、6.59m,控制锤击垫板的速度分别为2.38m/s、5.69m/s、8.57m/s、11.37m/s,4组瞬时锤击速度与第一组瞬时锤击速度之比分别为1、2.39、3.6、4.77,分析其对主频、频带宽度及最大振幅的影响,如图7所示。

图7 不同瞬时锤击速度比对地震子波的影响Fig.7 Influences of different velocity ratio of hammer striking on seismic wavelet
由图7(a)可知,锤击垫板瞬时速度比从1增至4.77倍时,激发地震波的主频保持在14.49Hz没有发生改变;频带宽度由9.7Hz增加到13.00Hz,增幅为34.02%,频带宽度的增幅百分比相比前者分别为17.01%、7.8%和6.2%,说明频带宽度增幅速率随瞬时速度比增加趋于减小。由图7(b)可见,最大振幅由0.0048增至0.0062,增幅为29.16%。由此可见,在数值模拟中,锤击垫板瞬时速度对激发地震波主频大小没有影响。该参数的改变会影响激发地震波的频带宽度、最大振幅,且锤击速度与这两个地震波频谱特征呈正相关。
对比现场锤击试验分析结果和数值模拟结果发现,除了频带宽度变化稍有不同,其它频谱特征基本一致,瞬时锤击速度的变化对主频产生的影响很小,仅对最大振幅有较大影响。
由于进行数值模拟有对时步进行调节、将局部模型放大,一定程度上会影响数值模拟结果的精度。今后的数值模拟研究可以对试验模型进行改进,使得模型更加贴合实际情况,进一步提高相关研究的精度,更为准确地分析震源参数和地震波传播特征的关系。
3 结论及讨论
(1)对黏性土地表进行锤击,当大锤质量由5kg增至30kg时,主频总降幅为21.43%,频带宽度总降幅为71.39%,最大振幅总增幅为479.6%。随单位大锤质量增加,主频降幅百分比趋于减小,频带宽度降幅百分比先逐渐减小后增大。当瞬时锤击速度由3.13m/s增至5.42m/s时,主频总增幅为4.60%,最大振幅总增幅为79.58%,频带宽度基本不变。锤击垫板的规格对子波的主频、频带宽度及最大振幅基本不产生影响。
(2)通过离散元数值模拟试验发现,当大锤质量由1倍增加至4倍时,主频总降幅约为52.60%,频带宽度总降幅约为49.60%。主频降幅速率随大锤质量比增加呈先增大后减小,频带宽度降幅速率随大锤质量比增加呈先稳定后急速增大趋势,最大振幅总增幅为403.08%。锤击垫板瞬时速度比从1增至4.77倍时,对主频基本没有影响,频带宽度总增幅为34.02%,频带宽度增幅速率随瞬时速度比增加趋于减小;最大振幅总增幅为29.16%。
(3)数值试验结果与锤击试验结果的匹配性较好,在大锤质量和锤击垫板瞬时速度这两个参数设置方面能得出相似结论:主频与频带宽度会随大锤质量增加呈二阶非线性减小规律,而最大振幅与大锤质量呈线性正相关。瞬时锤击速度的变化对主频产生的影响很小,仅对最大振幅有较大影响。

