对电梯群组调用过程的计算机模拟

杨先远

（中山大学药学院，广东广州 510275）

0 引言

电梯需要进行检验和维修以确保其处于安全状态。对电梯设备进行维修保养，一般是对电梯的运转过程进行监控，并对主要工作部件进行定期检查与调试。如发现电梯存在安全隐患，再采取相应的措施处理，防止产生电梯安全事故[1]。目前电梯的维修保养分为半月、季度、半年、年度维修保养[2]。

然而这种维修规则缺乏预见性，因为电梯的使用频率不同，其折旧速率有快有慢，因而其检验周期也不同。目前对电梯维修保养的研究主要针对的是电梯出现的具体问题及解决方法，鲜有涉及电梯折旧率的预测。一般来说，一个机械的工作量越大，其零部件的磨损越严重。电梯的使用量除了与其所属大楼的使用需求呈正相关外，还可能受到其他因素的影响。本文先对居民楼内电梯群组的运行情况进行一定的简化，然后对居民的出行和电梯的调用采用随机抽样的方法进行计算机模拟。考虑不同的电梯调用规则、不同的电梯配备数目以及早晚高峰的影响，计算得到了电梯的调用次数和运行距离。该模拟方法可为制定合理的维修周期提供技术支撑。

1 电梯运行条件的设定

1.1 电梯运行规则

（2）如果两部或以上的电梯距离使用请求所在楼层距离相同，则分为两种模式：①优先模式，调用这几部距离相同的电梯中编号最小的那一部；②随机模式，在这几部距离最近的电梯中随机调用一部。

1.2 居民的出行方式

（1）考虑到居民楼对于电梯使用的需求主要为早晨外出上班、晚上下班回家，故认为每天电梯使用具有早、晚2 个高峰期。概化为0—12 时、12—24 时2 个时段。

（2）忽略居民楼内各层住户之间的来往。即只考虑第2 层到顶层的住户从其所住楼层下行至1 层，以及从1 层返回其所住楼层这两种电梯使用请求。

（3）由于每个人每天需要外出的次数不同，设置一个出行系数来反映楼内所有人每天平均的外出次数。

1.3 电梯的运行过程

忽略电梯的运行时间。即认为在使用请求发出后，电梯立即响应并且瞬时完成该请求，将乘客送至其目标楼层。

1.4 多人同乘一部电梯

多人同乘一部电梯时，会减少电梯的使用次数。采用对总人数乘以一个同乘系数的方式来反映这一影响。

2 编制软件

采用C 语言编程，计算电梯的调用次数和经过的楼层数，以此作为电梯使用率的评价指标。

程序运行需要的输入数据：电梯部数，楼层数，平均每层每天的出行人数，出行系数（一般大于1），同乘系数（一般小于1），电梯运行模式（1——优先模式，2——随机模式），电梯运行模拟的时间（天数）。程序运行过程见图1。

这一时期，风景园林的各项行业法规及政策极大地促进了产业快速良性发展，并且扩大了行业覆盖范围，丰富了风景园林行业内涵。

3 模拟结果

3.1 计算参数取值

（1）研究对象选定为居民楼，地面以上共有30 层。不考虑地下车库。

（2）模拟10 年（3650 d）的使用情况。

（3）楼内居民900 人，考虑出行系数1.39，同乘系数0.56，每日总共需要调用电梯次数上下各为700 次。

3.2 模拟过程中考虑的影响因素

（1）电梯的运行规则。分为优先模式和随机模式两种。

（2）早晚高峰外出与返回的客流比。早高峰分别按照外出人员∶返回人员=9∶1、8∶2、7∶3、6∶4、5∶5 计算，晚高峰出入人员比例与之相反。

（3）配备的电梯数。分别考虑配备3、5、7 部电梯。对电梯编号电梯1、电梯2……电梯7。

3.3 群组运行规则对电梯使用量的影响

配备5 部电梯，早高峰出入客流比为8∶2，晚高峰为2∶8。经计算，得到每部电梯的调用次数（图2），经过的楼层数（图3）

3.4 早晚高峰期间外出与返回的客流比对电梯使用量的影响

配备5 部电梯，考虑客流比分别为1∶9、2∶8、3∶7、4∶6 及5∶5。优先模式下的模拟结果见图4、图5，随机模式下的模拟结果见图6、图7。

图1 程序框图

图2 两种运行规则下每部电梯的调用次数

3.5 配备的电梯数对电梯使用量的影响

采用早高峰出入客流比为8∶2，晚高峰出入客流比为2∶8。计算在配备3 部、5 部及7 部电梯时的使用量。优先模式下的模拟结果见图8、图9，随机模式下的模拟结果见图10、图11。

4 模拟结果分析

根据图2、图3 可知，电梯运行规则对于电梯的使用量具有显著影响。

在优先模式下，每部电梯的调用次数和经过楼层数均随着电梯编号的增大而减少，并且电梯1（被优先调用的电梯）的调用次数和经过楼层数都是电梯2 的3 倍多。这说明，电梯1 的折旧速率将高于其他电梯，应具有较短的维修周期。

图3 两种运行规则下每部电梯经过的楼层数

图4 优先模式下每部电梯的调用次数（配备5 部电梯）

图5 优先模式下每部电梯经过的楼层数（配备5 部电梯）

在随机模式下，各部电梯相应的调用次数和经过楼层数相差不大。这表明各部电梯之间的折旧率相近，可采用相同的维修周期。

根据图4～7 的数据，可以发现出入客流比对于电梯的使用量也具有重要影响。

在优先模式下（图4、图5），对某一固定的客流比，各电梯的调用次数和经过的楼层数都随着电梯编号的增大而减少。随着客流比趋近于5∶5，各个电梯之间使用量的差异逐渐缩小。这意味着，对于执行优先模式的电梯群组而言，出入客流比越平均，几部电梯之间的使用量越接近，相应的维修周期也更接近。

在随机模式下（图6、图7），对于每一个确定的出入客流比，各电梯的调用次数和经过楼层数大致相同。随着出入客流比趋近于5∶5，每部电梯的调用次数没有出现明显变化，而每部电梯经过的楼层数都随之下降。这说明处于随机模式下的各部电梯具有相似的折旧率。

图6 随机模式下每部电梯的调用次数（配备5 部电梯）

图7 随机模式下每部电梯经过的楼层数（配备5 部电梯）

图8 优先模式下每部电梯的调用次数

图9 优先模式下每部电梯经过的楼层数

图10 随机模式下每部电梯的调用次数

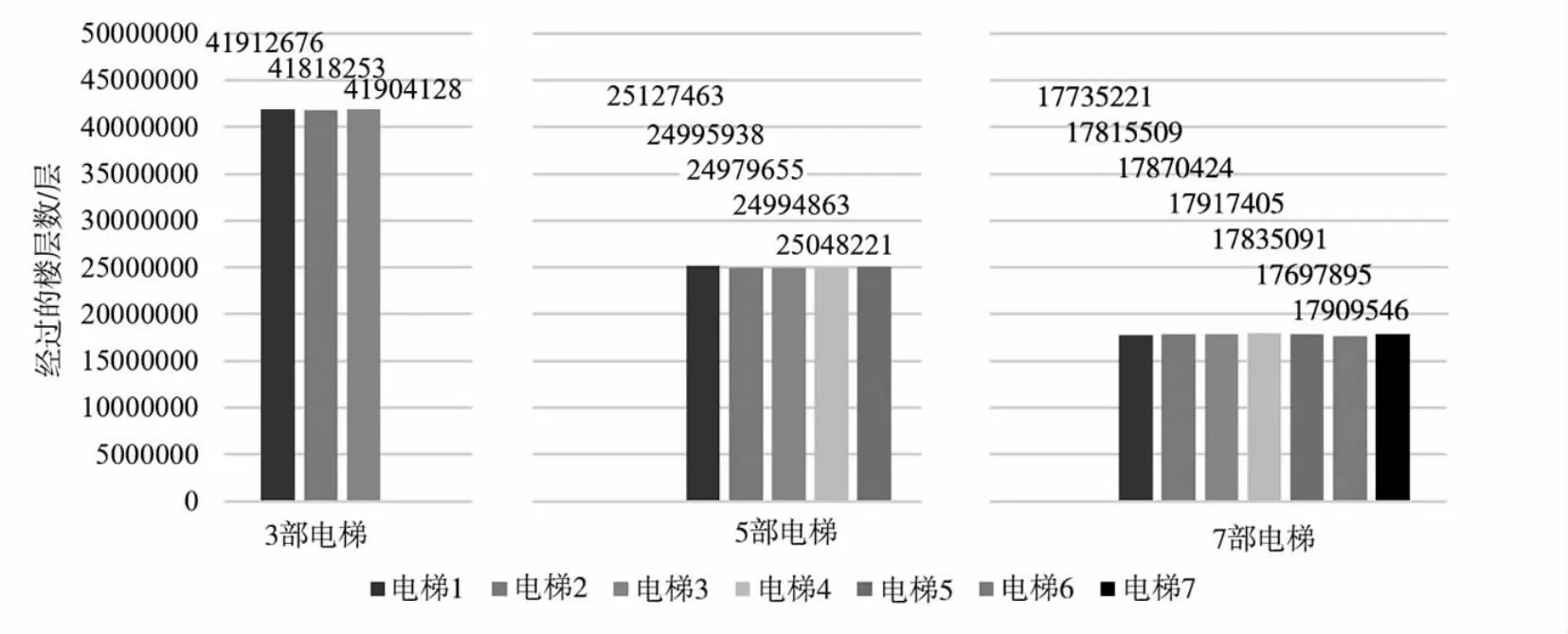
图11 随机模式下每部电梯经过的楼层数

此外，无论采用哪种运行规则，5 部电梯经过的楼层数的总和都随着出入客流比接近于5∶5 而减少，这在一定程度上可以延缓电梯群组的折旧。造成该现象的原因可能是：①在出入客流比悬殊的情况下，电梯总是更多地运送单方向流动的乘客，因此电梯在1 楼与乘客所住楼层之间往返时，空梯运行的距离在总运行距离中占比较高；②在出入客流比接近于5∶5 时，电梯的利用率相对较高，即空梯运行的距离在总运行距离中占比低。因此在运行总次数不变的情况下，出入客流比越趋近于5∶5，电梯经过的楼层总数就越低。

根据图8、图9 的结果，可以看出在优先模式下，无论配备几部电梯，每部电梯的调用次数和经过楼层数均随着电梯编号的增大而减少，但是电梯1（被优先调用的电梯）的调用次数和经过楼层数始终是电梯2 的3 倍左右。此外，增加配备的电梯数目，虽然可以让电梯1 的使用量和电梯群组经过的楼层数的总和下降，但降幅不明显。这反映出电梯配备的数目对于应用优先模式的电梯群组产生的影响较小，因此不能通过增加电梯数目来延缓电梯的折旧。

根据图10、图11 的结果可知，在随机模式下，当配备一定的电梯数目时，每部电梯的运行次数和经过的楼层数基本一致。随着电梯配备数目的增加，各电梯的调用次数和经过楼层数都逐渐减少，且降幅相对比较显著，电梯群组经过楼层数的总和也略有下降。这是由于在随机模式下，新增加的设备可以有效地分摊需求的总量，从而降低了每个设备的使用量，延缓了电梯的折旧。但是，增加电梯的数目也会提高电梯的安装成本，因此用增配电梯的方式延缓电梯折旧的方法性价比不一定高。

5 结语

本文考虑电梯的调用规则、出入客流比及电梯数目3 个因素，模拟了电梯的运行过程。通过计算，得到以下结论：

（1）电梯群组的运行规则对于电梯群组折旧快慢产生的影响最大。优先模式下，被优先调用的电梯工作量最大，折旧率最高，因此其维修周期应该最短；随机模式下各部电梯之间工作量相近，因而可采用相同的折旧率和维修周期。

（2）出入客流比也会影响电梯群组的使用量。出入客流比越接近于5:5，电梯群组的运行总距离越短，即电梯群组的总使用量越小，使得电梯群组的折旧速率更低。即均匀的出入客流比对应较低的折旧率。

（3）配备不同数目的电梯会对每部电梯的工作量产生影响。虽然增加电梯数目可以延缓每部电梯的折旧，但这也同时增加了电梯购置的成本。

由于本文模拟计算中没有考虑电梯运行的时间，没有涵盖像办公楼那样存在层与层之间往来的情况，也没有设计更多的运行规则，这些都是下一步需要研究的内容。