延迟焦化开工线腐蚀机理及温度模型预测
任 佳, 王西刚, 赵梦恩, 金浩哲
(浙江理工大学 机械与自动控制学院,浙江 杭州 310018)
随着现代工业的发展,轻质油的需求量日益增加,石油资源短缺的问题日渐突出。延迟焦化是一种常用的原油二次加工工艺,可以以炼油厂渣油、劣质渣油等重质低价油作为原料,通过热裂化和缩合反应生产轻质油[1]。但随着焦化装置的腐蚀环境不断恶化,受流动、传热、相变等腐蚀机理复杂多变的影响,设备、管线的腐蚀已经成为影响焦化装置安全平稳长周期运行的主要危害。
延迟焦化装置腐蚀的类型主要有3种:高温硫腐蚀(240 ℃以上)、低温湿H2S腐蚀(120 ℃以下)和烟气露点腐蚀。其中,温度是影响腐蚀类型和腐蚀速率的重要因素,主要原因是温度影响了H2S等活性硫化物与金属的化学反应以及非活性硫化物的分解速率等[2]。杨建炜等[3]分析了温度对管线钢H2S腐蚀行为的作用,结果表明腐蚀程度会随着温度的升高先加强后减弱。田伟等[4]指出温度对80SS油管钢腐蚀行为的影响,所得结论与文献[3]中的实验结果一致。许霖风一等[5]的研究表明,温度和H2S浓度对设备管道腐蚀有关键性的影响。开工线在开工再生产时易形成死区,反应产生的水汽、油气和H2S气体均会滞留在开工线管道顶部无法排除,发生严重的腐蚀作用,引起管线开裂、高温热油泄漏,甚至造成火灾爆炸等重大安全问题,因此需要对可能发生的严重腐蚀情况进行预警并控制影响腐蚀速率的因素来延缓装置的腐蚀,而开工线区域发生的湿H2S腐蚀会受到H2S浓度[6]、pH值[7]、压力[8]和温度[9]等因素的影响。在调研了现场装置中各因素的可控性和对腐蚀的影响程度之后[10],笔者选择开工线温度作为延迟焦化装置腐蚀失效的表征参数,由于直接测量开工线温度成本较高且测量结果存在延迟性,因此考虑通过软测量的方法进行开工线温度预测。高斯过程回归(GPR)[11]是一种化工领域常用的软测量方法,可以给定预测结果的方差,便于对腐蚀风险进行精确评估。但在实际应用中,其性能会受到所选核函数及参数优化方法的限制,准确性和稳定性有待提高。针对此问题,笔者在GPR模型基础上建立了GSA[12]优化的 GSA-CKGPR 模型,有效提高了模型准确性和稳定性。
笔者从延迟焦化装置工艺过程出发,介绍了其工艺关联流程,分析了延迟焦化过程中开工线发生的湿H2S腐蚀机理,并确定了开工线温度作为装置的腐蚀失效表征参量,通过建立的GSA-CKGPR模型,实现开工线温度的准确稳定预测,为装置工艺参数优化操作提供指导。
1 延迟焦化系统工艺分析
1.1 工艺过程关联研究
图1为延迟焦化系统流程图。整套焦化装置为两炉四塔流程(图中仅显示C-101A/B,即一炉两塔),两两一组成对工作,每组每次运转48 h,其中生焦24 h,吹气、注水、注泥等清焦过程24 h,1塔在反应生焦时,另1塔处于除焦阶段。其生产流程为:原料油首先经回流换热器(E-101A-F)换热后进入原料油缓冲罐(D-101),再被原料油泵(P-101A/B)抽出,经换热器(E-105A-F)换热后(301 ℃)与焦化分馏塔底循环油(360 ℃)混合(318 ℃),再依次经过加热炉进料缓冲罐(D-102)、加热炉进料泵(P-102A/B)后进入焦化加热炉(F-101A/B)加热,炉出口温度在485~490 ℃,最后通过四通阀进入焦炭塔(C-101A-D),发生热裂化和缩合反应,产生的油气进入分馏塔,经冷凝分馏后送出装置。
1.2 湿H2S腐蚀机理
重质原料油在塔内反应结焦,当一台塔内的焦炭积聚到一定高度后,就需要切换操作,将塔内焦炭从塔底排出,焦炭塔塔顶的气流则通过油气线进入分馏塔分馏完成循环。开工线一端连通四通阀顶部,一端与焦炭塔塔顶相连,开工再生产时,部分热油物料经四通阀、开工线进入焦炭塔塔顶,在重力作用下热油沿塔壁从上至下流动到塔底,从而对焦化塔进行预热。由于开工线与焦炭塔顶连通,在预热过程结束,开工线顶部阀门关闭后,阀门到连通焦炭塔的一段开工管线就形成了死区,而由于装置给水、溢流等工艺过程产生了水,同时开工线内部温度较低(实际测量得到的最高温约为117 ℃,最低温约为34 ℃),所以易发生低温湿H2S腐蚀,排除了发生另外2种腐蚀失效的风险。
低温湿H2S的腐蚀可以通过如下反应[13]描述:
阳极反应为:
Fe→Fe2++2e-
(1)
电离反应为:
H2S→HS-+H+
(2)
HS-→H++S2-
(3)
阴极反应为:
H++e-→H
(4)
2H→H2(gas)
(5)
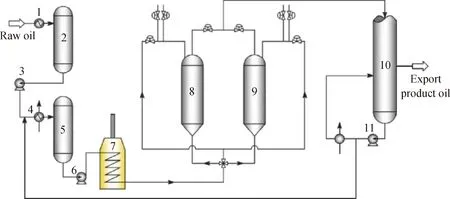
图1 延迟焦化系统流程图Fig.1 Flowchart of the delayed coking system1—Heat exchangers E-101 A-F; 2—Feed buffer tank D-101; 3—Feed pumps P-101 A/B; 4—Heat exchangers E-105A-F;5—Furnace feed tanks D-102; 6—Furnace feed pumps P-102A/B; 7—Furnaces F-101 A/B; 8—Coke drum C-101A;9—Coke drum C-102A; 10—Fractionator T-101; 11—Recycle oil pumps P-103A/B
腐蚀反应为:
Fe2++S2-→FeS
(6)
图2为湿H2S腐蚀开裂机理图。在反应发生的初期,腐蚀反应形成由FeS等Fe-S化合物组成的产物膜,随着产物膜的厚度增加,能够起到一定的耐腐蚀作用[14];但随着反应的不断进行,保护膜会在H2S溶液的作用下遭到破坏,从而使得腐蚀反应继续进行[15],进一步对材料造成腐蚀。
在上述反应过程中,由于H2S及其电离产生的HS-的毒化作用,阴极反应中氢原子转化为氢气的反应过程(式(5))会受到抑制[16],部分氢原子会扩散到管道材料内部,随着氢原子的增加而形成氢压,使得材料脆化,在应力作用下产生氢脆开裂等问题[17]。
在腐蚀过程中,温度的影响形式复杂多变,且在其中有着关键的作用:首先,温度影响着H2S等气体在溶液中的溶解度,直接影响着腐蚀和毒化作用的程度;其次,温度本身对腐蚀电化学反应的进程和速率也有着较大的影响;最后,温度也会对水的形态、腐蚀产物的成膜机制等产生影响[18],因此,温度对于装置的腐蚀风险评估和预警具有较高的价值,同时温度易于控制,变化范围广泛,相比于其他腐蚀影响因素,具有更多的可调控空间。所以选择温度作为装置腐蚀失效的表征参数。

图2 湿H2S腐蚀开裂机理图Fig.2 Wet hydrogen sulfide corrosion cracking mechanism
2 开工线温度预测模型构建
2.1 数据样本采集及处理
在对延迟焦化装置现场考察的同时,结合工程经验,对油气线温度、溢流线温度、开工线压力、塔内温度、塔入口温度和开工线温度进行了采集。考虑到GPR模型在非线性以及高维数据上表现较好的特性,在特征筛选过程中保留了所有特征,模型的输入和输出数据信息如表1所示。
由于现场采集到的数据具有较高的噪声,为了减弱异常值和极端值对模型的影响,笔者对数据进行了标准化处理。假设表1中某个待处理的变量为s(可以是表1中的任一变量),其标准化之后的值s*可通过下式计算得到,其中μ是该变量的样本均值,σ是样本标准差。
s*=(s-μ)/σ
(7)

表1 焦化系统输入输出物理量名称Table 1 Data information of coking system
2.2 模型构建
GPR模型通过核函数构建待测变量联合正态分布的协方差矩阵,并基于训练数据优化核函数,得到最大后验概率模型。模型构建的关键是核函数选择以及超参数优化,基于训练数据构建了Matern核(KM)和平方指数核(KSE)的复合核函数(KCK),如式(8)~(10)所示。式(10)中包含的4个参数M、SE、ωM和ωSE,即为模型需要优化的超参数。使用GSA进行超参数的优化,解决了传统共轭梯度法在优化过程中存在对初值依赖性强和容易陷入局部最优的问题。算法步骤如图3所示。
(8)
(9)
KCK(x,x′)=ωMKM(x,x′)+ωSEKSE(x,x′)
(10)
图3流程中GSA的模型参数粒子初始种群数为20,模型参数粒子速度和位置更新公式分别为式(11)和式(12)。笔者使用模型预测结果的均方根误差(式(13))作为对应模型参数的适应度值。
v(t+1)=r×v(t)+a(t)
(11)
x(t+1)=x(t)+v(t+1)
(12)
式(11)~(12)中:v(t)为粒子在t时刻的速度;x(t)为粒子在t时刻的位置;r是取值为[0-1]的随机数;a(t)为粒子在t时刻的加速度,其值与粒子在t时刻受到的作用力、惯性质量和适应度值有关,具体计算流程和GSA的原理可以参考文献[12]。
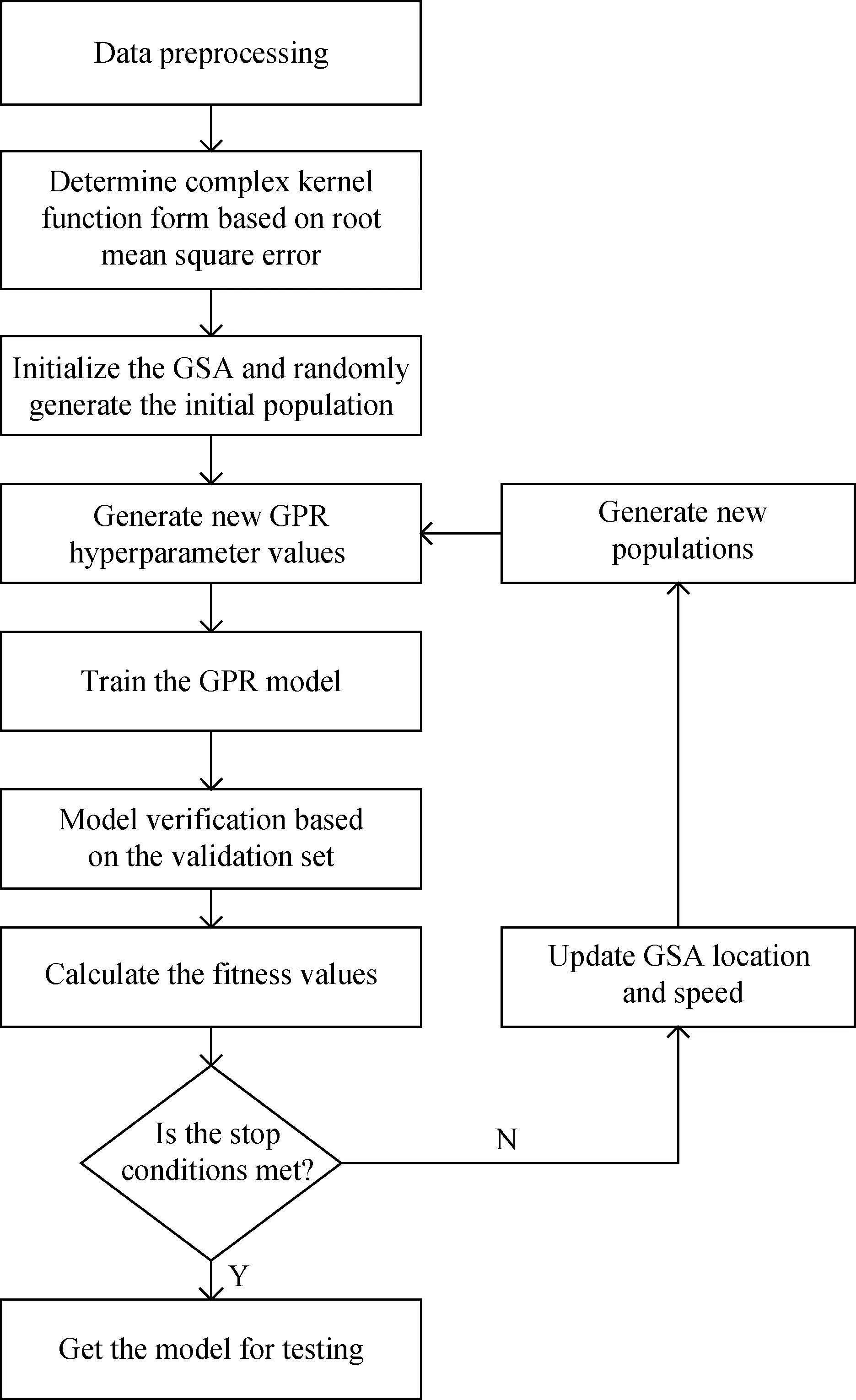
图3 GSA-CKGPR算法流程Fig.3 Flow chart of GSA-CKGPR algorithm
3 开工线温度预测结果与讨论
笔者用从现场采集到的2800组样本进行训练和测试,数据分为3部分,按照采集时间顺序前1500组作为训练集,中间500组作为验证集,最后800组作为测试集。使用均方根误差(RMSE)的2种形式作为评价标准,其计算如式(13)和式(14)所示。RMSE1能够对总体预测结果的准确程度进行度量;而开工线温度变化范围较大,通过RMSE2则能够对整体预测结果相对于真实值的相对误差大小进行评估。
(13)
(14)


由图4和表2可知,GSA-CKGPR模型的RSME1和RMSE2仅分别为4.45 ℃和7.7%,在测试的6个模型的结果中是最小的,其余5个模型预测效果从好到差依次为GSA-GPR、GSA-SVR、PSO-GPR、GA-GPR、GPR。由表2可知:在使用GSA算法优化时,多核GPR模型比SVR模型更加精确;GSA优化方法比PSO和遗传算法(GA)方法预测更准确,更加适用于装置开工线温度数据的优化。
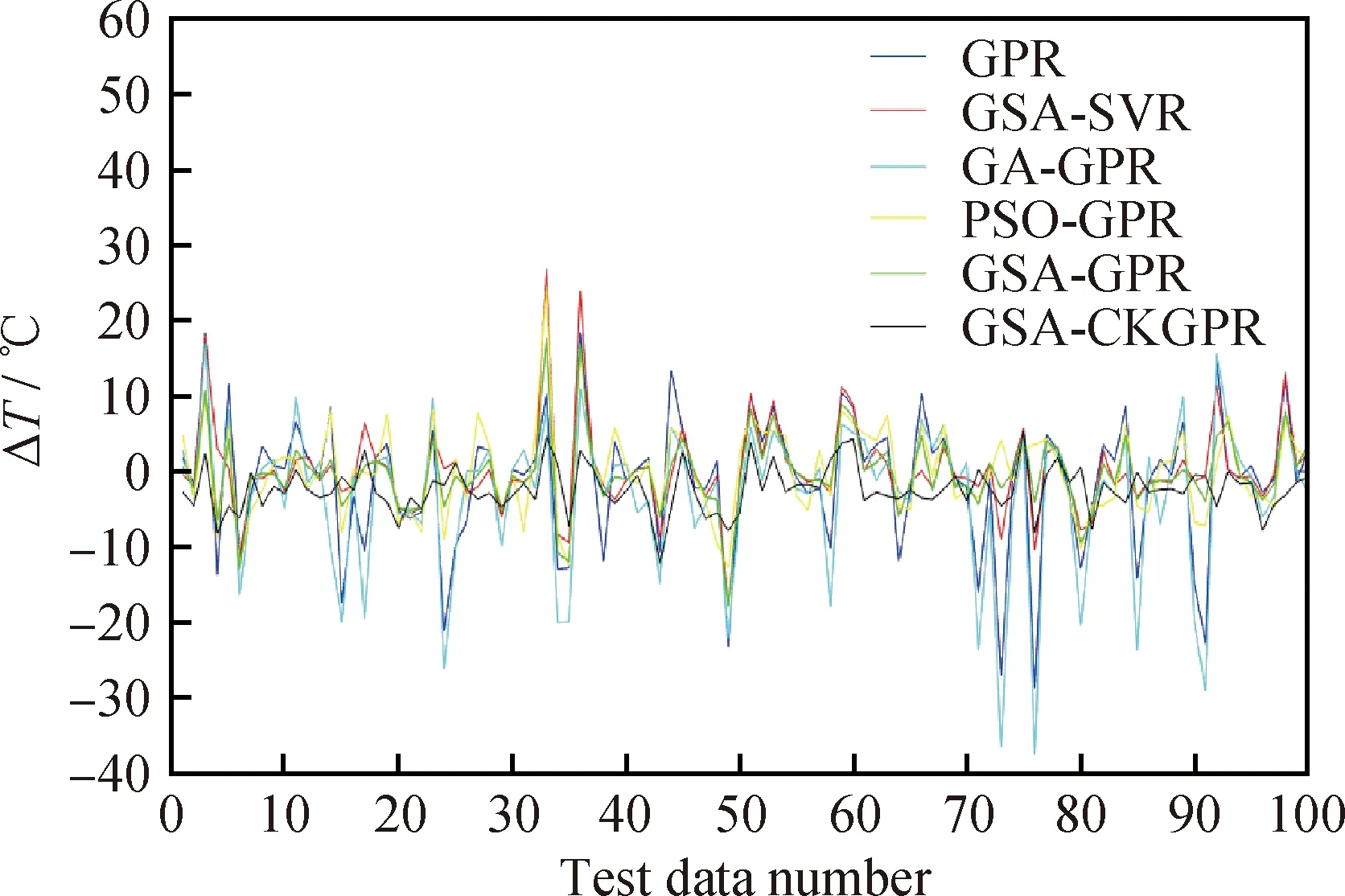
图4 各个模型误差曲线图Fig.4 Error curve of each modelTop 100 samples
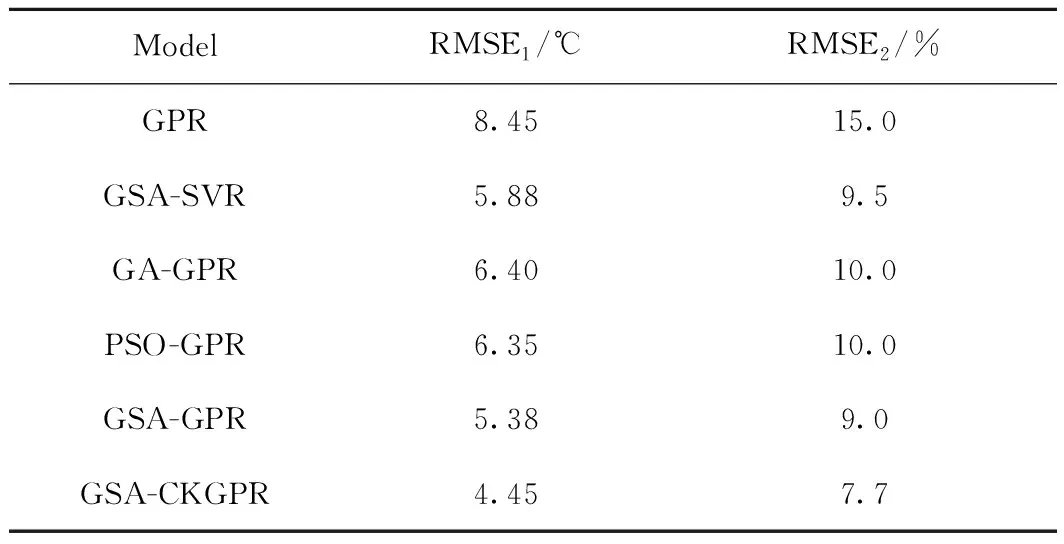
表2 不同模型的RMSE1和RMSE2Table 2 RMSE1 and RMSE2 values of different models
图5为GPR、GSA-GPR和GSA-CKGPR的预测结果及真实数据按照时间顺序排列的曲线图。由图5可知,真实测量数据的变化曲线上(黑色线条,圆形点),编号1~70和80~90样本的温度一直是处于较大幅度的变化中,而编号70~80和90~100样本的温度变化则比较平稳。这种温度变化的不规律性会增加模型预测的难度。相比于GPR模型(绿色线条,十字形点)和GSA-GPR模型(紫色线条,星形点),GSA-CKGPR模型的预测曲线(红色线条,矩形点)与真实测量数据的曲线整体上更加接近,同时也没有误差较大的异常预测点,而GPR模型在编号73、76、89、90和91样本的预测结果(图中红色框内)存在明显的误差,这些点都处在温度变化剧烈与平稳之间的过渡区域,说明了温度变化不规律导致模型性能下降。而GSA-CKGPR和 GSA-GPR 则通过GSA优化方法克服了这种问题,提高了模型的稳定性。
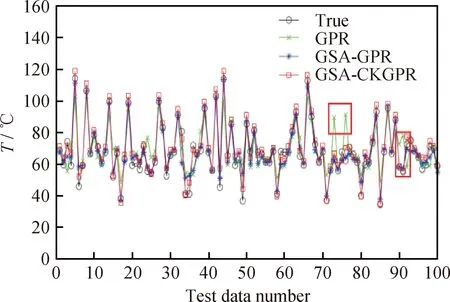
图5 3种模型温度预测结果Fig.5 Temperature prediction results of three different models
为了进一步对模型的稳定性进行量化分析,绘制了图6所示的各个模型预测值-真实值散点分布图,并根据实际的工艺需求在每幅图中添加2条表示稳定边界的辅助线,分布在2条辅助线之间的点越密集,表明该模型的预测结果越稳定,产生异常预测结果的风险也就越小。
由图6中点的分布情况可以大致看出,GSA-GPR、GSA-SVR、GSA-CKGPR模型预测结果在辅助线之间的点较为密集,稳定性较好。在量化分析中,计算了各模型预测结果位于2条辅助线之间的点占总测试点的比例值,分别为56.24%(GPR)、57.23%(PSO-GPR)、67.86%(GA-GPR)、80.10%(GSA-SVR)、80.35%(GSA-GPR)、84.05%(GSA-CKGPR)。结果表明,GSA-CKGPR模型更加稳定。
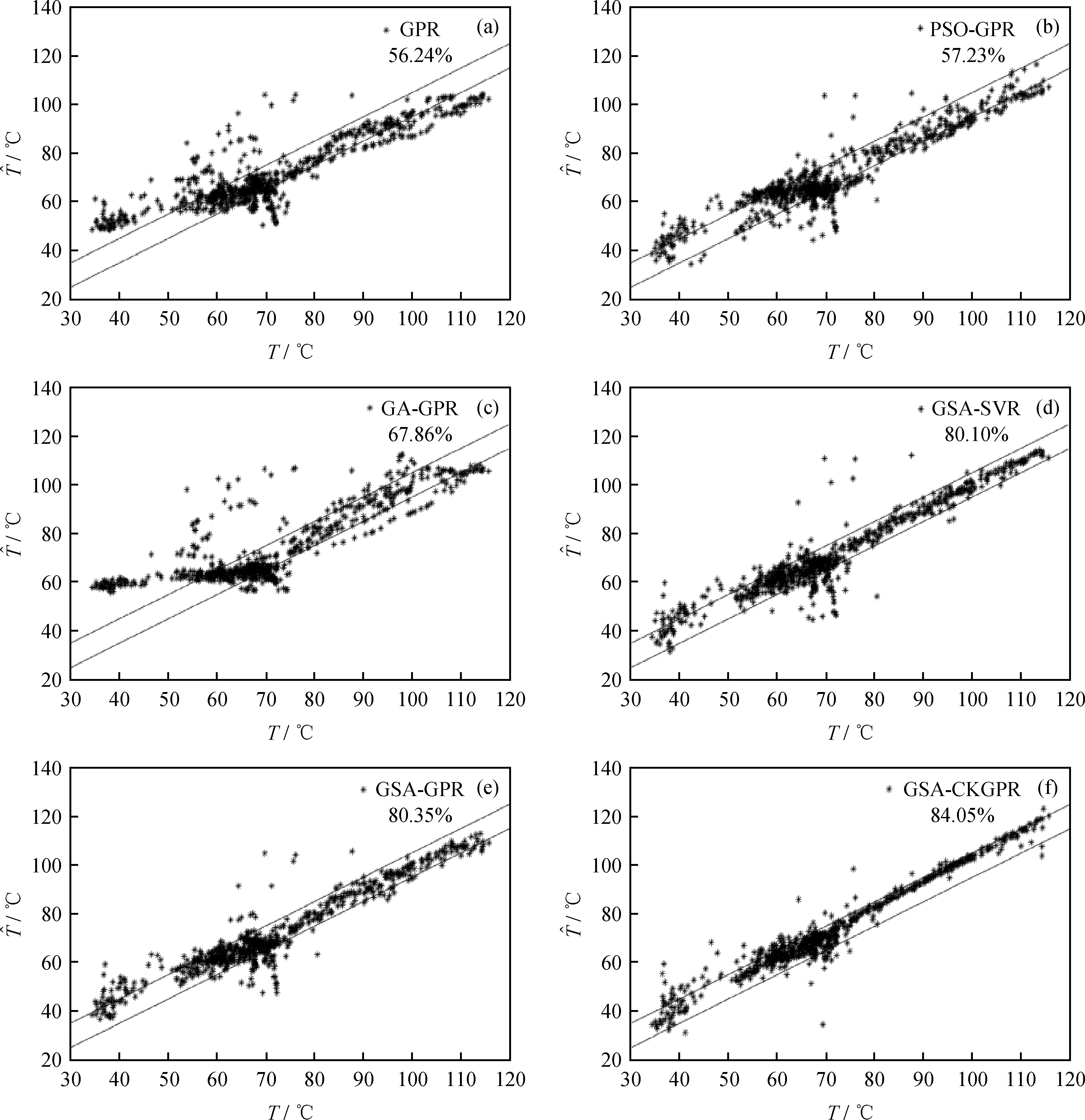
图6 不同模型预测值-真实值对比图Fig.6 Comparison between prediction and real values from different models(a) Prediction values vs. real values of GPR; (b) Prediction values vs. real values of PSO-GPR;(c) Prediction values vs. real values of GA-GPR; (d) Prediction values vs. real values of GSA-SVR;(e) Prediction values vs. real values of GSA-GPR; (f) Prediction values vs. real values of GSA-CKGPR
4 结 论
基于延迟焦化系统工艺关联过程进行研究,确定了装置开工线的低温湿H2S腐蚀机理和腐蚀过程;在此基础上综合考虑了影响腐蚀发生的因素及其对反应的影响形式,明确开工线温度作为腐蚀状态评估的表征参数;最后针对装置开工线温度难以直接准确测量的问题,基于GSA、PSO以及GA 3种优化方法对GPR、SVR 2种基本模型进行优化,并对得到的6个算法模型进行实验对比。结果表明,GSA-CKGPR模型将GPR模型的均方根误差由8.45 ℃降低到4.45 ℃,稳定预测结果由总测试数量的56.24%提高到了84.05%,为延迟焦化装置腐蚀风险评估和预警提供了稳定可靠的数据预测模型。

