海南核电一回路泄漏率的优化算法

李 静，刘 逸

（海南核电有限公司，海南昌江 570105）

0 引言

海南核电一回路泄漏率通过容控箱液位、稳压器液位和一回路平均温度计算获得，现有计算方法能够简单快速得到一回路泄漏率。这种方法也有缺点，计算结果波动大、可靠性不高，选点不同会导致计算结果偏差很大。产生这一现象的原因是计算过程中没有充分利用该时间段内数据。为了解决这个问题，将时间段内的所有数据都用于计算一回路泄漏率。

1 一回路泄漏率改进前的算法

海南核电现有的一回路泄漏率计算方法是记录T0时刻的稳压器液位、容控箱液位和一回路平均温度。然后记录2 h 后的稳压器液位、容控箱液位和一回路平均温度，再通过式（1）计算得到一回路泄漏率Fp。

式中 N1——计算开始时刻的容控箱液位，m

N2——计算结束时刻的容控箱液位，m

N3——计算开始时刻的稳压器液位，m

N4——计算结束时刻的稳压器液位，m

T1——计算开始时刻的一回路平均温度，℃

T2——计算结束时刻的一回路平均温度，℃

Δt——计算开始到计算结束的时间间隔，固定值2 h

这种计算方法的前提条件是容控箱液位、稳压器液位和一回路平均温度为线性变化，或者近似为线性变化。但实际这些数据都不是按照线性变化，而且很多时刻波动较大，导致式（1）计算结果误差较大。

以4 月14 日8：00—10：00 数据为例，说明现有计算方式的问题。容控箱液位2 h 内的变化曲线如图1 所示，通过最小二乘曲线拟合得到的容控箱液位随时间变化的解析表达式：y=0.010 5x-461.99，纵坐标单位m，横坐标单位min。

稳压器液位2 h 内的变化曲线如图2 所示，通过最小二乘曲线拟合得到的稳压器液位随时间变化的解析表达式：y=-0.012 2x+536.82，纵坐标单位m，横坐标单位min。

一回路平均温度2 h 内的变化曲线如图3 所示，通过最小二乘曲线拟合得到的一回路平均温度随时间变化的解析表达式：y=0.480 6x-20 808，纵坐标单位℃，横坐标单位min。

图1 容控箱液位变化曲线

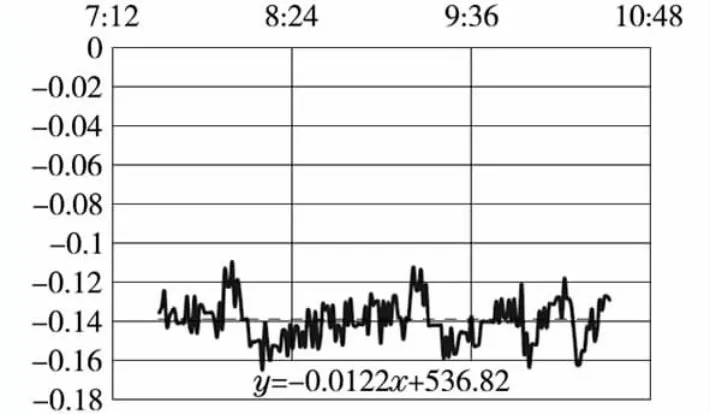
图2 稳压器液位变化曲线

表1 通过PT1RCP010 规程计算得到的一回路泄漏率

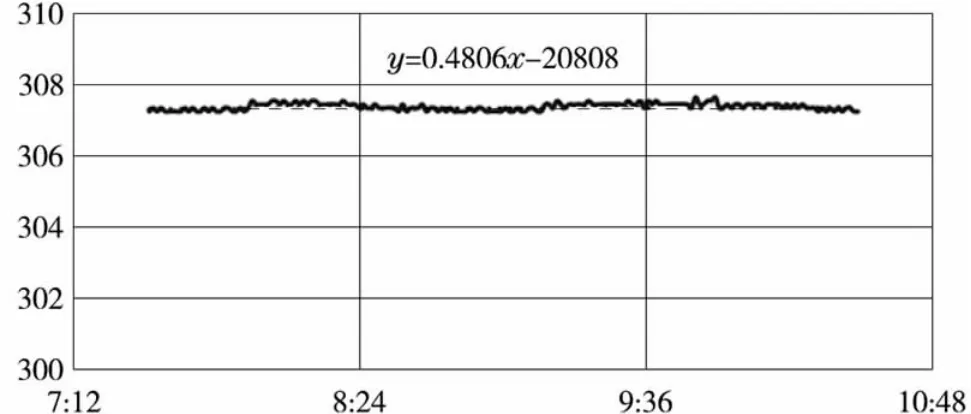
图3 一回路平均温度变化曲线

通过式（1），对7：30—9：3 的泄漏率进行计算，为了说明现有计算方法的问题，分别计算每隔1 min 的一回路泄漏率。表1 的计算结果表明，不同取样点计算结果偏差很大，在10 min 的间隔时间内，最小计算结果6.6 L/h，最大计算结果81 L/h，计算结果方差达到22.68。

2 一回路泄漏率改进后的算法

为了减小计算结果的方差，提高结算结果的稳定性，必须将2 h 内的所有数据都用于计算，采用曲线拟合方法可以解决这个问题。通过一阶曲线拟合得到的容控箱液位解析表达式：y=0.010 5x-461.99，稳压器液位解析表达式：y=-0.012 2x+536.82；一回路平均温度解析表达式：y=0.480 6x-20 808。

通过曲线拟合方法获得的相同初始时刻的一回路泄漏率，T0和T1时刻与表1 一致，泄漏率计算结果为6.182 4 L/h、6.410 6 L/h、7.307 6 L/h、7.902 3 L/h、8.428 9 L/h、8.885 9 L/h、9.097 5 L/h、9.316 0 L/h、9.811 8 L/h、10.751 L/h。计算结果的方差仅为1.468。通过对比可知，使用曲线拟合方法计算结果稳定性大幅提高。

3 结论

海南核电现有的一回路泄漏率计算方法具有较大的不稳定性，为提高计算结果的稳定性，本文将原有的两点式计算方式改为曲线拟合计算方式。通过对比计算，可靠性大幅提高，计算结果的方差由22.68 下降到1.468。本方法不仅适用于海南核电，还适用于其他M310 机组。