基于神经网络的金刚石色心自动识别算法实现

郑子贤, 张小涵, 陈 冰, 徐南阳

(合肥工业大学 电子科学与应用物理学院,安徽 合肥 230601)

0 引 言

金刚石的主要化学成分是碳,同时包含氮、硅、硼等杂质,杂质的渗入以及多种结构缺陷使得金刚石呈现不同颜色。由于氮原子和碳原子的大小最为接近,容易进入晶格,因此天然金刚石中掺杂浓度最高的一般是氮元素。金刚石氮-空位(nitrogen-vacancy,NV)色心就是金刚石中由氮原子形成的晶体缺陷,在金刚石中,若1个碳原子被1个氮原子替代并且相邻位置的碳原子缺失形成空穴,则构成1个NV色心。金刚石NV色心具有荧光稳定性好、荧光强度高,其中的电子自旋相干时间较长,同时易于实现微波操控和光学激发等优良特性,这使得金刚石NV色心被广泛应用于量子技术领域。

本文实验采用的系统结构如图1所示。在真实的实验场景下,扫描到的数据是金刚石某区域的单光子计数率矩阵,本文把计数率矩阵转化为灰度图。由于实验中不可避免地存在噪音和干扰,色心图中会存在由这些干扰产生的亮斑,加大了NV色心识别的难度;目前的目标检测模型对于大目标检测的效果比小目标要好,而对于NV色心图,大部分NV色心目标相对于图片尺度都是比较小的目标,同样不利于色心目标的检测。目前的实验平台识别NV色心主要依赖于实验人员以往的经验,再借助光探测磁共振(optically detected magnetic resonance,ODMR)实验来确认是否为NV色心,存在识别速度慢、误识别率高等问题。

图1 系统结构图

近年来,卷积神经网络被广泛应用在图像相关领域[1-4]。目前基于卷积网络的目标检测方法主要有2类:① 基于候选框提取的两阶段(two stages)算法,主要由文献[5]的基于区域的卷积神经网络(region-based convolutional neural network, R-CNN)模型发展而来,包括进一步改进的空间金字塔池化网络(spatial pyramid pooling in deep convolutional networks for visual recognition, SPP-Net)[6]、Fast R-CNN[7]、Faster R-CNN[8]等模型,这些模型网络相对复杂、运行速度慢,但是网络精度高;② 直接回归的一阶段(one stage)目标检测算法,主要是YOLO[9]及其改进的模型,以及SSD(single shot multiBox detector)模型[10],和两阶段算法相比,一阶段算法模型结构简单、容易训练,在获得检测速度提升的情况下依然能够保持比较高的识别率。

本文在以上目标识别方法的基础上,针对金刚石NV色心图噪音大、色心目标较小的特点,提出金刚石NV色心自动识别框架,可以快速、准确地对色心目标进行自动识别,大大提高了实验效率。

1 算法框架

1.1 基础网络设计

本文采用的基础网络结构见表1所列。表1中Conv×2表示完全一样的卷积层堆叠2次。网络在AlexNet[11]和VGGNet[12-13]的基础上作出改进。整个网络包含8个阶段(又称block)的特征提取过程,8个block逐层堆叠形成整个特征提取网络,即每个block的第1层卷积层的输入是前一个block最终的输出,当前block最后一层的输出为下一个block的输入。每个阶段会输出相应的特征提取结果,由于金刚石NV色心图被缩放至300×300大小作为网络的输入,经过每个阶段的特征提取后,特征图尺度分别为150×150、75×75、38×38、19×19、10×10、5×5、3×3、1×1。

表1 基础网络结构

注:填充取值为1表示在输入特征图周围填充1个像素点的值,取值为0表示不作填充。

对于block设计,本文采用的卷积核有2种尺度,即1×1和3×3。与更大尺度的卷积核相比,如5×5、7×7,在相同感受野的情况下,3×3卷积核具有更少的网络参数以及更多的非线性表达。网络参数更少意味着模型更容易训练并且降低了过拟合的风险,更多的非线性表达则提高了模型的表达能力。

此外,使用1×1卷积核可以大大降低模型运算量,如图2所示。图2中,W、H、C分别表示特征图的宽度、高度、通道数,w、h分别表示滤波器的宽度、高度。图2a所示为没有使用1×1卷积核的2层网络,图2b所示为使用了1×1卷积核的2层网络。图2a网络和图2b网络的输入、输出完全一致,但不同的是,图2a网络乘法运算量为W2H2C2whC1,图2b网络乘法运算量为W1H1C12+W2H2C2whC12。

在图2b网络乘法运算量中,通常后项远大于前项,因此,图2b网络与图2a网络的运算量比值为:

在基础网络设计中,本文通过控制C12=0.5C1,大大降低了模型运算量。

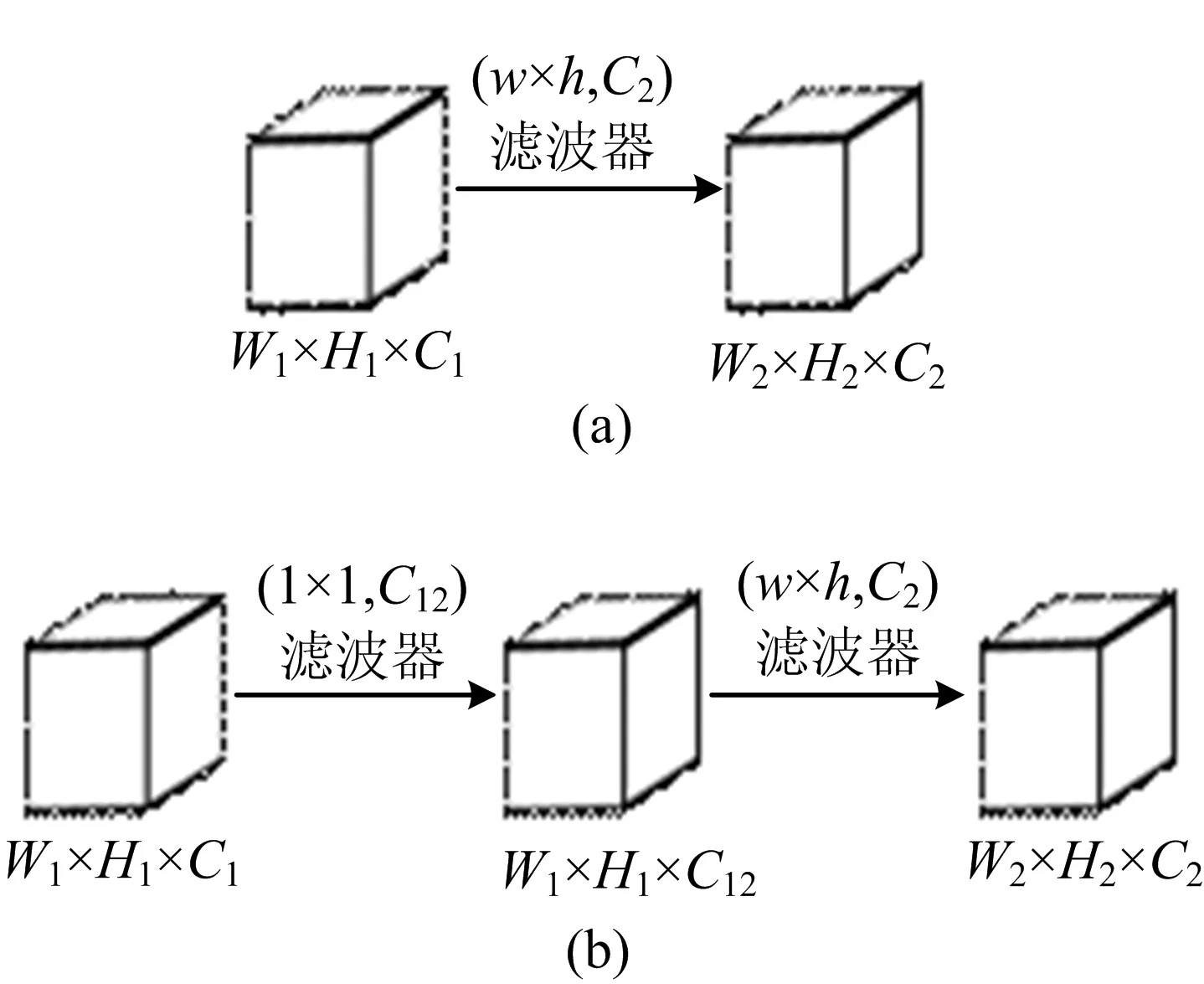
图2 通道降维

1.2 多尺度检测

金刚石NV色心目标比较小,对于1.1节中的特征提取网络,本文除了在最终的特征图上预测目标位置和类别概率,还采用多尺度检测的思路以提高模型对色心目标的检出能力,如图3所示。图3a所示为仅使用最终输出的特征图预测,此时的特征图语义信息丰富,但是特征图尺度小,会丢失大量的位置信息,不利于预测金刚石NV色心的位置。而在图3b中,模型在多个尺度的输出特征图上进行预测,和高层的特征图相比,浅层的特征图会更多地包含色心目标的位置信息,这会提高模型对金刚石NV色心位置的预测能力。本文在block4、block5、block6、block7、block8等5个尺度的特征图上进行预测。

图3 多尺度检测

本文在模型中引入了先验框的概念,即在block4～block8模块的输出特征图上,每个特征点对应9种不同的先验框(包含了3种尺度和3种比例)。模型预测的是每个先验框区域的二分类概率分布和对先验框位置参数x、y、w、h的修正。其中,x、y为边框中心点坐标;w、h分别为边框的宽和高。因此,每个特征点对应的输出通道数为9×(2+4)=54。最后,模型通过非极大值抑制去除重复边框,再把属于金刚石NV色心的概率小于0.5的边框去除,得到最终预测结果。

2 算法实现

2.1 数据集

本文采用的NV色心数据集都是来自量子实验平台对金刚石的扫描结果,从实验平台得到的数据是某个区域的计数率,在数据预处理阶段,本文把大于255的计数率置为255,从而得到灰度图作为输入图片。实验共收集了100张金刚石NV色心图片,其中70%作为训练集,30%作为测试集。

2.2 损失函数

模型的损失函数包含2个部分:① 先验框中包含目标的分类损失;② 先验框相对于真实边框位置的偏移形成的回归损失。对于一个先验框P,对应的真实边框为G,其类别为y∈{0,1},模型预测P的概率分布为f(P),P相对于G的偏移量为t=t(P,G),模型预测P的偏移量为g(P),则模型的损失函数为:

L(y,t,f(P),g(P))=Lcls(y,f(P))+λ[y≠0]Lloc(t,g(P))。

其中,Lcls为候选框的分类损失;Lloc为候选框的回归损失;λ为分类损失和回归损之间的平衡因子,本文取λ=1;[y≠0]表示只有类别为色心的先验框才计算回归损失,其表达式为:

对于分类损失,本文选择交叉熵损失函数;对于回归损失,模型不是直接输出修正后的边框,而是会对先验框的偏移量t进行建模。对于先验框P=(Px,Py,Pw,Ph)以及P对应的真实边框G=(Gx,Gy,Gw,Gh),两者的偏移量为t=(tx,ty,tw,th)。其中,tx=(Gx-Px)/Px;ty=(Gy-Py)/Py;tw=lb(Gw/Pw);th=lb(Gh/Ph)。

模型会输出对偏移量的预测值g(P)=(gx(P),gy(P),gw(P),gh(P))。因此,对于g(P)和回归目标t,本文采用smoothL1函数计算回归损失,即

其中

2.3 模型训练

采用Adam[14]的方法进行参数优化,Adam优化器的参数δ1、δ2为指数衰减因子,本文设置δ1=0.9,δ2=0.999,模型没有进行预训练,而是直接随机初始化参数。优化目标在损失函数的基础上加入L2正则化,即所有参数的均方和,正则化的平衡因子为0.000 4。初始化学习率为0.01,在整个模型收敛过程中,学习率按照指数方式衰减。

3 实验结果与分析

首先在测试集上运行模型,会输出一系列边框以及对应的概率分布,当边框区域为色心的概率大于某个概率阈值时认为该边框为色心。在概率阈值为0.5时3张图片的识别结果如图4所示。

从图4可以看出,对于不同目标数量和噪音大小,模型基本能够准确识别出金刚石NV色心目标。

图4 概率阈值为0.5时3张图片的识别结果

本文测试了在不同的概率阈值下,模型的召回率、准确率及F1值,结果如图5所示。

随着概率阈值的提高,模型的召回率下降,准确率上升,F1值先上升再下降;当概率阈值选择0.072时,模型的召回率与准确率相等,此时F1值最大,为95.5%;通常选择概率阈值为0.5,此时召回率为93.7%,准确率为97.3%,F1值为95.5%。

在测试集上对模型的性能进行综合评估,包括目标的召回率、准确率和平均准确率3个评价指标。模型会输出大量的边框和对应概率,然后根据交并比阈值和图片真实的边框进行匹配,最后计算模型的性能指标。

不同交并比阈值时的准确率-召回率曲线如图6所示。

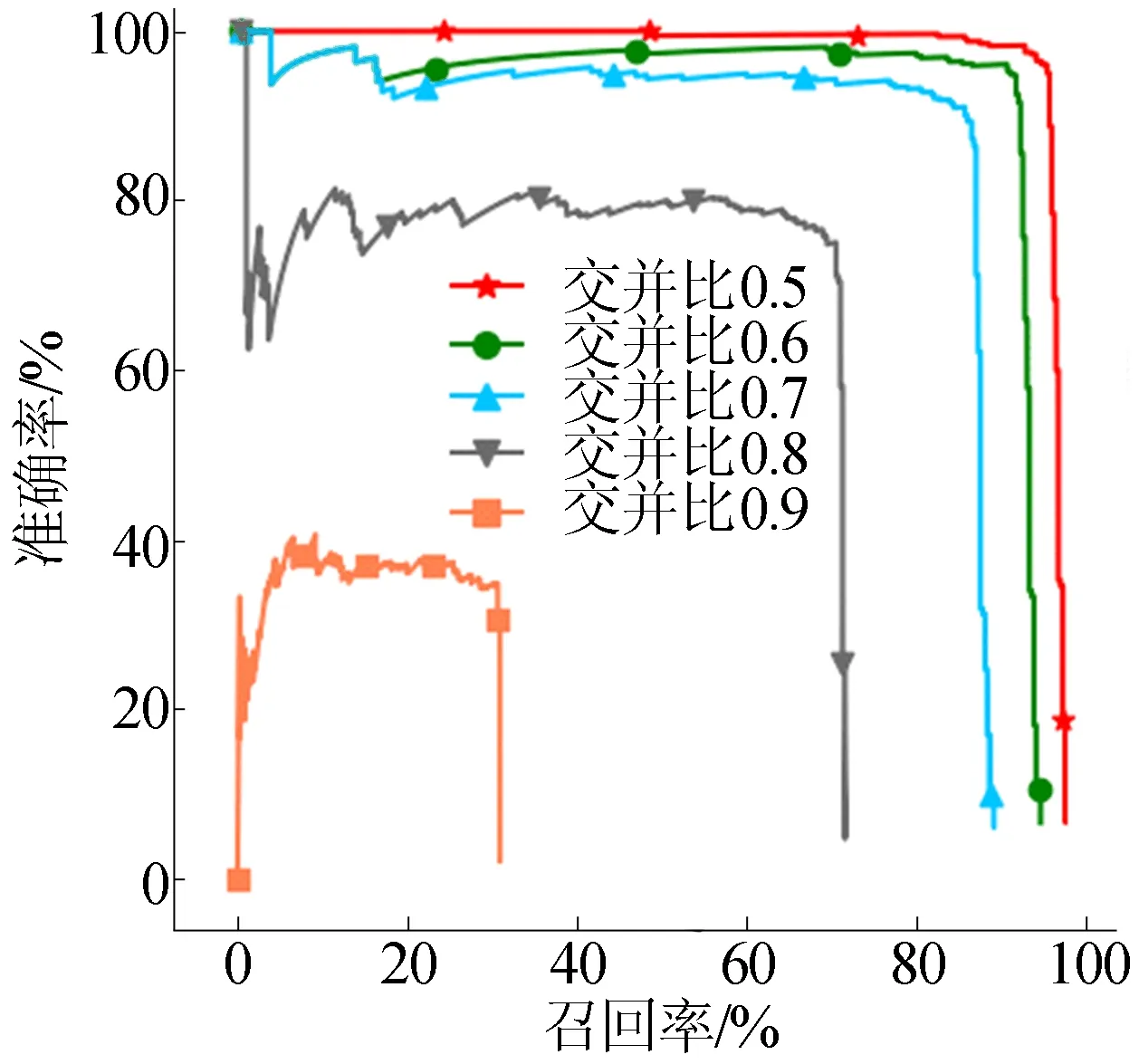
图6 不同交并比阈值下准确率-召回率曲线

从图6可以看出:

(1) 对于任意一条曲线,随着召回率的提高,模型的准确率都会下降;反之亦然。其原因在于计算准确率-召回率曲线时,会依次选择不同的概率阈值,为色心的概率大于这个阈值的边框预测为正例,随着阈值的降低,更多的边框被预测为包含色心,因此总能包含更多的真实色心目标,即召回率升高,但是会造成预测为色心的边框中其实不是色心,即准确率下降。

(2) 在交并比阈值取0.5、0.6或0.7时,模型能够同时具有较好的准确率和召回率,原因在于交并比阈值低意味着边框的匹配条件更宽松,因此召回率和准确率会更高;相反,在阈值取0.8或者0.9时,模型的准确率和召回率都迅速下降。

模型的平均准确率随交并比阈值的变化情况如图7所示。从图7可以看出,在阈值相对较低时,平均准确率接近于100%,随着阈值升高到1.0,平均准确率逐渐降低到0。通常选择阈值为0.5,此时模型的平均准确率为96.49%,表明模型完全能够兼顾准确率和召回率,具有较高的检出率以及很低的误检概率。

图7 平均准确率随交并比阈值变化曲线

4 结 论

本文针对金刚石NV色心目标自身噪音大、目标小等特点,使用卷积神经网络的方法,设计并搭建基础卷积网络进行特征提取,设计多任务损失函数并进行模型参数优化,最终实现了金刚石NV色心目标的自动识别。实验结果表明,模型具有较高的召回率和准确率以及平均准确率,这表明模型能够准确区分金刚石NV色心目标和噪音,与人工进行色心识别相比,大大提高了识别效果,提升了实验效率。

在量子实验平台上噪音受多种因素影响且无法完全避免,得到的色心图也多种多样,这对目标检测模型提出了更高的要求。本文需要进一步提升在各种噪音干扰情况下模型的适用性和健壮性,同时提高模型检测的速率,与原有平台软件进行整合,将识别算法与ODMR物理验证实验相结合,最终实现金刚石NV色心的在线自动识别。