二维水动力学模型糙率的推导和验证

郭晓明，乔 明

(1.丹华水利环境技术(上海)有限公司，上海，200235；2.浙江省环境科技有限公司，杭州，310007)

在数值模拟的计算中，糙率一般都是需要经过率定的[1-3]，即在某个糙率下数模结果与实测结果或试验结果进行比对，当相差较小时我们认为这个糙率就是模拟中可以使用的糙率。但是，在一些拟建的工程中如隧洞、渠道等，并无实测数据或试验数据，这时仅靠边壁的材料去确定糙率有失偏颇，特别在二维水动力学计算中会产生大的偏差。二维水动力学模拟中仅是考虑底部的影响，在模拟水深相对底部宽度比较大的隧洞和渠道时，直接用糙率系数表上的糙率进行计算的结果不准确，因此，需要增大河床单元格的综合糙率，以近似代表边壁糙率对流动的整体影响。

1 二维水动力学模型糙率的公式推导[4-7]

假定模拟无任何误差，那么二维数模计算出的流速等于实际的流速(即V′=V)。利用谢才公式和曼宁公式[8]：

两式联立可以得出：

谢才公式是根据明渠均匀流的实测资料总结的经验公式，在实际的工程中大多是阻力平方区的紊流，谢才系数的经验公式是根据阻力平方区紊流大量实测资料求得，所以适合我们的计算。

由于水力坡度相同，可以得出：

矩形过水断面情况下：

其中B为底部宽度；H为淹没深度。

2 二维水动力学模型控制方程[9]

二维水动力模型采用的公式如下：

质量守恒方程：

X方向动量方程：

Y方向的动量方程：

以上各式中，h为基准面下水深；u、v分别为沿X、Y方向的流速；t为时间；η为床面高程；g为重力加速度；Exx、Eyy、Exy为涡动扩散系数；a为河床高程；n为曼宁糙率系数；ζ为风应力系数；Va为风速；ψ为风向；ω为地球角速度；φ为当地纬度。

3 糙率公式验证

为了验证推论的合理性和正确性，我们用下庄电站引水设计的物理模型试验结果和藕节水槽试验结果及矩形水槽水力计算结果与二维数值模型的计算结果进行对比。

3.1 下庄电站引水设计[10]

下庄电站位于岷江支流杂谷脑河下游河段左岸，为杂谷脑河规划十八级梯级电站中的第17级电站。由取水枢纽、泄洪闸、冲砂闸、冲砂槽、进水口、引水明渠、泄水道等建筑物组成。取水枢纽设计洪水流量916m3/s，校核洪水流量1180m3/s。为了更好地发挥电站的经济效益和在灾后重建中的作用，对电站引水系统进行技改，在原有杂谷脑河引水明渠旁开挖引水隧洞，引水隧洞采用马蹄形断面，底部宽度为6.6m，内部流动为无压水流。

根据下庄电站的位置和所拥有的实测资料及需要计算的范围，我们选取的模拟区域长约为1.47km，河道段长140m，引水隧洞和引水明渠长平均1.33km。采用三角形网格与四边形网格离散计算区域，在交汇处及不规则区域主要采用三角形网格，其它则采用四边形网格，模拟区域网格共12265个，其中三角形网格1314个，四边形网格10951，节点38029个。

引水隧洞断面为马蹄形断面，但在二维数值计算中近似取为矩形断面。上游给以流量，下游给以水位边界条件。在上游来水为160m3/s时，关闭所有的泄洪闸，下游控制水位为1403.5m(前池正常水位)。根据材料不同查出的初始糙率取值为：杂谷脑河率定糙率n=0.035；原引水明渠n=0.018；引水隧洞n=0.014。经过计算新建引水隧洞内平均水深约为4.3m，原引水明渠内平均水深约为3.5m。引水隧洞底部宽度为6.6m，引水明渠底部宽度为7.7m。

图1 网格结构

再根据修正后的糙率进行模拟，得出闸前断面CS1的水位对比和沿隧洞内前300m的水深，分别见图2和图3。

图2 闸前水位对比

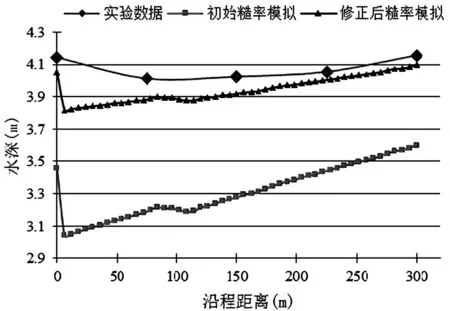
图3 隧洞内水深对比

用初始的糙率进行计算的结果和实验数据相差很大，但是用经过修正后的糙率进行计算的结果和试验数据相差很小。图2可以看出，未经修正糙率模拟的闸前水位与试验数据相差60cm，而经过修正后相差不到5cm；图3中的未经修正糙率模拟的水深相差50cm以上，但是经过修正后水深相差大幅缩小。另外，由于公式中所用水深为初始糙率进行模拟的结果，在用计算修正后糙率时使水深偏小，故可以用修正后糙率模拟出的水深重新计算糙率，会更加合适。

3.2 藕节水槽试验

在四川大学水力学国家重点实验室做的藕节水槽试验，水槽长28m，坡度为0.002，有三个藕节，最宽为1.4m，最窄为0.6m，深为0.5m，材质采用抹面混凝土。模拟中取15.2m的长度，示意图如图4。

图4 藕节示意

网格为四边形网格共2000个，节点数为6421个。网格分布图如图5。

图5 藕节网格划分

进口给定流量为100L/s，出口给定水位为10.18cm，根据试验中底部和壁面的材料，经过查询吴持恭《水力学》糙率系数表，糙率取0.013。关于E的取值比较关键，在水深较浅时E应该尽可能的小，在模拟中E取25Pa/s。根据初始单一糙率0.013模拟的水深，以及不同的底部宽度可以得出修正糙率沿程的变化。

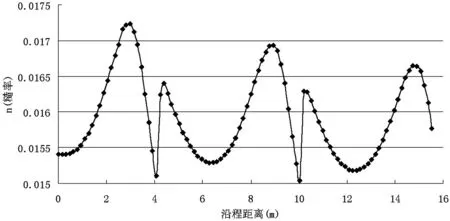
图6 糙率沿程分布

然后根据糙率把模拟段分为8个部分，每个区域糙率取平均值，其值在0.0158～0.0165之间，相差较小。再根据修正后的糙率进行模拟，得出模拟段内的水位。

图7 沿程水位对比

可以看出，当采用糙率0.013时其在收缩处的水位变化极大，且和实验数据差别很大，达到4cm；当采用修正后的糙率时其差别缩小，在收缩处不到1.5cm。

3.3 理想矩形水槽

设定一个长100m，宽10m，底部坡度为1/1000的矩形水槽，糙率为0.04。假设过水流量为100m3/s、200m3/s、300m3/s，矩形水槽流动为均匀流。可以通过谢才公式和曼宁公式得出：

通过试算，可以得出三个流量对应的水深H分别为6.37m、11.09m、15.62m，流速V分别为1.57m/s、1.804m/s、1.92m/s。上游进口处给定流量，下游出口给定水位(出口处地形高程为0，故水位即水深H)，对矩形槽进行模拟。计算中E取2000Pa/s。

图8 网格及平面示意

由于水深变化较小，可以直接用下游出口水深修正糙率。

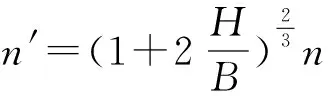
代入H=6.37m、11.09m、15.62m。可以得出三个修正糙率分别为0.0692、0.0872、0.1029。根据三种不同的工况和不同的糙率进行模拟。水位、流速沿程变化图如图9。

(a)流量100m3/s时流速沿程变化 (b)流量100m3/s时水位沿程变化

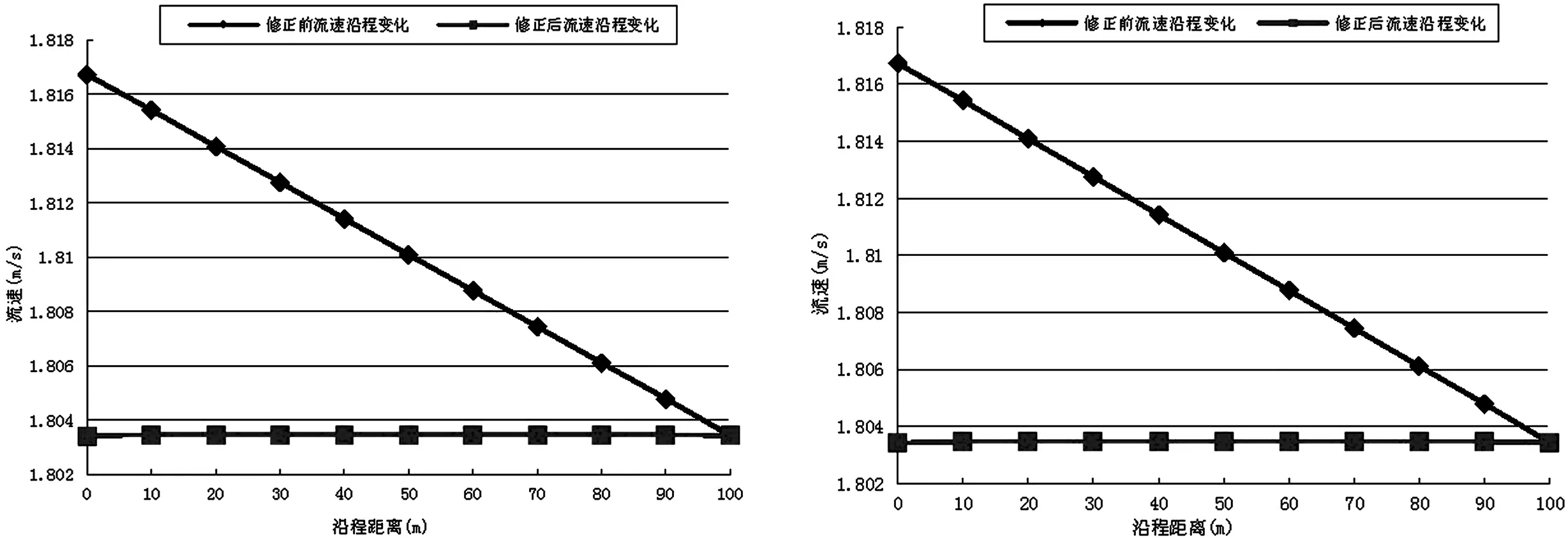
(c)流量200m3/s时流速沿程变化 (d)流量200m3/s时水位沿程变化

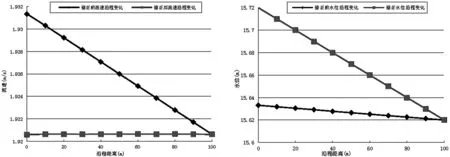
(e)流量300m3/s时流速沿程变化 (f)流量300m3/s时水位沿程变化

根据均匀流的定义，水力坡度应该与底部坡度相一致且流速不发生变化。从图9中可以看出，在流量100m3/s、200m3/s、300m3/s情况下，根据矩形槽糙率0.04所模拟出的水力坡度约为3/10000，远远小于底部坡度1/1000。而用修正糙率计算的结果完全符合均匀流的定义，上下游水位差0.1m，水力坡度1/1000。修正前流速沿程逐渐减小，修正后流速与均匀流公式计算出的几乎完全一致，相差不到0.001m/s。

3.4 验证结果分析

我们本可以通过试验得出糙率的率定，但是不经过率定而直接通过糙率修正公式进行糙率的选取也可以得出满意的结果，这就为如果没有实测数据及试验数据的河道、渠道、隧洞等计算提供了好的糙率修正准则，将大大改进数模计算的质量。

在藕节模拟中，由于断面的收缩扩张，水流流态变化大，流动为恒定非均匀流，导致修正后的模拟数据与试验数据存在偏差，但是通过修正后的糙率值相比直接用糙率系数表中的糙率有较大的改进。在下庄电站引水的模拟中，隧洞和明渠中的流态近似渐变流，流态比较稳定，修正后的模拟效果更好。理想矩形水槽的数模结果与矩形水槽均匀流公式计算结果完全一致。修正公式对于均匀流和渐变流有较好的结果。

4 结论

在二维水动力模型计算中，隧洞和渠道等由于缺少实测资料和试验资料，不能对其进行准确的率定。我们可以通过查糙率表，通过公式计算得出模型需要的糙率。公式更加适合于宽深比较大的渠系，公式为二维水动力模型计算采用糙率提供参考。即使修正后的糙率还是有一定的差别，因为修正公式使用范围是恒定均匀流或渐变流。