不同高度重力数据和井中重力数据融合反演研究

高秀鹤,熊盛青,于长春,孙思源

(1.中国自然资源航空物探遥感中心, 北京 100083; 2.自然资源部 航空地球物理与遥感地质重点实验室, 北京 100083；3.中国地质大学(北京) 地球物理与信息技术学院, 北京 100029)

0 引言

重力数据反演面临严重的多解性问题，高斯定理指出其本质原因：有无数种不同的密度分布可以引起相同的重力异常[1-3]；此外，异常体引起的重力异常是连续分布的，而我们采集的信息只是某一平面上的部分离散数据，这种信息量的不足进一步加重了反演结果的多解性[4-5]。这种多解性是导致重力数据反演结果趋肤效应严重、分辨率低的本质原因。利用已知的先验地质信息对密度进行合理约束是改善重力数据反演效果的有效手段，常用的约束方法有最小质量约束、最小体积约束、最大光滑约束、最小惯量约束等[6-10]。另一方面，增加观测数据的数据量也能够改善反演效果[11-12]，增加的观测数据可以是同种地球物理数据加密或不同平面采集，也可以是不同种类地球物理数据[13-14]。但在实际工作中，由于经费或者测量条件限制，无法获得更多观测数据时，通过延拓技术获取多高度面观测数据加入到反演中是可行的[15]。

垂直分辨率差是重力数据反演中最为突出的问题[16]，重力数据的核函数随深度的增加逐渐衰减是密度反演结果分辨率差的直接原因。从方法技术角度出发，引入深度加权抵消核函数衰减速率，能够有效克服反演结果的趋肤效应，提高垂直分辨率[3,17-19]；从实测数据角度出发，引入邻近异常源的井中观测重力数据、井中岩石密度数据，可提高反演结果的垂直分辨率[20]。

不同高度观测面的重力数据包含的波场信息不同[21]，因此，单独反演效果存在差异，本文首先设计模型试验分析了不同高度面观测重力数据的反演效果；然后，融合反演不同高度面观测的重力数据，与单一高度面观测重力数据反演结果对比，分析融合反演的效果，同时，多观测面数据不可得时，利用延拓技术获得不同高度重力数据用于反演；最后，分析井中重力数据、井中密度数据约束下，不同高度重力数据反演效果。

1 融合反演原理

离散重力数据与离散密度块体的关系如下：

g=Aρ，

(1)

式中：ρ是密度向量，g是某一观测面的观测重力数据向量，A是正演算子矩阵。反演过程中，已知观测重力数据向量g和正演算子矩阵A，求解密度向量ρ。由于观测数据中不可避免含有噪声干扰，使得反演问题病态，导致解不稳定，吉洪诺夫正则化方法作为一种常规的处理手段，可有效解决这一问题，求式(1)中ρ的反演问题可转化为求解目标函数最优解的问题，目标函数如下：

φ=φg+αφρ，

(2)

式中：φg是数据拟合函数，φρ是模型拟合函数，α代表正则化参数。数据拟合函数为

(3)

模型拟合函数为最小模型约束：

(4)

在模型拟合项中加入深度加权函数W，可有效克服重力反演结果中的趋肤问题。反演结果中异常体的埋深很大程度上受深度加权函数影响，弱的深度加权函数容易获得较浅的异常体埋深，强的深度加权则容易获得较深的异常体埋深。

引入深度加权函数后，模型拟合函数可以写成

(5)

不同平面(高度或深度为z)重力数据融合反演时，数据拟合函数不同。观测重力数据gz表示观测面高度或深度为z的重力数据。将gz作为观测数据加入到目标函数的数据拟合函数中，则数据拟合函数为

(6)

式中：Az是与gz对应的正演算子矩阵。此外，还可以在数据拟合函数中加入井中重力数据gb、井中岩石密度数据ρd，则有

(7)

其中：gb代表井中重力数据，Ab是与gb对应的正演算子，ρd代表井中岩石密度数据，Ad可以看成是与ρd对应的正演算子，它是一个稀疏矩阵，矩阵每行仅有一个非0元素，与取样岩石位置有关，其值为1。式(7)所示的数据拟合函数加入到目标函数中，可实现不同高度观测面、井中数据的融合反演，通过调整系数λ1、λ2、λb和λd的大小可调整不同高度面观测重力数据、井中重力数据、井中岩石密度数据对目标函数的作用大小：系数越小，相应数据对目标函数影响越小；系数越大，相应数据对目标函数影响越大；当系数为0时，相应数据对目标函数不起作用，即相应数据不参与反演过程。

2 模型试验

2.1 模型一：单立方体模型

为了验证不同平面观测重力数据三维反演效果，建立一个立方体模型，如图1a所示，立方体模型的大小为400 m×400 m×400 m，顶面埋深为300 m，中心位置为(2.5 km, 2.5 m, 0.5 km)，密度差为1 g·cm-3，背景密度为0。将地下三维空间剖分为50×50×15个大小为100 m×100 m×100 m的立方体单元，50×50个观测点位于每个单元的中心。正演计算得到的不同高度观测面的重力数据如图1b、c、d、e、f所示。

利用正则化方法反演不同高度面观测重力数据。为了对比反演效果，对于不同高度面的观测重力数据反演，引入相同的密度上下限 (0, 1 g·cm-3)和相同的模型加权函数W=(ATA)1/2，其中，A表示地面重力数据的正演算子。利用共轭梯度算法迭代求解目标函数最优解，得到的反演结果切片如图2所示。观测面高度越高，相应的反演结果越发散；观测面高度越低，相应的反演结果越收敛，且反演结果与理论模型的分布范围、密度值大小越接近。

不同高度面的观测重力数据融合反演结果如图3所示。图3a与图2c相比，由于地面以下300 m观测数据的加入，密度分布更收敛，密度值更接近理论密度值；图3a与图2f相比，由于地面观测数据的加入，压制了异常体两侧的假异常。这初步验证了不同高度面观测重力数据融合反演的良好效果。相比于图2c，图3a显然与图2f更接近，说明近源平面数据对反演结果影响更大。图3b与图2b、d相比，密度分布更收敛，密度值更接近理论密度值，与图2f相比，压制了异常体两侧的假异常。这再次验证了不同高度面观测重力数据融合反演的良好效果。图3c与图3b相比，增加了两个面的观测数据，反演效果并未见明显提高。这说明为保证计算效率，需选择适当、适量平面的观测重力数据进行融合反演，过多的数据将导致计算量增大，但反演效果并没有明显的提高。

仅有一个观测面的重力数据时，可通过延拓技术得到多个不同高度面的延拓重力数据。使用延拓数据反演需注意几个问题:一是为提高反演效果，使用向下延拓重力数据进行反演，原因是：单个平面重力数据反演验证，观测面高度越低，反演效果越好；二是为保证反演可靠性，下延平面应高于异常体顶面，原因是：穿过或低于异常体的延拓数据不准确，不适合用于反演；三是为了拟合原始观测重力数据，使用延拓数据与原始观测数据融合反演，原因是：向下延拓得到的重力数据存在误差，单独反演延拓数据将导致反演结果可能无法拟合原始观测数据。

图1 立方体模型及正演重力数据Fig.1 Cube model and its forward gravity data

图2 不同高度面观测重力数据单独反演结果的竖直切片(y=2.5 km) Fig.2 Vertical slices of inversion results of gravity data at different heights

图3 不同高度面观测重力数据融合反演结果的竖直切片(y=2.5 km)Fig.3 Vertical slices of inversion results of joint gravity data at different heights(y=2.5 km)

观测重力数据及其延拓重力数据融合反演结果如图4所示，图4a与图3a相比，密度分布较发散，密度值较小，这是由于向下延拓数据中存在误差，说明延拓数据不能取代观测数据；与图2c相比，密度分布更收敛，密度值更接近真实密度值，反演效果明显提高，这说明，在多平面数据不可得时，延拓数据的加入可提高反演效果。图4b与图3b相比，密度分布较发散；但与图2b相比，反演效果明显提高，再次验证了加入延拓数据的意义。图4c与图4b对比，反演效果提高并不明显。因此，为保证计算效率，选择适当、适量的延拓数据加入反演是至关重要的，过多的延拓数据导致计算量增大，但反演效果并没有明显提高。

图4 观测重力数据及其延拓重力数据融合反演结果的竖直切片(y=2.5 km) Fig.4 Inverted density models using the joint observed gravity and continuation gravity data(y=2.5 km)

利用单立方体模型验证加入井数据约束对反演效果的影响。模拟设计3口竖直井，3口竖直井分别位于立方体中心、立方体外100 m、立方体外300 m，其坐标分别为(2.5 km,2.5 km)、(2.8 km,2.5 km)、(3.0 km,2.5 km)。井中观测重力数据、岩石密度数据如图5所示。在地面、地面以下300 m重力数据融合反演中，分别加入3口井数据做约束，得到的反演结果如图6所示。与图3a相比，反演效果明显提高，这说明加入位于立方体中心的井数据做约束可有效改善反演效果；加入位于立方体外100 m的井数据做约束对邻近井位的密度分布有一定改善作用，对整体反演结果影响较小；加入位于立方体外300 m的井数据做约束对反演结果的影响很小。这说明，井口穿过异常体，能有效改善反演效果；井口距离异常体越远，对反演效果的有益影响越小。

图5 不同位置井的井中重力和岩石密度Fig.5 Well gravity and well density at different locations

图6 地面、地面以下300 m重力数据和井中重力、岩石密度数据融合反演结果(白色实线代表钻井位置)Fig.6 Recovered density models in the constraint of well data(the solid white line represents the drilling location)

2.2 模型二：双长方体模型

为进一步验证不同高度重力数据和井数据融合反演的效果，设置不同埋深的双长方体模型，左侧长方体顶面埋深300 m，中心位置坐标为(550 m,1 050 m,500 m)，大小为300 m×300 m×400 m，密度为1 g·cm-3，右侧长方体顶面埋深为500 m，中心位置坐标为(1 350 m,1 050 m,700 m)，其大小、密度与左侧长方体相同。地下空间剖分为38×42×15个大小为50 m×50 m×100 m的立方体单元，38×42个地面观测数据采样间距为50 m，井中观测数据采样间距为50 m。加入3%的高斯噪声的正演理论地面重力数据如图7a所示，将地面重力数据向下延拓300 m 得到的延拓重力数据如图7b所示。模拟两口竖直井：井A、井B，其水平位置分别为(550 m,1 050 m)、(1 350 m,1 050 m)，即位于两个长方体中心，填加3%高斯噪声的井中重力、岩石密度数据如图8所示。

地面重力数据单独反演结果如图9b所示，左侧埋深较浅的异常体中心位置识别准确，右侧埋深较深的异常体未被有效识别，且无法区分两个异常体，反演结果整体较为发散，分辨率较低。加入向下延拓300 m重力数据与地面重力数据融合反演结果如图9c，与图9b相比，左侧异常体中心位置定位准确，且异常体边界清晰，密度值的最大值达到真实值，右侧异常体反演效果仍不理想，且由于下延数据中噪声很大，导致反演结果中也出现了假异常。再加入两口井的井中重力、岩石密度数据约束，反演结果如图9d，准确定位了两个不同埋深的异常体的中心位置，边界清晰，分辨率高，两个异常体的最大异常值都达到了理论值，与图9a所示的理论模型剖面匹配度较高。

图7 双长方体模拟重力数据Fig.7 Gravity data based on double prisms

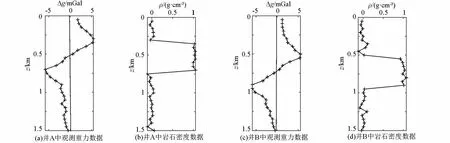
图8 含3%高斯噪声的模拟井中观测数据Fig.8 The simulated data observed in the wells

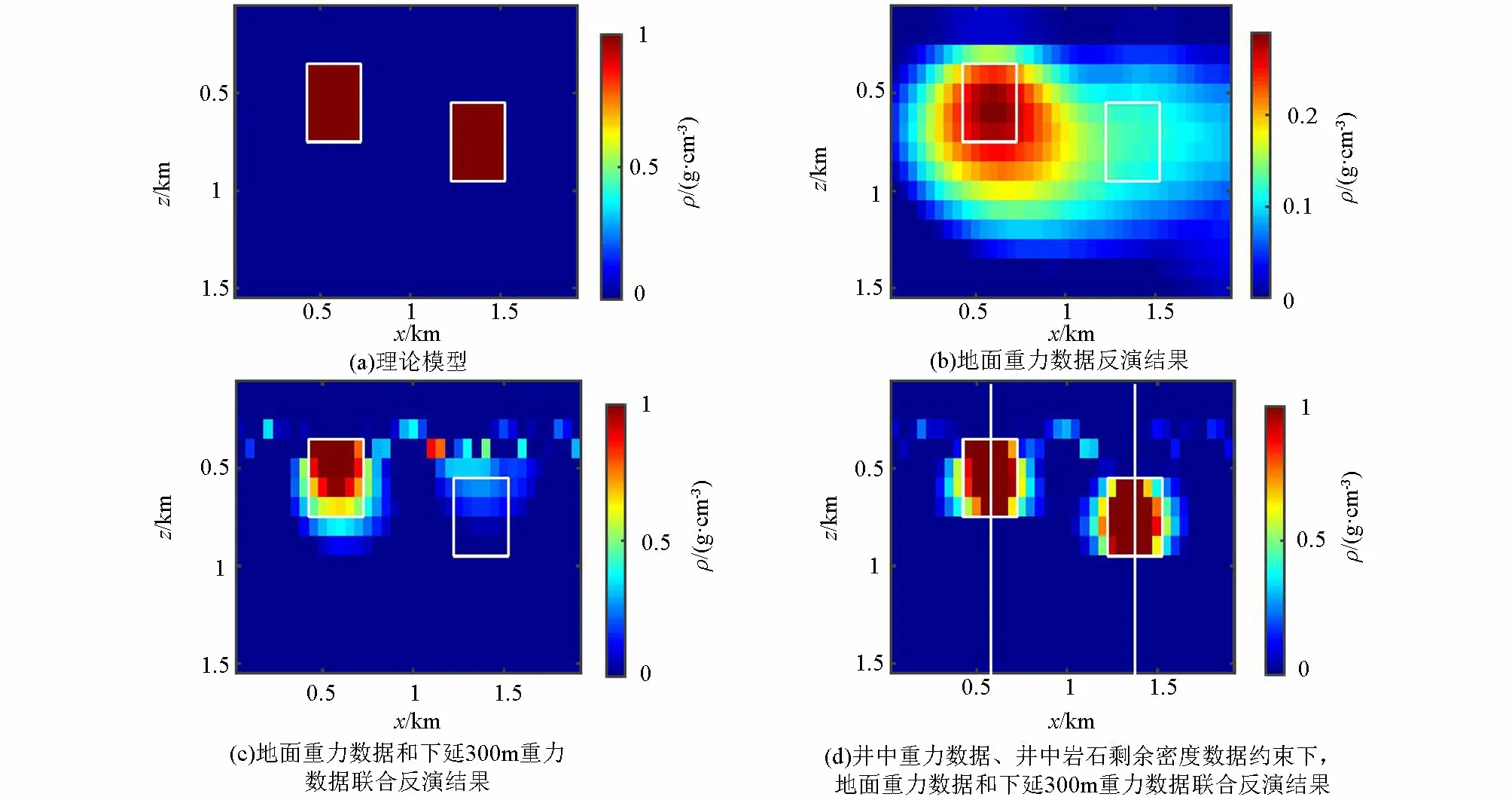
图9 双立方体模型反演结果 (白色实线代表钻井位置)Fig.9 Recovered double-prism models(the solid white line represents the drilling location)

3 结论

1) 单一观测面重力数据三维反演效果与测量面高度有关，观测面高度越低(观测面距离异常源越近)，反演效果越好。

2) 与单一观测面重力数据反演相比，多个高度面观测重力数据融合反演的效果可得到改善，其中，近源高度面数据比远源高度面数据对反演结果影响大。

3) 过多个观测面的重力数据对反演效果改善不明显，因此，为保证计算效率，应选择适当、适量的观测面的重力数据进行融合反演。

4) 当多个高度面的观测重力数据不可得时，通过向下延拓技术可得到多个平面的延拓重力数据(延拓平面应高于异常体顶面)，观测重力数据与向下延拓重力数据融合反演，也可改善反演效果。

5) 井中重力、岩石密度数据约束，可一定程度改善反演效果，改善程度受钻井位置影响明显，穿过异常体的井数据可明显改善反演效果，钻井位置距离异常体越远，对反演效果影响越小。