硅微谐振式加速度计温度自补偿方法研究

刘泽畅 熊兴崟 蔡朋成 邹旭东

摘要：硅微谐振式加速度计具有低功耗、高灵敏度等优点，在导航、测控等领域有着广泛应用。温度误差会导致输出频率产生漂移，从而影响硅微谐振式加速度计的精度。本文基于硅微谐振式加速度计的特点，提出了一种硅微谐振式加速度计温度自补偿实现方法，通过研究加速度计的工作原理，对加速度计输出频率建立二元函数模型，利用反拟合法反解出实际的加速度值。设计基于FPGA的硬件实现方案，实现温度自补偿方法，达到对硅微谐振式加速度计进行实时温度补偿的目的。

关键词：MEMS 加速度计 温度补偿 FPGA

Study on Temperature Self-Compensation Method of Silicon Resonant Accelerometer

LIU Zechang1，2  XIONG Xingyin1  CAI Pengcheng1  ZOU Xudong1*

（1.Aerospace Information Research Institute， Chinese Academy of Sciences， Beijing， 100190 China;

2. University of Chinese Academy of Sciences， Beijing， 100049 China）

Abstract： Silicon resonant accelerometer has the advantages of low power consumption and high sensitivity. It is widely used in navigation， measurement and control and other fields. Temperature error will cause the output frequency to drift， which will affect the accuracy of silicon micro resonant accelerometer. In this paper， a temperature self-compensation implementation method of silicon resonant accelerometer is proposed based on its characteristic. By studying the working principle of the accelerometer， a binary function model is established for the output frequency of the accelerometer， and the actual acceleration value is solved by using the reverse fitting method. The hardware implementation scheme based on FPGA is designed to realize the temperature self-compensation method and achieve the purpose of real-time temperature compensation for the silicon -resonant accelerometer.

Key Words： MEMS; Accelerometer; Temperature compensation; FPGA

硅微谐振式加速度计是一种惯性传感器，它的原理是根据测量得到的谐振频率输出信号，求得相应的加速度，主要具备灵敏度高、易集成和低功耗等优点。硅微谐振式加速度计是一种对温度变化十分敏感的器件。当工作环境温度发生变化，传感器的灵敏度和加速度敏感程度都会受到影响，由此产生温度漂移，导致输出加速度值发生偏差。

针对谐振器结构等方面的不同，可以采用不同的方法来解决温度漂移问题：结构层面，从改进结构、优化加工工艺入手;电气层面，可以从源头控制工作温度入手，也可以从建模并结合外部温度传感器的方法来补偿温度漂移。传统的建模法中，通常利用外部温度传感器测温建立模型，但这种方法由于温度传递误差的存在，无法测得准确反映内部温度的真实温度值，因此无法实现高精度补偿。

因此，本文在建模法的基础上，利用加速度计谐振器的自身的性质，在无需外部温度传感器的情况下，对输出加速度进行温度自补偿。在分析所用差分结构加速度计的温度特征的基础上， 建立加速度计输出频率与输出加速度及温度相关的自补偿模型。设计直接解算加速度的求解方法，结合FPGA硬件平台实现温度自补偿算法。

1 硅微谐振式加速度计温度自补偿方法

温度自补偿算法原理

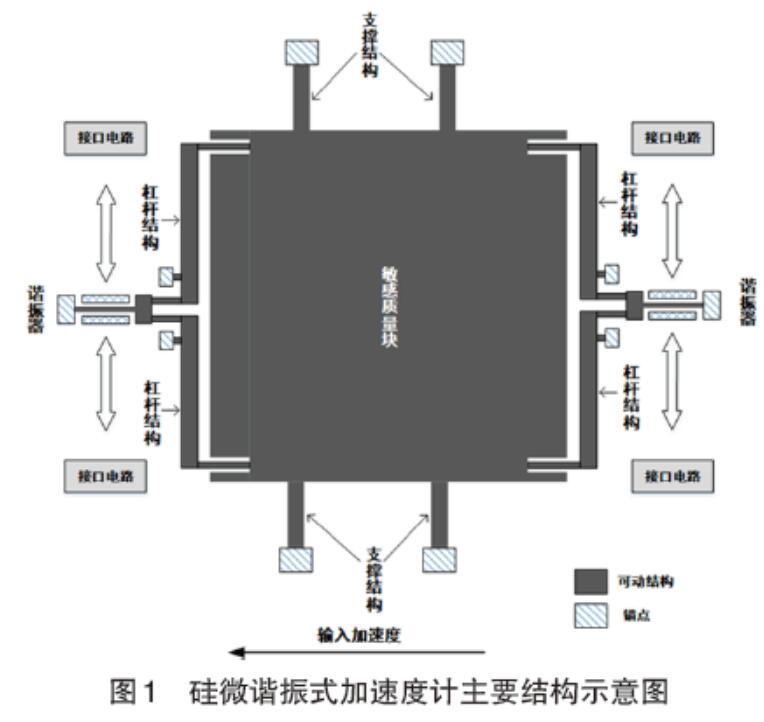
图1所示为本文所采用的硅微谐振式加速度计主要结构示意图，主要包括谐振器结构、杠杆结构、驱动检测结构、虚拟静电力加载装置、敏感质量块以及其支撑结构等。

加速度计连接方式为：敏感质量块由支撑结构支撑，支撑结构的支撑梁为悬臂梁，其一端与敏感质量块相连，另一端通过锚点固定;虚拟静电力加载装置安装于敏感质量块的中心;杠杆结构的输入梁和敏感质量块相接，输出梁与谐振器的一端相连[1]。

谐振器结构包括谐振梁、驱动电极、检测电极和锚点，谐振梁一端与杠杆结构输出梁一端相连，另一端与锚点相连。谐振梁用于感受杠杆结构输出梁传导过来的应力变化，从而改变谐振频率;驱动电极、检测电极和接口电路连接，驱动谐振梁谐振，同时检测谐振梁位移。驱动电极、检测电极和谐振梁共同构成平行板执行器结构。

当外界的惯性力产生加速度时，敏感质量块受到外界加速度作用，敏感质量块在敏感轴方向受到惯性力的作用，該作用力通过微杠杆放大后施加在加速度敏感谐振梁上，从而改变该谐振梁的谐振频率。其中一个谐振器的输出频率会因为受压应力而变小，另外一路谐振器的输出谐振频率则会因为受拉应力而增大，测量两端的差分谐振频率，就可以计算得出输入加速度的值。

由于两个谐振器在同一芯片上且使用相同工艺制作而成，所以它们具有相似的频率温度系数。此外，该加速度计尺寸非常小，两个谐振器相距较近，所处的温度梯度相同，即在相同温度下产生的频率漂移相同[2]。这一点是本课题的温度自补偿研究的重要理论基础。

在有外界加速度输入时，关于硅微谐振式加速度计两路输出频率的关系式中，既有加速度项，又有温度项[3]。加速度项系数为比例因子SF，温度项系数为频率温度系数。当外界产生惯性力，对加速度计施加加速度产生谐振频率时，谐振频率若写作二元函数，就是与加速度项和温度项相关的二元函数，同时考虑两路差分谐振器的输出，就是二元函数方程组。当我们设计加速度计时，取工作量程在比例因子的深線性区间内，也就是加速度项的比例因子取作常数，第一谐振器和第二谐振器的比例因子分别为SF1和SF2.

当外界产生惯性力，对加速度计施加加速度产生谐振频率时，梁的形变导致两路谐振器受力方向不等，则两路谐振器输出频率可表达为：

{█（&f_1=f_10 （T）+SF_1⋅a@&f_2=f_20 （T）-SF_2⋅a）┤

f1，f2为两路谐振器频率信号，f_10 （T），□（ ） f_20 （T） 为频率温度项，SF为比例因子，a为实际输出的加速度值。

1.2 温度自补偿模型建立

通过前一小节的原理分析得知，谐振器输出频率与加速度和温度两个自变量相关。因此，我们需要研究谐振器的频率温度特性，从而确定频率温度项的具体模型。

建立谐振器输出频率模型中频率温度项的一元函数关系，考虑其具有一定的非线性[4]，得到频率温度方程组模型如下：

{█（&f_10=k_10+k_11 T+k_12 T^2+……@&f_20=k_20+k_21 T+k_22 T^2+……）┤

其中，f10，f20为没有外界惯性力导致产生加速度（即a=0）时两路谐振器输出频率，k为各阶温度系数。

根据频率温度方程组模型特征，提取需拟合的多项式形式：

y=a_0+a_1 x+a_2 x^2……+a_k x^k

对现有加速度计进行了频率温度特性实验，实验平台主要包括实验室直流电源，网络分析仪，温控箱、转台、测温铂电阻、加速度计及其驱动电路等表等。直流电源型号为KEYSIGHT U8032A，网络分析仪型号为KEYSIGHT E5061B。

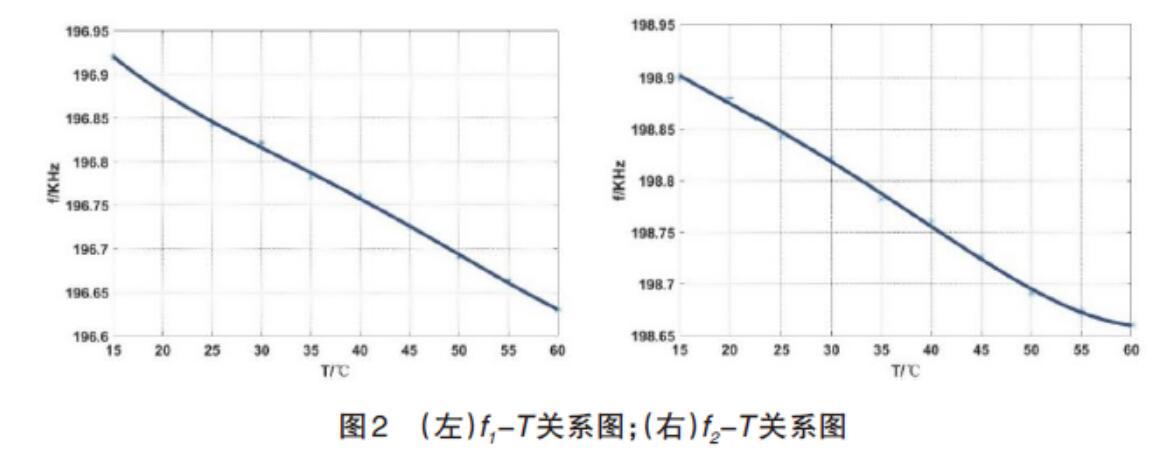
在输入加速度为零的情况下，通过温控箱控制温度，在全温范围-40℃～60℃范围内，每隔10℃取一个温度点，一共11个温度点下测试加速度计输出频率，得到加速度计输出频率与环境温度关系：

对测试结果进行分析，可以看出：加速度计的两路差分谐振器固有频率随温度的变化趋势几乎一样，都是随着温度的升高而降低，且频率温度系数非常接近。频率随温度的变化大致为总体线性关系，但同时也与温度满足一定的非线性关系。为了求解关系进行温度补偿，通常采用曲线拟合的算法[5]。

在MATLAB中分别进行线性、二阶、三阶和四阶拟合，可以得到不同阶数的多项式的系数。计算拟合残差，结果表明：随拟合阶数的增加，拟合残差基本是在减小，四阶模型的拟合残差相对三阶没有明显的提高。因为在温度自补偿设计中，需要对拟合精度和计算速度作出权衡与兼顾，所以我们使用频率温度的三阶多项式模型来实现建模算法。

为了标定比例因子，通过温控箱控制加速度计所处环境温度保持在恒温30℃，调整安装有加速度计的转台的角度，从90°到-90°每隔10°取一个加速度标定点，在每个标定点记录对应的输入加速度值及加速度计输出频率值[6]。

经过数据处理及MATLAB拟合，得到两路谐振器输出频率与加速度关系曲线基本呈线性，计算得到SF1=534Hz/g，SF2=498Hz/g。计算拟合残差，残差计算结果显示，两路谐振器均具有良好的线性度，因此，在温度自补偿计算中，直接将比例因子标定值SF1=534Hz/g，SF2=498Hz/g作为加速度项系数，进行温度自补偿。

温度自补偿实现方案

加速度求解方法

经过上述步骤，我们得到了完整的加速度计温度自补偿模型。采用反拟合法来求解加速度值，即：在已知模型中各项系数的情况下，取一定范围内的n个温度值及m个加速度值，计算出n×m组输出频率值（f1，f2），然后对加速度与两路谐振频率建立模型如下：

a=p_0+p_1 f_1+p_2 f_2+p_3 f_1 f_2+p_4 f_1^2+p_5 f_2^2

基于上式，对加速度a与f1、f2进行拟合，得到该反解加速度公式中的系数p0～p5，那么在硅微谐振式加速度计的实际补偿中，实时测量两路谐振器频率，再结合拟合模型中的系数，即可得到实际的加速度值。

采用最小二乘法，分别对上式的四项式、六项式和八项式进行最小二乘拟合，得到加速度解算式的系数，并计算拟合残差进行比较。四项式、六项式及八项式之间拟合系数差别较大。在这三种多项式中，四项式非线性项只有一项，因此模型在六项式与八项式之间选定。

要确定究竟用六项式模型还是八项式模型，我们利用MATLAB分别求解它们的剩余标准差RMSE（Root mean squared error，即均方根误差）。在误差分析过程中，实际数值和估计的理论数值之间存在误差，该误差被叫做残差或剩余量，在此基础上，对全部的残差平方进行求和，得到的结果被称为残差平方和或剩余平方和。对剩余平方和进行开平方计算，就可以得到剩余标准差，用来表示估计值的精度。

在MATLAB中，利用公式rmse=sqrt（（sum（（a-b）.^2））./2，分别解算得到六项式拟合及八项式拟合的剩余标准差为25.6μg和28.17μg。由此可见八项式拟合剩余标准差较大，且计算复杂，在实际硬件实现中必定占用更多资源。

在完成上述误差分析过程后，我们最终确定六项式关系来进行解算实际加速度值。

基于FPGA的硬件实现方案

在实际应用过程中，若要实现对加速度值的解算，需要借助硬件平台的计算、存储等资源进行实现。解算加速度所需的两路谐振频率信号可以通过测频得到，那么将测频模块的输出作为加速度解算模块的输入，可以完成加速度求解过程。本文选择基于FPGA硬件平台，设计温度自补偿方法的实现方案。

在硬件实现中，如何获得高精度谐振频率并进行后续参数补偿是关键问题之一。所用的测频方法至关重要。本文采用对方波信號进行计数的数字方法实现测频需要，然后根据采集得到的频率值求解加速度，那么在FPGA配置与选型时，需要选择内部资源满足整个温度补偿方案实现系统的需求的 FPGA 芯片，写入频率测量算法，完成频率采集，输入加速度解算模块，调用计算资源完成解算，最后通过数据串口传输至上位机，测得加速度信息。

目前广泛应用的测频方法中，包括几种基于计数法的高精度测频算法，如直接计数法，延迟链法以及多周期同步计数测频法等。后两者相较于最普通的直接计数法而言，精度有明显的提升，而这两者相比较，延迟链法的测频精度更高，比多周期同步计数法的误差要小，但缺点在于各单元实现时，由于延时的存在很容易出现误差。因此，频率测量模块选择多周期同步计数法实现，实现方式简单，易于提升精度。

具体方案设计如下：加速度计输出频率信号（未补偿）经由AD转换变成数字量进入FPGA芯片，通过多周期同步测频法采集两路频率信号，完成对f1、f2的测量。将反解加速度的计算式中的系数p0～p5存入FPGA内部的寄存器，然后通过调用FPGA自带的乘法器、加法器，将系数和两路频率信号按照反解加速度的计算式进行乘加运算，得到实际的加速度值。

温度自补偿效果验证实验

对本文中的温度自补偿方法补偿效果进行验证：在加速度计的输入加速度恒为1g的情况下，通过温控箱控制温度，在全温范围-40℃～60℃范围内，每隔10℃取一个温度点，一共11个温度点下记录加速度计输出的两路谐振频率值。

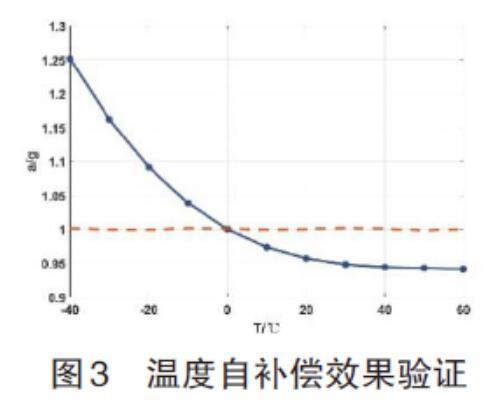
在MATLAB中，将两路频率值代入反解加速度的计算式，计算出各温度点下的补偿后加速度并记录变化趋势。如图3所示，虚线为补偿后，实线为补偿前。根据加速度计输出频率与输出加速度的理论关系公式计算未补偿时的加速度值，并与补偿后的加速度进行对比。结果表明：加速度漂移从补偿前的2997.1ppm/℃降低到49.9ppm/℃。

由此得出结论：通过该方法补偿后的加速度误差为补偿前1.66%，能够对加速度进行直接补偿，温度误差抑制效果较好。

4 结语

本文从硅微谐振式加速度计的输出频率特性入手，分析其工作原理，建立输出频率关于温度和加速度的二元方程组模型。通过对加速度计进行温度实验，分析频率温度特性，标定比例因子，分别得到了频率温度项和加速度项的系数，完成了模型的建立过程。通过反拟合的方法求解实际加速度值，并在此基础上提出了FPGA硬件实现方案，通过多周期同步测频法采集两路频率信号后，调用FPGA内部资源进行计算，可以得到实际的加速度值。通过实验验证温度自补偿方法的可行性，补偿后的加速度误差是补偿前的1.66%，实现了对加速度的直接补偿，温度误差抑制效果较好，说明通过该方法能达到高精度温度自补偿的目的。

参考文献

汪政，熊兴崟，李志天，等.谐振式加速度计动态特性研究[J].传感器与微系统，2020，39（6）：8-11.

Wang X ， Xu W ， Izhar， et al. Theoretical and Experimental Study and Compensation for Temperature Drifts of Micro Thermal Convective Accelerometer[J]. Journal of Microelectromechanical Systems， 2020， PP（99）：1-8.

李亨. 基于温敏结构的硅微谐振式加速度计温度补偿技术研究[D]. 东南大学， 2016.

庞作超. 硅微加速度计温度补偿技术研究[D]. 苏州大学， 2018.

张晶.硅微谐振式加速度计温度耦合非线性问题研究与敏感结构的优化设计[D].江苏：南京理工大学，2018.

於陈程， 张俊辉， 李永亮，等. 硅微谐振式加速度计温度效应标定与补偿[J]. 微纳电子技术， 2020， v.57;No.517（06）：60-66+81.

中图分类号：TH824.4 DOI：10.16660/j.cnki.1674-098x.2104-5640-6234 基金项目：2018YFB2002300（国家重点研发计划）。 第一作者：刘泽畅，（1996—），女，硕士在读，学生，研究方向为MEMS加速度计 通讯作者：邹旭东，（1986—），男，博士，研究员（Z），研究方向为谐振式加速度计

作者简介：

（第一作者）刘泽畅（1996——），女，硕士研究生，研究方向为MEMS加速度计。

基金项目：

国家重点研发计划（2018YFB2002300）