基于改进快速搜索和发现密度峰值算法的男童体型分类及判别
周 捷, 毛 倩
(西安工程大学 服装与艺术设计学院, 陕西 西安 710048)
中国儿童肥胖人群的增加导致儿童体型特征产生较大的变化[1],这就要求研究人员对儿童体型重新做出分析。一些学者主要就儿童体型发育规律和特点[2-3]、儿童参数化体型数据库[4-6]、以及儿童体型的判别归类[7-9]等进行了研究,但是,关于学龄男童体型分类判别方面的研究相对较少。相较于女童,男童更容易肥胖[10],对其体型的分析与分类尤为重要,科学的体型分类可以改善男童服装规格设计与适体性[11],并优化其体型判别。
人体体型拥有多维度特征[12-13],其数据集分布形态多样,需要选择一个合理的算法对其进行分类。研究表明快速搜索和发现密度峰值(CFSFDP)算法是一种基于密度的聚类算法,适用于各种类型的数据集且鲁棒性较好[14-15]。由于该算法中样本点的密度可以基于样本点之间的距离得到,且不同人体特征在距离计算过程中所占权重具有差异性,因此,本文引入灰关联度计算8个人体特征的权重,进而得到样本间的加权欧式距离,并基于此进行样本的加权聚类分析。
极限学习机(ELM)是一种学习速度快,泛化性能良好的机器学习方法,被广泛应用于多领域的分类识别[16]。本文为检验改进CFSFDP算法对体型判别的有效性,建立ELM男童体型判别模型,计算并对比CFSFDP聚类结果、加权CFSFDP聚类结果的判别正确率,以期通过提高分类算法的有效性来增加男童体型的判别准确率,为童装号型的推荐提供参考。
1 实验部分
1.1 数据采集
1.1.1 测量方法与对象
用接触式手工测量方式,采集了西安地区520位儿童身体尺寸数据。测量对象为身高(135.98±10.12) cm,体重(29.83±6.47) kg,年龄7~10岁的男童。
1.1.2 测量部位和要求
测量对象穿着统一的贴身内衣,测量时呼吸自然,测量环境为温度(22~25) ℃,相对湿度40%~60%的无风室内,以确保人体舒适。专业测量人员基于GB/T 16160—2017《服装用人体测量的尺寸定义与方法》的测量方法,根据GB/T 1335.3—2009《服装号型 儿童》和服装企业归号及制版的需求,采用单人单项测量方法,对被测试者的身高(F1)、胸围(F2)、总肩宽(F3)、腰围(F4)、臂长(F5)、臀围(F6)、腰围高(F7)和坐姿颈椎点高(F8)等8个人体特征进行了数据采集。
1.2 数据预处理
通过对测量数据进行缺失值替换、奇异值剔除、正态分布检验与相关性分析,得到有效样本435个。按加权CFSFDP算法样本计算量的要求,本文从7、8、9和10岁这4个年龄的有效样本中分别随机选取30个样本,以确保样本的合理分布与代表性,最终确定120个研究样本。
1.3 体型分类与判别模型
体型分类科学与否直接影响极限学习机模型对体型的判别精确性。本文采用灰关联度来量化男童人体特征的权重,提高CFSFDP算法对男童体型分类结果的科学性,为ELM体型判别模型提供优良的样本数据。
1.3.1 加权CFSFDP体型分类
CFSFDP算法根据数据点的局部密度ρ与距离δ找出类簇中心,并将剩余的数据点归属到密度比它们高的最近邻所属类簇,从而得到聚类结果。然而,数据点的局部密度与距离都以样本间的距离为计算基础[14],因此,本文首先采用灰关联度来计算男童人体特征的权重,其计算过程如下:
1)根据文献[17]计算人体第i个特征Fi(i=1,2,…,8)与第n个特征Fn(n=1,2,…,8,n≠i)之间的灰关联度rin;



最后,基于加权欧式距离dmq进行CFSFDP男童体型聚类分析。
1.3.2 ELM体型判别模型
ELM是由Huang等[18-19]提出的一种单隐层前馈神经网络,该算法可随机产生输入层以及隐含层间的连接权值和隐含层神经元的阈值,在训练过程中只需要设置隐含层的神经元的个数与激活函数,便可以获得最优解。与传统的训练方法相比,ELM极大提高了网络的泛化能力与学习速度[20-21]。本文基于ELM原理建立一种男童体型判别模型,其结构如图1所示。
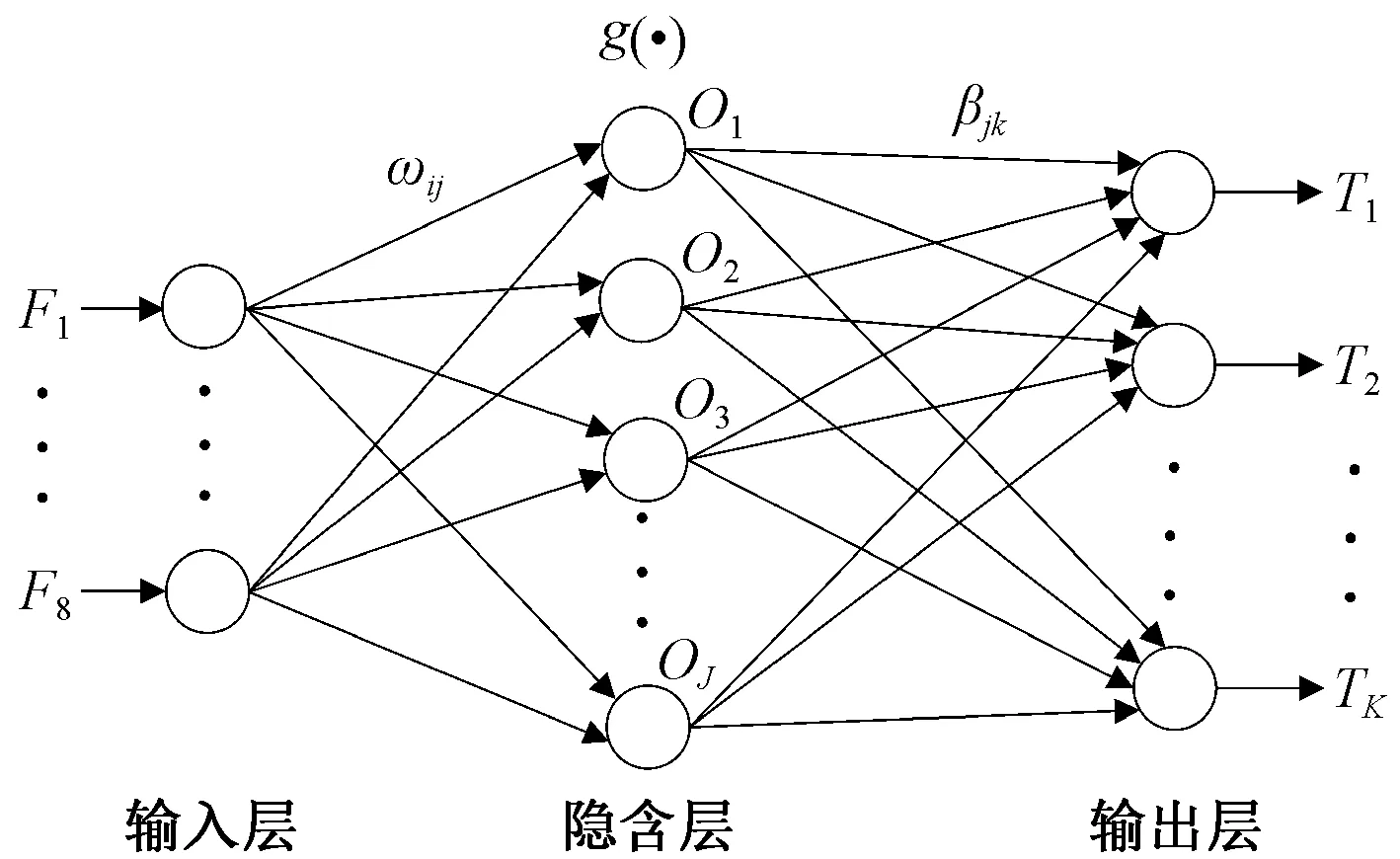
图1 ELM体型判别模型Fig.1 ELM model of body type recognition
基于加权CFSFDP算法对男童体型进行聚类,并应用ELM模型判别男童体型,分析加权CFSFDP算法对体型判别精确性的影响,从而验证该算法对体型分类判别的有效性,具体流程如图2所示。

图2 研究流程图Fig.2 Research process
2 结果与分析
2.1 特征权重分析
运用灰关联度对样本特征进行权重计算,得到8个人体特征权重,结果见表1。

表1 8个人体特征权重Tab.1 Eight feature weights for body type
由表1可知,关于男童人体特征,上身尺寸胸围、总肩宽所占权重较大,下身尺寸臀围的权重偏小,说明男童的体型主要取决于上身尺寸。
2.2 体型聚类分析

120个样本点关于(ρ,δ)的决策图如图3所示。选取局部密度ρ与距离δ都相对较大的点作为类簇中心,共4个。4类类簇中心的人体特征信息见表2。

图3 加权CFSFDP算法聚类决策图Fig.3 Decision diagram of weighted CFSFDP cluster

表2 4类类簇中心的特征Tab.2 Features of four class cluster centers cm
将剩余的每个样本点归属到局部密度ρ比它高的最近邻所属类簇中,并将样本数据映射到X-Y二维空间中,得到4类男童体型的样本数据集分布形状,如图4所示。由于类簇2、3、4的特征值呈现一定的递增规律,为研究其具体变化形式,计算3类类簇中心的特征差值,结果见表3。
在X-Y二维空间中,可以直观地观察样本类簇形状以及数据分布集散程度。加权CFSFDP算法得到的4类类簇分布边界分明,无相互交叉现象,表明该算法可以有效区分不同类簇的男童特征;类簇1的样本分布较为集中,类簇2的样本分布相对离散,类簇3的样本分布相对集中,类簇4的样本分布较为离散。
王国维在《论教育之宗旨》中说:“完全之人物不可不备真善美之德,欲达此理想,于是教育之事起,教育之事亦分三部,智育、德育、美育是也。”[5]341基于此,笔者认为当下哈萨克小说的创作,尤其是人文教育理念的凸显值得我们去思考并践行。

图4 样本数据二维分布图Fig.4 Two-dimensional distribution of sample data
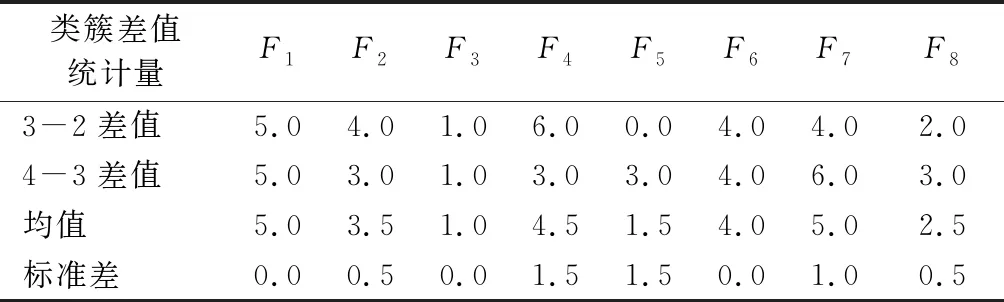
表3 类簇中心的特征差值Tab.3 Difference of features about cluster centers cm
在表3中,关于类簇2与3、类簇3与4之间的特征差值,F1、F3、F6的数值相等,F2、F7、F8的数值相差较小,F4,F5的数值相差较大。因此,类簇2、3、4的特征F1、F2、F3、F6、F7、F8近似呈公差为[5.0,3.5,1.0,4.0,5.0,2.5]的等差数列变化,F4与F5的规律性则较差,无明显变化规则。
计算4类男童类簇样本的特征均值,其结果见表4。

表4 4类类簇的特征均值Tab.4 Mean of features of four class clusters cm
比较表2与表4,计算类簇中心特征值与类簇特征均值的差值绝对值范围,类簇1到4分别为[0,1]、[0,4]、[1,3]和[0,5] cm。差值范围越大,表明类簇的样本分布越离散。类簇1的差值范围1 cm最小,说明该类簇的样本分布较为集中,聚类效果较好,且类簇中心代表性较强;类簇3的差值范围2 cm相对较小,表明该类簇的样本分布相对集中,其类簇中心可以代表该类簇体型;类簇2与4的差值范围4 cm和5 cm相对较大,说明其样本分布较为离散,这2类类簇的聚类效果偏差。上述分析与图4的样本数据集分布特征相一致,说明加权CFSFDP算法对男童体型的分类结果有较好的描述性与解释性。
统计4类类簇样本的男童年龄分布,结果如图5所示。
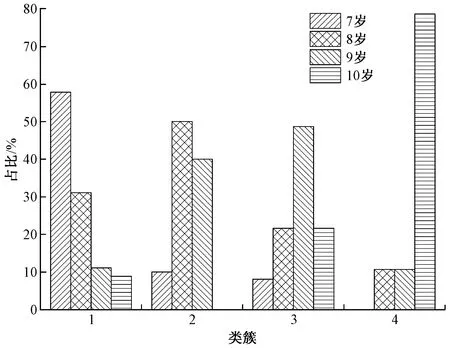
图5 聚类样本的年龄分布Fig.5 Age distribution of cluster samples
基于图4、5所示结果可知,男童体型共聚类得到4类类簇,每一类簇代表1种体型。由图4可知,类簇1也就是体型1的样本数最大,占总样本的37.50%,其中7岁男童的占比最高,8岁男童的占比其次,这一体型的身高、胸围等8个人体特征都较小,可定义为幼小型。对于类簇2也就是体型2,其样本数最小,仅为8.33%,儿童年龄范围为7~9岁,说明该体型的儿童属于特殊体型,缺少普遍性。由于其与体型1只有身高这一特征相差较大,其余7种特征都较为接近,故将其定义为瘦长型。在类簇3也就是体型3中,9岁的男童占比最大为48.65%,8岁与10岁的男童占比其次,其胸围与腰围等横向围度尺寸比体型2大较多,可定义其为中等型。就类簇4也就是体型4而言,10岁男童占比最大为78.57%;根据表3可知,体型2、3、4的类簇中心特征值,近似呈公差为[5.0,3.5,1.0,-,-,4.0,5.0,2.5]的等差数列变化,其中“-”表示不符合等差数列,因此可定义其为高大型。
基于以上分析,4类体型可对应为幼小型,瘦长型,中等型以及高大型,后3种体型的特征值近似呈等差递增趋势;7~8岁男童的体型主要为幼小型,9岁男童的体型主要为中等型,10岁男童的体型主要为高大型,体型的横向、纵向尺寸都随着年龄的增长而增加,其中纵向尺寸的增长速度偏快,各人体特征近似呈等差增加,男童无明显增肥趋势;幼小型与中等型的男童样本分布相对集中,瘦长型与高大型则较为离散,说明7~9岁男童的体型较为均匀,而10岁男童的体型则开始存在差异性,服装公司在设计制作男童服装时应考虑到这一变化,建议增加尺码的选择性并优化服装的结构设计,从而适应男童体型的多样性,提高童装适体性与舒适性。
2.3 体型判别与验证
为验证加权CFSFDP算法在男童体型判别中的优劣性,建立并训练ELM男童体型判别模型,调整神经元个数与激活函数,使模型达到相对优化状态,其中训练集样本为90个,测试集样本为30个。运行ELM模型判别测试集的体型类别,并与样本真实类别进行对比,结果如图6所示。

图6 体型判别准确率Fig.6 Accuracy of type recognition. (a) Clustering by CFSFDP; (b) Weighted clustering by CFSFDP
由图6可知,对于CFSFDP聚类结果,测试样本为30个,ELM判别正确21个样本,即准确率为70%;对于加权CFSFDP聚类结果,测试样本为30个,ELM判别正确27个样本,即准确率为90%,其中幼小型、中等型和高大型的判别准确率分别为100%、100%和60%,侧面验证了高大型的体型差异较大。对比2种聚类算法的判别准确率可知,加权CFSFDP算法可以有效提高体型判别准确率。
计算模型的判别准确率A,并输出模型神经元个数对2种体型判别模型的影响趋势图,如图7所示。
式中:A表示ELM男童体型判别模型的判别正确率;P表示类型判别正确的样本数;N表示测试集总样本数。

图7 隐含层神经元个数对ELM性能的影响Fig.7 Influence of number of hidden layer neurons on ELM performance
由图7可知,对比2种算法的隐含层神经元个数对ELM判别模型性能的影响趋势折线,CFSFDP算法的折线波动性更大,加权CFSFDP算法的折线相对稳定,说明对于男童体型判别,基于加权CFSFDP算法的ELM体型判别模型有更高的判别准确率与更好的鲁棒性。
3 讨 论
男童的体型分类与判别对儿童服装生产与号型推荐意义重大,较为科学准确的体型分类可提高极限学习机的体型判别精确性。基于此,本文提出一种加权CFSFDP算法,对男童体型进行分类。研究发现该算法可有效解释分类结果,并提高男童体型的极限学习机判别准确率。
本文将男童体型分为幼小型、瘦长型、中等型与高大型4种,这4种体型的特征值与年龄呈正相关,因此7~10岁男童的服装可考虑添加年龄为服装号型选择指标。除此之外,虽然本文发现男童上身特征在体型分类中占较大权重,但相关研究[11]表明随着年龄的增长,儿童下肢的生长速度要高于上体,故男童服装的长度参数要考虑到这一变化,随着号型的增大,下装的长度增加量要偏高于上装。与同年龄段的女童相比,男童的体型变化主要在纵向长度尺寸上,而女童体型则开始横向维度尺寸的变化[9],因此童装结构制版与儿童号型中应该对7岁以后的男童、女童进行区分,以适应其不同的发育特点,提高服装的合体性。本文发现男童体型从10岁开始呈现多样性,其人体特征出现不均衡发展,在日后的研究中,需要对该年龄段男童进行体型细分,为童装企业的结构制版及服装号型设置提供参考。由于样本容量与地域性的限制,本文研究对象中并未出现过度肥胖体型男童,但为了提高研究结果的普适性,在以后的男童体型研究中,需要扩大样本年龄及地域范围。
虽然加权CFSFDP算法可以提高ELM模型关于体型判别的鲁棒性与准确率,但其准确率仍偏低。一方面可能是因为训练样本偏少,另一方面判别错误的体型主要是高大型,该体型的特征离散性较大,若进一步细分该体型并扩大样本数,可以改善男童体型判别结果。
4 结 论
本文采用灰关联度来量化男童人体特征权重,实现基于加权CFSFDP算法的男童体型分类与判别,得到如下主要结论:
1)相比于快速搜索和发现密度峰值(CFSFDP)算法,加权CFSFDP算法对于ELM体型判别模型有更好的鲁棒性,并有效提高男童体型判别的准确率。
2)7~10岁西安地区男童的体型可以分为幼小型、瘦长型、中等型、高大型4类;其中7~9岁男童的人体特征值与年龄呈正比增长关系且近似为等差序列,10岁的男童体型开始出现多样化。

