GPS滑坡位移监测时序分析与组合建模预测

罗袆沅，蒋亚楠,，许 强，唐 斌

(1.成都理工大学 地球科学学院,四川 成都 610059；2.成都理工大学 地质 灾害防治与地质环境保护国家重点实验室,四川 成都 610059)

0 引言

GPS的静态观测作为滑坡变形监测的常用方法，其变形监测数据是滑坡预警预报的重要依据，在滑坡实时监测过程中起指导作用[1-2]。基于变形监测数据建立有效的预测模型，不仅能减少监测工作量与成本，同时又能降低变形发育致灾发生的机率。

滑坡作为一种常见的地质灾害，通常由多种不确定因素，如地质条件、地貌、水文地质和物理因素以及人类活动等共同作用导致。因此，需结合多种监测手段对滑坡变形状态进行定量分析。而滑坡变形预测一直是滑坡预警预报的重要研究方向和研究热点[3-4]。由于滑坡变形演化受季节性因素(如库水位调度、周期性强降雨)影响，滑坡累积位移曲线通常表现出很强的非线性动力学特征，如阶跃性变化等。常规方法对此类滑坡进行预测预报时，极易将阶跃性的变形特征误认为滑坡已进入临滑阶段，造成误判[5]。因此传统的分析方法很难对滑坡的稳定性做出准确评价。在分析此类滑坡时，需充分考虑滑坡位移与其外部影响因素间的关系，只有在深入研究两者的响应关系的基础上才能准确地实现滑坡的预测预报[6]。

由于滑坡累积位移时序包含滑坡内部影响因素(地质结构、地形地貌)加持的趋势部分，以及外部影响因素(降雨、库水位变化)波动的周期部分，将位移时序分解为趋势项和周期项并分别建模预测变得尤为重要。支持向量回归机(Support Vector Regression, SVR)模型是基于统计学习理论所建立[7]，目前已广泛用于此类滑坡的周期项位移预测。然而，其预测性能易受模型参数选择的影响，过去通常采用多种参数寻优法解决这一问题[8-11]，并未考虑影响因子之间的线性关系，造成样本数据冗余；同时趋势项位移预测多采用多项式拟合的方法，容易造成拟合结果不稳定、收敛效果差。因此，本文通过采用核主成分分析(Kernel Principal Components Analysis, KPCA)实现影响因子的特征提取[12]，消除影响因子间的相关性，提高影响因子的质量，降低样本数据冗余；并通过二次指数平滑(second exponential smoothing, DES)拟合趋势项位移[13]，以消除多项式拟合结果的不稳定性。相对于网格搜索算法(Grid Search, GS)[14-15]、遗传算法(Genetic Algorithm, GA)[16-17]，粒子群(Particle Swarm Optimization, PSO)寻优算法[18-20]结构较为简单，且寻优性能更胜一筹。因此，建立结合PSO算法确定SVR模型参数的最优组合模型。以三峡库区白水河滑坡为分析对象，在KPCA特征分析的基础上，建立PSO-SVR联合DES的组合预测模型实现滑坡位移预测分析。

1 模型原理

1.1 时间序列数据预处理

通常时间序列是由3部分组成(趋势项、周期项和随机项)[21]。在滑坡位移的监测数据中，趋势项是受滑坡体内部因素(地质结构、地形地貌)影响的线性部分，周期项是受滑坡区域环境的外部因素(降雨、库水位波动)影响的非线性部分，而随机项是随机噪声。因此，时间序列组成公式如下：

D=Dp+Dt+Dr

(1)

式中，D为总位移，Dp为周期项位移，Dt为趋势项位移，Dr为随机项位移。

本文采用小波去噪方法去除监测数据中的随机噪声项。Hodrick-Prescott(HP)滤波器是Whittaker于1923年首次提出的[22]，这种方法被广泛应用于宏观经济的趋势分析研究。该方法采用对称的数据移动平均方法的原理，将时间序列中具有一定趋势变化的平滑序列(趋势项)分离出来，然后原序列减去趋势项得到周期项。得到趋势项的公式如下：

(γt-1-γt-2)]2}

(2)

式中yt为时间序列，λ为平滑参数，γ为趋势分量。在本研究中，滑坡位移每年急剧增加一次，因此，平滑参数λ的值被确定为100。

1.2 核主成分分析

为了更好地处理非线性数据，引入了非线性映射函数φ，将原空间的数据映射到高维空间中[12]，本文将滑坡影响因子序列xt映射到φ(xt)中，核主成分分析(kernel principal components analysis, KPCA)求解特征值如下：

(3)

(4)

(5)

1.3 二次指数平滑

指数平滑法是一种特殊的加权移动平均法，其特点是最新数据的权重高于早期数据，此权重的因子随着数据的老化依指数下降。二次指数平滑是指数平滑的衍生，它更适用于具有一定趋势的时间序列的预测[13]。所以，本文采用DES拟合趋势项位移。

对于一组时间序列{xi}，{si}代表第i时刻的指数平滑值，{bi}代表第i时刻的趋势最佳估计。DES的预测值为Fi+m，代表第i次后的m次预测，通常m=1。DES算法的公式如下：

Fi+m=si+mbi

(6)

si=ζxi+(1-ζ)(si-1+bi-1)

(7)

bi=ξ(si-si-1)+(1-ξ)bi-1

(8)

式中，s1=x1，b1=x1-x0，ζ为数据平滑因子(0<ζ<1)，ξ为趋势平滑因子(0<ξ<1)。

1.4 粒子群优化

此算法在寻优过程中，核心步骤是更新种群中每个粒子的位置和速度，而速度的更新最为关键。文献[18-20]详细说明了粒子群寻优算法的寻优原理。速度更新公式为：

vi=ω×vi+c1×rand()×(pbesti-xi)+

c2×rand()×(gbesti-xi)

(9)

式中，vi是粒子的当前速度，w为惯性因子，rand()是随机生成函数，生成值在(0-1) 之间，pbesti和gbesti分别为历史最优位和当前最优位，c1和c2为学习因子，通常c1=c2=2。位置更新的公式如下：

xi=xi+vi

(10)

1.5 支持向量回归机

支持向量机(support vector machine，SVM)是一类按监督学习方式对数据进行二元分类的广义线性分类器，最大边距超平面是其决策边界对学习样本的求解[8-11]。它成功地解决了BP神经网络的过学习现象及局部最小问题，并在小样本训练中体现出优异的性能。因此，本文采用SVR模型对滑坡周期项位移进行预测。

在非线性的变换之后，支持向量机使输入的向量映射到高维特征空间中。通过构造最佳的决策函数，将原有空间的核函数来替换高维特征空间中的点积运算。应用有限的样本学习训练以获得全局最优值。SVR估计函数为:

f(x)=WTφ(x)+b

(11)

将估计函数通过ε不敏感损失函数转化为优化问题，SVR回归预测模型可以通过二次规划算法获得：

(12)

2 滑坡变形特征分析

2.1 白水河滑坡GPS监测点布设

根据白水河滑坡的地形、地质条件、变形特征、观测通视情况，确定该滑坡的监测内容主要为地表位移监测、钻孔测斜监测、地下水位监测等。监测初期布设的7个GPS监测点分布在3条纵向剖面上(图1)，中间剖面有3个GPS监测点(ZG118、ZG119、ZG120)，两侧剖面分别布设2个GPS监测点(ZG91、ZG92、ZG93、ZG94)。2004年7月，由于白水河滑坡变形的突变产生较大的裂缝，经专家评估建立了滑坡预警区，而后在预警区内先后增建了4个GPS监测点(XD-01、XD-02、XD-03、XD-04)，在滑体外围东西两侧基岩脊上各建立1个GPS基准点。滑坡区内共11个GPS变形监测点，均采用美国产天宝GPS接收机(平面精度5+1ppm)进行滑坡地表位移变形监测。以上监测自2003年6月上中旬三峡大坝坝前水位蓄水至135m开始获得起始数据，以后每月监测一次。其中，位于滑坡位移活跃区内的监测点有ZG93、ZG118和XD-01、XD-02、XD-03、XD-04。

图1 白水河滑坡GPS监测点Fig.1 Layout of GPS monitoring points of Baishuihe Landslide

2.2 滑坡体地质工程特征

白水河滑坡位于三峡大坝以西约56km处，是三峡水库重要的滑坡监测区域。白水河滑坡为深层大型土质滑坡，处于长江南岸单斜顺层斜坡，该结构单元位于白福坪背斜北翼，属于侵蚀堆积谷的低山丘陵地貌。滑坡的平面形态为不规则矩形，左右宽度约450m，长度约352m，面积约16×104m2，体积约550万m3，变形体的平均厚度约为35m，主滑方向为NNE20°。如图2所示，滑坡面为基岩与残坡积层的接触带，厚度约为0.9～3.1m，呈折线形；滑坡体的基岩性为中厚岩砂夹薄层泥岩，产状15°∠36°，岩层中节理裂隙发育[23]；滑坡体主要由第四系残坡积碎石土组成，碎石含量20%～40%。

2.3 滑坡体变形特征

白水河滑坡属于古滑坡堆积体，自2003年6月三峡水库蓄水以来，滑坡开始复活，变形逐渐加剧。专业监测数据显示，白水河滑坡从2005年6月开始，发生了几次严重的宏观变形。其中，2007年出现了监测以来最剧烈的一次宏观变形；2008—2014年，变形逐渐趋于平缓，在强降雨的作用下，滑坡局部出现了浅层坍塌，但其宏观变形迹象未出现明显的变化。

图2 滑坡工程地质剖面Fig.2 Engineering geological section of landslide

图3 白水河滑坡累积位移-库水位-月降雨量-时间关系Fig.3 Cumulative displacement-reservoir water level-monthly rainfall-time diagram of Baishuihe Landslide

自2003年7月布设专业监测以来，白水河滑坡监测点的变形呈现阶跃性特征(图3)。结合图1分析，预警区内监测点在每年5～9月，滑坡变形整体增大，10月到次年4月趋于平缓，说明库水位涨落和降雨叠加作用对滑坡的稳定性有较显著的影响。每年5～9月份为三峡库区的雨季，在此期间，该区降雨持续时间久、强度大，滑坡受季节性降雨的影响，表现出阶跃性的变化特性，其中6～7月滑坡位移变化最为明显，特别在2007、2008和2009年受强降雨的影响，出现非常明显的位移剧增现象。每年5月开始，降雨急速增加，三峡水库为防止洪灾开始放水，水库水位明显下降，因此水库水位与降雨量呈负相关的关系。当降雨量增加且水库水位显著下降时，往往伴随着滑坡位移量的急剧变化，如2007年6月滑坡前缘受库水作用强烈，监测点XD-01、XD-03累积位移增长明显高于中西部监测点XD-02、XD-04、ZG93和ZG118，进一步说明了滑坡体东北部结构的不稳定性。相比之下，非预警区监测点多年变化较小且呈直线型。

通过上述分析可知，如果水库水位下降期间伴随强降雨作用，会对滑坡的稳定性产生更不利的影响。因此，本文以活跃区内典型位移监测点ZG118为代表，结果同期的降雨量和库水位高程对其滑坡位移时序进行分析预测。

3 滑坡位移预测

3.1 位移预测技术路线

通过分析，本文以2003年7月至2013年2月的GPS滑坡位移监测数据为分析对象，综合考虑库水位、降雨量对滑坡位移的影响，构建滑坡位移组合优化动态预测模型，处理流程如图4所示。

图4 预测流程图Fig.4 Forecast flow chart

(1)对位移监测时间序列和初始影响因子进行预处理，采用小波去噪方法去随机噪声，并进行归一化处理。

(2)利用HP滤波器将位移监测时间序列分解为周期项位移和趋势项位移。

(3)现有三峡库区内滑坡失稳的持续形变都与库水位涨落及降雨导致地下水渗流场改变有关，库水位和降雨与位移变化的相关性强。杨背背[23]、Chao[24]等分析了变形影响因素的滞后性，择取单期或多期库水位和降雨数据作分析及模型输入。因此，综合考虑库水位、降雨量的滞后影响，选择每月库水位、每月库水位变化幅值、每月库水位变化速率、每月降雨量和前两月累积降雨量5个变量，构建滑坡周期项位移的动态响应模型。

(4)对原始位移监测数据与初始影响因素变量进行核主成分分析，结果见表1。第一二主成分对原始数据的累积方差贡献率达到82.37%，表明2个主成分包含了原始数据的大部分信息。因此选取这2个主成分作为新影响因子建立预测模型。

表 1 解释的总方差

(5)趋势项位移预测：选取2003年7月到2010年8月的86组白水河滑坡专业监测点ZG118的观测数据为训练样本，并以2010年9月到2013年2月的30组数为测试样本，利用MATLAB编程实现DES预测模型，数据平滑因子ζ为0.99，趋势平滑因子ξ为0.98，模型预测结果如图5所示。

(6)周期项位移预测：预测模型的样本选取同上，使用MATLAB编程实现PSO参数寻优，得到SVR径向基核函数参数γ=0.65938，C=2.1656。根据最优模型参数，学习训练样本数据，构建滑坡周期项位移与影响因子间的动态响应模型，同时对滑坡的周期项位移进行预测，并通过测试样本评估模型的预测精度和泛化性。

(7)将DES趋势项预测结果和PSO-SVR周期项预测值通过加法模型，得到滑坡总累积位移结果，如图7所示。

图5 DES趋势项预测结果Fig.5 Forecast results of trend items of DES

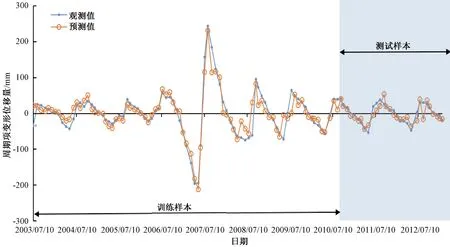
图6 PSO-SVR周期项预测结果Fig.6 Forecast results of periodic items of PSO-SVR

图7 滑坡累积位移预测结果Fig.7 Prediction results of the cumulative displacement of landslide

3.2 预测结果分析

为进一步对比分析本文算法的优越性，在同样完成主成分分析处理后，使用3种不同的优化算法来搜索SVR的模型参数，并建立相应的响应模型预测滑坡周期项位移。计算预测模型结果的均方根误差(RMSE)、平均绝对百分比误差(MAPE)、相关系数(R2)。

(13)

(14)

(15)

由表2可见，在相加了趋势项位移的累积预测结果后，相较于基于网格搜索寻优支持向量回归机(GS-SVR)和遗传算法寻优支持向量回归机(GA-SVR)的预测，粒子群寻优支持向量回归机(PSO-SVR)结果的RMSE和MAPE均为最小，而且R2最大，R2为0.89801，表明预测值与观测值具有极强的相关性，即PSO-SVR模型在经过KPCA分析后是最佳预测模型，并且该方法在分析影响因子对滑坡位移的变形影响作用中，具有极好的预测及泛化能力。从而证实了在参数优化算法中，PSO算法对白水河滑坡预测的参数优化明显优于传统的网格搜索法和遗传算法。同时，由于DES兼容了全期平均和移动平均所长，通过定权的方式决定观测数据的贡献量，不舍弃过去的数据，使得其预测结果的收敛性明显优于多项式拟合。综合以上分析可知，本文所提出的滑坡组合优化预测模型具有很好的预测能力，滑坡位移预测效果可靠性高。

表 2 不同模型的累积位移预测误差

4 结论

本文在综合分析白水河滑坡GPS实时监测位移及同时期降雨量、库水位的监测数据的基础上，得出在降雨量和库水位变化2个外部因子共同作用下影响滑坡的变形特征。考虑到二者对滑坡作用具有滞后性，选取每月库水位、每月库水位变化幅值、每月库水位变化速率、每月降雨量和前两月累积降雨量5个变量作为分析的初始影响因子。据此，提出PSO-SVR联合DES的滑坡位移预测优化模型实现白水河滑坡的位移预测。首先，在对位移监测时间序列进行小波去噪处理的基础上，利用HP滤波器将其分解为受地质条件长期控制的趋势项和受季节性因素影响的周期项，并通过核主成分分析将初始影响因子重构为两个主成分分量，用于SVR模型的构建。模型构建过程中，采用PSO算法寻优SVR模型参数，学习训练样本数据，对周期项位移进行预测；并采用DES模型对趋势项位移进行预测。最后，将两模型的预测值相加得到最终预测值，并通过与测试样本序列对比分析进行预测结果的精度评定。评定结果显示，本文提出的组合优化预测模型预测结果的RMSE为18.2031mm，R2为0.89801，明显优于基于网格搜索寻优支持向量回归机(GS-SVR)和遗传算法寻优支持向量回归机(GA-SVR)模型预测结果，证实了该模型的预测能力和可靠性。