薄透镜成像位置的测定方法研究

彭强 沈雪飞 杨英

摘   要：针对薄透镜成虚像和虚物成实像的测量方法，提出两种方案：一是利用实物成虚像法测量虚像像距，具有一定的创新性;二是利用虚物成实像法测量虚物物距，并结合中学物理薄透镜成像规律进行分析和比较。该实验研究拓展了凸透镜成虚像的规律，为确定凹透镜虚物位置开拓了实验思路，也为一线教师讲授薄透镜相关知识提供了实验参考。

关键词：薄透镜成像;虚像;实像;焦距

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2021）12-0042-4

在中学物理教学中，学生通过实验积累感性认识，经过教师引导进行科学推理，思维方法上升到理性认识，最终总结出凸透镜成像规律，从而定量理解凸透镜成像规律。关于凸透镜成实像的规律，要求学生知道物距、像距和焦距之间的定量关系;对凸透镜成虚像的规律，仅仅要求学生知道成正立、放大的虚像，像与物在透镜同侧，用眼睛直接观察虚像所处位置，并未对虚像像距进行定量研究。这主要源于所成虚像不是由真实光线形成，而是由光线的反向延长线形成的，因此只能被眼睛观察到，而不能被光屏直接接收，从而导致学生不能利用光屏接收虚像和确定虚像像距。对于凹透镜成像，教材中只涉及凹透镜是发散透镜，未进一步讨论凹透镜成像规律和凹透镜成像的相关问题。学生对这两个问题时常有疑问，而不知如何解决。教师若未认真思考以上问题，往往不能科学解答。再者，中学实验室中相关教具较为缺乏，缺少相关实验演示，导致出现让学生死记硬背的现象。

本文基于薄透镜成像的相关理论，分别从普通物理实验（光学部分）和中学物理实验两个角度，提出两种不同的方案：一是利用实物成虚像法测量虚像像距，二是利用虚物成实像法测量虚物物距。其中，方案一利用两个凸透镜来确定凸透镜的虚像像距，具有一定的创新性。即在光源1经凸透镜O1所成虚像的位置附近，利用另一个光源2来代替其虚像位置，通过调整凸透镜O2的位置，让光源1和光源2通过凸透镜所成的实像都能被光屏同时接收（图1、图2），最后适当移动凸透镜O2和光屏，当两实像在光屏上同时清晰或模糊时，说明光源2所处位置是光源1经凸透镜O1所成虚像的位置。方案二利用一个凸透镜和一个凹透镜来确定凹透镜的虚物物距，通过理论推导与实验验证，证实两种方案的可行性。

1    普通物理实验（光学部分）与中学物理处理薄透镜成像问题的对比

1.1    普通物理实验（光学部分）处理凸透镜成像问题

利用实物成虚像法测量凸透镜的虚像像距示意图如图1所示，该实验计算过程采用新笛卡尔符号法则，根据透镜成像的高斯公式[1]：

空气中的凸透镜焦距f′>0，凸透镜对实物成像时，物距s<0，由（1）式可知，如果像距s′>0，此时像为实像;如果像距s′<0，像为虚像，物与像位于同侧[2]。

对于凸透镜O1，应用薄透镜成像公式：

可计算出光源P1通过凸透镜O1所得虚像的像距，其中：

对于凸透镜O2，应用薄透镜成像公式：

可计算出光源P2通过凸透镜O2成像的物距，其中：

调整光源P2和凸透镜O2的位置，使光源P1和P2通过凸透镜同时在P3处成清晰的像，此时只要测出所测透镜的s1=-O1P1，s1′=-O1P2，s2=-O2P2以及s2′=O2P3，根据（2）（3）（4）和（5）式，即可计算和检验光源P1经凸透镜O1所成的虚像像距。

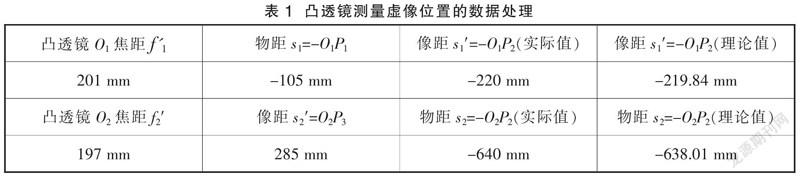
图2为图1相对应的实物图，图中P2为光源2（手机代替，屏幕显示倒立的顶角为30°的直角三角形的下半部分），P1为透明光源1（倒刻有顶角为30°的直角三角形的上半部分），O1为凸透镜1（只有下半部分的平凸镜，焦距f'1=201 mm），O2为凸透镜2（焦距f'2=197 mm），P3为光屏。固定P1、O1和O2在光具座的位置（分别为255 mm、360 mm和780 mm），调整光屏P3位置使其出现光源P1倒立清晰的影像。再打开光源P2，并调整其位置，也使其在光屏P3上出现清晰的像，记录此时光屏P3和光源P2的位置。最后，改变凸透镜O2的位置，调整光屏P3的位置使像再次清晰，这时可以发现光源P1、P2所成的像同时在光屏P3上清晰，且光源P1所成的像是正立的顶角为30°的直角三角形的上半部分，光源P2所成的像是正立的顶角为30°的直角三角形的下半部分，二者能够组成一个完整的顶角为30°的直角三角形（图3），说明光源P2所处位置就是光源P1经凸透镜O1所成虚像的位置。本实验的关键是使用透明发光体P1。实验数据处理如表1所示。

从表1中可看出，在误差允许的范围内，对于凸透镜O1，光源P1通过凸透镜O1所成虚像像距的理论值与实际值基本相等，说明虚像像距为-220 mm，即虚像在光具座的140 mm位置处。对于凸透镜O2，光源P2通过凸透镜O2所成像的实物物距的理论值与实际值也基本相等，说明实物物距为-640 mm，即实物位于光具座的140 mm位置处。综上所述，P2位置就是光源P1经凸透镜O1所成虚像的位置。

1.2    普通物理实验（光学部分）处理凹透镜成像问题

利用虚物成实像测量凹透镜的虚物物距示意图如图4所示，该实验计算过程采用新笛卡尔符号法则。

对于凸透镜O1，应用薄透镜成像公式：

可计算出光源P1通过凸透镜O1所得实像的像距，其中：

对于凹透镜O2，应用薄透镜成像公式：

可计算出虚物P2通过凹透镜O2所得虚物的物距，其中：

物距s2=O2P2，像距s2′=O2P'2（9）

因此，只要测出所测透镜的s1=-O1P1，s1′=O1P2， s2=O2P2以及s2′=O2P'2，根據（6）（7）（8）和（9）式，即可计算和检验所测凹透镜O2的虚物物距。

图5为图4相对应的实物图，图中P为光源，P1为物体，O1为辅助凸透镜（焦距f1= 204 mm），O2为凹透镜（焦距f2=-652 mm），P2为光屏。固定P、P1和O1在光具座的位置（分别为50 mm、200 mm和900 mm），调整光屏P2的位置使其出现光源P1的倒立清晰影像，记录P2的位置，再将凹透镜O2置于凸透镜O1和光屏P2之间的适当位置，将光屏P2向外移动，再次得到倒立清晰的像P2′（图6），记录P2′的位置[3]。对凹透镜O2来说，P2是虚物体，P2′是实像。本实验的关键是使用辅助凸透镜O1确定凹透镜虚物体的位置，数据处理如表2所示。

从表2中可看出，在误差允许的范围内，对于凸透镜O1，物体P1通过凸透镜O1所成实像像距的理论值与实际值基本相等，说明所成实像在光具座的1188 mm位置处。对于凹透镜O2，利用虚物体P2通过凹透镜O2所成实像及其像距倒推出虚物物距的理论值与实际值也基本相等，说明虚物物距为138 mm，即虚物位于光具座的1188 mm位置处。综上所述，P2位置就是凹透镜O2虚物成实像对应的虚物位置。

1.3    中学物理处理薄透镜成像问题

对于薄透镜成像有公式：

其中，u为物距，v为像距，f为凸透镜的焦距。

利用实物成虚像法测量凸透镜的虚像像距示意图如图7所示，由于光源P1经凸透镜O1所成像为虚像，故只能用眼睛观察虚像P1′，但无法确定其所处位置。光源P2经凸透镜O2所成实像的像距v=285 mm，物距u=640 mm，其中凸透镜O2的焦距f2=197 mm，数据处理如表3所示。

从表3中可看出，在误差允许的范围内，对于凸透镜O2，光源P2通过凸透镜O2所成像的实物物距的理论值与实际值基本相等，说明光源P2在光具座的140 mm位置处。光源P1、P2所成的像同时清晰呈现在光屏上，P2位置就是光源P1经凸透镜O1所成虚像的位置。

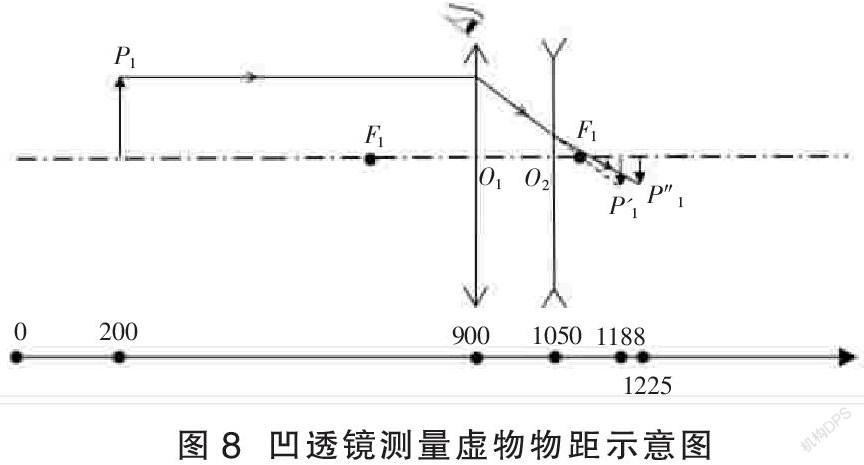
利用虚物成实像测量凹透镜的虚物物距示意图如图8所示，其中未加凹透镜O2时，实物P1经凸透镜O1所成实像的像距v=288 mm，物距u=700 mm，焦距f1=204 mm。对于凹透镜O2， P1′为虚物，故只能用眼睛观察虚物P1′，无法确定其所处位置，但其经过凹透镜O2所成实像P1″可被光屏接收，数据处理如表4所示。

从表4中可看出，在误差允许的范围内，对于凸透镜O1，實物P1通过凸透镜O1所成实像像距的理论值与实际值基本相等，说明P1′在光具座的1188 mm位置处。

2    结  论

通过对以上两个实验所得数据进行处理可得，利用实物成虚像法测量虚像像距的实验方案以及利用虚物成实像法测量虚物物距的实验方案都具有可行性。其中，利用实物成虚像法测量虚像像距的实验方案具有一定的创新性，巧妙地利用透明光源1、光源2（手机代替）、两个凸透镜（O1和O2）以及光屏，获得光源1所成的实像1，以及光源2所成的实像2，通过对两个实像的分析，测得比较难获得的光源1通过凸透镜O1所成的虚像像距。笔者建议中学物理教师可采用以上两种实验方法进行演示教学，让学生体会利用相关物理知识直观观察凸透镜的虚像以及测量虚像的位置。其次，让学生拓展关于凹透镜虚物成实像的知识，填补凹透镜成像的空白。从而使学生加深对虚物、虚像的理解，加深对透镜成虚像的理解，培养创新能力。

参考文献：

[1]姚启钧.光学教程[M].北京：高等教育出版社，2014：131-141.

[2]顾菊观，钱淑珍.凸透镜焦距测量方法的探索[J].大学物理实验，2014，27（01）：49-51.

[3]杨述武.普通物理实验3：光学部分[M].北京：高等教育出版社，2016：16-18.

（栏目编辑    刘   荣）