一次侧失谐参数对三线圈磁谐振无线电能传输系统的影响

钱培聪, 陆益民

(广西大学 电气工程学院， 广西 南宁 530004)

0 引言

磁谐振无线电能传输(Magnetic Resonance Wireless Power Transmission, MR-WPT)技术是无线电能传输技术中的一个热门研究方向[1-2]。MR-WPT因具有较远的传输距离和较高的传输效率而被广泛应用于工矿[3]、轨道交通[4]等领域。然而，由于线圈之间存在交叉耦合,会引起MR-WPT系统发生失谐现象，即此时一次侧的电压与电流不再保持同相位，造成逆变器无法实现软开关运行，带来较大的损耗，不利于系统获得较大的传输功率与传输效率[5-6]。为了解决上述问题，国内外专家学者进行了大量的研究。文献[7]提出了一种自适应阻抗匹配法，通过在一次侧采用串联和并联的电容阵列实现动态的阻抗匹配,以输出最大的功率，但该方法需要使用7个电容阵列，硬件电路部分过于繁琐。文献[8]提出了一种基于锁相环的频率跟踪法，通过一次侧的交流电压和交流电流保持同相位的方式来使系统稳定地处于谐振状态，达到最大化输出功率的效果，但该方法中的逆变器没有实现软开关，存在一定的损耗。文献[9]针对三线圈结构的MR-WPT系统提出了一种调频控制方法，即在传输距离不同时通过寻找最优的开关频率使系统获得更高的传输效率，取得了较好效果，传输效率提升了15%，但该方法的控制策略较为复杂，需要附加硬件电路和控制电路，实现难度较大。文献[10]应用Hame轨迹法分析了MR-WPT系统的自激振荡，并提出了一种用于一次侧调谐的延时迭代法，使得一次侧处于零电压开关状态，一次侧与二次侧之间不需通信联系,省去了部分硬件，然而该方法需在电源电压稳定的基础上展开，在实际应用中存在局限性。文献[11]采用动态的人工蜂群算法分析MR-WPT系统的失谐参数与传输功率之间的关系，该算法将整个求解空间中多个最大值的多峰函数优化搜索转换为在每个细分中搜索一个全局最大值，具有收敛速度快、优化精度高的优点，但该方法适用场合有限，只有在特定的失谐参数下才能实现。文献[12]采用一种模型预测方法对MR-WPT系统进行预测，研究了传输功率与失谐参数的关系，并通过仿真验证了该方法的失谐补偿效果,但该方法仅在软件仿真层面上进行了可行性验证,实际应用效果还有待进一步验证。文献[13]采用一次侧最小电流频率跟踪的调频方法，通过测量一次侧电流有效值与电源电流平均值并计算出两者的最小比值，实现实时调节开关频率的效果，但该方法需要复杂的控制策略，硬件与软件实现都有一定的难度。文献[14]针对MR-WPT系统提出了一种一次侧失谐参数补偿方式，得到了一种具有抗偏移的失谐拓扑结构，失谐补偿参数的设计不涉及复杂控制策略与附加硬件电路，可行性较强，但该方法所考虑的失谐参数变量较多，参数之间的关系较为复杂。

针对上述方法存在的问题，采用三线圈串联型磁谐振式失谐拓扑结构，提出了一种MR-WPT系统一次侧失谐参数设计方法，通过引入虚拟耦合因数简化参数计算过程，无需复杂的算法与设计额外的硬件电路，具有较强的可行性。研究了一次侧失谐参数对三线圈MR-WPT系统的影响，分析了MR-WPT系统3个线圈回路之间的不同虚拟耦合因数、失谐因子与系统传输功率的关系，实现了在不同的虚拟耦合因数、失谐因子条件下获得最大的输出功率。

1 三线圈MR-WPT系统分析

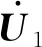
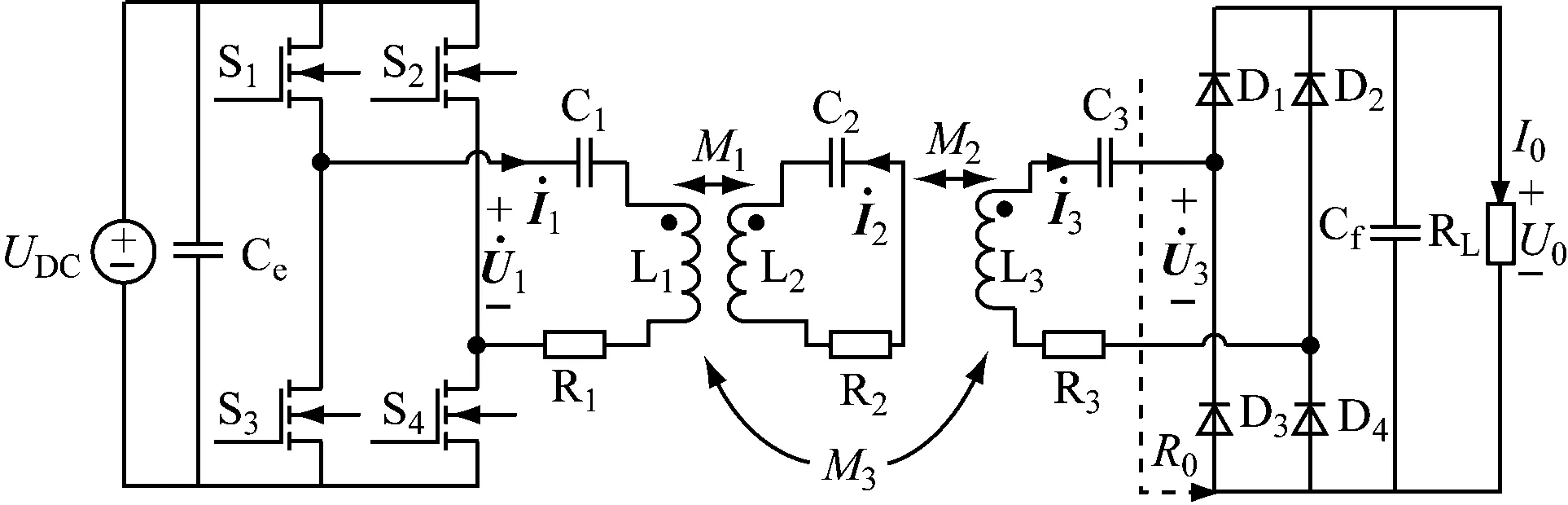
图1 三线圈串联MR-WPT系统主电路Fig.1 Main circuit of three-coil series MR-WPT system

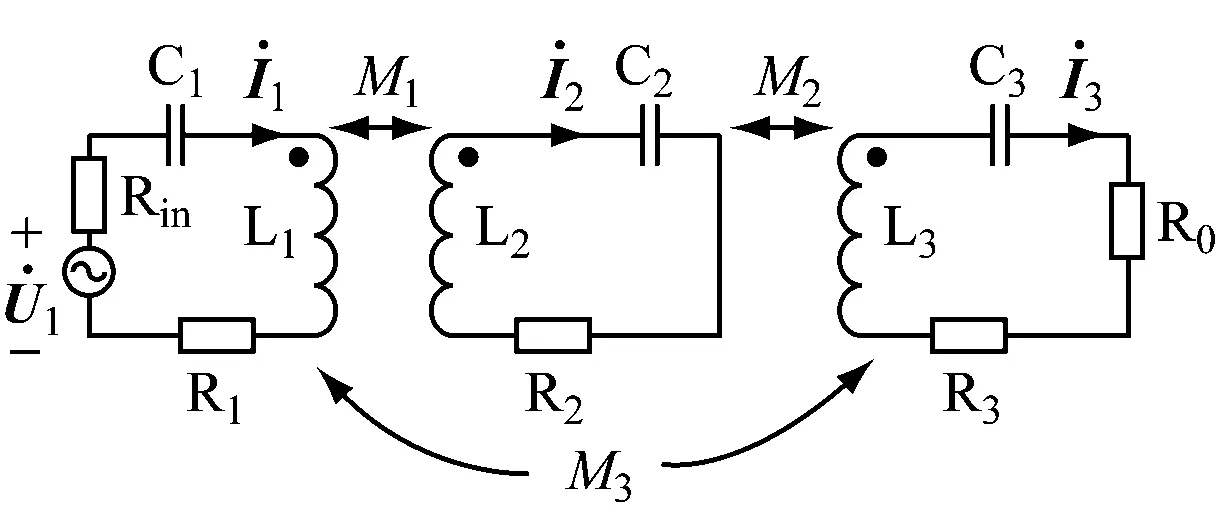
图2 简化电路Fig.2 Simplified circuit

根据图2，由基尔霍夫电压、电流定律可得

(1)

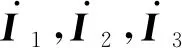
(2)

式中A=Z1Z2Z3+Z1(ωM2)2+Z2(ωM3)2+Z3(ωM1)2-2jωM1ωM2ωM3。

忽略整流损耗，根据式(1)、式(2)可得到输出功率P及传输效率η为[9]

(3)

(4)

式中I1,I2,I3分别为3个线圈回路电流的有效值。

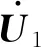
2 一次侧失谐参数设计与分析

一次侧失谐参数主要有线圈回路之间的内阻比、失谐因子、虚拟耦合因数、回路品质因数等[14-15]。为方便分析，图2中取R3+R0=R，L1=L2=L3=L，C1=C2=C3=C，定义λ1为发射线圈回路与中继线圈回路内阻比，λ1=(R1+Rin)/R；定义λ2为发射线圈回路与接收线圈回路内阻比，λ2=R2/R；定义λ为负载比，λ=R0/R；Qi(i=1，2，3)为对应3个线圈回路的品质因数，Q3=ω0L/R=Q，Q1=Q/λ1，Q2=Q/λ2，ω0为电路谐振角频率；定义失谐因子σi=Qi(ω/ω0-ω0/ω)，用来衡量失谐程度。为了更好地反映三线圈系统线圈之间相互耦合的关系及有功功率的关系，可将中间变量定义为虚拟耦合因数ki(i=1，2，3)[15]：

(5)

式中：k1为发射线圈与中继线圈的虚拟耦合因数；k2为中继线圈与接收线圈的虚拟耦合因数；k3为发射线圈与接收线圈的虚拟耦合因数。

在一次侧为了实现逆变器软开关状态，往往需要采用失谐补偿参数使一次侧的电压相位略超前于电流，此时一次侧电压、电流存在一定程度的失谐角度，即σ1≠0;而其余2个谐振线圈采用谐振补偿(σ2=σ3=0)时，根据式(2)—式(5)得到输出功率P为

(6)

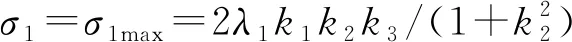
(7)

将式(6)、式(7)归一化得到输出功率增益:

(8)

式(8)中输出功率增益α可以表征输出功率的大小。根据式(8)可得到在不同虚拟耦合因数下输出功率增益与失谐因子的关系曲线。在λ1为0.42，1.25情况下不同虚拟耦合因数、失谐因子与输出功率增益的关系曲线如图3、图4所示。

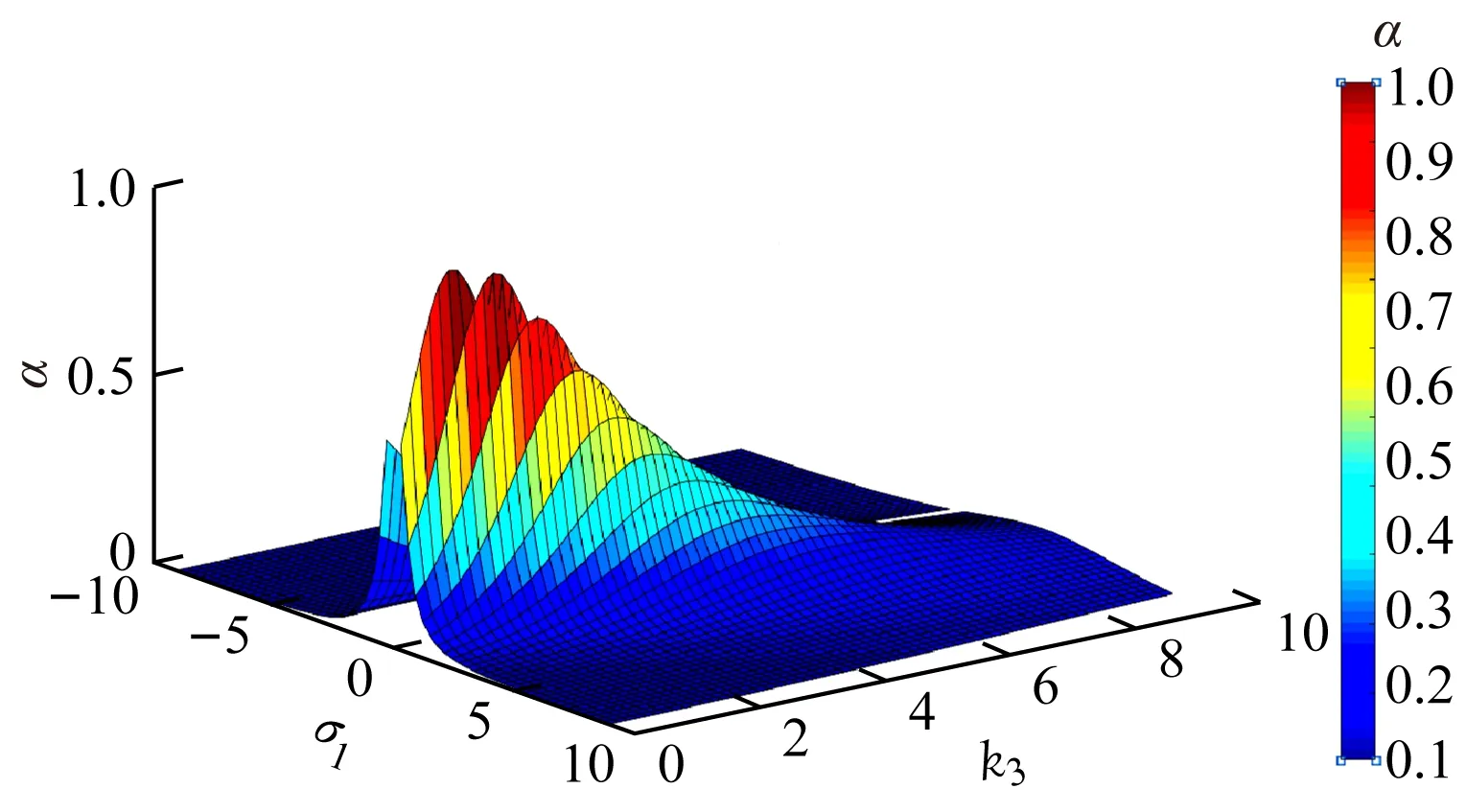
(a) k1=2，k2=2

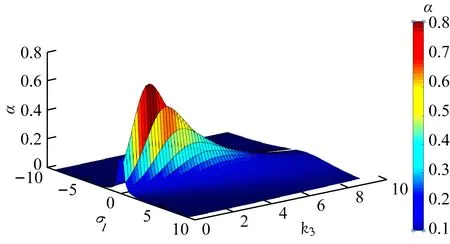
(b) k1=1，k2=2

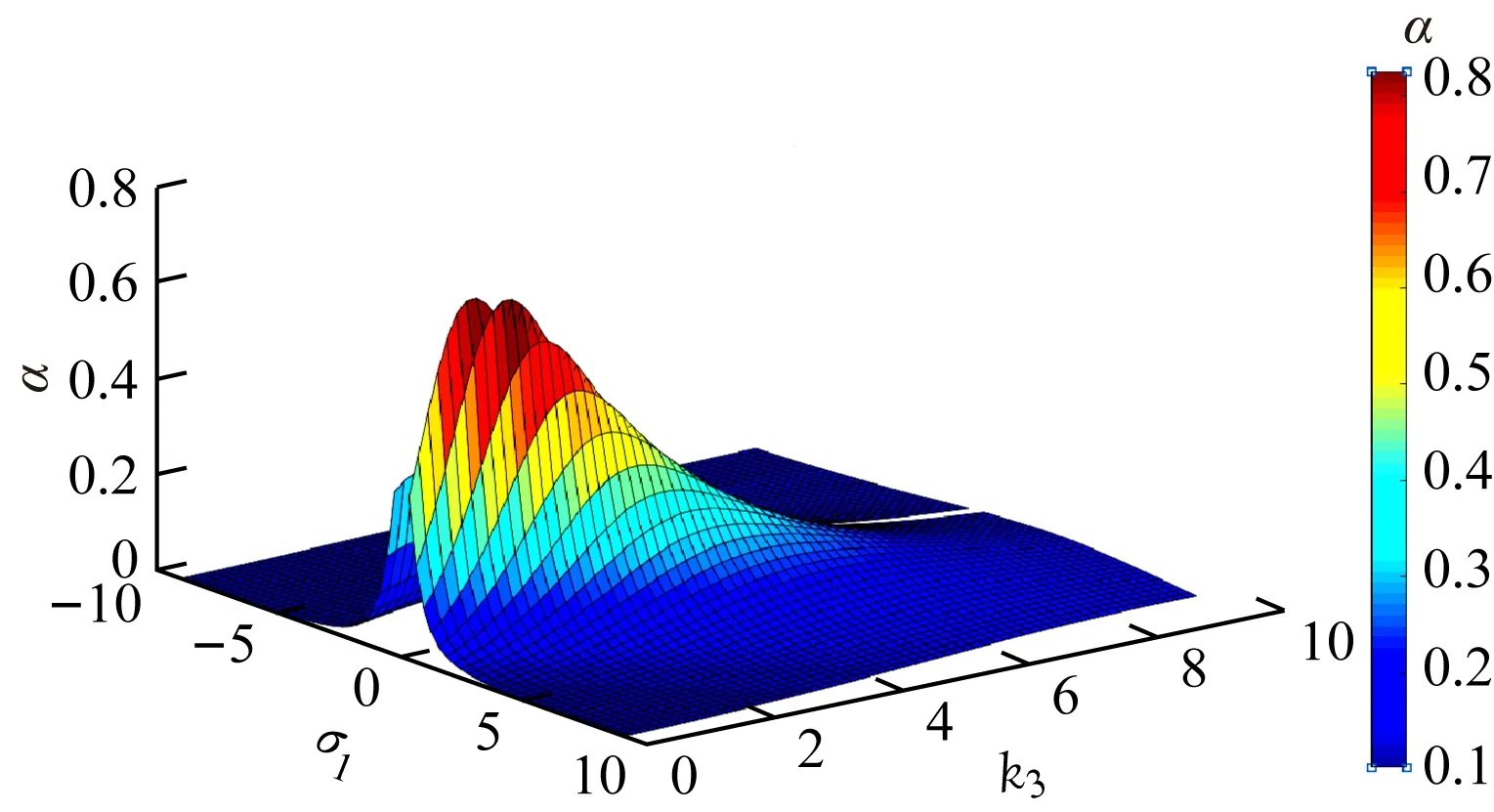
(c) k1=2，k2=1

从图3可看出：0<λ1<1时，随着失谐因子的

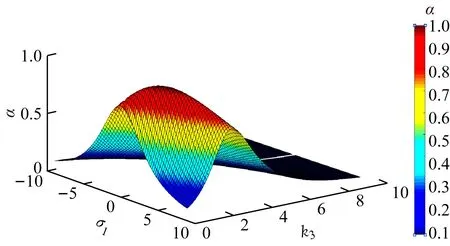
(a) k1=2，k2=2

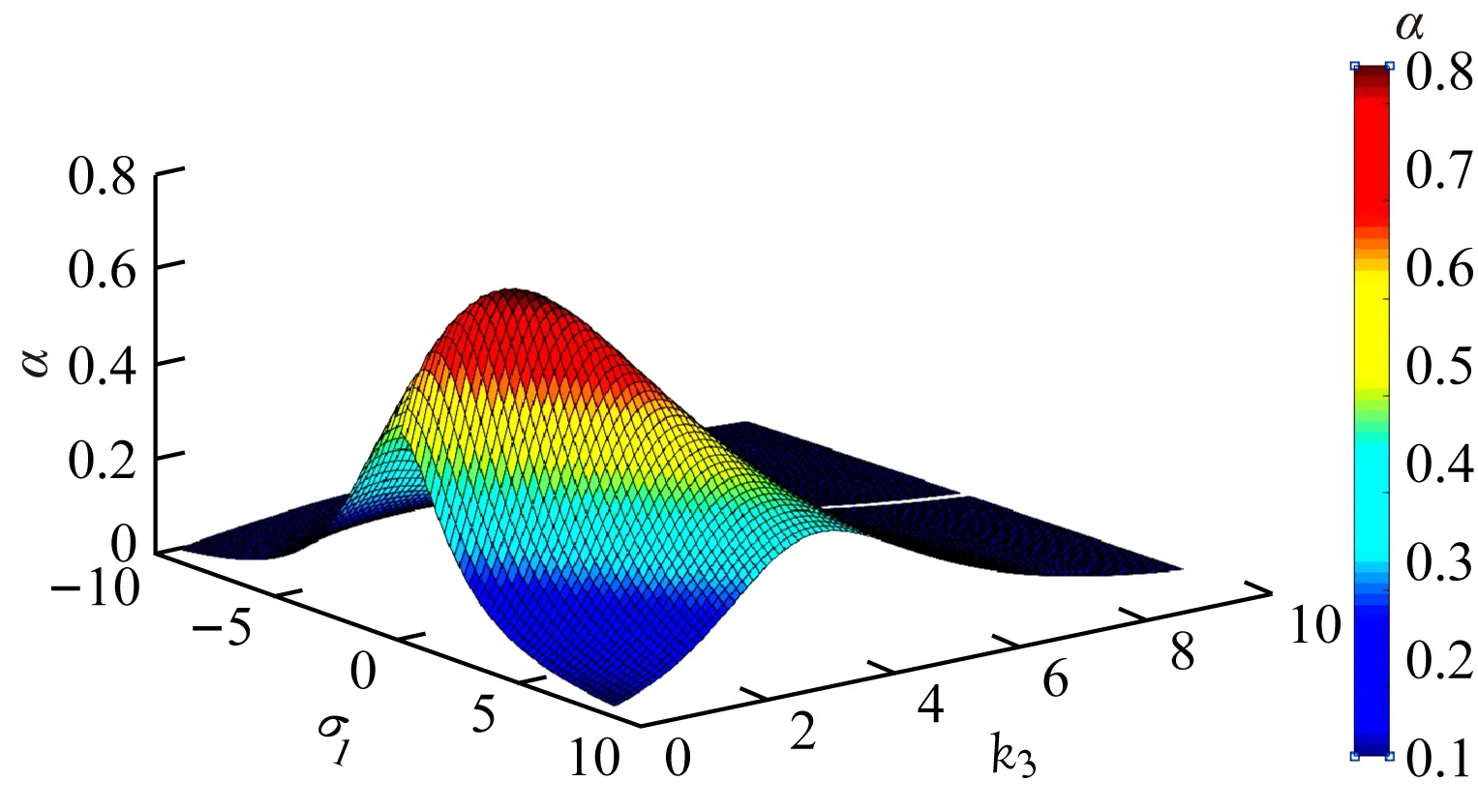
(b) k1=1，k2=2

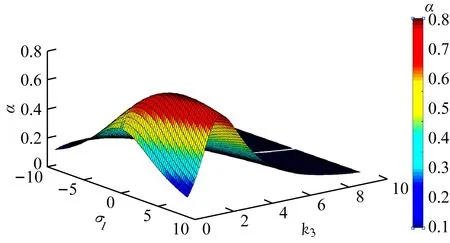
(c) k1=2，k2=1

变化出现了多个输出功率峰值，这表明系统的谐振频率出现了漂移，导致输出功率出现多个峰值，即此时存在频率分裂现象；k1=k2=2时，在k3=1，σ1=0.672处，α取得极值0.97；k1=2，k2=1时，在k3=1，σ1=0.84处，α取得极值0.74；k1=1，k2=2时，在k3=1，σ1=0.336处，α取得极值0.74。从图4可看出：λ1≥1时，只出现了单个输出功率峰值，即这时不存在频率分裂现象；k1=k2=2时，在k3=1，σ1=2时，α取得极值0.99；k1=2，k2=1时，在k3=1，σ1=2.5，α取得极值0.77；k1=1，k2=2时，在k3=1，σ1=1，α取得极值0.77。

综合图3、图4分析可得到如下结论：

(1)λ1的大小可表征系统是否存在频率分裂现象。当0<λ1<1时，系统的输出功率出现了多个峰值，即此时存在频率分裂现象；当λ1≥1时，系统只存在单个输出功率峰值，即这时不存在频率分裂现象。

(2) 当k1=k2时，系统的输出功率要大于k1≠k2时的输出功率，当k3=1时,系统的输出功率最大。

(3) 失谐因子σ1可衡量一次侧的失谐程度，σ1的取值越大，一次侧失谐程度越大；σ1的取值越小，一次侧失谐程度越小。

(4) 对于品质因数Q，当σ1为定值时，Q越大，工作频率ω与谐振频率ω0差值越小，此时失谐程度越小；当σ1为定值时，Q越小，工作频率ω与谐振频率ω0差值越大，此时失谐程度越大。为此，在考虑一次侧失谐参数设计时，宜适当选取较大的品质因数以降低失谐频率的波动。

当k1=k2，k3=1时，在σ1=σ1max处，输出功率增益α取得最大值，将k1=k2，k3=1代入式(5)，可得

(9)

式(9)可作为一次侧采用失谐补偿最优参数选择的依据。

3 实验结果与分析

为验证一次侧失谐补偿参数设计的合理性，搭建谐振频率f0为100 kHz的三线圈串联型MR-WPT系统实验平台，主要由直流电源、逆变器、DSP、谐振线圈、整流器和负载组成，如图5所示。表1给出了相应的电路设计参数。

图5 三线圈串联型MR-WPT系统实验平台Fig.5 Experimental platform of three-coil series MR-WPT system

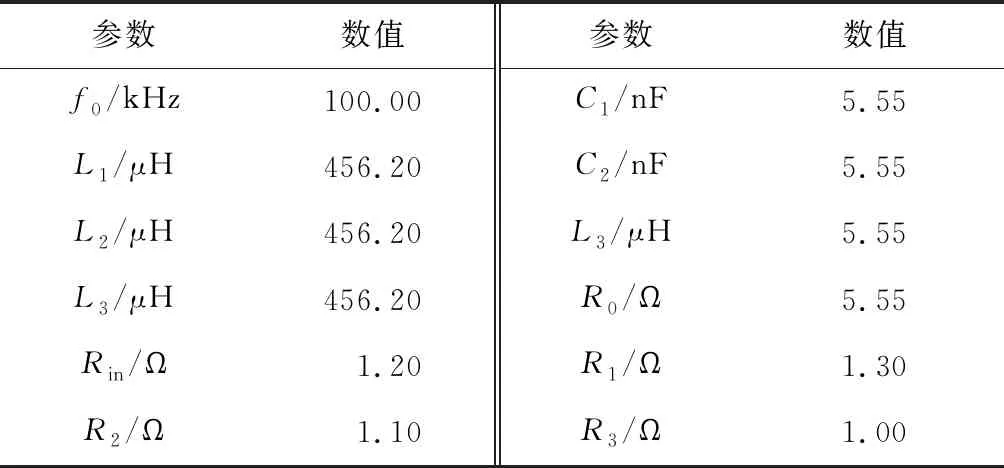
表1 三线圈串联型MR-WPT系统电路参数Table 1 Circuit parameters of three-coil series MR-WPT system

取σ1=2，λ1=0.42，1.25，在不同虚拟耦合因数下对系统输出功率进行对比实验。一次侧采用失谐补偿参数时的实验波形如图6所示，图6中,u1和i1分别为一次侧的交流电压与电流，U0、I0分别为负载直流电压与电流。表2给出了实验结果。从表2可看出：当λ1=0.42时，在k1=k2=2、k3=1处，P为18.8 W；在k1=k2=2,k3=0.1处，P为5.3 W；而在k1=1,k2=2,k3=0.1和k1=2，k2=2,k3=0.1处，P值相对较小。当λ1=1.25时,在k1=k2=2,k3=1处，P为26.7 W；在k1=k2=2,k3=0.1处，P为7.6 W；而在k1=1，k2=2,k3=0.1和k1=2，k2=2,k3=0.1处，P值相对较小。

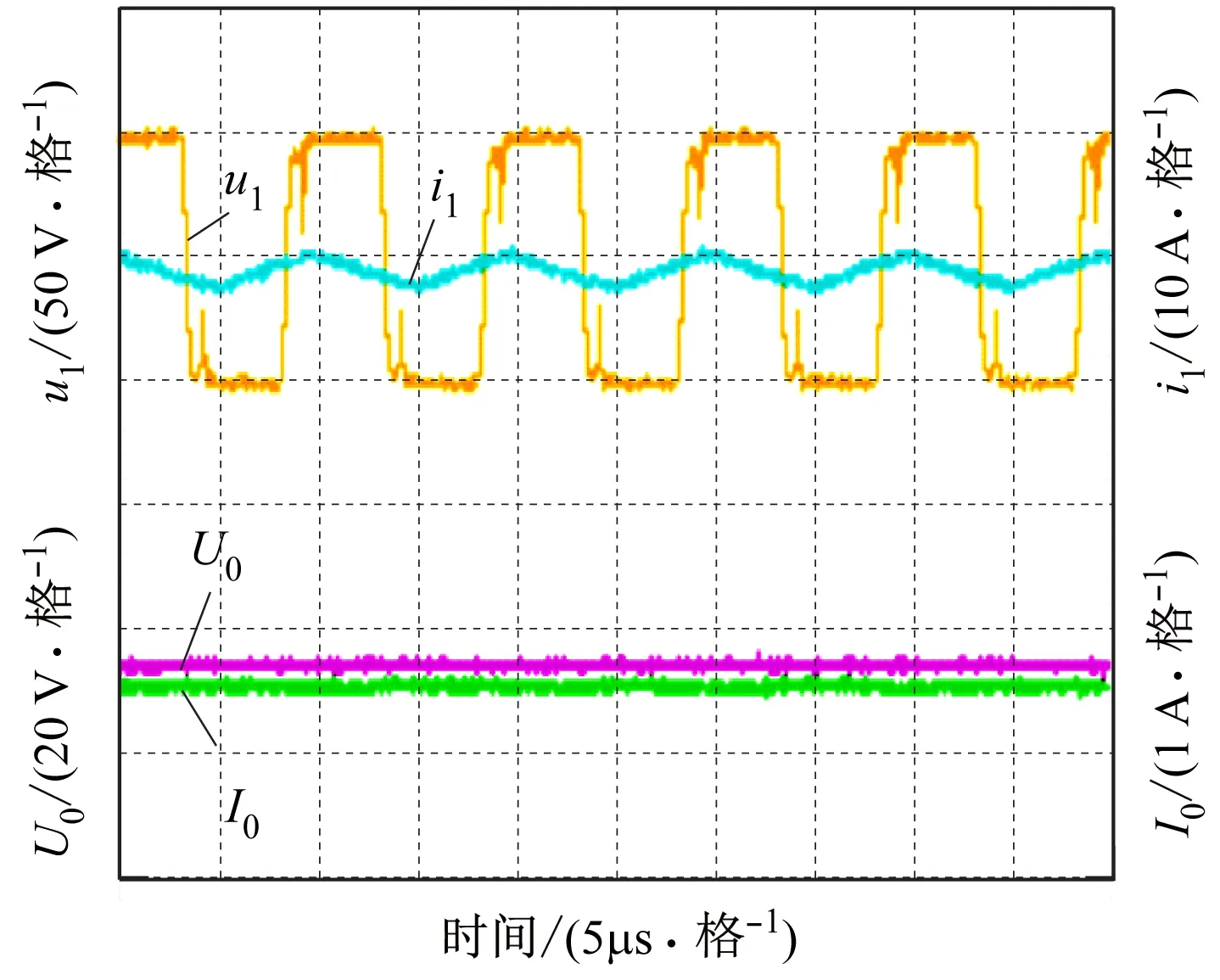
(a) λ1=0.42时的实验波形

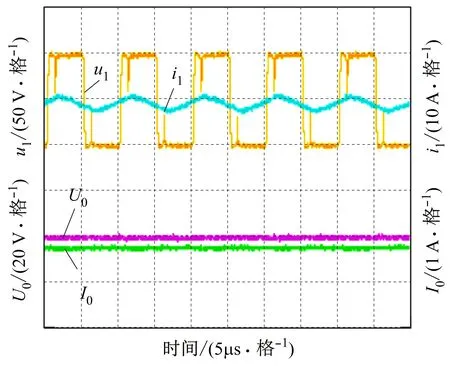
(b) λ1=1.25时的实验波形

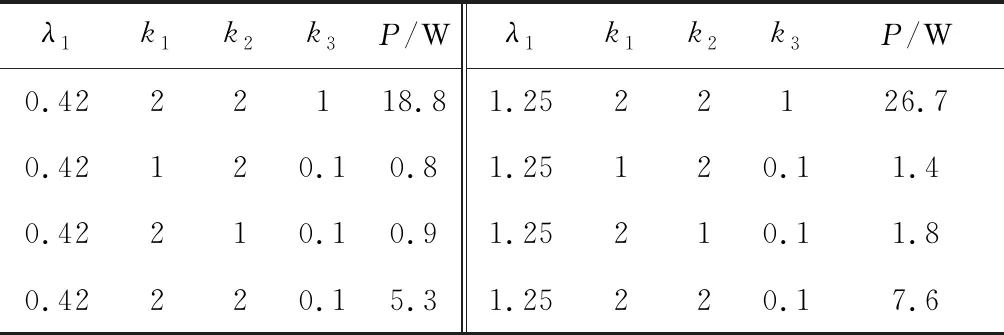
表2 不同虚拟耦合因数下系统的输出功率Table 2 Output power of the system under different virtual coupling factors

由表2可知，在其他参数均相同的情况下，k1=k2比k1≠k2时系统具有更大的输出功率；k1=k2且k3=1时系统可获得最大输出功率。表2的实验数据所呈现的规律基本和理论与仿真分析一致，验证了所设计的失谐参数的正确性。

4 结论

(1) 提出了一种MR-WPT系统一次侧失谐参数设计方法，通过引入虚拟耦合因数简化参数计算过程，无需复杂的算法与设计额外的硬件电路，具有一定的可行性。

(2) 研究了一次侧失谐参数对三线圈MR-WPT系统的影响，分析了MR-WPT系统3个线圈回路之间的不同虚拟耦合因数、失谐因子与系统传输功率的关系：发射线圈回路与中继线圈回路内阻比的大小可表征系统是否存在频率分裂现象；当失谐因子为定值时，发射线圈与中继线圈的虚拟耦合因数和中继线圈与接收线圈的虚拟耦合因数相等，且发射线圈与接收线圈的虚拟耦合因数相等时，系统输出功率最大。三线圈MR-WPT系统在一次侧采用失谐补偿参数时应遵循此规律来获取较大的输出功率。