基于pytorch的神经网络优化算法研究

姬壮伟

（长治学院计算机系，山西长治 046011）

深度学习是近年来发展十分迅速的研究领域，并且在人工智能的很多子领域都取得了巨大的成功，从移动端的人脸识别，到alphago机器人击败人类职业围棋选手，现代人的生活已经和人工智能密切相关。

人工神经网络是人工智能研究领域最热的深度学习模型，由早期的神经科学家受到人脑神经系统的启发构造而成，该网络是指由很多人工神经元构成的网络结构模型，这些人工神经元之间的连接强度便是可学习的参数。随着人工神经网络越来越复杂，数据越来越多，计算量急剧增加，我们需要在神经网络参数学习上花费的时间也就越来越多，可是现实中往往为了解决复杂的问题，复杂的网络结构和大数据又是不可避免的，神经网络的优化器便由此而生，通过优化算法加速神经网络的训练，加速参数的学习。

1 神经网络优化器发展

Gradient Descent，即梯度下降算法，由Cauchy,Augustin 于1847 年首次提出，依据数学理论解决了神经网络中参数学习的方向问题，基于此算法，往后的科研人员做出了许多优化。在1951 年，SGD 算法的早期形式被提出，随机梯度下降的参数学习方法被广泛应用，由于SGD 学习效率的局限，在1964 年，由Polyak 提出了Momentum 的优化算法，此算法利用给学习参数附加惯性值，大大提高了参数学习的效率。在神经网络兴起的这几年中，优化算法也从没停止发展，2011 年John Duchi 提出了通过优化学习率参数来提高学习效率的AdaGrad 优化算法，2015年Diederik P.Kingma 和Jimmy Lei Ba 提出的Adam 优化算法集合了Momentum 和AdaGrad 算法的优点，进一步提高了学习效率。在接下来的几年中，相继提出了AdaMax、Nadam、SGDW、Adabound、RAdam 等优化算法。

总体来说，目前的优化算法皆是从调整学习率和调整梯度方向两方面来优化训练速度，各优化算法汇总如表1所示。

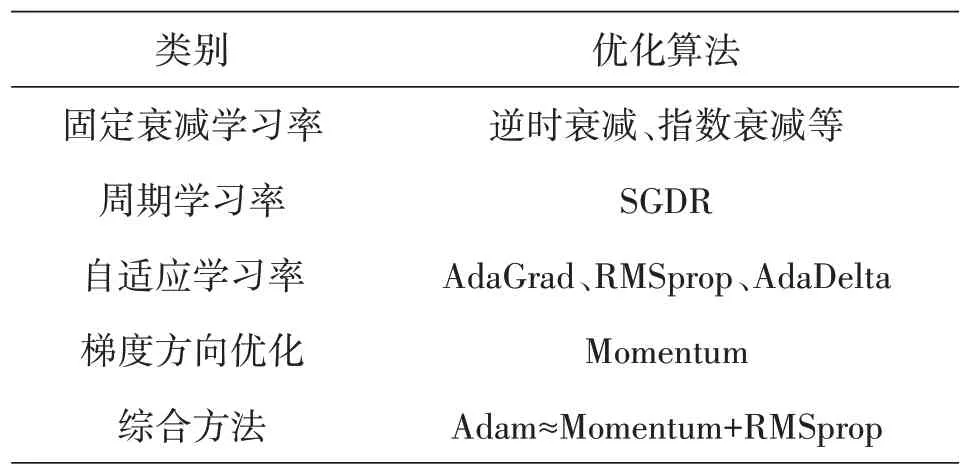
表1 神经网络常用优化算法汇总

2 神经网络优化算法

2.1 Stochastic Gradient Descent (SGD)

SGD[1-2]即随机梯度下降，是梯度下降算法的变种。批量梯度下降算法在梯度下降时，每次迭代都要计算整个训练数据上的梯度，当遇到大规模训练数据时，计算资源需求多，数据通常也会非常冗余。随机梯度下降算法则把数据拆成几个小批次样本，每次只随机选择一个样本来更新神经网络参数，如图1所示。

图1 SGD优化算法示意图

实验表明，每次使用小批量样本，虽然不足够反应整体数据的情况，但却很大程度上加速了神经网络的参数学习过程，并且还不会丢失太多准确率。

2.2 Momentum

动量是物理学中的概念，是指物体在它运动方向上保持运动的一种趋势，Momentum 方法[3-4]则将其运用到神经网络的优化中，用之前累计的动量来替代真正的梯度，计算负梯度的“加权移动平均”来作为参数的更新方向，其参数更新表达式为

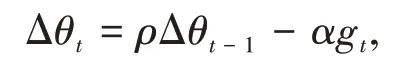
其中ρ为动量因子，通常设为0.9，α 为学习率。这样，每个参数的实际更新差值取决于最近一段时间内梯度的加权平均值，当某个参数在最近一段时间内的梯度方向不一致时，其真是的参数更新幅度变小；相反，当在最近一段时间内的梯度方向都一致时，其真实的参数更新幅度变大，起到加速作用，相比SGD，能更快的到达最优点。

2.3 AdaGrad

在标准的梯度下降算法中，每个参数在每次迭代时都使用相同的学习率，AdaGrad 算法[5]则改变这一传统思想，由于每个参数维度上收敛速度都不相同，因此根据不同参数的收敛情况分别设置学习率。

AdaGrad 算法借鉴正则化思想，每次迭代时自适应的调整每个参数的学习率，在进行第t次迭代时，先计算每个参数梯度平方的累计值，其表达式为

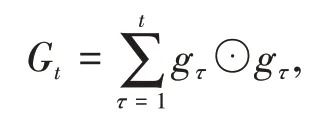
其中⊙为按元素乘积，gt是第t次迭代时的梯度。然后再计算参数的更新差值，表达式为

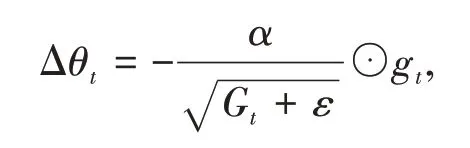
其中α 是初始的学习率，ε 是为了保持数值稳定性而设置的非常小的常数。

在Adagrad 算法中，如果某个参数的偏导数累积比较大，其学习率相对较小；相反，如果其偏导数累积较小，其学习率相对较大。但整体是随着迭代次数的增加，学习率逐渐缩小。

2.4 RMSProp

RMSprop 算法[6-7]对AdaGrad 算法进行改进，在AdaGrad 算法中由于学习率逐渐减小，在经过一定次数的迭代依然没有找到最优点时，便很难再继续找到最优点，RMSprop算法则可在有些情况下避免这种缺点。

RMSprop 算法首先计算每次迭代梯度gt平方的指数衰减移动平均，

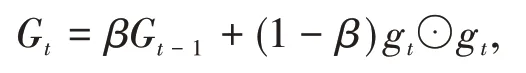
其中β为衰减率，然后用和AdaGrad 同样的方法计算参数更新差值，从表达式中可以看出，RMSprop算法的每个学习参数不是呈衰减趋势，既可以变小也可以变大。

2.5 Adam

Adam算法[8-9]即自适应动量估计算法，是Momentum 算法和RMSprop 算法的结合，不但使用动量作为参数更新方向，而且可以自适应调整学习率。

Adam 算法一方面计算梯度平方的指数加权平均（和RMSprop 类似），另一方面计算梯度的指数加权平均（和Momentum法类似），其表达式为

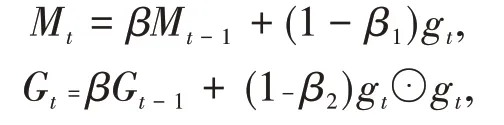
其中β1和β2分别为两个移动平均的衰减率，Adam算法的参数更新差值为

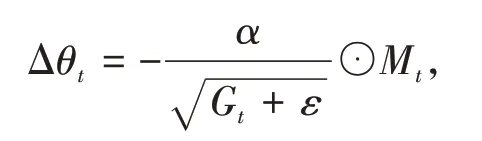
Adam 算法集合了Momentum 算法和RMSprop 算法的优点，因此相比之下，Adam 能更快更好的找到最优点，迅速收敛。

3 优化性能实验设计及结果分析

使用由Facebook 开源的Pytroch[10]神经网络框架，该框架是基于Python 的张量库，近几年和Tensorflow 成为该研究领域的主流框架，并且通过Python 的Matplotlib 可视化工具包将实验结果展示出来。用神经网络领域典型的回归问题来测试我们不同优化算法的参数学习效率和收敛速度。

3.1 生成训练数据

训练数据为5000 个伪数据点，由平方曲线的正太上下浮动生成，训练时的批量大小为64，学习率为0.01，如图2所示。

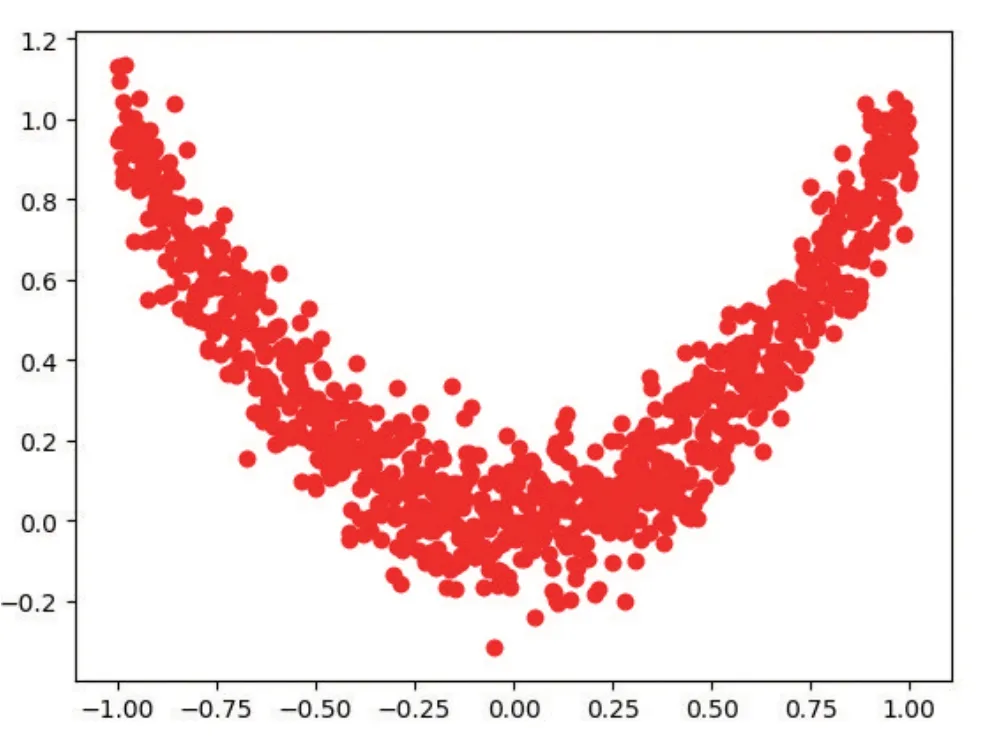
图2 实验数据展示图

3.2 创建与训练神经网络

每个优化算法使用的都是同一个神经网络，本实验中搭建的神经网络的输入层包含1 个输入神经元，共两层隐藏层，每层隐藏层包含20 个神经元，输出层包含1 个输出神经元，每层神经网络这件用RELU激活函数进行激活，神经网络搭建好后，用不同的神经网络优化算法对同一神经网络进行参数优化，对比不同优化算法的参数收敛速度，以及训练误差，并通过Matplotlib 可视化工具对结果进行可视化展示，如图3所示。

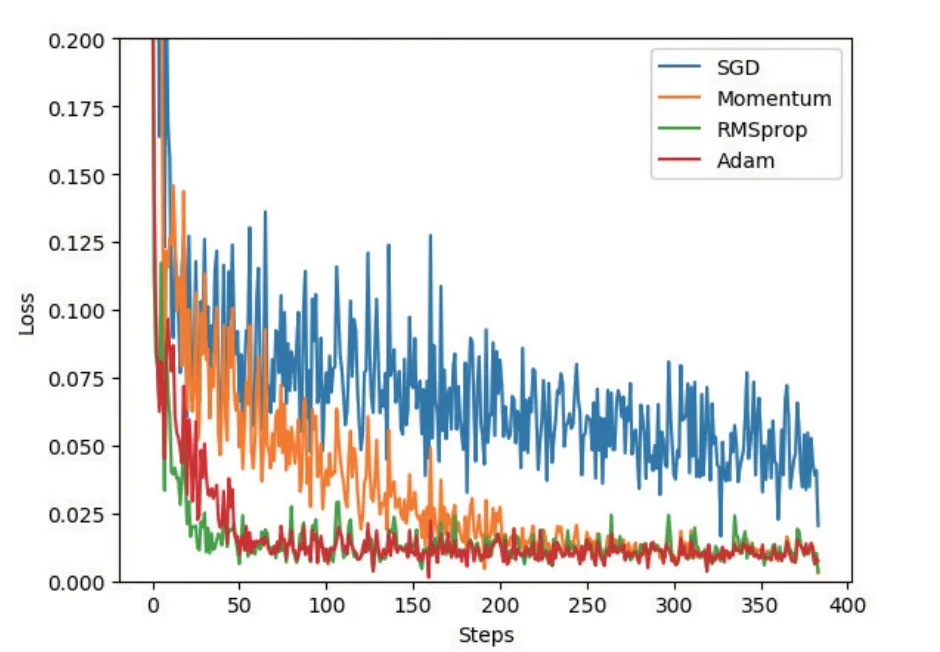
图3 不同优化算法收敛展示图

图3 中横轴为训练时间线，纵轴为误差率，在同一图中展示了不同的优化算法在同一神经网络的参数收敛速度，以及不同优化算法的误差率。

3.3 测试及结果分析

通过用不同优化算法对同一神经网络的多次训练，可以看出，几乎没有任何加速效果的SGD 优化算法参数收敛速度最慢，且误差率最高，而将SGD 改良后Momentum 则由于动量的存在，相比之下参数更快的收敛，误差达到一个稳定的低值，而RMSprop 和Adam 是进一步优化算法升级，明显收敛速度逐步增加，误差率更早达到稳定状态。

4 结论

优化算法对神经网络的学习效率影响很大，如今的优化算法从调整学习率和调整梯度两个方向，来优化训练速度，在神经网络处理的不同数据中，要多次尝试选择合适的优化器才能让神经网络的性能最大化。