纤维素中水分子扩散行为的分子模拟研究

解紫茹 刘刚 陈姗姗 赵红霞 李梦雪 甘长德

东华大学环境科学与工程学院

0 引言

纤维素是天然纤维重要的组成部分，是最丰富、储量最大的可再生资源。同时，由于天然纤维素含有许多亲水的羟基基团，具有显著的吸放湿性能优势，在常温常压下就具有较高的吸放湿速度和较大的蓄湿容量。这种吸附性可开发出对环境湿度具有调节能力的调湿材料，无需浪费能源即可改善环境舒适度。因此，了解纤维素材料的吸附能力与吸湿特性对纤维素材料在暖通领域的开发与应用具有重大积极意义。当前，随着人们环保意识增强，以及对纤维素良好的水蒸气吸附能力的认识，研究人员已经加大了对纤维素材料的研究与开发[1]。

目前纤维的吸湿性研究主要是通过实验手段获取纤维材料的吸湿等温线，以此来描述纤维吸湿和去湿的过程，探讨相关参数改变对材料性能的影响，但缺乏对微观作用机理的分析，难以解释微观作用的机理。分子模拟技术作为理论和实验之外的第三种研究手段，可从分子层面研究实验不能测得的现象及微观物理过程[2]，通过模拟提取出能反映物质变化规律的信息，进而揭示材料的微观结构与其宏观性能之间的关系，帮助研究者更为微观的研究吸附现象和机理，加深对材料的认识[3]。

本文建立无定形纤维素的模型，采用分子动力学手段研究水分子在无定形纤维素内的扩散和吸附行为，研究不同的水分含量对水分子在纤维素内的扩散性质所产生的影响，运用吸湿理论、扩散理论等剖析水在纤维素中的传输机理，为选择和开发性能优良的吸附材料提供思路和指导。

1 模拟方法和模型

1.1 模拟方法

本文使用Materials Studio 软件的Amorphous Cell和Forcite 模块完成。东华大学黄双[4]利用MS 软件构建纤维素Iβ 晶胞模型，软件计算了晶体的热膨胀系数与实验比对，验证了PCFF 力场、1fs 的步长的合理性，因此本文采用PCFF 力场、1fs 时间步长。为使计算中系统的密度维持恒定，采用周期性边界条件。温度控制采用Andersen thermometer[5]，压力控制采用Berendsen barostat[6]，范德华相互作用采用Atom Based加和，静电相互作用采用Ewald 加和。本文主要使用NVT 和NPT 系综。

1.2 模型构建

1.2.1纤维素纤维结构

纤维素是由β-D-吡喃葡萄糖基以1-4-β-苷键连接而成的线性高分子，分子链内的排列情况有结晶区和无定形区（又称非结晶区）。结晶区内纤维素链段沿纤维轴向几乎平行排列，无定形区内纤维素链段处于无序状态，存在较大的缝隙和孔洞，如图1 所示。结晶区排列整齐，性质稳定，水分子作用仅限于表面，难以进入结晶区，而无定形区结构松弛，分布不规律，内部存在较多的空穴，水分可以自由穿透无定形区。水和纤维素之间的相互作用基本上都集中在纤维素无定形区中[7]，因此本文将纤维素的无定形区作为研究的对象。

图1 纤维素链有序区域和无定形区域

Mazeau 等[8]模拟试验了3 种链长的纤维素无定形模型，发现不同的分子构型在物理化学性上的差异并不明显，得出计算结果和初始链长无关的结论。综合考虑计算时间及与自然纤维素接近程度，本文选择DP40（80 个葡萄糖单元）来构建纤维素链段。

1.2.2不同含水量纤维素模型

纤维吸湿后可用回潮率来表示含水量的多少，回潮率是用纤维材料中所含水分的质量占其干燥质量的百分比来定义，纤维在标准大气条件下的回潮率基本在14%以下[9]，于是本文首先建立了8 个模型，水分的质量分数分别是0、2%、4%、6%、8%、10%、12%、14%，用以研究水分和纤维素之间的相互作用。每个模型有2 条纤维素链。本文定义水分质量分数的计算同回潮率一致，均为水分的质量与纯纤维素的质量比值。Mazea[8]定义1 个水分子比上1 个葡萄糖单元质量分数为12%，所以不同构型水分子数目分别是0、15、30、43、58、72、87、101 个。其中初始密度设为1.5 g/cm3[10]，模型均根据Theodorou-Suter[11]提出构建周期性边界条件的立方单元来构建模型。以纯纤维素模型和水分质量分数为12%的构型为例，构建的无定形纤维模型如图2 所示。

图2 无水和含水量12%纤维素模型

1.3 模型验证

分子模拟的模型验证主要依靠密度来确定，密度是评估微观结构模型真实性的相关参数[12]。部分学者指出晶相的密度可由模拟的晶胞尺寸来估算[13]，实验测得的Iα 和Iβ 晶相的密度在1.582 到1.599 g/cm3之间，一般非晶相的密度比晶相的低10%～20%，最终得出无定形结构的密度应该在1.28～1.44 g/cm3范围内，聚合物手册[10]给出的纤维素无定形部分的密度在1.482～1.489 g/cm3。由此可见，无定形区纤维素由于结构复杂性，密度取值在一定区间内。表1 给出了温度为303 K 时，水分质量分数在0～14%的系统动力学模拟平衡后的平均密度，不含水分子的无定形结构的密度为1.436 g/cm3，是一个合理的数值，验证所建模型是正确的。在搭建模型的过程中，由于模块生成无定形结构的多样性，密度会随着模型搭建的参数的不同而在一定范围内变化。

表1 303 K 下不同含水量系统的平均密度

1.4 计算过程

模型搭建后的第一步需要对模型进行结构优化。包括能量最小化与退火（Anneal）过程，最终模型能量趋于稳定，获得能量最低的稳定吸附构型且表现得性质更接近真实材料。最后进行分子动力学模拟，对模型进行100 ps 的NPT 和1500 ps 的NVT 系综的动力学模拟。

生态环境保护面临一定困难和挑战，存在许多不足。一些地方和部门对生态环境保护认识不到位，责任落实不到位；经济社会发展同生态环境保护的矛盾仍然突出，资源环境承载能力已经达到或接近上限；城乡区域统筹不够，新老环境问题交织，区域性、布局性、结构性环境风险凸显。当前，生态文明建设正处于压力叠加、负重前行的关键期，已进入提供更多优质生态产品以满足人民日益增长的优美生态环境需要的攻坚期，也到了有条件有能力解决突出生态环境问题的窗口期。

2 结果与讨论

2.1 水分子扩散系数

高分子材料吸湿的动力主要来源于水分的扩散。在材料吸附水分子过程中，就是水分子通过扩散运动迁入材料体内，这一过程可采用Fick 定律描述[14]。扩散系数是作为评价扩散能力的一个重要的物理性质之一。一般来说，扩散系数的大小受扩散物质和扩散介质种类以及所处温度压力环境影响。根据爱因斯坦扩散定律，扩散系数可由水分子的均方位移确定，即：

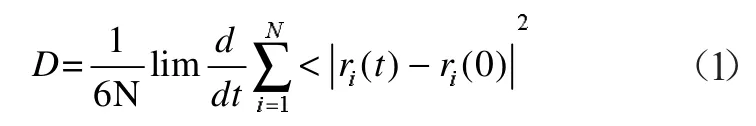
式中：N 表示系统粒子个数；ri(0)和ri(t)分别表示第i 个粒子的质心在时间步长下的起始位置和最终位置；尖括弧<>代表均方位移的系统平均。MS 的均方位移（Mean Square Displacement，MSD）对时间微分的比值可以近似替代式（1）的微分部分，由于MSD 已经对扩散原子数做了平均，所以式（1）也可以简化为：

式中：k 为MD 模拟得到的MSD 对时间t 所作曲线经过最小二乘法拟合得到的直线的斜率。Einstein 方程假设扩散粒子做跳跃式的跃迁运动，这种扩散过程称为正常扩散，根据MSD 的对数（log MSD）与时间对数（log t）关系曲线的斜率（n）可以判断粒子是否为正常扩散。如果n<1，则扩散粒子属于非正常扩散，也即是粒子局限在某一个空穴内运动。如果n 近似等于1，说明粒子的扩散运动属于正常扩散，即粒子在空穴之间跳跃式的运动[15-16]。

图3 给出了MD 模拟得到的不同水含量混合体系中的log MSD 与log t 关系曲线。由图3 可以看到，在整个模拟时间中，log MSD 与log t 关系曲线的斜率在不断改变，经过数据处理只有其中一段的斜率接近于1，说明随着时间的推延，水分子在纤维素中的扩散行为均由非正常扩散转变为正常扩散再转变为非正常扩散。因此，选取图3 中斜率接近于1 的模拟时间段，对MSD 图拟合直线，从而得出水分子在纤维素内的扩散系数，得到的扩散系数如表2 所示，其中R2代表拟合优度。

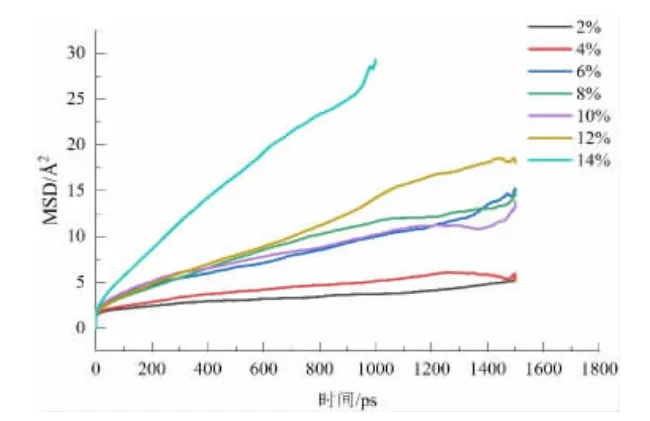
图3 不同水含量混合体系中的log MSD 与log t 曲线

表2 303 K 下不同含量水分子的扩散系数

由表2 数据可知，在303 K 水分质量分数为4%的情况下，水分子在纤维素内的扩散系数数量级在0.8167×10-11m2/s，Mazeau[17]建立的水分质量4.6%的模型的扩散系数为0.6×10-11m2/s，实验拟合求得的300 K下水分在纤维素中的扩散系数为3.16×10-11m2/s，310K的扩散系数为7.58×10-11m2/s[18]，模拟的结果有参考的意义。

2.2 相互作用能与自由体积对扩散作用的影响

水分子在纤维素中的扩散受各种因素的影响，其中，最重要的因素是水分与纤维素的相互作用和纤维素—水系统中自由体积的大小。

根据PCFF 力场，系统的总势能可以分解为键能（包括键、键角等），非键能（包括范德华作用和静电作用），整个系统的势能可以简单表达为下式：

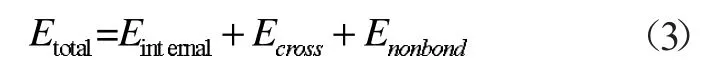
相互作用主要是指范德华作用力和静电作用力这些非键作用力，在表征物质之间相互作用时，它们统称为相互作用能。PCFF 力场在计算氢键键能时，没有将氢键作用作为单独项考虑，将其包含于范德华作用和静电作用之中，因此，水分子和纤维素之间的相互作用能不能由软件数据直接得到，需要运行计算相互作用能的Perl 脚本程序获取。

两种物质之间的相互作用能与总势能之间有如下关系：

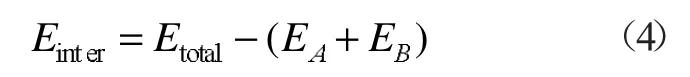
式中：Einter代表相互作用能；Etotal代表总势能；EA+EB代表物质A 和物质B 的势能之和。

计算值为正值代表排斥作用，负值代表结合作用，且绝对值越大，强度越强。图4 是水分含量2%的纤维素体系通过Perl 程序提取的相互作用能变化曲线，分别表示纤维素和水体系，纯纤维素体系，纯水体系和两种物质之间的相互作用能。在水分质量2%的体系中，纤维素和单个水之间的平均能量为310.53 kJ/mol，纤维素模型的平均能量为381.93 kJ/mol，水分子的平均能量为2.73 kJ/mol，所以经计算后的相互作用能为-74.13 kJ/mol，体现两种物质之间的相互吸引的作用。

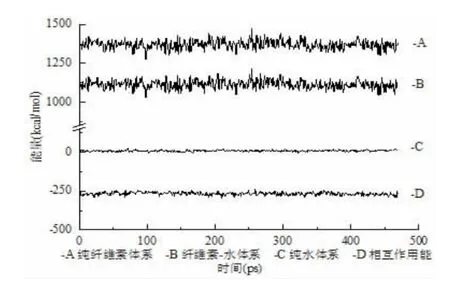
图4 含水量2%纤维素模型相互作用能曲线

将不同含水量的纤维素-水的体系相互作用能的各个成分进行了统计平均，经过编写的脚本计算后，相互作用仅包含静电作用和范德华作用，如图5 所示。从图中可以看出各体系中的相互作用均为负值，说明体系中纤维素介质与水分子之间存在不同程度的结合作用。而在相互作用中静电作用所占比例较大，范德华力所占比例小，体现了相互作用带有极性效应。随着纤维素模型中水分含量的增多，总相互作用能和其组成静电作用、范德华作用能都在逐渐减小，均呈现线性变化。从变化幅度来看，静电作用的变化幅度与相互作用能较为一致，而范德华作用虽然也是随着水分的增加作用减弱，但是变化的幅度不如静电作用，表明水分的加入，对静电作用项影响较大，极性对这种极性介质的相互作用起到一个主要作用。范德华作用力为距离的函数，范德华作用力随着体系内水分子的增多而减小，说明在远程上水分子与纤维素介质之间的平均距离在拉大。在水分含量2%的时候，水分和纤维素之间的结合能为74.13 kJ/mol，在水分含量14%的时候，结合能为55.71 kJ/mol，无定形纤维素对水分子扩散的束缚作用较大，这导致扩散系数的量级在10-11级别。

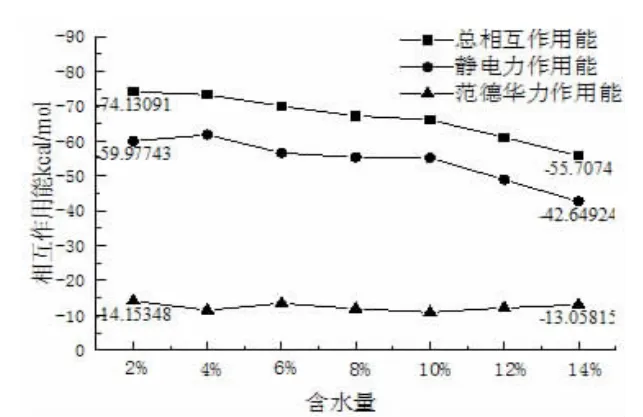
图5 不同含水量体系的平均相互作用能

在无定形纤维素和水分子组成的系统中存在着两种相态：聚合物分子链的固体相和自由体积的空间相。自由体积理论指出，自由体积是纤维素链和小分子发生扩散运动的空间场所。聚合物占据的体积称为占有体积（Occupied Volume，VO），以空穴形式存在的称为自由体积（Free Volume，VF），总体积为两者之和，自由体积分数（Fraction Of Free Volume，FFV）为自由体积与总体积的比值。

本文采用硬球探针方法计算自由体积。将水分子作为探测分子，其范德华半径为利用MS 软件的Atom Volume&Surface 测得了不同水含量下纤维素模型的自由体积特性如表3 所示，图6 显示了各项体积变化的曲线图以及FFV 随着水分子含量的增加的曲线图。不含水分子的纤维素占有体积为3，自由体积为，FFV 为0.0327。随着水分子数目的增多，纤维素的总体积和占有体积均呈现线性增长的线性，自由体积随之减少，FFV 下降减少。水分子数目增多，使得纤维素模型体积增大，水分子占领了纤维素内的空穴，导致系统的FFV 降低。

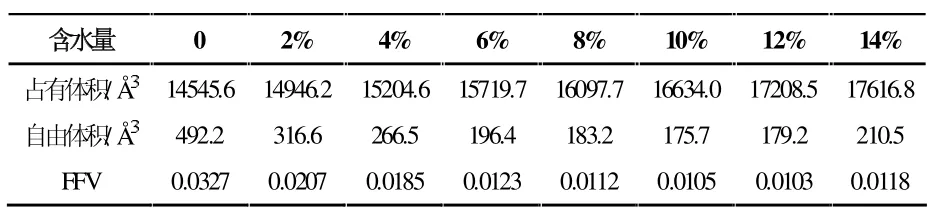
表3 不同含水量纤维素模型的自由体积

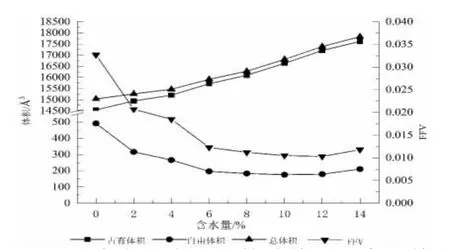
图6 不同含水量水分子的总体积和自由体积

水分子在纤维素中可能的运动形式有两类：一是在小范围内发生自身运动，二是在不同空穴中移动。水分子在大部分时间会停留在纤维素的孔洞中，形成扩散运动是通过由一个孔洞跳跃到另一个孔洞完成。如果在某个时刻，聚合物链由于热力性移动，恰好形成了能够到达附近孔洞的通道，水分子就脱离现有的位置跳跃进入新的孔洞。所以水分子在纤维素的扩散过程就是由水分子在孔洞中的随机振动，然后偶然跳入附近的孔洞这些连续过程构成。

根据自由理论，自由体积的减小，可能导致小分子的扩散系数变小，但结合本文的计算结果，在0～14%纤维素—水体系反应出的规律是随着水分子加入数目越多，扩散系数越大，这说明在综合考虑影响扩散系数大小的原因时还需要综合考虑其他因素。本文发现FFV 在0～14%体现的主体规律是越来越小，但14%体系反而变大，这也是水分子含量14%体系扩散系数有巨幅增长的原因之一。

2.3 吸附形态分析

观察表2 中的数据，发现水分子扩散系数随含水量变化产生了不同程度的增长，在含水量2%～6%、12%～14%两个阶段增长迅速，自由体积的变化可以解释第二阶段增长迅速的原因。为了研究第一阶段扩散系数增长速度发生变化的原因，本文建立水分含量3%与5%的模型，按照前文模拟方法进行模拟运算，将计算结果汇总整理为图7，并计算每个阶段扩散系数变化率整理与表4。可以看到，扩散系数在5%～6%、12%～14%两个阶段的变化程度明显高出其他阶段，水分子扩散系数产生了巨大增长。

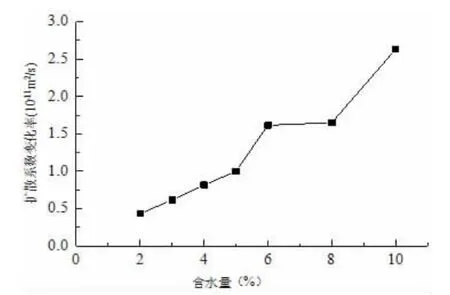
图7 303 K 下不同含水量的扩散系数曲线

表4 303 K 下不同含量水分子扩散系数变化率

径向分布函数（Radial Distribution Function，RDF）用以描述模型中原子的分布情况，图中纵坐标g(r)表明一个分子周围距离为r 的位置上出现另一个分子的概率比值，是一个量纲为1 的函数。若径向分布为1 则代表粒子随机分布，不存在有序性。根据文献指出，当两个水分子之间的距离大于则两个分子相互独立的，由于分子在纤维素模型中是不断运动扩散的，若在扩散时间内的80%时间水分子和其他水分子相互远离，则说明其是孤立的。而若扩散时间内的80%时间水分子和其他水分子相互聚集，则说明水分子之间是聚集的。用RDF 图来说明水分子和水分子之间的距离，借此描述水分子在纤维素内的吸附形态，图8 给出了水分子中氧原子之间的径向分布函数图。

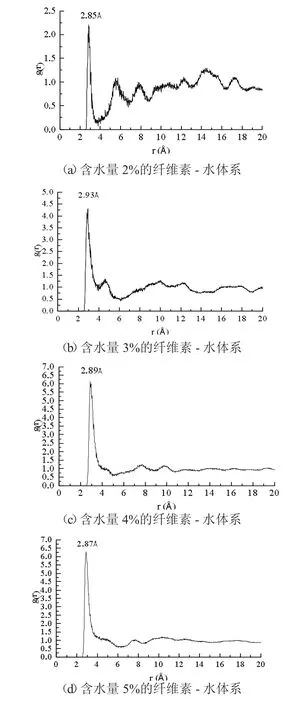
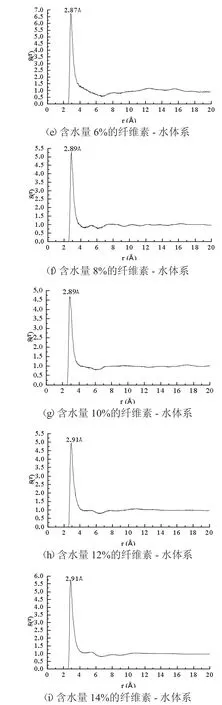
图8 不同体系水分子的RDF 图

水分在纤维素内部的聚集状态可以是单分子独立的，也可以是形成团簇聚集的。从图8 中可以看出，不同含水量体系，在r 小于左右时，径向分布函数g(r)均为0，水分子间互相排斥；不同水分含量的系统都在附近出现峰值；在水分含量2%、3%体系内g(r)呈现剧烈变化，在水分含量4%、5%的体系中，g(r)存在2～3 个峰值，由径向分布函数g(r)可以判断，在2%～5%四个体系中，大部分水分子以聚集形态存在，为多层吸附，同时还存很少部分的水分子是以个体单分子在纤维素内，形成单层吸附。从水分子含量6%开始的模拟体系中都存在r 为2.87～2.91的峰值，而在r 大于左右时，径向分布函数g(r)都趋于1，水分子的分布在纤维素内部是无序的。从径向分布函数的可以判断，体系中的水分含量在5%～6%之间的某个状态下，水分子数量增多，水分子发生凝聚，以聚集态形式结合吸附，水分子的吸附形态发生了改变，由单层吸附与多层吸附共存发展成为只有多层吸附，吸附形态的变化可以解释水分子扩散系数在5%～6%体系明显增大的原因。

3 结论

本文采用分子模拟对水分子和纤维素的相互作用进行了研究，利用分子动力学手段探究了水分子在纤维素中的扩散和吸附行为，并对扩散和吸附机理做了解释。

1）利用分子动力学对纤维素中水分的扩散及影响因素做了研究，得到纤维素中水分子的扩散系数的量级在10-11m2/s 左右。此数值与实验下的扩散系数进行比较，数量级一致，证明该模型以及模拟方法可以用来求解小分子在纤维素中的扩散系数。

2）在纤维素体系中随着水分子的加入，扩散系数逐渐增大，含水量在5～6%、12～14%内扩散系数增幅较大，在6%～8%增长不明显。探究各相互作用能与自由体积对水分子扩散系数的影响，可以得到水分和纤维素的相互作用中静电力作用起到主要束缚作用。而含水量14%状态下FFV 变大可以解释含水量12%～14%扩散系数增长迅速。

3）分析了水分子中氧原子之间的径向分布函数可以得到，从无水状态到水含量逐渐增加的变化过程中，水分子开始时以单层吸附和多层吸附存在纤维素内，而随着水分子数目的增多，在5%～6%之间的某个状态下，水分子的吸附形式变为团簇的多层吸附，吸附形态的改变是导致含水量5%～6%扩散系数增长迅速原因。

本文使用的计算模型和计算方法可为研究纤维素吸附其他气体小分子以及水分子在改性纤维素吸附的理论研究提供思路，推动纤维素材料在调湿领域与暖通设备领域中的应用。