基于CSM模型的TBM滚刀受力预测公式

（中铁隧道局集团有限公司，广东 广州 511400）

1 前言

全断面岩石隧道掘进机（Tunnel Boring Machine，TBM）是一种专门用于开挖隧道的大型工程装备。在隧道施工时，TBM 可以不受天气变化的影响，具有掘进速度快、机械自动化程度高、对外界环境扰动小等特点。在TBM 掘进时，滚刀破岩的受力对于隧道掘进速度和掘进成本有着密切的联系。因此对盘形滚刀受力的深入研究是十分必要的。

2 滚刀受力分析

2.1 刀盘工况描述

TBM 滚刀在切削岩石时主要受到3 个方向的作用力：垂直于掌子面的法向推力FV（由刀盘整体推力所提供）、平行于掘进面的切向力Fr（由刀盘的扭矩所提供）、刀圈在贯入到岩石中受到侧向压力FN（这两个力近似乎平行）。其受力如图1所示。

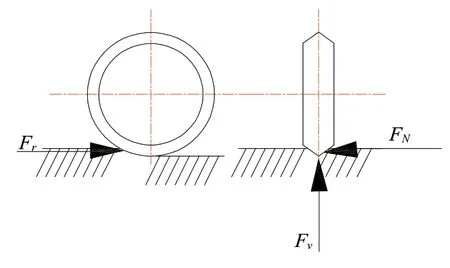
图1 滚刀破岩受力示意图

2.2 基于CSM模型刀具受力的分析

CSM 模型如下

式中Ft——推进过程中所受的合力；

R——滚刀的半径；

θ——刀刃角；

T——滚刀刀尖宽度；

ψ——刀尖压力分布系数；

φ——滚刀与岩石的接触角；

p——破碎区的任意一点压力；

p0——岩石破碎区的基本压力，p0=f（σc，σt，S，T，R，p）。

式中C——无量纲系数，与刀刃角的形状有关，C≈2.12；

σc——岩石单轴抗压强度，MPa；

σt——岩石单轴抗拉强度，MPa。

2.3 改进CSM模型

2.3.1 刀具切割时受力分析

CSM 模型是通过线性切割的实验得到的，并且可以通过CSM 模型公式看出此模型只考虑了滚刀正下方的破碎区的压力p，并通过积分计算出合力Ft，并通过刀刃角θ分解Ft，从而得到法向力Fv及切向力Fr。但是在实际情况下，会发现滚刀两侧会发生磨损，滚刀在破岩的过程中，不仅仅推力提供的法向力Fv及切向力Fr，还会受到岩石两侧对滚刀接触面产生的挤压力FN1与FN2。这一对力远远小于Fv与Fr，但是这是刀圈外侧磨损的主要原因之一。S1与S2分别是FN1与FN2对应的接触面积，如图2 所示。

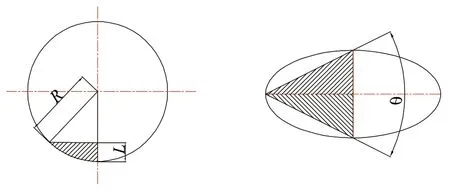
图2 刀圈侧面接触面积

结合CSM 模型及已知滚刀几何参数可以得出式（7）和式（8）。

因为岩石在破坏的临界点看作是弹性体，由于岩石破碎区域刀圈的受力十分复杂，为了研究和计算的方便，在这里将岩石两侧的不平衡压力FN1与FN2假设大小相同且方向相反，且在破碎区刀圈侧面压力也为p0。

假设在某一时刻，选取处于正上方且距离刀盘回转中心最远的正滚刀进行受力分析。此时的刀具正垂直于掌子面进入到岩石当中，并假设此时线速度方向水平向左。此时受力如图3 所示。

刀圈两侧所受的侧向压力FN1与FN2将产生摩擦力f1与f2以阻碍其运动，故其方向在此刻是水平向右，与切向力Fr相同。简化受力如图4 示。

图3 刀圈三维受力图

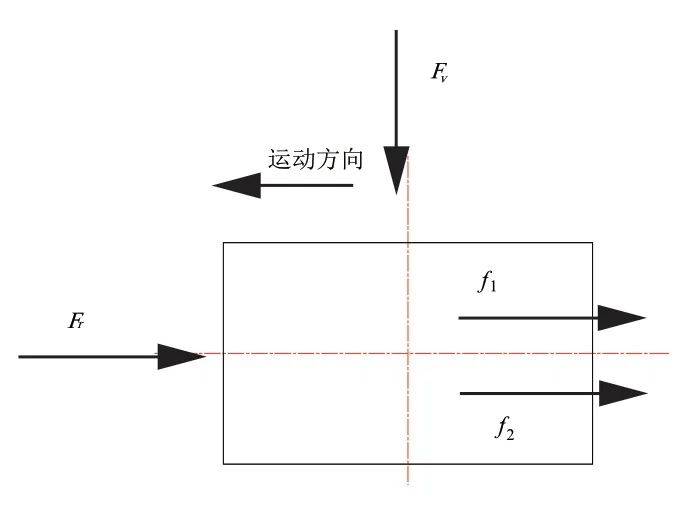
图4 简化刀圈二维平面受力图

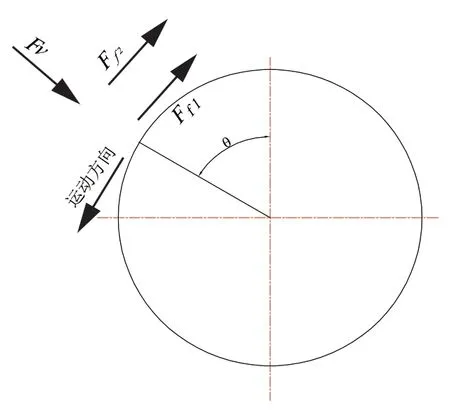
图5 任意时刻刀圈受力示意图

现在对处于任意一角度进行分析，如图5 所示，刀圈正处于距离回转中心θ角度，此时，其线速度方向是垂直于滚刀中心位置与刀盘回转中心的连线；由于所有滚刀是垂直于掌子面安装的，所以法向力Fv始终垂直于刀圈，且并不产生摩擦力。由于刀圈扭矩所产生的切向力是与线速度方向相反，因此刀圈两侧的侧向力所产生的摩擦力方向是阻碍其运动方向，所以也与线速度方向相反，即Fr1和Fr2与Fr方向相同。

2.3.2 对CSM模型的修正

改进后的CSM 模型

式中μ——刀圈与岩石之间的摩擦因数。

3 改进后的CSM模型验证

3.1 实际案例

以新加坡C885 项目的中铁658 号盾构为例进行分析。截至2020 年5 月，已累计掘进472 环，期间共经历3 次换刀：在103 环，更换了部分保径刀及中心滚刀；在272 环，更换了部分保径刀；在353 环，对11 把保径刀及30 把滚刀进行了全部更换。因为刀具的几何尺寸对CSM 模型的计算产生了重要的影响，且掘进过程中地层的不确定性也对计算的精度产生了一定的影响。所以在掘进参数的选取时，尽量靠近开舱检查环数以及附近地层条件均一。经过比较，276～280 环满足上述条件。

中铁658 号所用的滚刀是由中铁装备生产的WIRTH 刀具，其具体参数如表1 所示。刀圈截面如图6。盾构在穿越276～280 环时，均是裕廊地层III 级，所以可以看成在此5 环内，岩石力学性质相同，即抗拉强度σc与抗压强度σt不变。272 环滚刀磨损量如图7 所示。在此期间，滚刀均属于正常磨损，即未发生偏磨现象，所以刀具的磨损情况如图8 所示。在刀圈发生磨损过后，会产生新的刀尖宽度T′以及刀刃角θ′，由于安装轴线并未发生变化，即滚刀间距S不变。由于中心滚刀发生磨损变化不大，磨损主要发生于离刀盘回转中心较远的地方，为了计算方便，本文取实际磨损量的平均值，即Δh=10mm。在此情况下，滚刀半径R=218.6mm，刀尖宽度T′=28mm，刀刃角θ′=26°。

表1 18寸滚刀基本参数

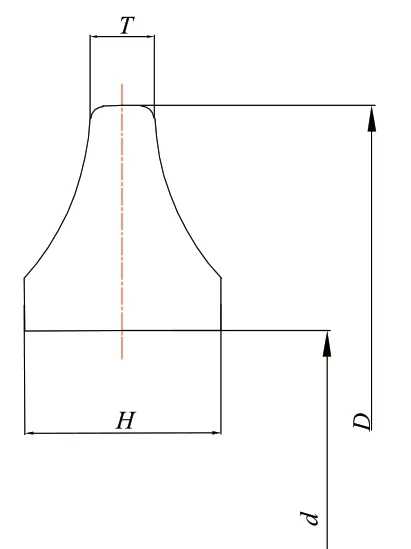
图6 刀圈截面图

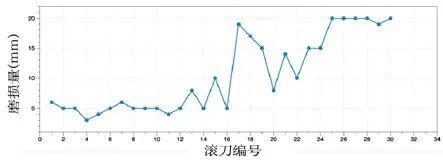
图7 272环滚刀磨损量

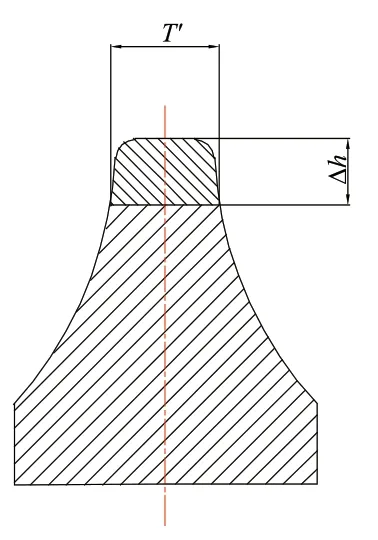
图8 刀具磨损

3.2 确定参数

通过查阅地质资料，在裕廊地层III 级时，岩石的抗拉强度主要从4～50MPa，最大硬度可达到165MPa，岩石内聚力c′=15kN/m2，有效内摩擦角为φ′=33°。可根据岩石的内聚力c′及有效内摩擦角φ两个参数绘制出σ-τ坐标下的库伦准则，即直线y=0.7x+0.05。由摩尔-库伦强度准则可知，当由σ1与σ3构成的应力圆与直线y=0.7x+0.05 相切时达到破坏的临界条件，所以可以找出σ1与σ3与之间的关系。即σ3=0.27σ1+0.05。因为岩石的抗拉强度主要分布在4～50MPa，小几率能够达到165MPa，所以在取岩石抗拉强度σc时，乘以放大系数λ以尽可能减小岩石强度对计算的影响程度，取λ=1.2。所以岩石的抗拉强度σc=60MPa。将其代入到σc与στ的关系式当中，得出στ=16.15MPa。

在刀具发生磨损的情况下，滚刀间距S未发生改变，滚刀半径R、刀尖宽度T及刀刃角θ均发生了变化。即R=218.6mm、T′=28mm、θ′=26°、S=100mm。

查阅地质资料，裕廊地层III 级时，CAI 指数为0.9，属于轻微磨蚀。由表2 可以查到石英砂岩和岩屑砂岩在自然状态、饱和状态、干燥状态3 种不同状态的静摩擦系数。由于裕廊地层属于沉积岩，所以选择在岩屑砂岩在自然状态下的数值，即μ=0.47。

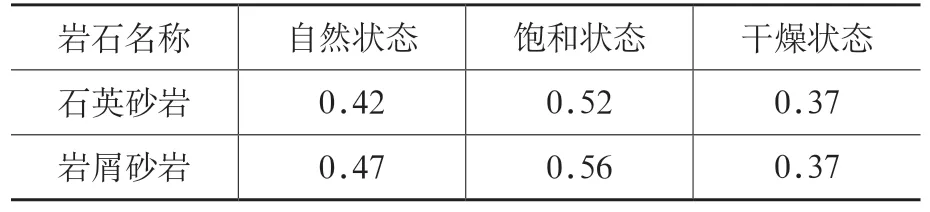
表2 岩石静摩擦系数μ

滚刀属于平刃型，所以刀尖压力分布系数ψ=0.1；在计算破碎区压力p0时用到的无量纲系数C=2.12；滚刀与岩石之间的摩擦因数μ=0.47。

3.3 CMS模型验证

由于现场条件有限，无法对滚刀的法向力Fv、切向力Fr及侧向力FN进行测量，所以在此引入比能，进行间接验证。

将切削单位体积岩石所消耗的能量定义为比能。可表示为

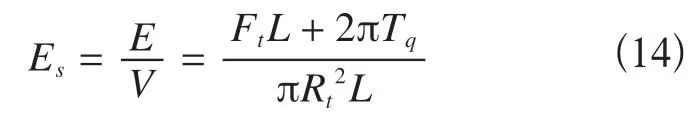
式中Es——刀盘比能；

E——刀盘单位周期所需要的能量；

V——岩石体积；

Ft——刀盘总推力；

Tq——刀盘总扭矩；

L——贯入度；

Rt——开挖隧道半径。

假定TBM 所有滚刀所受推力一致，则

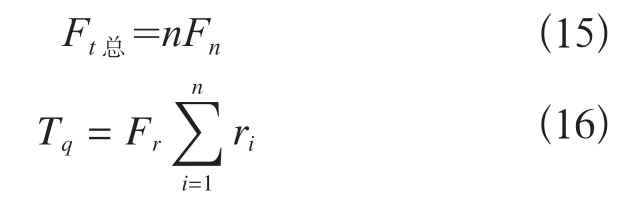
将式（10）代入至式（15）中，将式（13）代入至式（16）中，并将上述两式代入至式（14）中，得到式（17），即为经过修正后CSM 模型公式代入比能公式中所求的预测值。预测值与实际值比较如表3 和图9 所示。

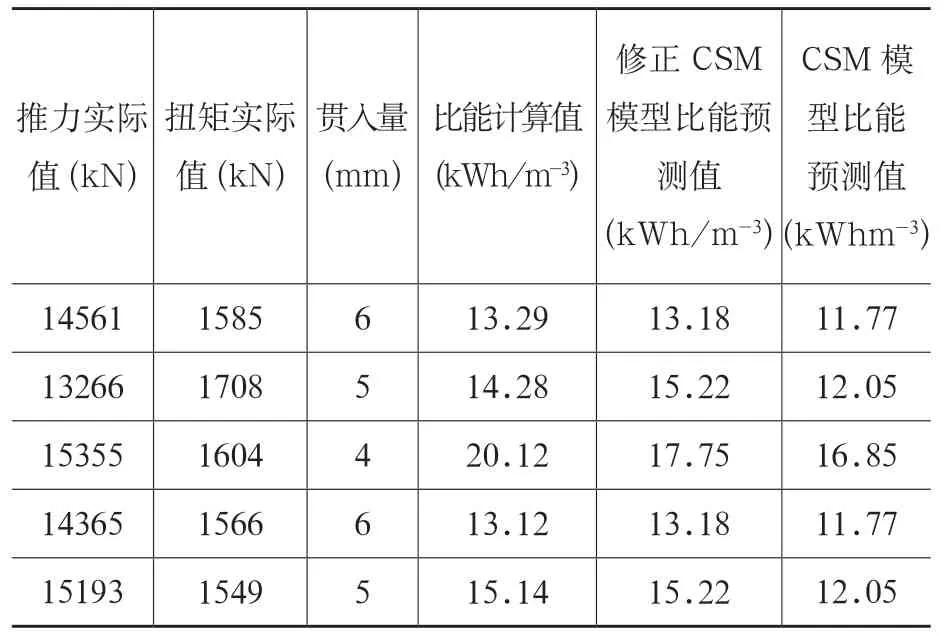
表3 276～280环比能预测值与实际值比较

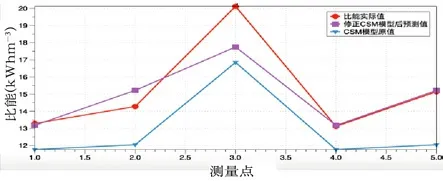
图9 比能实际值与修正值和原值比较

由图9 可看出，原CSM 模型的预测值与比能实际值相差较远，因为在计算扭矩时缺少因需要克服侧向压力而产生的摩擦力，因而导致计算普遍偏小。经过修正后的模型其预测值与实际值更加接近，且与实际值变化趋势保持一致，绝大多数的预测值是接近于实际值的，在278 环时偏小，可能是由于岩石分布不均与或是施工原因使得采集的推力或扭矩不准确导致的。

4 结论

本文是基于对CSM 模型深入研究，并对现有工程中刀圈磨损分析基础上提出的对CSM 模型的修正，并通过比能值对比原模型验证了其的可靠性。同时提出的刀圈不平衡力对刀圈磨损的预测有进一步的帮助。但是实际在实际工程中，通常是离回转中心远的滚刀磨损量大，且容易出现偏磨现象，因此今后在基于本文得出的一般性改进CSM 模型基础上有待更加深入的研究。