多性能强耦合分析技术及应用

王晓燕 郝文权 蒋永峰

（中国第一汽车股份有限公司 研发总院，长春 130013）

主题词：多学科 强耦合 分布式 算法

1 概述

多学科交叉耦合问题在车辆性能开发过程中变得越来越突出，采用多学科分析技术是提高车辆综合性能的必要手段[1-2]。传统的多学科分析是一种弱耦合技术[3-4]，不同学科之间只是简单的信息交互，没有求解器层面的耦合，因而难以完全表达不同学科之间的相互影响关系。此外，在车辆性能集成过程中，供应商出于对自身核心技术保护的角度考虑，不会把子模型以白箱的方式完全提供给主机厂，给整车性能集成带来困难。因此，需要探索一种强耦合算法，以实现不同学科在求解器层面的耦合，同时每个子模型仅需提供界面上的力与运动信息，实现“分而治之”的多学科强耦合分析[5]。

2 关键算法

如前所述，多学科强耦合分析算法只依赖于模型的接口信息，接口指的是两个模型的连接或共同的表面。接口可以用一组有限元模型中的接口节点或者一组多体动力学模型的铰链来表征。典型的接口信息分为运动信息和力信息。运动信息包括接口的位移、速度和加速度，力信息指的是接口传递的力与力矩。

耦合任何机械系统，力学原则要求接口处满足两组条件：

（1）力的大小，即接口力必须满足作用力与反作用力的平衡方程。

（2）接口处的运动量，必须要满足兼容条件。

如果定义好一组满足平衡条件的接口力变量，那么在耦合过程中只需要考虑运动量的兼容性条件。在这种情况下，接口力变量可以视为接口运动量的函数，并且这些接口力变量可以利用运动信息和兼容条件进行更新迭代。类似地，如果定义好一组合适的接口运动变量，即接口运动变量满足兼容性条件，那么在耦合过程中只需考虑接口力的平衡方程。在后者情况下，接口运动变量是接口力变量的函数，它们通过接口力的平衡条件来更新。两种不同的方式可以衍生出不同的耦合策略。

图1展示了T-T战略，以两个子系统的情况为例进行说明。在这个战略中，两个子系统模型的接口处的运动数量被用作耦合器的输入。两个模型的接口力向量和耦合器输出，将被用于子系统模型的下一步计算。

图2说明了X-T耦合战略。在这个方法中，两个模型的接口向量和被用作耦合器的输入。向量和是耦合器的输出（其中X代表位移，T代表力）。

图1 T-T方法

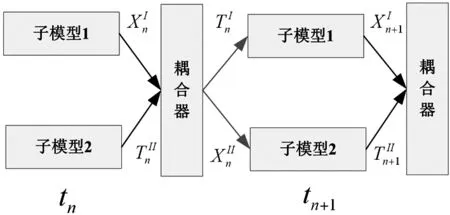
图2 X-T方法

下面以第二种情形为例阐述粘合算法的原理。

2.1 粘合算法[6][7]

假设X是合理定义的接口运动向量，其包含了必要和足够的变量能够代表接口的运动向量空间；F是合理定义的接口力向量，其包含了必要和足够的变量能够代表接口的力向量空间。并且X-T策略中接口位移X是自平衡，即如果接口处耦合输入信息是X，此接口自动满足位移兼容条件。e作为一个误差测量向量代表了接口力向量偏差，其中e=0表明接口力向量满足平衡条件。在通常情况，e可视为校正力变量Fc的函数，即

由于采用X-T耦合策略，运动向量自动满足兼容条件，那么粘合算法的唯一目标就是使得e等于零，即找到适当的Fc满足

方程（2）定义了一组（线性或非线性）方程，可以通过选择适当的算法（线性或非线性）方程求解器来解决。首先可以尝试使用拟牛顿法BFGS[8]进行求解，定义T接口校正力变量的初值为,其中yk是梯度差，Bk是Hesse矩阵。

然而工程绝大多数问题都是大规模、强非线性问题，BFGS算法虽然计算速度快，但是收敛上存在一定的鲁棒问题，因此需要研究更多高效稳定的迭代方法，例如LM+TrustRegion[9]方法：

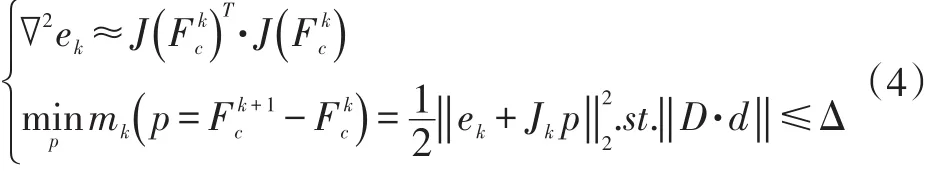
方程（3）以及方程（4）表明可以只利用接口的信息来获得适当的校正力Fc，使得接口满足力平衡条件。工程实践中，隐式算法首先使用BFGS算法进行初步计算，迭代过程中发现若不容易收敛，切换至LM+TrustRegion算法计算，这样既能保证收敛稳定性，同时又能提高计算速度。

2.2 延时预测计算方法

在多学科耦合过程中多体动力学计算与结构有限元计算存在一个时间步的延迟，迭代不易收敛或者不收敛，可采用近似模型技术进行预测解决此问题，具体算法步骤如下：

（1）对预测量的时间序列进行差分平稳化；

（2）建立时间序列分析模型；

（3）进行模型参数估计并验证模型；

（3）还原差分进行预测。

2.3 多学科强耦合算法在商业化软件中的实现

如前所述，多学科强耦合算法需要各子模型边界上的力与运动信息，在实际问题中，各子模型都是在各自的分析软件中求解，因此如何将多学科强耦合算法嵌入至商业化软件中，是首要解决的问题。比较理想的情况是直接针对商业化软件的内存进行操作来读取相应模型的信息，但这样涉及到各商业化软件的底层操作，需要商业化软件开放底层信息，实现起来工作量较大。本文在研究过程中，利用分析软件提供的程序外部接口，将每个子模型的仿真控制信息及计算结果进行存储，然后利用程序重新启动的命令来实现不同软件的信息传递及耦合。图3显示了ADAMS与ABAQUS联合分析的程序流程，在每一仿真步，ADAMS与ABAQUS分别对相应的子模型进行求解，并将子模型的仿真控制参数及结果信息保存至文本中。Mega-Solver粘合算法从结果文件中读取相应的边界运动信息，判断是否满足容差条件，如果满足，则进行下一步求解；如不满足，则根据迭代算法计算新的边界载荷向量，同时更新模型文件中相应的载荷信息，退回到当前步仿真起始点，调用当前步存储的模型控制参数文件，利用重启动命令重新进行当前步的分析。

图3 ADAMS与ABAQUS强耦合分析流程

3 多学科强耦合分布式分析技术[10][11]

多学科强耦合算法“分而治之”的建模思想，使得分布式建模的技术手段变得比较容易实现[12][13]，因为Mega-Solver粘合算法只需要子模型的边界信息，不需要模型的详细内部结构，因此可以在不同的客户机上仿真不同子模型的特性，将子模型的分析结构通过数据传输的方式传递给主机，在主机上运行多学科强耦合Mega-Solver的主程序，通过粘合算法将各子模型的边界信息进行耦合，再将粘合算法的计算结果传递给各子模型进行迭代求解，从而完成整个系统的耦合分析。

本文在研究过程中，建立了基于OPC技术的分布式仿真平台，如图4所示。基于多体与有限元耦合技术，利用MATLAB语言为主控机编写了控制代码，通过OPC服务器技术可以实现对客户机分配任务及传递客户机的计算结果；为客户机编写了计算控制代码，可以接受或等待主机分配计算任务并接受主机传递的计算结果数据，根据计算需要可以连接多台客户机。

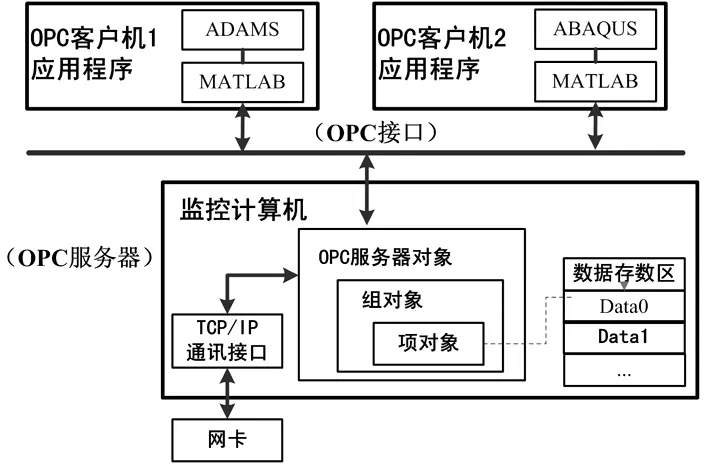
图4 基于OPC的多学科强耦合分布式分析技术

4 多学科强耦合分析案例

4.1 多体动力学耦合分析

根据前述多学科强耦合算法原理，考虑多体动力学耦合分析案例。如图5所示，在ADAMS中，将一根杆的一端用衬套固定在大地上，另一端加正弦激励。将杆从中间一分为二，边界节点用物体局部Marker表示，拥有6个自由度；节点之间的相互作用力通过广义力作用在物体I和物体II上。两个子模型分别在AD⁃AMS中进行求解，利用耦合算法进行耦合求解。

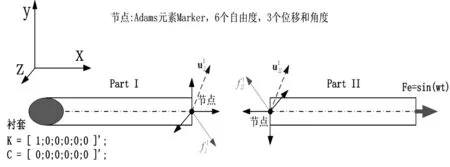
图5 多体动力学强耦合分析案例

图6 为耦合求解结果与ADAMS整体求解结果的对比，从图中可以看出，耦合算法较精确地模拟了整体系统的运动。

4.2 多体动力学与有限元联合分析

为验证Mega-Solver算法的分析精度，采用简易的钢板弹簧结构，其两端的链接方式如图7所示，在梁的中间施加载荷。传统的ADAMSFlex在分析过程中，采用模态叠加的方法，因此在大变形、非线性区时模型的误差较大，通过多学科强耦合联合分析技术，可以直接耦合ADAMS的动力学分析模型与板簧的有限元模型，因而分析精度大幅提升，图8为采用Mega-Solver耦合算法、ADAMSFlex及有限元算法的精度对比，可以看出，采用耦合算法后，分析结构与有限元的分析精度基本吻合，而ADAMSFlex在大变形时与有限元的计算结果偏差较大。

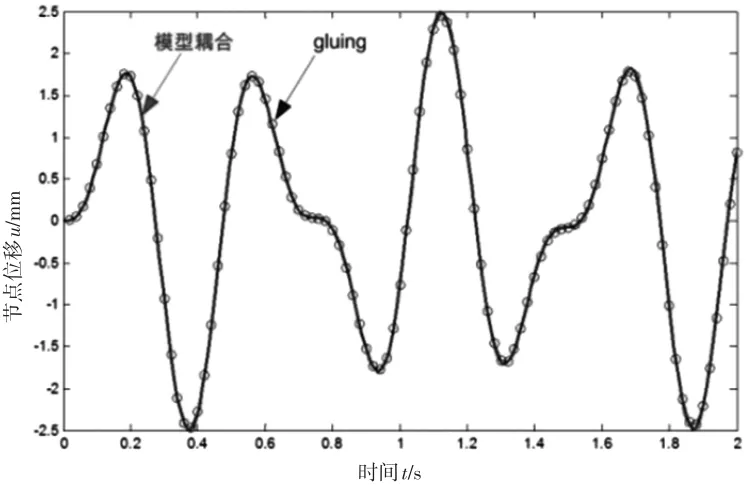
图6 多体动力学耦合案例仿真结果

图7 多体动力学与有限元耦合分析案例

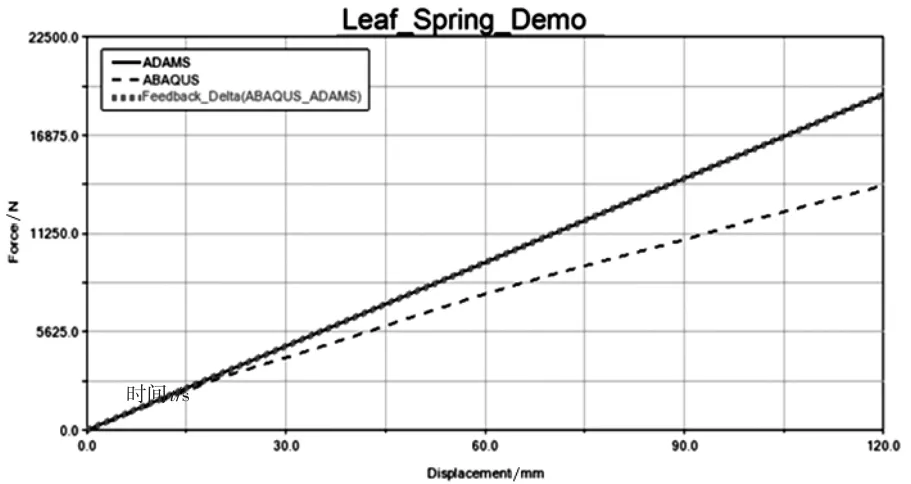
图8 多体动力学与有限元耦合结果

4.3 整车耦合分析

利用多学科强耦合分析技术实现了整车的耦合分析建模，其中底盘系统利用动力学软件求解，如图9所示，车身在有限元中进行求解，如图10所示。每一计算步，底盘与车身在连接点处进行力与运动信息的交换，通过粘合算法进行综合求解。

5 结论

利用多学科强耦合Mega-Solver算法，可以实现多学科、多软件的强耦合分析。Mega-Solver算法只需要界面的力与运动信息，而不必关注各子模型的内部详细结构，从而可以进行分层模块化的建模及分析工作。由于模型的模块化处理，可以通过分布式技术实现子模型的同步求解，大大提高了分析的效率；同时，由于Mega-Solver本质上实现了求解器之间的耦合分析，可以充分发挥不同求解器的优势，在处理强非线性、接触等问题时可以进一步提升分析精度。

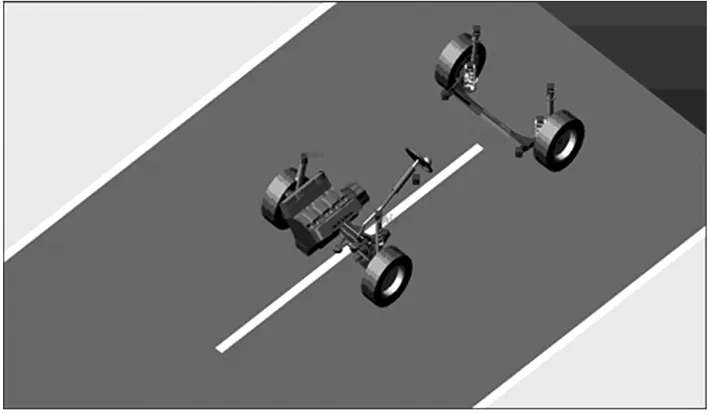
图9 耦合分析底盘子模型

目前，Mega-Solver粘合算法的稳定性仍有待进一步研究，通过引入多种迭代方法相结合以及多步法等技术手段，提高算法的鲁棒性。