考虑岩体自重的下伏溶洞岩石地基冲切分析

刘泽宇，雷 勇，邓加政，刘一新，谭 豪

(1. 湖南科技大学 岩土工程稳定控制与健康监测湖南省重点实验室，湖南 湘潭 411201；2.广东中科华大工程技术检测有限公司，广东 广州 511458)

0 引言

为实现全面建成小康社会的目标，近年来我国基础建设向地质条件更为复杂的西南地区延伸。由于西南地区广泛存在的岩溶地质条件，桥梁桩基穿越或置于溶洞岩石地基之上难以避免。一般认为当溶洞顶板岩体质量较好且超过一定厚度时，顶板尚具有一定的承载力，可将桩基置于溶洞顶板之上。这种设计既可节约桥梁建设成本，同时大大降低桩基的施工难度。故此众多学者对下伏溶洞岩石地基极限承载力问题开展了广泛研究。

张慧乐等[1-2]通过室内模型试验，揭示了顶板厚度、荷载偏移等因素对下伏溶洞桩基桩端承载力的影响规律。胡庆国等[3]、李仁江等[4]运用数值分析软件对影响下伏溶洞顶板极限承载力因素进行了分析，研究表明：顶板跨度、顶板厚度及溶洞形状对地基极限承载力影响较大。刘之葵等[5]利用弹性理论分析了含溶洞的岩石地基稳定性。雷勇等[6]基于极限分析法结合H-B准则研究了顶板厚度、GSI等因素对下伏溶洞岩石地基极限承载力的影响，而后[7]基于溶洞顶板的冲切破坏模式得到了冲切体的底部直径和三维下伏溶洞岩石地基极限承载力显示公式。刘一新等[8]从极限分析上限法出发引入Hoek-Brown准则，得到了非对称荷载下下伏溶洞岩石地基极限承载力计算方法。

上述研究加深了对下伏溶洞岩石地基的承载机理的认识，然而上述研究都未考虑自重对极限承载力的影响，有关自重对下伏溶洞地基极限承载力影响研究较少且不充分。

柏华军[9]在采用极限平衡法计算溶洞顶板安全厚度时考虑了岩体自重，但其表达式较为复杂，未对不考虑自重和考虑自重时溶洞顶板的安全厚度进行比较。李亮[10]、曾中林[11]等采用两种不同非线性准则研究了二维状态下的下伏溶洞岩石地基极限承载力，虽然在求解过程中考虑了自重因素但未指明自重对于下伏岩石溶洞地基极限承载力的具体影响。YANG X L[12]和严若明[13]等同样采用极限分析法研究了隧道垮塌机制，研究表明：在岩体质量较差的情况下岩体自重可致使溶洞顶板发生垮塌或坍塌。换言之，当岩体质量较差时下伏溶洞岩石地基有可能承载力极小或无法承载上部结构的附加荷载。由于实际工程中岩溶区岩体质量存在的缺陷，因而研究考虑自重时不同岩体质量情况下下伏溶洞地基极限承载力变化规律更能安全地评估下伏溶洞岩石地基的承载力。

针对上述下伏溶洞岩石地基承载力研究中对岩体自重考虑的不足，在前人研究基础上，本研究基于极限分析上限法[14]，建立了考虑自重下下伏溶洞地基极限承载力的三维功能方程，推导出冲切体母线方程及下伏溶洞岩石地基极限承载力表达式，并通过室内模型试验进行了验证。最后编程分析了自重对下伏溶洞岩石地基极限承载力及溶洞临界跨径的影响，以期为岩溶区基础工程设计提供参考。

1 Hoek-Brown强度准则

目前Hoek-Brown准则广泛应用在岩体工程中，为适应不同的研究需要，一些学者将Hoek-Brown强度准则[15]的应力形式用其他参数表示，其中A.Serrano等[16]采用岩体瞬时摩擦角ρ表示的Hoek-Brown强度准则得到了广泛的应用。为便于分析本研究选取无量纲应力，其破坏面上的切向应力和法向应力分别为：

(1)

(2)

(3)

(4)

式中，σn，τn分别为岩体破坏面上的法向应力、剪应力；β为强度模数；ζ为抗拉强度系数；RMR为岩体地质力学分类指标；σc为完整岩块无侧限抗压强度;m0为岩体类型参数。

(5)

式中，A，B两参数可由拟合求解，其取值与研究目标应力范围相关。文献[6]与文献[16]分别给出了高应力与低应力条件下A，B的值。

联立式(2)、(5)可解得τ*的表达式为：

(6)

2 溶洞地基极限承载力上限分析

2.1 基本假定

一种合理的破坏机制是求得下伏溶洞岩石地基极限承载力上限解的必要条件。雷勇[17]等通过试验研究证实：溶洞岩石地基冲切破坏体是一个以曲线为母线的对称旋转体而非标准的圆锥台形。基于前人[18-20]的研究及极限分析相关联准则的要求和溶洞顶板冲切破坏的特点，假定下伏溶洞岩石地基破坏模式如图1所示。并做如下假设：

(1)荷载为中心荷载，溶洞顶板厚度为h溶洞跨径足够大，发生的都为自由冲切破坏；

(2)当作用在顶板上的荷载值到达极限承载力时，冲切体由破坏面内部和外部两个刚性区、破坏面周围的塑性区3部分组成。δ表示塑性区的厚度当发生塑性破坏时符合相关的流动法则；

(3)岩体的破坏机制符合Hoek-Brown准则且为性质均一的理想刚塑性材料。

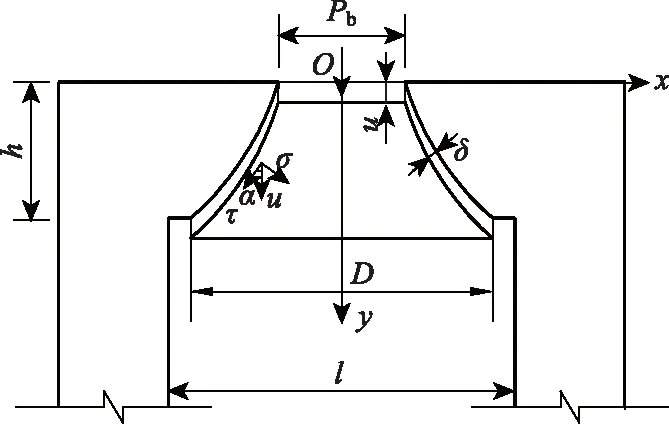
图1 冲切体破坏模式

2.2 冲切体破坏面功能方程的建立

下伏溶洞岩石地基极限承载力的求解关键在于利用外荷载所作功率与外部损耗率功率相等[14]。即：

(7)

外荷载所做功率：

(8)

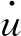
破坏体在自重应力作用下所做功率：

(9)

式中，d，D分别为冲切破坏体上下直径；l为溶洞跨径；x为其任意h时的半径；f(x)为冲切体母线方程；γ为重度。

当塑性区发生破坏时，内能损耗率为：

(10)

其中：

(11)

(12)

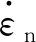
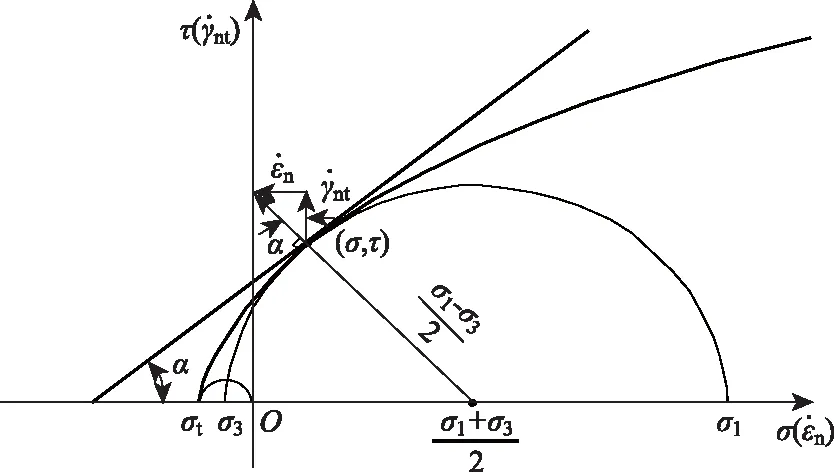
图2 Hoek-Brown强度准则剪应力(应变)形式

由图2可知应变率和运动速率的关系可表示为：

(13)

(14)

若材料服从关联流动法则及Hoek-Brown准则，其塑性势可表达成下式：

(15)

可由式(15)求得相应的塑性应变率：

(16)

(17)

式中λ>0为比例系数。

由式(1)、(2)、(6)和式(13)～式(17)可得：

σn=β[ABf′(x)]1/(1-B)-βζ，

(18)

τn=Aβ{[ABf′(x)]1/(1-B)}B。

(19)

塑性区发生塑性破坏时，其单位体积内能损耗率可由式(18)和式(19)代入式(12)中求得：

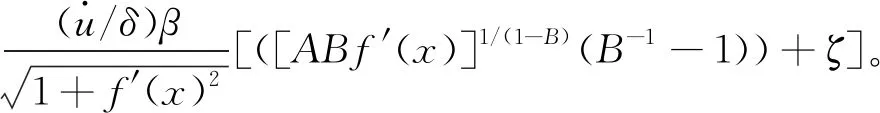
(20)

将式(11)和式(20)代入式(10)可得：

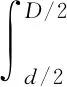
(21)

联立式(7)～式(9)和式(21)整理可得：

γxf(x)}dx-πD2hγ。

(22)

由于式(22)中含有f′(x)，f(x)和x，其实质为求解泛函的极值问题，可通过变分法求解。

2.3 溶洞岩石地基极限承载力的求解

运用变分原理求解式(22)极值，首先定义：

F[f(x)，f′(x)，x]=[(ABβf′(x))1/(1-B)(B-1-1)+

βζ]x+γxf(x)。

(23)

根据欧拉方程：

(24)

将式(23)代入式(24)进一步解得：

(25)

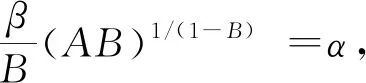
(26)

(27)

(28)

对式(28)求解得：

(29)

式中C1为待定系数。

由f′(x)，t，w和x的关系可以得到：

(30)

对式(30)进行积分可以得到冲切体的母线方程，将其代入式(22)即可求解得到考虑自重的下伏溶洞岩石地基极限承载力表达式。由于式 (30)较为特殊，仅当(1-B)/B为整数时才能积分，否则母线方程和溶洞岩石地基极限承载力表达式无法显式求得。

为求得任意参数下的溶洞岩石地基极限承载力，可采用差分法对冲切体母线的函数f(x)进行求解。原理为将母线函数在二维坐标系中分解为若干微段，根据积分原理知可由直线替代微段。结合边界条件，逐段积分求和，得到不同参数B下的冲切体母线函数。而后积分迭加可求得溶洞岩石地基极限承载力Pb。

差分法基本原理：

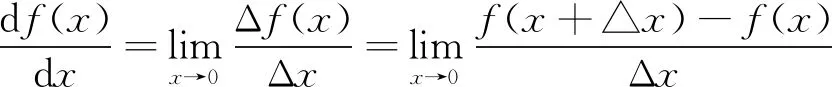
(31)

给定式(30)中参数C1，γ，A,B和β，可求得任意xi的导数值。由微积分知识知任意一段曲线可划分成无数微段直线，假定每一微段为xi+1-xi=Δx，则将每点的导数值可视两相邻点函数值连接直线的斜率。根据式(31)可得：

Δf(xi)=Δxf′(xi)。

(32)

将式(32)迭加计算，可求任一点的f(xi+1)值，其表达式为：

f(xi+1)=f(xi)+Δf(xi)。

(33)

由于无法得到该曲线的精确解析解，因此可用同样的方法推导出溶洞岩石地基极限承载力Pb。每一微段直线对应的薄层极限承载力Pb(i)的积分表达式：

(34)

于是整个溶洞地基极限承载力Pb的表达式为：

Pb=∑Pb(i)-πD2hγ。

(35)

基于上述推导过程，利用数学软件Matlab进行编程，可得到Hoek-Brown准则下任意参数组合的溶洞岩石地基极限承载力Pb具体表达式及冲切体母线函数。

选取B=0.5进行分析，B=0.5时,式(30)：

(36)

(37)

(38)

式中,C1，C2为待求参数，可由边界条件f(d/2)=0，f(D/2)=h确定，其中D为冲切体底部直径，也是满足假设条件的临界跨径，求得各参数的表达式为：

(39)

(40)

可得：

(41)

将式(41)代入式(22)得到极限承载力Pb为：

(42)

当式(42)中γ=0时便可退化为不考虑自重的溶洞地基极限承载力Pb，其表达式为：

(43)

式(43)中只有冲切体底部直径D为未知数，可运用数学上常用求解极值方法进行求解。首先对D求偏导并令偏导数为0，此时得到的D对应于冲切体底部直径。将所求解D代入极限承载力函数中，便可求得溶洞岩石地基极限承载力Pb。可求得底部冲切体直径D具体表达式为：

(44)

式中，LambertW为朗伯函数，具体应用参见文献[21]。

2.4 极限承载力求解过程

当考虑自重时，无法用∂P/∂D=0求得D的具体显式表达式，进而无法求解出溶洞岩石地基极限承载力。为求解溶洞顶板承载力极值及冲切体底部直径D，给出求解过程如图3所示。

图3 极限承载力求解流程图

3 试验验证

3.1 模型试验

为验证理论方法的合理性，进行了下伏溶洞岩石地基及基岩极限承载力室内模型试验。溶洞基岩由水泥、石膏、砂和黏土按一定比例配制。溶洞直径l=33 cm，拱高15 cm，分别进行顶板厚度为1d，2d，3d的小型荷载板试验，以及相应的基岩极限承载力试验，其中d=5.75 cm。通过试验测得基岩试块单轴抗压强度为2.97 MPa，内摩擦角φ=30°。试验加载系统及模型试验如图4所示。

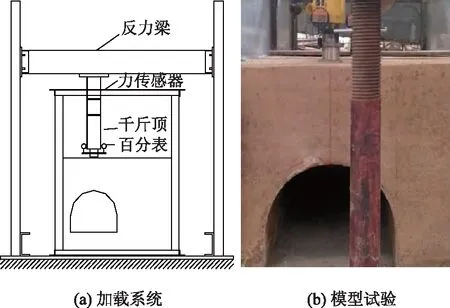
图4 加载系统及模型试验

按采用的配比材料的性质及完整性，采用Hoek-Brown强度准则时，相关计算参数及实测岩体材料参数取值按以下原则[22]：因为为室内试验，可认为无节理，RMR可取值100，m0取7.0，然后将其代入式(3)和式(4)可得β为2.6，ζ为0.16。拟合参数A取值为0.52，其他参数取值见表1。

3.2 极限承载力

根据实测的荷载-位移曲线关系，得到溶洞顶板厚度为1d，2d，3d和4d时，溶洞顶板的极限荷载分别为10，28，40和60 kN，且顶板都发生冲切破坏。由式(42)和式(43)计算的理论值极为接近，其原因是室内模型试验岩体比较完整，冲切破坏面抗力较大，且冲切体自重相较冲切荷载可忽略不计。理论计算结果与实测值对比曲线如图5所示。

表1 相关计算参数

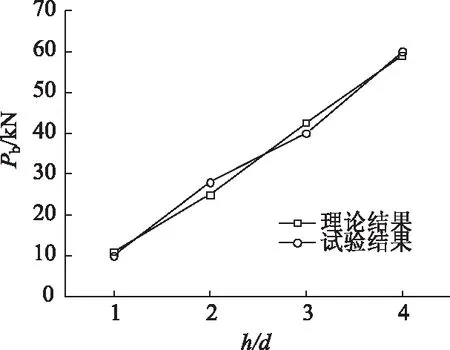
图5 Pb的理论值与实测值对比曲线

由图5的对比曲线可知按式(42)、(43)计算的理论结果是合理的，能够运用于溶洞岩石地基的极限承载力计算。

然而由于实际工程中岩溶岩体质量并不好，且完整程度也不如室内模型材料理想，因此可以开展参数分析，以获得实际工程岩体中岩体自重对下伏溶洞岩石地基承载力及相关参数的影响。

4 参数分析与对比验证

4.1 参数分析及取值

由式(42)可知改变拟合系数A、拟合系数B、岩体地质力学分类指标RMR、岩体重度γ及岩体的单轴抗压强度σc中任一参数，溶洞地基极限承载力会随之改变。文献[23]建议化学沉积岩类的m0取值范围为3～15，本研究岩体类型参数m0取7.0，A取0.88、B为0.5。相关分析参数的取值范围见表2。

表2 相关分析参数范围

4.2 自重γ和岩石单轴抗压强度σc对Pb的影响

本节对考虑自重γ和岩石单轴抗压强度σc对溶洞岩石地基极限承载力进行研究。溶洞顶板厚度h取1d，不同岩石单轴抗压强度σc下溶洞地基极限承载力随RMR值变化规律如图6所示。由图6可知岩石单轴抗压强度σc,RMR对极限承载力的影响规律与是否考虑自重一致。当岩体其他参数相同时，随着RMR值的增加,溶洞岩石地基极限承力呈非线性增长；岩石单轴抗压强度σc愈高溶洞岩石地基极限承载力愈强。但二者都随着自重γ增加溶洞地基极限承载力Pb减小，变化并不明显。当RMR值和岩石单轴抗压强度σc均较小时，溶洞岩石地基极限承力极小，接近于0。该现象说明岩体质量较差和强度较低时，溶洞岩石地基不具备承载能力，甚至可能坍塌。

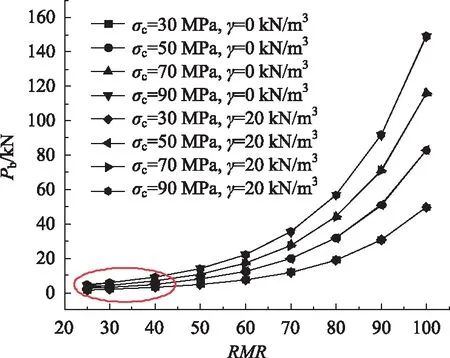
图6 RMR和σc对极限承载力的影响

4.3 自重γ和顶板厚度h对Pb的影响

根据文献[24]对RMR值大小的分级，可将岩体质量分为5个等级。选取RMR为40(差岩体)、60(一般岩体)、80(好岩体)、100(非常好)4个值分析当单轴抗压强度σc为70 MPa且不同顶板厚度下的溶洞岩石地基极限承载力Pb。根据式(42)和(43)计算的不同顶板厚度下的溶洞岩石地基极限承载力值绘成如图7所示。

图7 顶板厚度对Pb的影响

图7表明：随着溶洞顶板厚度h的增加溶洞岩石地基极限承载力Pb基本呈线性增加；当考虑岩体自重γ，顶板厚度h为3d且RMR<40时溶洞岩石地基极限承载力为负值。该现象说明考虑自重时，岩体质量较差和顶板厚度较大时的溶洞岩石地基不具备承载能力。

结合公式(42)和图7分析可知岩体质量等级为差岩体及以下岩体时(RMR<40)，当顶板厚度增加时其内能耗散功率增量小于重力功率增量,因此出现随顶板厚度增加溶洞出现自然垮塌现象。岩体质量等级为一般岩体及以上岩体时(RMR>60)，随着顶板厚度增加内能耗散功率增量大于重力功率增量且内能耗散功率增量较快故溶洞岩石地基极限承载力增加。

4.4 自重γ对溶洞临界跨径D的影响

本研究采用编程计算出是否考虑自重下的溶洞临界跨径，二者差值见图8。由式(44)可知，岩石单轴抗压强度σc对未考虑自重的溶洞临界跨径无影响，因此针对不考虑岩体自重时的溶洞临界跨径D只选取单轴抗压强度σc=70 MPa、γ=0与考虑岩体自重时的溶洞临界跨径D进行对比分析。对比分析图如图8所示。

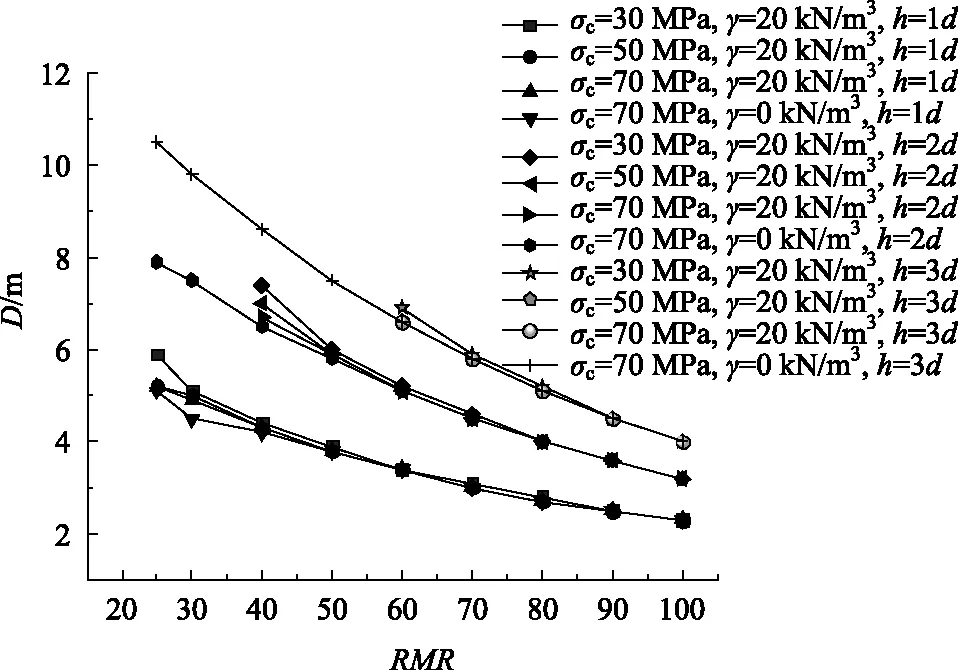
图8 自重对溶洞临界洞径的影响

由图8可见：RMR和溶洞顶板厚度h对溶洞临界跨径D影响较大。考虑自重时，当RMR<40且顶板厚度h>2d的情况下，Pb计算值为负值，此时会出现溶洞顶板发生自然垮塌，D的取值不是明确意义上的溶洞顶板冲切跨径；当RMR>60单轴抗压强度和自重对溶洞临界跨径影响值较小，考虑自重与否的溶洞临界跨径二者差值在3%以内；当RMR>90时，二者溶洞临界跨径取值一致。

4.5 考虑自重时γ的Pb

表3给出了是否考虑自重、不同溶洞顶板厚度h及单轴抗压强度σc下溶洞岩石地基极限承载力随RMR变化情况。表3数据显示：当RMR≤40时计算溶洞岩石地基极限承载力是否考虑自重γ差值较大。在h=1d及岩石单轴抗压强度σc=30 MPa时差值最大可达到11.11%。在h>2d时考虑溶洞自重时，Pb的计算值会出现负值，溶洞顶板出现垮塌。而不考虑自重则溶洞顶板均具有一定极限承载力，且不会发生溶洞顶板坍塌。故在实际工程中RMR≤40时，需要考虑自重对极限承载力的影响，偏于安全；当RMR≥60时，即对于一般级别以上的岩体(中风化、微风化、未风化)计算溶洞地基极限承载力时是否考虑自重的误差在3%以内。

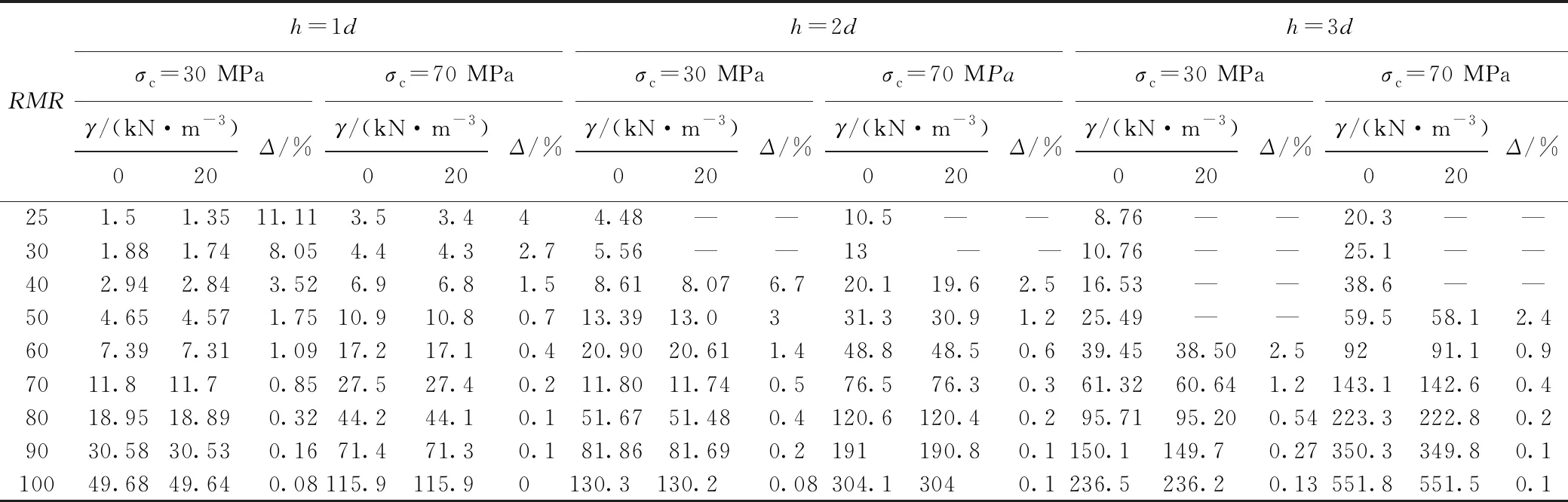
表3 不同工况下考虑自重与否的极限承载力(单位：kN)

5 结论

本研究构建了考虑自重的冲切体三维功能方程，并通过编程得到了自重对溶洞岩石极限承载力等因素的影响，得到如下结论：

(1)岩石RMR值、单轴抗压强度对溶洞岩石地基极限承载力影响规律与是否考虑自重因素无关，均随着单轴抗压强度σc和RMR值增加而提高，反之亦然。二者均随着自重增加溶洞岩石地基极限承载力减小，但变化并不明显。当RMR值和岩石单轴抗压强度σc均较小时，溶洞岩石地基极限承力极小，接近与0。该现象说明岩体质量较差和强度较低时，溶洞岩石地基不具备承载能力，甚至可能坍塌。

(2)随着溶洞顶板厚度h的增加溶洞岩石地基极限承载力Pb基本呈线性增加；当考虑岩体自重γ，顶板厚度h为3d且RMR<40时溶洞岩石地基极限承载力为负值。该现象说明考虑自重时，岩体质量较差和顶板厚度较大时的溶洞岩石地基不具备承载能力。当考虑自重和顶板厚度时，溶洞岩石地基极限承载力的变化主要取决于内能耗散功率增量与重力功率增量之间的差值。当内能耗散功率增量大于重力功率增量时溶洞岩石地基极限承载力增加，当内能耗散功率增量小于重力功率增量溶洞岩石地基极限承载力减小。

(3) 当RMR<40时自重对溶洞临界跨径影响较大，当顶板厚度h>2d时会出现自然垮塌；当RMR>60时单轴抗压强度和自重对溶洞临界跨径影响值较小，考虑自重与否的溶洞临界跨径二者差值在3%以内；当RMR>90时，二者溶洞临界跨径取值一致。

(4)实际工程中RMR≤40时，需要考虑自重对极限承载力的影响；当RMR≥60时，计算溶洞岩石地基极限承载力时是否考虑自重其值差别较小一般在3%以内。