吊脚桩基坑支护设计——以山东临沂市中汇大厦基坑为例

王文跃，李静，吕海滨，刘世强，马明强

（山东正元建设工程有限责任公司，山东 济南 250101）

0 引言

二元岩土结构的基坑支护常采用吊脚桩+锚索支护结构，对这种支护结构还没有统一的计算模式。目前学者主要依据古典法、弹性地基梁法和连续介质有限元法（刘国彬和王卫东，2009）基本理论进行研究。

数值法软件主要有：ANSYS、FLAC、ABAQUS、PLAXIS、同济曙光GeoFBA（郑颖人等，2012），目前中国学者主要采用以上软件进行理论分析与研究，基坑设计的软件有限元法取得的主要进展：刘红军等（2008）首先研究了吊脚桩嵌岩深度、岩肩宽度对变形的影响，指出增加嵌岩深度、岩肩宽度，位移与正弯矩明显减小，对其研究对象提出岩肩宽度超过1.4 m、嵌岩深度超过3.0 m，其影响将不大，嵌岩深度和锚杆轴力可以相互补充；李东（2009）研究了二元地层结构土压力分布规律并给出了计算方法，验证了吊脚桩的合理性；刘红军等（2009）模拟和分析吊脚桩岩肩宽度、嵌岩深度、锁脚锚杆预应力等因素对基坑变形和稳定的影响，指出嵌岩深度和锚杆预应力都能有效控制基坑的变形和稳定，锚杆预应力为主要控制因素；袁海洋等（2013）研究了吊脚桩刚度对桩顶位移的影响，指出增大刚度对减小变形有明显的作用，刚度到一定程度后减小变形不再明显；随后一些学者对四个主要因素进行了深入的研究：迟建平（2014）的研究表明桩径、嵌岩深度、岩肩宽度、锁脚锚杆预应力对吊脚桩的水平位移影响敏感性依次降低（迟建平，2014）；平扬等（2014）研究了锁脚锚索倾角与变形的关系，提出倾角锚固效果顺序为20°＞25°＞15°；田海光（2015）的研究表明锁脚锚杆预应力对桩底水平位移控制作用明显，随嵌岩深度、岩肩宽度的增加桩身最大水平位移呈减小趋势，嵌岩深度取2.0 m，岩肩宽度取1.5 m 较合理；吴晓刚（2016）研究了吊脚桩桩侧位移与地表位移的规律，开挖至基坑时，侧位移呈花瓶形，地表呈凹槽型；武军等（2018）的研究表明随着基坑开挖桩身最大位移下移而内力也随之增加到最大值，并提出岩石岩性模量600～4800 MPa 之间，最优设计嵌岩深度为1.5 m，最优设计岩肩宽度为1.5～2.0 m；杨俊辉（2019）研究后认为增大嵌岩深度、岩肩宽度、锁脚锚杆预应力有利于减小基坑变形，但超过某一值后，作用不再明显；吴会军等（2019）分析与嵌岩深度、岩肩宽度锁脚锚杆预应力对桩身水平位移的敏感度分别为0.45，0.28，0.20，对桩脚水平位移的敏感度分别为0.57，0.48，1.08。此外，岳建国和齐云龙（2016）采用三维有限元法研究吊脚桩的可行性。综合以上结果：（1）桩径、嵌岩深度、岩肩宽度、锁脚锚杆预应力对控制桩身位移均有控制作用，但各自所起作用的大小有差异；（2）桩径、嵌岩深度、岩肩宽度超过某一值后，对吊脚桩变形、内力影响不再显著；（3）桩身位移主要在土层中，呈上大下小趋势，锚索布设结构影响桩身位移特征；（4）对一定强度的岩石，各自提出了不同的嵌岩深度、岩肩宽度建议值。有限元理论研究为吊脚桩简化设计提供基础性认识，但设计复杂。

在古典法与弹性地基梁法取得的进展：设计两步进行，岩石面以上采用弹性地基梁法或古典法，岩石面以下按岩石边坡设计。大量的工程实践是在具有一定嵌岩深度和岩肩宽度条件下直接采用支护软件验算支护结构的稳定性，依靠经验来确定锁脚锚杆的预应力（邓春海等，2011；朱丹辉，2014；马文旭和刘雄华，2015；黄薛等，2019）；一些学者采用理正软件设定小的嵌岩深度以满足软件计算模式，通过调整计算工况来施加锁脚锚杆预应力（徐涛和张明强，2012；韩国俊和刘洋，2013；毕经东和张自光，2013）。许岩剑等（2015）认为吊脚桩支护型式基坑深度在岩石面时属于桩锚支护型式，基坑深度超过桩底标高后支护型转变为锚杆竖肋结构，应按2 种状态设计要求综合设计。李宁宁在岩肩宽度为1.2 m 条件下对不同嵌岩深度、锚索预应力对支护体系的影响进行分析后，指出理论上嵌岩深度0.5 m 是可以的，但考虑到挖坑影响，建议嵌岩深度取1.0～1.5 m；锚索作用主要是锁住桩脚，对支护体系整体稳定有较好的作用。显然，采用弹性支点法更适合工程实践。

对于吊脚桩支护结构，嵌岩深度要求达到0.5 m 以上易于保证，但岩肩宽度往往受场地限制而不能保证。对于岩肩宽度不足1.2 m 或没有岩肩宽度的情况下，吊脚桩支护设计方法少见报道。该文探讨的方法且称为迹线法，基本路径是：先试算寻找合理的嵌固深度，采取土反力合力对顶层支点求作用力矩；在基岩面以上设置锁脚等效支锚，以等效支锚力对顶层支点求抗力力矩，求出等效支锚力标准值。以下以山东省临沂市中汇大厦基坑为例说明论述。

1 嵌固深度对支护桩性状影响

1.1 参数选用

为便于探讨，以工程实例岩土参数作为分析参数。岩土参数见表1，锚索参数见表2。

支护桩直径为800 mm，桩顶标高-3.0 m；冠梁高0.6 m，宽1.0 m；荷载一：均布荷载20 kPa，荷载二：条形荷载100 kPa，作用宽度15 m，作用深度1.5 m，距坑边距6.5 m，地下水深度按21 m 取值，基坑开挖深度按9.6 m 取值；基坑安全等级一级。支护结构简图见图1。

表1 岩土参数表

表2 锚索参数表

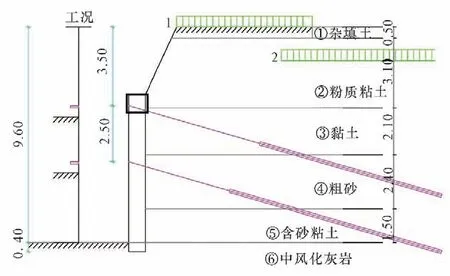
图1 基坑支护剖面示意图

1.2 支护桩位移曲线与弯矩曲线特征

采用理正7.0 版软件计算，在以上参数不变，嵌岩深度hd取值0.40～7.50 m，基坑开挖至岩土界面（9.60 m），支护桩位移与弯矩呈阶段性特征。

（1）嵌岩深度hd≤0.40 m，位移曲线近似直线，桩端连线坑内倾斜，桩底抗力不足；负弯矩极值较小，岩面以下正弯矩为0；嵌岩段土反力合力大于被动土压力合力，支护桩踢脚失稳。桩端为不稳定自由端，hd≤0.4 m 为不稳定自由端区域。位移、弯矩曲线图见图2。

（2）嵌岩深度0.50 m≤hd＜1.45 m，位移曲线呈C 形，位移极大值点持续上移至顶层支锚点，桩端连线坑内倾斜—垂直—坑外倾斜变化，桩底抗力与桩顶抗力关系为：小于—等于—大于变化；负弯矩极值持续增大，岩面以下正弯矩值为0；嵌岩段土反力合力越来越小，且小于被动土压力合力，桩端稳定。桩端为稳定自由端，0.50 m≤hd＜1.45 m 为稳定自由端区域。位移、弯矩曲线图见图3。

（3）嵌岩深度1.45 m≤hd≤1.65 m，位移曲线C 形，位移极大值点在顶层支锚点，坑底面以下近似直线，桩端连线坑外倾斜，桩底端位移为0.0 mm，误差±0.3 mm；负弯矩极值抵近最大值333.0 kN·m，误差±0.5 kN·m。嵌岩段土反力合力抵近最小值246.0 kN/m，误差±2 kN/m，且小于被动土压力合力，桩端稳定。桩端铰接，1.45 m≤hd≤1.65 m 为铰接端区域。位移、弯矩曲线图见图4。

（4）嵌岩深度1.65 m＜hd≤7.5 m，位移曲线C形渐变S 形，桩端连线坑外倾斜，随着深度的增加，坑底面以下有1 mm 左右反向位移，到一定深度，出现假象0.07 mm 位移偏移，桩底端一定长度为零位移；负弯矩极值继续减小，到一定深度，负弯矩基本保持不变，坑底面出现明显的正弯矩；嵌岩段土反力合力反转增大，且远小于被动土压力，桩端稳定。桩端固接，可以认为1.65 m＜hd为桩端固接端区域。位移、弯矩曲线图见图5。

图2～5 曲线反映：嵌岩深度不足时，支护桩踢脚失稳；嵌岩深度达到某一值域时（如本例的1.45～1.65 m），桩底位移为0.0 mm，负弯矩极值为最大值，土反力合力为最小值。嵌岩超过该值域，桩端为固接模式，再增大嵌岩深度都是徒劳的。

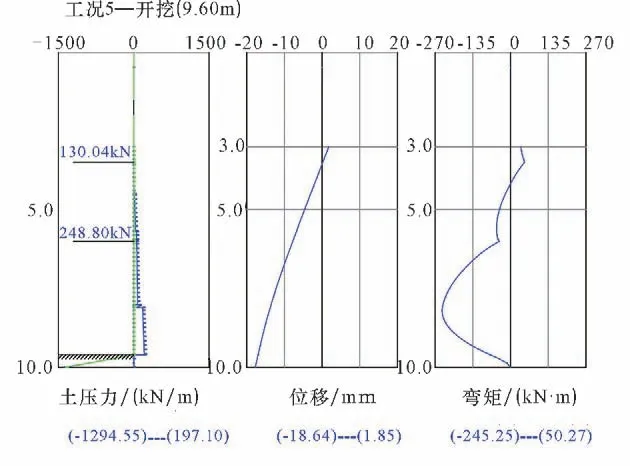
图2 嵌岩深度0.40 m 时位移、弯矩曲线

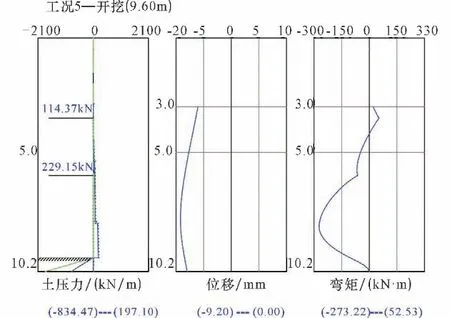
图3 嵌岩深度0.6 m 时位移、弯矩曲线

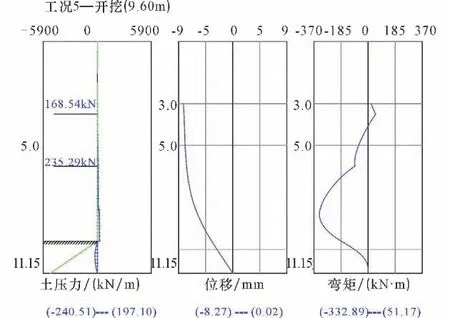
图4 嵌岩深度1.55 m 时位移、弯矩曲线

图5 嵌固深度2.6 m 时位移、弯矩曲线

1.3 土反力合力与负弯矩极值特征

嵌岩深度增加过程中的支护桩负弯矩极值、土反力合力迹线见图6。图6 具有明显的规律：嵌岩深度0.40～1.45 m，随嵌岩深度增加，土反力合力变小，负弯矩极值增大。越过了值域1.45～1.65 m，随嵌岩深度增加，土反力合力增大，负弯矩极值减小；嵌岩深度4.0 m 以下，土反力合力非线性增大，负弯矩在某一值附近波动。嵌岩值域1.45～1.65 m，土反力合力有最小值，弯矩极值有最大值，以此进行锁脚锚杆预应力等效替换。

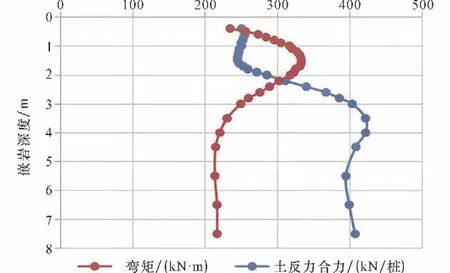
图6 负弯矩极值、土反力合力随嵌岩深度迹线

1.4 土反力分布特征与土反力合力的作用点

支护剖面上，取基底线X 轴（位移mm），向基坑内侧为正，取支护桩轴线为Y 轴（嵌岩深度m），向下为正。图4 工况，基底坐标为（3.53，0）；桩底坐标为（0.0，1.55）。位移曲线近似直线，所以任意一点的位移满足方程：

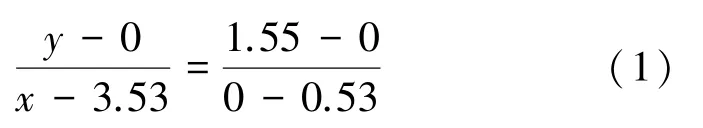
根据JGJ120-2012 规程，可以推导出：

分布土反力Ps=113.88y（3.53-2.277y）+2.022=-259.305（y-0.7751）2+157.824

单桩计算宽度的土反力合力Psk=Ps（y）dy=244.0

理正软件计算结果为245.1，相对误差不足1.0%，计算表明坑底位移曲线为直线的假定是合理的。分布反力随嵌固深度曲线见图7，土反力合力作用点位于嵌岩段中点处。

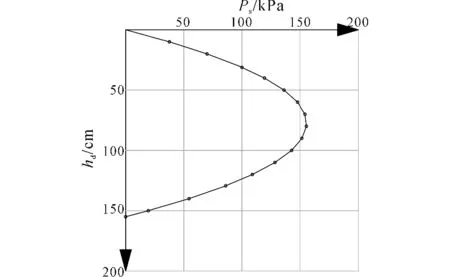
图7 分布土反力—嵌岩深度曲线

2 迹线法设计说明

迹线法的核心是求取土反力合力的大小，并确定作用点。基本过程如下。

寻迹：试算桩端铰接值域，选值域中值为嵌岩深度（hd），0.5hd为土反力合力作用点。

求作用力矩：取土反力合力Psk作为水平作用标准值，力臂取0.5 嵌固深度+顶层支点到基岩面的距离。

求等效支锚水平反力Fh：力臂取等效支点到顶层支锚的距离，令作用力矩等于等效支锚水平反力矩，求得Fh，进而按规程计算支锚极限抗拔承载力Rk。

3 工程实例

临沂中汇广场基坑进行支护设计时采用了这种方法，采用1.1 节参数，基坑开挖深度17.0 m 岩肩宽度小于0.8 m，土反力合力取244 kN，作用点在岩面以下0.775 m；锁脚锚索设在基岩面以上0.5 m处，换算为等效支锚水平反力为300.0 kN，锁脚支锚轴向极限抗拔承载力标准值计算结果为558.9 kN。锁脚锚索采用3 束φs15.2 mm 1860 级钢绞线，支护结构水平位移和竖向位移最大值小于10 mm，锚索设计值监测未达到报警值19.2 mm。

4 结论

计算结果与工程监测结果表明，采用迹线法对岩肩宽度不足时，来确定锁脚锚索支锚力和支锚点的设计方法可靠，采用软件计算土反力合力简便易行，经过3～5 次试算就可找到支点力大小和作用点。这种方法用于确定锁脚锚杆支点力大小是确定的，避免人工干预带来不确定性，有利于技术人员使用推广，对类似工程具有借鉴意义。