基于半空间模型和弥散试验的场地地下水污染物自动溯源算法研究

王蕾，张芳，王成锋，徐振飞

（四川省地质工程勘察院集团有限公司，四川 成都 610000）

0 引言

场地地下水污染具有隐蔽性、复杂性和突发性等特点，导致污染物的来源识别存在较大困难，快速识别污染源发生的位置对于场地修复治理、防控措施的制定具有重要的研究价值（张辰等，2018）。要展开地下水污染治理工作，首要步骤是根据有限的观测数据结合数据模型方法，找出污染源的位置及污染物的运移路径（杨海东等，2014）。目前地下水污染物溯源的方法，主要分为两大类：地球化学足迹法和数学模拟法（龙玉桥等，2017）。由于污染物的扩散和运移是一种随着时间演变的过程，故单独使用地球化学足迹法不能完全解决污染物的溯源问题。而数学模拟法的研究多集中于简单的理想算例（赵勇胜，2012），实际工程应用中，需要考虑研究场地的含水层参数、污染物类型等因素的影响（陈正侠等，2017），导致数学模型的建立对使用者的专业素质要求较高，这限制了它在普通研究人员和用户中的推广使用。

本文提供一种场地地下水污染物自动溯源算法，该算法利用地球化学足迹法和数学模型相结合的方式，通过弥散实验获取研究场地水文地质参数（沈婷婷，2015），将场地巡检操作和污染物排查经验量化为数学模型，该模型在研究场地的应用将推进类似场地地下水监测信息服务的智能化，提高地下水污染源分析研判的效率，缩短污染事故的应急处置时间，有效减少地下水污染带来的环境破坏，在一定程度上减少因事件而造成的经济损失和社会影响。

1 研究区概况

研究区地下水资源丰富，区内浅层地下水属孔隙潜水，受自然地质环境条件的限制，天然防护条件差，防污性能差，地下水环境脆弱。当生产装置发生渗漏时，如不及时监测、预警和采取相应处理措施，可能造成严重的地下水污染及快速向下径流，影响到厂区下游城镇及分散农户供水安全（姜凤成等，2017；陈书客等，2019）。厂区面积约4.6 km2，厂外排水管线长约77 km，厂内合计监测及应急抽水井168 口，厂外排水管线及沿线监测井25 口，共计193 口监测及应急抽水井。针对研究区的地下水监测，已建成地下水监测原始数据库和预警数据库，开发了地下水监测信息管理系统，但随着地下水监测工作的深入，厂区地下水污染防控已经由单纯的监测预警发展到污染物溯源、溶质运移等综合分析方面，如何实现地下水异常时的及时溯源是目前工作区关注的重点之一，也是目前地下水监测领域研究的难点之一。

本文针对研究区的水文地质条件，研究一套自动溯源模型并将其设计转化为计算机算法，该套算法根据地下水流场、各装置特征污染物、各监测井水质情况进行分析判断，初步实现污染源追溯功能。算法将适用于具有类似地下水污染风险、布设有大量监测孔的孔隙型场地地下水污染防控工作中。旨在减少由于外部因素对监测结果造成的延判、误判，为地下水防控提供更加合理、科学的决策依据（孙江虎等，2016；孙杰等，2019）。

2 模型方法

2.1 弥散试验应用

通过弥散试验得到污染物从试验主孔到各观测孔的最大和最小时间，从而利用时间位移公式计算出示踪剂到达观测孔的最小和最大速度。进一步的，利用观测到的水位数据和达西公式，计算监测孔对应的水力梯度和渗透系数。最后利用试验主孔和发现污染监测孔之间水力梯度、最大渗透系数，计算出污染物通过污染监测孔的可能最大速度，从而计算出污染物向下游可能运移到的最大位移（马佳等，2020；潘云鹤，2001）。

（1）采用多孔试验法开展弥散试验，试验主孔记为ZK1，主流向各观测孔记为ZGC1、ZGC2……ZGCn，侧向各观测孔记为CGC1、CGC2……CGCn。

（2）弥散试验中主流向观测孔ZGC1、ZGC2……ZGCn第一次捕捉到示踪剂的时间分别记为TZGC1、TZGC2、……TZGCn，各主流向观测孔至ZK1的距离分别记为LZGC1、LZGC2、……LZGCn，计算示踪剂到达观测孔的最大速度Vmax。

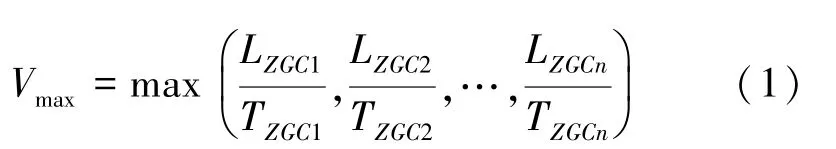
（3）弥散试验中侧向（无限接近垂直）观测孔CGC1、CGC2……CGCn第一次捕捉到示踪剂的时间分别记为TCGC1、TCGC2、……TCGCn，各侧向观测孔至ZK1 的距离分别记为LCGC1、LCGC2、……LCGCn，计算示踪剂到达观测孔的最小速度Vmin。

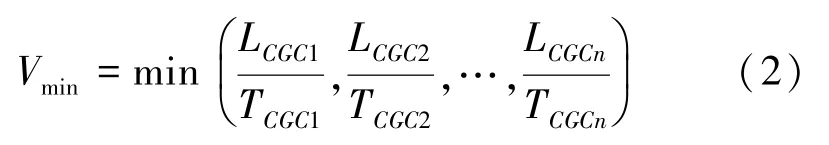
（4）记Vmax和Vmin的对应观测点为GCvmax、GCvmin，计算机程序利用观测点的水位数据通过等值线算法绘制穿过GCvmax、GCvmin的等水位线，得到GCvmax、GCvmin的水位值Hvmax、Hvmin，进而计算出GCvmax、GCvmin点位和试验主孔（ZKGC）之间对应的水力梯度Ivmax、Ivmin。

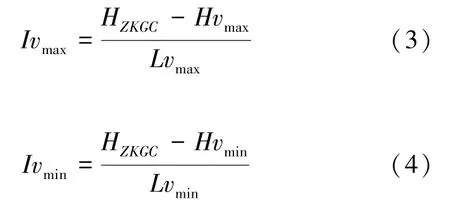
其中，L为试验主孔到观测孔的距离，HZ KGC为试验主孔的水位值。

（5）利用达西公式，计算含污染物的流体在GCvmax、GCvmin点位上的渗透系数K主、K侧。

（6）针对发现污染的监测点Ji（i=1、2、3...n），根据第（4）步绘制的等水位线，记Ji 的水位数据为HJi，进而计算出Ji水力梯度IJi。

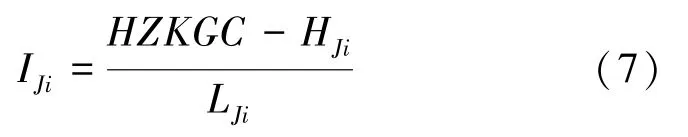
其中，LJ i为试验主孔到Ji的距离。

（7）利用达西公式，计算污染物通过Ji的可能最大速度VJimax。

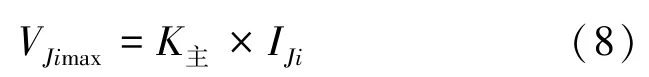
（8）计算场地装置发生泄漏时，在监测时间间隔T内，污染物沿地下水流向运移到监测点Ji的可能最大距离LJimax。

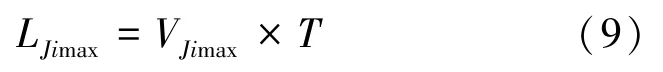
2.2 半空间模型

在一个空间内，半空间模型将所有样本分成两类，对于任意一个样本xi∈X（X是一个含有m个样本的样本集合，i=1，2，…，m）只会有两个状态，即f（xi）≥0 或f（xi）＜0（王玉琨等，2008；郑德涛等，1996）。在研究区的场地上进行地下水污染物的溯源模拟，溯源对象（装置）是否产生污染的状态数据正好满足半空间模型的样本条件（Willem F.Bronsvoort et al.，1993），即装置泄露和装置未泄露。为了将装置泄露的状态数据利用数学表达式将其中的连续变量表达出来（方德洲和李淼，2007），建立研究区适用的半空间模型，划分半空间Ai、Ai’，i=1、2、3…n，确定污染物溯源的有效搜索半空间是最终溯源的关键。具体实现方法如下：

（1）以发现污染监测点Ji为圆心，LJimax为半径画圆，该圆圈定的范围即污染源初始范围OA。

（2）以Ji监测点等水位线（水位值HJi）为分割法线，从空间上将污染源初始范围OA分割为两个半空间A1、A1’，A1内的所有监测点的水位值小于或等于HJi，即位于Ji下游；A1’内的所有监测点的水位值大于HJi，即位于Ji上游。

（3）标定两个半空间的属性，其中半空间A1置属性flag（A1）=1、半空间置A1’ 置属性flag（A1）=0。

（4）针对属性flag（A1）=1 的半空间A1内所有监测点进行搜索，如果存在污染点，则以水位值最小污染点作为圆心，重复上述（1）～（3）步骤的操作，直至区域Ai无其他污染点存在。此时，半空间Ai’即为有效搜索半空间。

2.3 锁定污染源

若有效搜索半空间Ai’内只有一个装置，则该装置为污染源泄露装置。若有多个装置，则在Ai’内搜索遍历所有装置，并利用半空间模型缩小污染源所在范围。具体步骤如下：

（1）利用现有场地的等水位线内插得到穿过装置中心点的等水位线，并将装置的水位记为HZ j，进而根据观测主孔和装置之间的水头差和距离计算出装置对应的水力梯度IZ j。

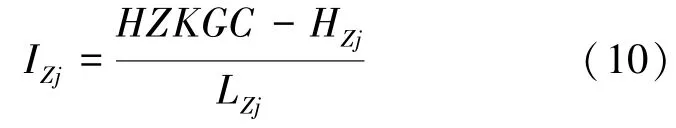
（2）利用达西公式和2.1 节中计算得出的K侧，得到通过装置Zj的可能最小流速VZjmin。

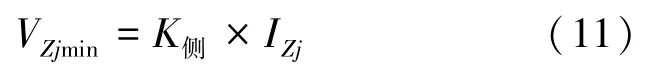
（3）计算监测间隔时间T内，污染物沿地下水流向运移到该点的可能最小距离LZjmin。

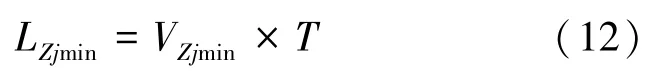
（4）以Zj为圆心，以该装置发生污染后污染物在T内的最小运移距离LZjmin为半径，绘制圆形OB。

（5）以穿过该装置的等水位线HZj为分割法线，从空间上将OB分割为两个空间Bj、Bj’，Bj内的所有监测点的水位值小于装置点水位值，即位于装置下游；Bj’内的所有监测点的水位值大于或等于装置点水位值，即位于装置上游。

（6）标定两个半空间的属性，其中半空间Bj置flag（B）=1；半空间Bj’置flag（B）=0，然后过滤掉flag（B）=0 无效半空间，保留有效半空间Bj。

（7）搜索Ai与Bj的交集区域内除了Ji以外的监测井，若存在无污染的监测井，则排除该装置是污染源的可能；若无监测井，或者有监测井且监测井全部污染，则装置Zj 有可能是污染源，记为Wk，k=1、2、3…m，m为可能发生渗漏的污染装置总数。

（8）Wk所在的范围就是污染源所在范围。

（9）将监测到的污染物类型与Wk内的特征污染物类型进行比对，具有同类型的污染物的装置即为泄露装置，即锁定污染源。

3 试验案例

3.1 试验数据

本课题选择的研究区早在2013 年就建立了地下水监测信息管理系统，系统包含自动化监测和人工监测两大部分，为研究区的地下水监测数据的传输、查询、分析、上报等工作提供了便捷的管理方式。但随着业务的持续开展，研究区地下水污染防控的需求已经由单纯的监测预警发展到污染物溯源、溶质运移等综合分析方面，而本课题的开展正是为了解决地下水中发现污染后污染物溯源的难题，课题组将第2 部分的模型方法编写为计算机算法，并形成单独的功能模块供系统调用，而基础数据（如监测井、装置等）则调用现有的系统数据库，课题的实验全部在该模块中展开。

表1 试验数据

试验实施前，课题组通过弥散试验已得到该场地示踪剂到达观测孔的最小和最大速度，并随机选择了两口污染监测井J1，J2，在系统操作界面录入污染监测井编号后，系统依照本算法流程开始了如下计算。

第一步：调取经过弥散试验得出示踪剂到达观测孔的最大、最小速度Vmax、Vmin，并自动定位对应观测孔，取出对应观测孔的水位进而计算孔的水力梯度Ivmax、Ivmin，利用达西公式，计算出含污染物的流体在GCvmax、GCvmin点位上的渗透系数K主、K侧。最后，针对本次发现的污染点J1，J2，计算其水力梯度IJ1、IJ2和污染物通过这两个监测孔的最大速度VJ1max、VJ2max。输入J1，J2的记录观测时间间隔T，计算出污染物可能运移到检测孔的最大距离LJ1max、LJ2max。试验数据如表1 所示。

第二步：弥散试验应用完成后，算法将继续执行，利用改进后的半空间模型确定本次试验的有效半空间，分别为A1′和A2′，由于J2在J1的下游，最终确定A2′为有效搜索半空间。

第三步：结合装置再次利用改进后的半空间模型进行污染源范围的缩小。在半空间A2’内搜索到装置Z1、Z2，发现Z1内对应污染监测井J1，Z2内对应无污染监测井J3。即可判断出Z1是疑似渗漏装置，Z2不是泄露装置（表2）。

表2 污染源锁定

3.2 效果分析

通过将上述模型算法应用于研究区现有的地下水监测系统中，经验证，该模型算法可行，起到了确定或缩小污染源范围的作用。图1 为算法验证流程图。图2 在监测系统上模型运行的结果，最终锁定一个装置为疑似污染对象，大大缩小了排查范围，提高了现场工作人员的工作效率。

4 结论

（1）本文选用的研究场地是项目组成员多年开展地下水监测、巡检和维护项目的实施地，是布设有大量监测孔的孔隙型场地。笔者对场地的地质、水文地质条件以及基本水文地质参数等资料均已获取，故利用弥散试验对污染物的最大、最小运移半径进行计算是较好的选择。

（2）将专家经验量化为数学模型，可以在一定程度上弥补当前数学模型理想算例脱离现实的情况，同时将其转化为地下水监测系统中的溯源算法并提供系统后台服务，用户通过填写巡检过程中的相关参数来运行服务，对用户的专业深入程度要求不高，可操作性较强。

（3）半空间模型结合场地装置的泄露状态数据，可以很好地发挥半空间模型的优势，同时也能提高算法的搜索的效率和准确率。

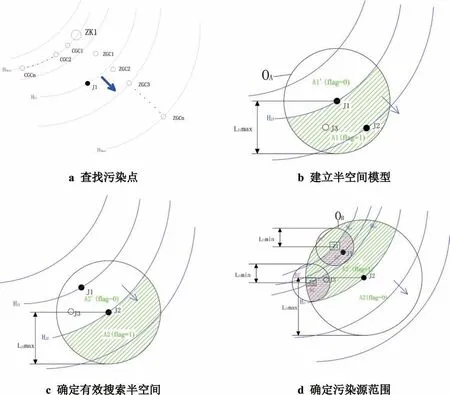
图1 算法验证流程图

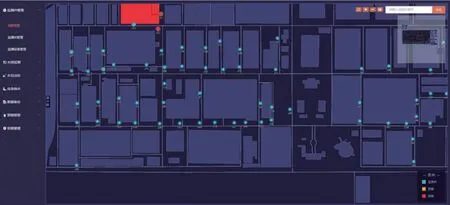
图2 污染物溯源效果

（4）溯源解析结果和现场实际经验研判基本吻合，因此，基于半空间模型和弥散试验的场地地下水污染物自动溯源算法是可行的。该算法的应用可为同类场地地下水污染事件的处理提供参考。