房地产业与金融业的波动溢出效应研究

付丽琴

本文采用MVGARCH-BEKK-t模型，以及Wald检验方式，对次贷危机前后的房地产业与金融业之间的波动溢出效应进行了研究。通过数据分析可以看出，我国房地产业与金融业自身的历史波动情况容易影响到相应的收益率波动，同时这种波动有着持久性和聚集性特点，但次贷危机前更加明显。

随着我国房地产业的快速发展，房产价格不断上涨，虽然我国制定了相应的抑制政策，但房价依然在持续增长，房地产业总体上呈现出一种非理性的发展景象。作为有着消费和投资双重属性的房地产，在发展过程中与金融市场之间的关系变得越来越密切。本文主要研究了次贷危机前后我国房地产业与金融业之间的波动溢出效应，同时对相应时期内，影响房地产业与金融业的相关因素进行了分析，以此来明确我国房地产业与金融业之间波动溢出效应的具体情况，以期能够为我国房地产业与金融业发展提供具有现实意义的参考依据。

一、BEKK模型及Wald检验

（一）BEKK模型

所采用的BEKK模型中，条件方差和协方差之间能够在互相影响的同时，还不用估计大量的参数，且能够有效保证最优化过程当中的条件方差—协方差矩阵相应的正定条件，这一模型在实际研究中有着较为广泛的应用。本文所采用的残差所服从的是t分布的二元BEKK（1，1）模型对房地产业与金融业波动溢出效应进行建模。

Rt=?+εt，εt|It-1～T（0，H，v）                             式1

Ht=CC'+Aεt-1ε't-1A'+BHt-1B'                                  式2

式1是向量形式中所表示的均值方程，其中Rt所表示的是2×1维的向量，分别表示的是房地产业和金融业的收益率;?所表示的均值向量（2×1维）;其中参数v是t分布的自由度。

式2所表示的是方差方程，其中Ht所表示的2×2维的对称矩阵，这一矩阵所表示的是当条件残差在t时刻时的方差—协方差矩阵;C是下三角矩阵;A表示的是ARCH项相应的系数矩阵;B表示的是GARCH项中的系数矩阵;其中的C'、A'、B'是与C、A、B对应的转置矩阵。其中Ht具体展开为：

式3

矩阵A当中的对角元素αii（i=1，2）所反映的是ARCH效应，矩阵B当中的对角元素βii=（i=1，2）所反映的是GARCH效应，也就是市场1与市场2当中的时变方差的特征以及波动的持久性特征。在矩阵A以及矩阵B相应的非对角元素所反映出来的市场1与市场2相应的波动溢出效应，其中元素αil（i≠j）所表示的是j波动率对于i相应的冲击程度，能够将波动溢出中的ARCH效应反映出来。对于元素βij（i≠j）所表示的是j对于i相应的波动率传导的持久性，能够将波动溢出的GARCH效应反映出来。如果市场1表示的是房地产业，市场2所表示的是金融业，那么其中h11，t就是t时刻房地产业的收益率序列条件方差，h22，t就是t时刻金融业的收益率序列條件方差。而h12，t-1=h21，t-1是t时刻房地产业与金融业条件协方差，其中的ε1，t-1和ε2，t-1则分别表示的是房地产业与金融业在滞后一期的残差项。

（二）波动溢出效应的Wald检验

根据式3可以看出，房地产业与金融业所产生的波动，主要是其自身与对方在前期波动的情况，以及相应的协方差h12，t-1、自身和对方在前期的残差平方、前期残差之间所形成的相互的影响ε1，t-1ε2，t-1。所以，对于房地产业与金融业来收，相互之间的影响不够显著时，自身波动情况主要有自身前期影响来决定。在Wald检验结果当中，其主要呈现非线性约束下的不稳定状态哦，同时在BEKK模型当中受到所设定形式的限制，因此，在本次研究当中，关于房地产业与金融业波动溢出效应，可以只针对相应的矩阵元素来进行相关检验。这样可以做出这样几种假设：（1）房地产业与金融业之间不存在波动溢出效应，也就是α12=β12=0、α21=β21=0;（2）房地产业对金融业不存在波动溢出效应，也就是α21=β21=0;（3）金融业对房地产业不存在波动溢出效应，也就是α12=β12=0。

二、房地产业与金融业波动溢出效应检验

（一）数据选择和描述性统计

关于房地产业与金融业波动溢出效应的检验中，所选择的数据为深圳地产指数与金融指数。所选择的样本区间为2001年7月2日～2014年4月28日，一共有3111个交易日数据。在本文中，所采用的是对数收益形式，其中日收益率的计算式为：Rt=ln（Pt/Pt-1），在这一式中Pt所表示的是房地产指数或者是金融指数在第t日的收盘价。

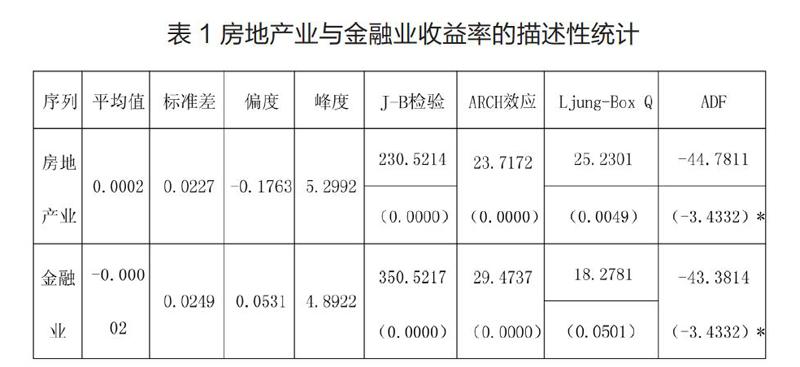
从表1中可以看出，所观察样本时间内，房地产业的平均收益为正，金融业收益为负，标准差相近。关于峰度统计量以及J-B检验统计量中，相关数据都显示两个序列并不服从于正态分布。从ARCH效应检验中就能够看出，两个序列之间有着较为显著的条件异方差性（之后10阶）。从Ljung-Box Q统计量中可以看出，相应的显著水平在5%以下，因此两个序列之间并不存在自相关性（滞后10阶）。在单位根ADF检验方面，序列明显平稳，只有1%的显著水平。房地产业收益率与金融业收益率都有着高峰后尾、条件异方差性，因此，都适合采用GARCH模型来进行建模。

采用双变量的MVGARCH-BEKK-t模型来进行建模，结合Wald方法来检验两者之间的波动溢出效应。在实证分析中，可以了解到房地产业与金融业的历史波动都会对当前的收益率波动产生影响，且这种波动影响，有着一定的持久性和聚集性。根据计算与分析，金融业对房地产业的波动溢出效应的影响不够显著，显著水平几乎为零，而房地产业对金融业的波动溢出效应有着1%的显著水平。在本次样本区间内，2008年发生的次贷危机对我国房地产业与金融业波动溢出之间的关系有着较为明显的冲击。次贷危机后，房地产业与金融业相应的波动效应的持久性与聚集性有所下降，其主要原因可能在于经济复苏的不确定性以及房地产业政策调控等影响，因此市场保持谨慎的投资态度，投资策略在这一时间内调整较为频繁。

（二）结果分析

在对本次样本数据进行研究之后，可以发现房地产业对金融业存在单向的波动溢出效应，同时，这种效应的产生是在次贷危机后，也就是在次贷危机之前，两者之间并不存在波动溢出效应，在次贷危机后才产生了房地产业与金融业之间的单向波动溢出效应。深入研究“次贷危机前两者间不存在波动溢出效应”的情况，其主要原因是，本次样本所选择的“地产指数”与“金融指数”来分别代表房地產业和金融业，而在2001年至2005年期间，相应的股市处于熊市，股市交易不活跃，虽然在2006年我国基本上已经完成了股权分置改革，在股市中恢复了新股的发行，但相应的“地产指数”与“金融指数”信息在股市上的传递效率还是较低，同时，在次贷危机之前，虽然我国房地产业发展较为迅速，但其中占比较大的是投资性以及自住购房，投机套利在其中占比较小，房地产业发展结构比较健康，因此房地产业与金融业之间的联系不够紧密。且国有商业银行通过改革去除了银行不良资产，降低了自身的发展奉献，因此房地产业与金融业之间并不存在显著的波动溢出效应。

但在次贷危机之后，由于我国股市遭受重创，因此政府与业界开始重视房地产业的风险，在相应贷款基础利率经过多次政策性调整后，以及相关房地产购买政策的陆续出台，对股市中的房地产股和金融股产生较为明显的影响，进而也就对“房地产指数”与“金融指数”产生影响。房地产作为资本重要的依赖性产业，其资金的来源主要是银行贷款或者是上市后的融资，还有基金、期货、保险以及信托等相关金融类产业，因此，在地产价格暴跌后，作为抵押物的房产价值下降，银行业就会直接遭受影响，比如美国次贷危机就是典型的案例。而我国由于政策调控对房地产业有着较大的影响，同时，民间资本也有着更强的实力，因此，在金融业风险爆发后，虽然房地产业从银行很难获得融资，但政府可以通过出台“取消限购”、“买房落户”等有利于房地产业的政策来进行“救市”，这样就使得房地产业很难被金融风险所影响，因此，虽然理论上金融业对房地产业可能存在波动溢出效应，但在本次样本研究中，结果显示金融业并不存在对房地产业的波动溢出效应。

三、结语

本文在研究房地产业与金融业的波动溢出效应中，采用MVGARCH-BEKK-t模型来进行建模。通过数据分析，我国房地产业受到政府政策性影响较大，且民间资本实力较强。次贷危机后房地产业对金融业存在单向波动溢出效应，金融业风险难以影响到房地产业的发展。因此，对于我国而言，应当进一步加强对房地产业风险的控制，防止风险向金融业扩散，才能有效保障我国社会经济的平稳运行与发展。

（作者单位：江西财经大学现代经济管理学院）

江西省高校人文社会科学研究2018年度项目：《我国房地产业波动溢出分析与动态投资组合研究（项目编号：GL18250）》。