基于多元回归分析的三体船阻力性能预报

许小颖，高丽莎

文华学院 机电学部，湖北 武汉 430074

近些年，三体船研究越来越受到人们的重视,特别是在其布局优化方面更是得到了许多学者的关注。郭春雨等[1]考虑到CFD 仿真模拟和模型试验之间存在不同之处,原有的自航试验数据处理方法其实并不适用于CFD 仿真模拟；陈康[2]等采用CFD 模拟技术对2 种不同三体船型的水动力性能进行了研究；而张校慈[3]基于实船、船模和浮动平台上设备的冲击响应测据,利用回归分析的方法汇总出一个实用的实验公式。这些研究普遍都取得了显著的成果，但上述研究方法一般是采用基于粘性理论的CFD 计算技术[4]，计算时间较长，不适用于大量的变换布局、航速的推广研究。

针对上述问题，笔者选取了基本数据库中29条包括货船、油船、集装箱船及化学品船的各相关数据进行了多元线性回归[5]，与计算机仿真模拟结果相对比，验证了回归公式的可行性，可将其广泛应用于三体船快速性能的初步预测中。

1 回归方法原理

回归分析是一种统计计算的方法，它从自变量和因变量的一组观测数据出发，寻找一个函数式(即回归方程)，将自变量与因变量之间的统计相关关系近似地表达出来。

在各种回归分析中，线性回归是比较常见的，而实际中的一些非线性问题通过变量代换也可转化为线性回归的问题，称为广义线性回归:

式中 ε表示误差，令

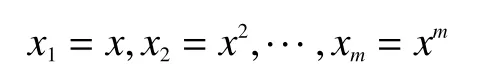
可将式(1)转化为

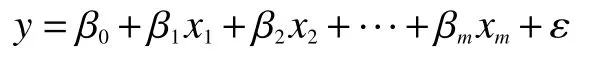
对于含有n个数据点的一组观测值(xi1,xi2，…，xim,yi),回归系数β0,β1,···,βm的确定通常可以用最小二乘法，使得残差平方和达到最小:

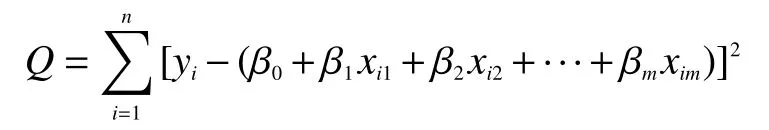
求得回归系数后，须进行检验回归模型的显著性，通常采用F检验法[6]。分别定义

式中RSST为总偏差平方和，其自由度fSST=n-1。

假设H0: β0=β1=···=βk=0，当H0成立时，检验统计量F为

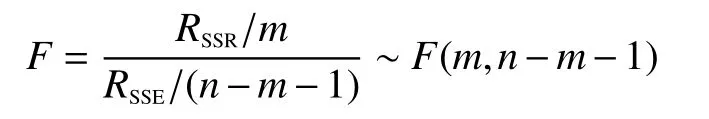
检验显著性概率为

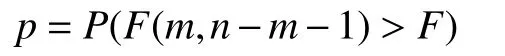
2 单体船阻力性能验证

2.1 样本数据库的提取

由于内河船在阻力因数上进行的模型试验[8]较少，采用基于武汉某研究所多条实船试验所得数据为样本，共有29 艘内河船，其中包括货船17 艘、集装箱船7 艘及油化船5 艘。数据库可在后续工作中进行补充。基于上述回归分析理论，笔者针对基本数据库中多条货船、油船、集装箱船及化学品船各相关数据进行统计以得到供本文回归计算使用的新数据库，该库以Fr=0.15～0.22为基本分类，表1 给出了各船的主尺度参数的分布范围。

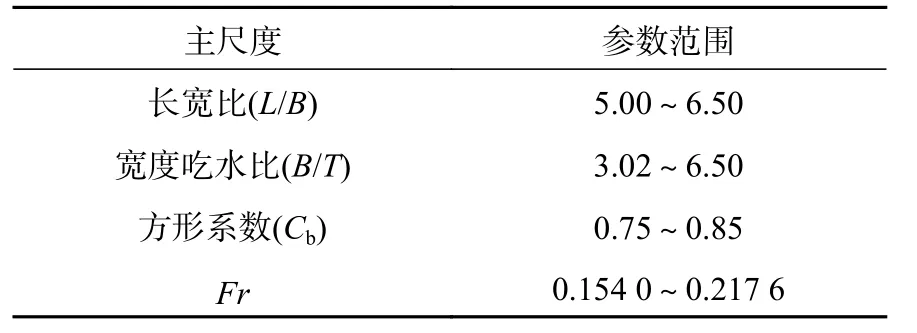
表1 基本数据库的船舶主尺度参数分布范围

由于每艘船主尺度参数的分布范围较广、基础数据较多，篇幅所限，表2 仅给出Fr=0.22 下的相关参数及其分布范围。

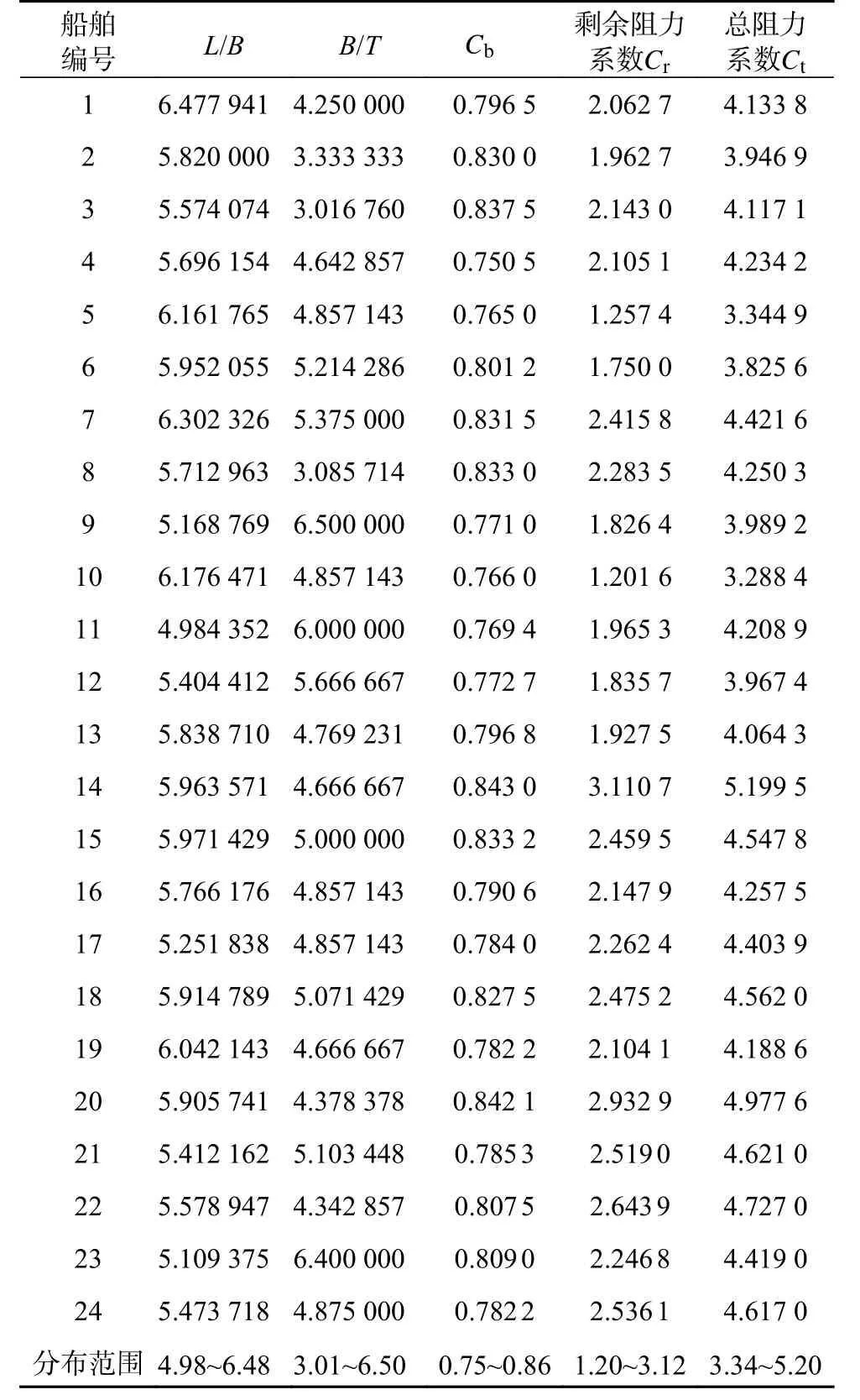
表2 Fr=0.22 时各船相关参数及分布范围

在显著性水平 α(一般取为0.05)下，当p＜α时，即认为回归方程有显著意义。另外，残差平方和越小，说明回归方程表达变量之间的统计相关关系的精确度越高，也就是回归分析的效果越好。

除了对回归方程的整体显著性进行检验外，还需对回归模型中的单个变量的显著性进行检验，以剔除对方程影响不显著的变量，得到最优的回归方程。通常采用的是逐步回归分析法，它的基本思路是:在给定的水平界限下，从一个只含常数项的回归方程出发，逐步引入和删除一些变量，对于每一步都进行显著性检验[7]。这个过程反复进行，直至既无不显著的变量从回归方程中剔除，又无显著变量可引入回归方程时为止。

2.2 样本回归分析

由于数据量较大，本文仅以Fr=0.15 为例，选定回归变量后，重复进行多元线性回归和检验[9]，期间剔除对方程影响不显著的变量和异常的数据点，由此得到剩余阻力的显著性检验结果:均方根误差RMSE=0.087 8，统计值F=10.907 1，其对应的概率p=0.000 1。可见p=0.000 1＜α，说明回归出的方程具有高度显著性。而回归均方根误差RMSE=表明了回归效果良好，该方程具有较高精确度。

最终得到的回归方程为

为便于观察，图1～3 分别给出了最终回归结果与原剩余阻力系数值关于L/B、B/T和Cb的对比图，可以看出回归值与原数据在分布趋势和数值上都吻合良好。

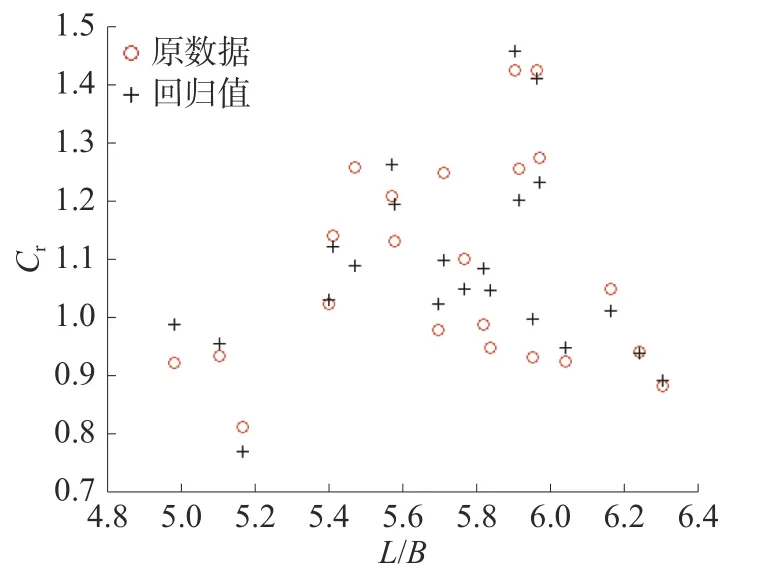
图1 回归结果与原始Cr 关于L/B 的对比

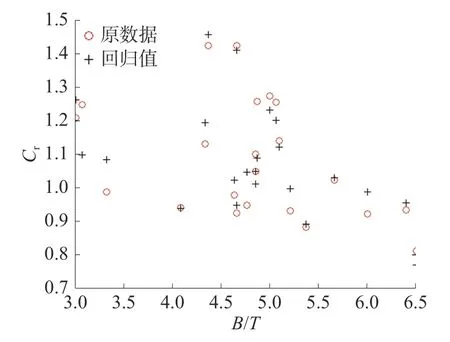
图2 回归结果与原始Cr 关于B/T 的对比

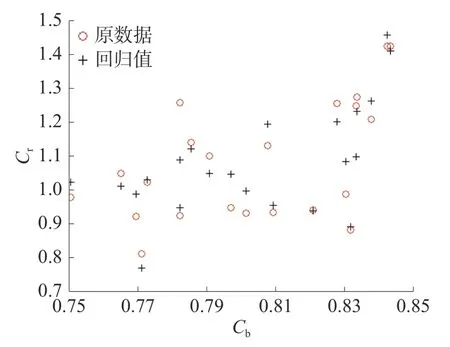
图3 回归结果与原始Cr 关于 Cb的 对比

通过国际船模实验会议(ITTC)1957 公式[10]计算实船的摩擦阻力系数:

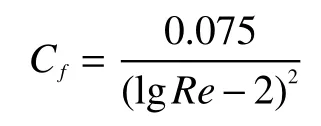
式中Re为雷诺数，可通过来求得，其中V可根据船舶主尺度及Fr求得， ν可通过查表获得。同时，需要计及实船粗糙度阻力系数

利用剩余阻力系数Cr的回归值，终可得实船总阻力系数:

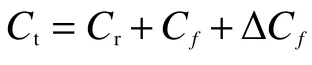
图4～6 分别给出了最终回归结果与原总阻力系数值关于L/B、B/T和Cb的对比图，可以看出回归值与原数据在分布趋势和数值上吻合良好。

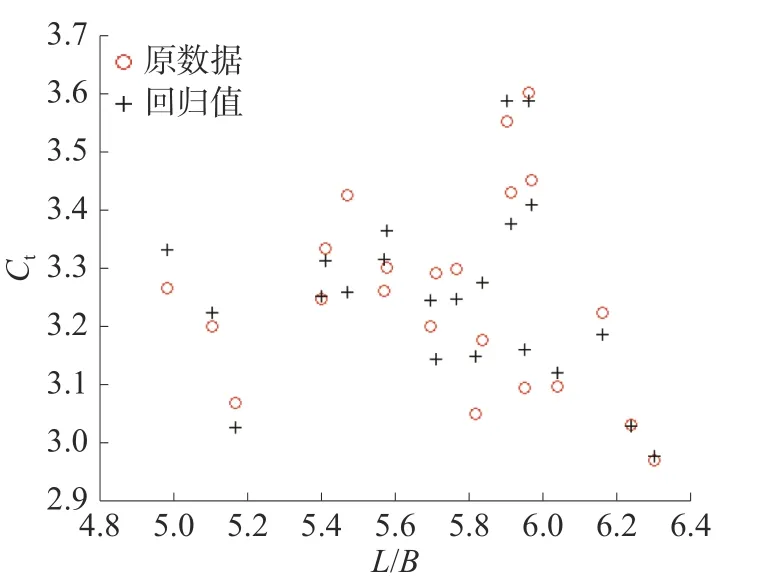
图4 回归结果与原始Ct 关于L/B 的对比

图5 回归结果与原始Ct 关于B/T 的对比

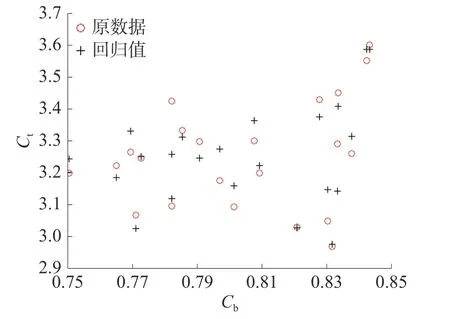
图6 回归结果与原始Ct 关于 Cb的 对比

为方便读取和验证，本文特摘取了Fr=0.15 时的回归数值，以列表形式体现表3 即为回归Cr计算实船Ct与原始试验数据的误差对比，由于不同Fr下样本数据的剔除点可能不同，故该表依据Fr不同其编号列有所不同。可以看出误差均为±5%以内，即回归公式具备一定可信度。

2.3 各不同Fr 下回归结果的统计

针对各不同Fr值，笔者依据上述过程进行了系数计算:

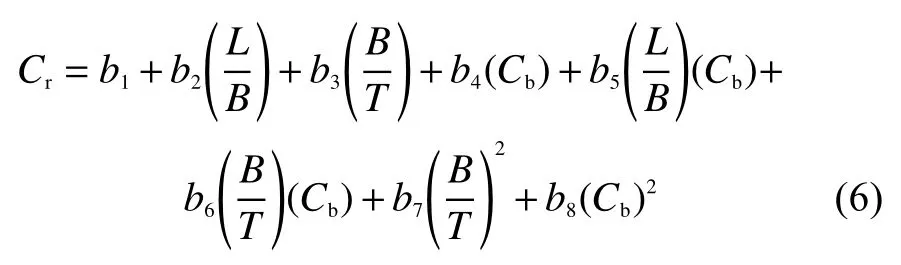
经过多次重复线性回归及异常点剔除后，在保证均方根误差RMSE、统计值F及其对应的概率p均满足一定要求的基础上，停止调试，并最终得到各Fr下的回归方程系数，见表4。将其分别代入式(5)即可得到不同Fr下的回归方程。

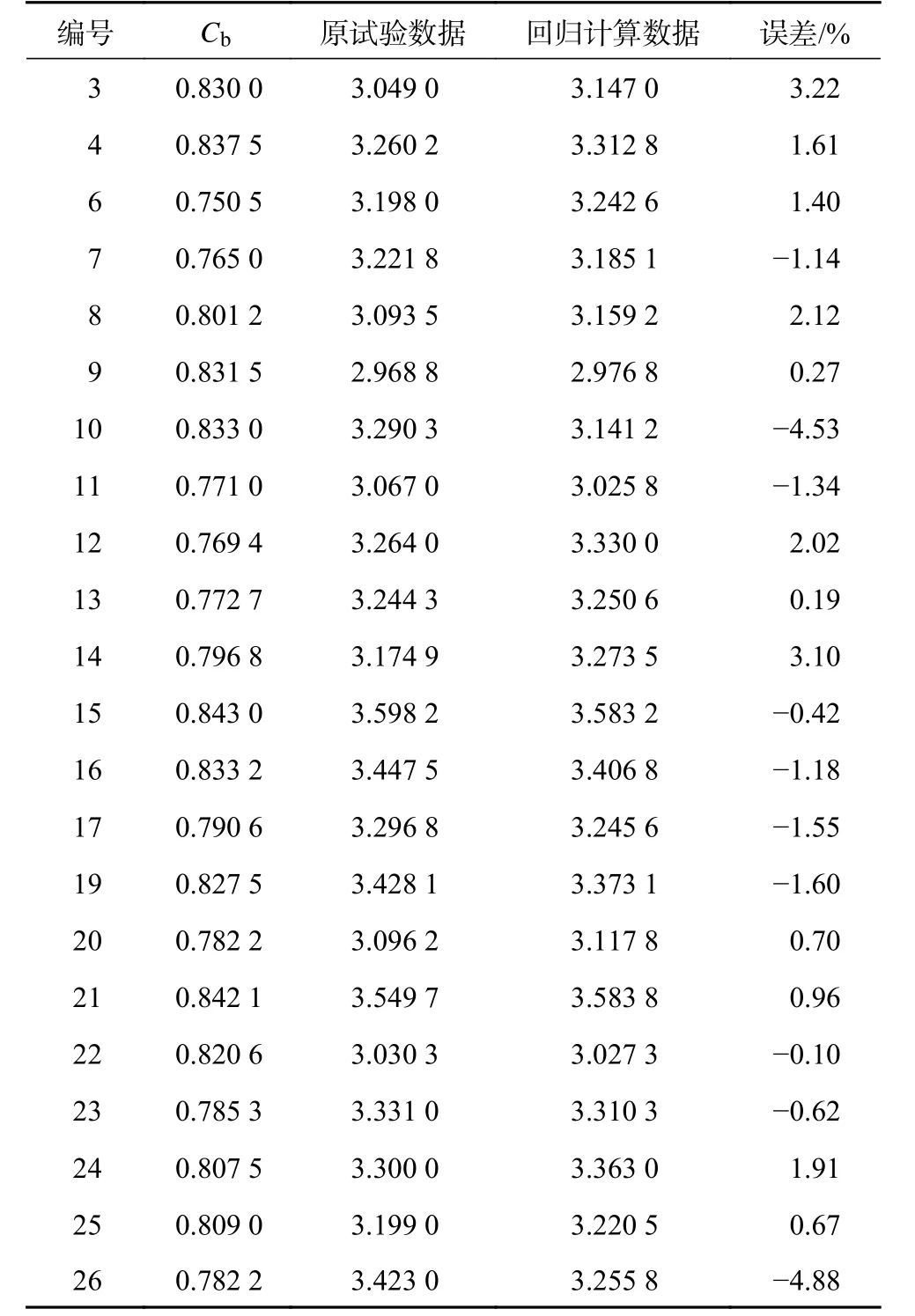
表3 Fr=0.15 时回归值计算得到Ct 值与原试验数据的误差

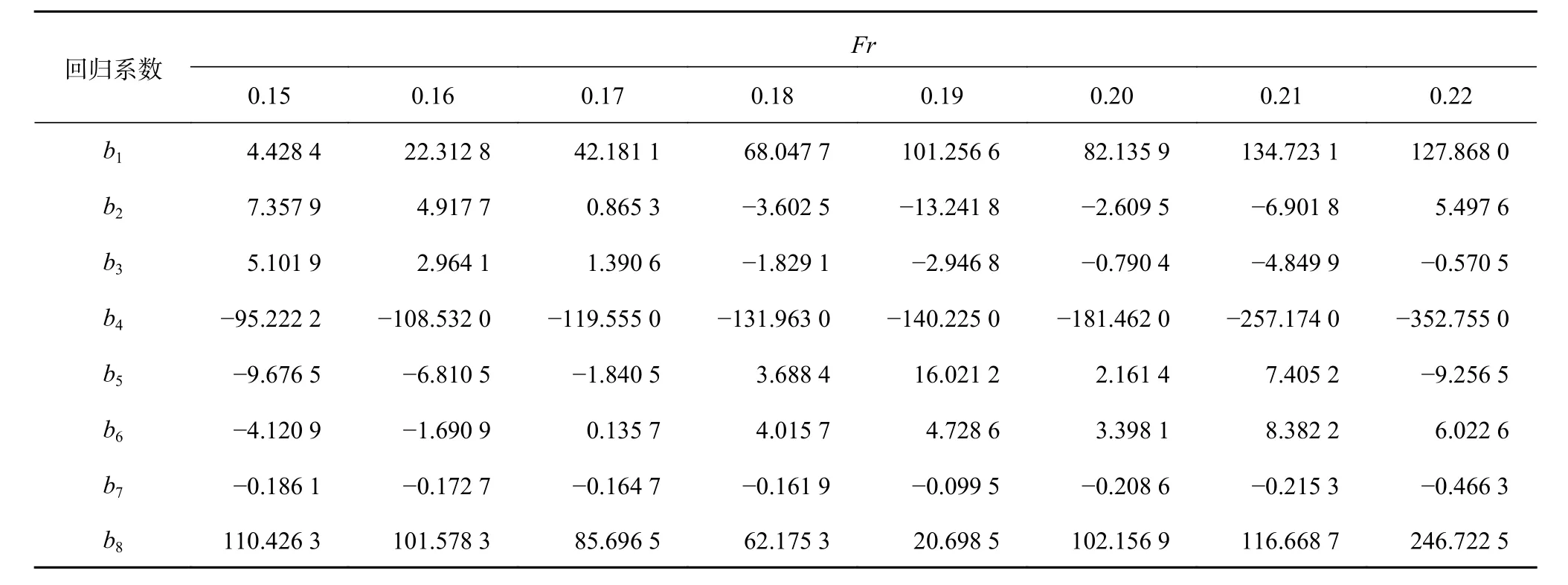
表4 Fr 不同时的回归方程系数

由表4 可见，公式中的常数项b1渐增，剩余阻力系数会随着Fr的增加而呈现增长的趋势；而只含有Cb项的系数(即b4和b8)绝对值较大，这说明Cb相较于其他主参数，对于剩余阻力的影响更大，且呈现规律性变化。

3 算例分析及预报

本文选用的是1980 年美国泰勒水池战舰5415(DTMB5415)的初步设计，带有艏部声呐罩以及方艉。该船主尺度参数见表5。

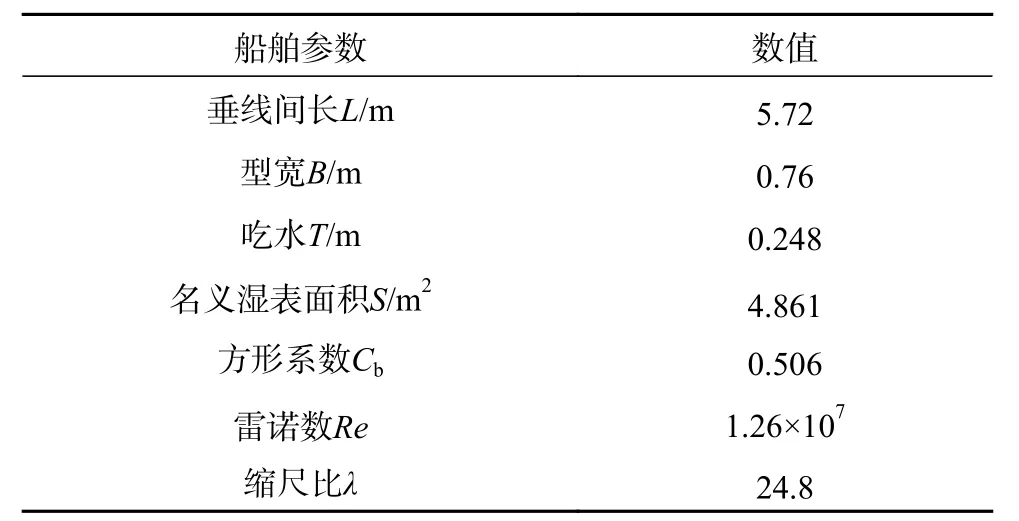
表5 单体船型主要参数

在前期笔者对于三体船布局优化的研究中，曾对该模型在各Fr下的阻力系数进行了仿真模拟[11-12]，如图7 所示。图中a表示主体与侧体的位置关系。

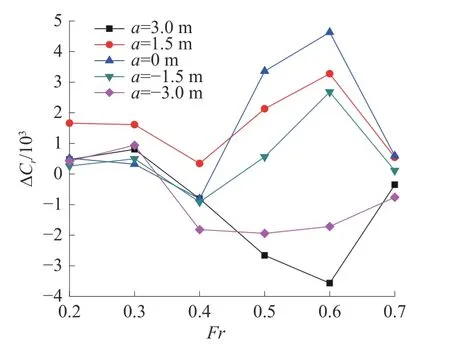
图7 不同布局下三体船的剩余阻力系数

取仿真模拟结果中的最优布局a=-1.5 m 即侧体后置前体1.5 m 的三体船的总阻力系数Ct，Fr取各种布局下阻力变化相差不大的数值(0.2～0.3)，将单体船的回归计算值转换为计算三体船总阻力系数值，通过对比CFD 仿真模拟结果与回归预测值，发现两值误差均在10%以内，详见表6。

表6 仿真结果与回归结果Ct 对比误差

分析误差原因主要有以下2 点:1)因理论分析的方法未能切实考虑到主侧体干扰对于三体船快速性能的影响，故结果存在一定误差；2)因样本数据的数量不多，且样本船型均有一定差别性，故回归公式中的误差数值具有一定局限性。

对于三体船的阻力预报，实验方法无疑准确，但成本较高；仿真模拟的方法也很常见，对于主侧体间的干扰也有涉及，但建模工作量较大且受网格质量影响较大；而回归计算方法用在初步设计阶段能够快速粗略地估算阻力数值，误差仅在10%以内，具备一定参考价值，可在一定程度上作为初期预测船舶阻力性能的有效手段。

4 结论

本文从快速性的角度出发，选取一定样本进行了多元线性回归，得到了单体船阻力系数的经验公式。后将换算得到的三体船阻力系数值与仿真模拟结果进行对比，验证了回归公式的可行性。在此过程中，与典型CFD 计算相比，多元回归的方法在精度接近的基础上，极大地节省了时间，而且无论是对样本的模拟，还是其大范围预测的能力都要远远强于CFD 模拟。

三体船的研究方兴未艾，多体干扰对于多元回归法预测三体船快速性的影响还需进一步研究，因此本文结果具有一定的局限性。同时，限于样本数据的多样性和局限性，多元回归公式具备一定变化性，由此出现的计算差别有待进一步讨论。