宽带成像目标模拟系统相位误差自提取方法研究
徐 啸,陆戈辉,黄 杉,王立权,柴娟芳
(上海机电工程研究所,上海 201109)
0 引 言
随着军事需求的不断增强以及射频频段的扩展,射频成像技术正在成为各个国家的研制热点。射频成像技术可在复杂战场环境下提高飞行器的精确探测和目标识别能力,已经逐步应用到战术飞行器上,如英国的“矛-EW”空对地导弹、“硫磺石”空对地导弹等。为开展射频成像制导系统的设计、验证与评估,对宽带射频成像导引头半实物仿真系统的设计研究已成为焦点[1]。
半实物仿真系统需要提供精确的成像目标回波模拟,用于成像处理算法、噪声和杂波抑制等研究。一般情况下,雷达利用电磁波探测目标,通过发射电磁波对目标进行照射并接收其回波,由此获得目标至电磁波发射点的距离、速度等信息。半实物仿真系统通过目标模拟系统对雷达发射耦合信号进行延时和多普勒调制,以此来模拟目标的回波,然而成像目标模拟系统对信号相参性要求很高,相位误差会引起图像的几何弯曲和分辨率下降,还可能导致图像信噪比下降和虚假目标的出现,严重时完全不能成像[2-3]。成像目标回波模拟系统一般存在多级上下变频,其中混频器、滤波器等模拟器件的非线性特性会造成传输信号相位畸变,进而降低系统的成像模拟精度[4]。因此,对于宽带成像目标回波模拟系统而言,信号严格相参是实现高分辨率成像模拟的前提,而如何准确地提取系统的相位误差是实现信号相参的关键。
对于目标回波模拟系统相位误差的提取,传统的方法是利用标准仪器搭建测试平台,如使用矢量网络分析仪测量通道的幅度相位信息[5]。这种方法依赖于仪器设备的指标精度,且每次测量都需要重新搭建平台,测试成本较高。本文提出一种利用宽带成像回波目标模拟系统自身的资源内建宽带幅相特征自提取方法,利用频率步进信号实现对大带宽范围的频率覆盖[6],同时运用全相位算法计算相位,抑制了由于截断操作产生的频谱泄露现象,提高了提取相位误差的精度。
1 回波相位误差对成像效果的影响分析
在宽带成像系统中,雷达接收机需要对多个回波脉冲进行相参积累,处理时间长,导致对目标回波信号相位很敏感,回波信号相位抖动会造成距离像的移动、波形发散[7-8]。本文以宽带成像系统中常用的频率步进信号为例来分析成像目标回波模拟系统的相位误差对成像效果的影响。频率步进信号是一种瞬时窄带、合成宽带的距离高分辨信号。它的信号形式为
(1)
式中:Tr表示脉冲周期时间;T表示脉冲宽度;N表示跳频个数;f0表示初始频率;Δf表示频率步进。
成像目标回波模拟系统的非线性特性对模拟的回波多普勒的影响较小,为简化设计模型,假设相对雷达距离R0处有一个静止的点目标,则回波信号的形式为
0 (2) 式中:τ=2R0/c,c为光速。 宽带成像目标回波模拟系统通过转发雷达主振信号,并调制相应的延迟来模拟目标位置。系统将雷达主振信号下变频到基带信号,调制处理完成之后再上变频到雷达发射频段,其间混频器、滤波器等多个模拟器件的非线性特性会将相位误差Δφ引入到回波模拟系统中,将Δφ代入式(2)中,则回波信号可表示为 e-j(2πf02R0/c+Δφi)e-j(2πiΔf2R0/c+Δφi)ej2π(f0+iΔf)(t-iTr), 0 (3) 式中,Δφi表示第i个脉冲内引入的相位误差;第一个指数项为常数项;第二个指数项包含距离信息。雷达接收并对模拟回波进行离散傅里叶逆变换(inverse discrete Fourier transform, IDFT)处理之后,可以计算出目标距离信息y(l′)为 y(l′)=y(l+lφ) (4) 可见,相位误差将直接影响模拟目标的距离信息,使得距离像偏移[9-10]。雷达接收机对存在相位误差的回波信号进行处理得到如图1(b)所示的距离像,主瓣出现开裂,旁瓣不对称等现象导致处理机对目标真实距离的提取错误,影响最终的制导精度[11-12]。 图1 相位误差对距离像的影响Fig.1 Influence of phase error on HRRP(high range resolution profile) 在宽带成像目标回波模拟系统中,当采样频率与信号频率不同步时,会造成周期采样信号的相位在起点与终点不连续,进而产生频谱泄漏现象,导致快速傅里叶变换(fast Fourier transform, FFT)之后的信号频率偏移,进而降低系统的相位测量精度,直接影响最终的模拟精度[8],如图2所示。因此需要选取一种能很好抑制频谱泄漏的数字信号处理算法,精确提取相位误差并加以补偿,以达到宽带成像目标高精度的模拟要求。 图2 频谱泄露引起的频率偏移以及相位突跳Fig.2 Offsets of frequency and phase due to spectral leak 全相位预处理是一种通过卷积窗对输入的成像回波模拟数据进行重排处理的方法,其目的是为了有效地解决由于数据截断带来的后续数字信号处理性能下降的问题。通过全相位数据预处理后的数字信号处理系统如数字滤波、频谱分析等系统,其首尾波形的连续性得到改善,谱线的泄漏效应也大大减小[8]。 设单频复指数信号为 x(n)=ej(ω0n+φ)=ej(n β 2π/N+φ0) (5) 式中:信号的数字频率ω0可表示为β倍的频率间隔2π/N(β可以是小数),则{x(n)}的FFT谱为 k=0,1,…,N-1 (6) 全相位算法的数据预处理过程如图3所示。对于某个待测样点,全相位算法通过穷举该样点的所有循环移位的情况,对于时间序列中的一点x(0),存在且只存在N个包含该点的N维向量。将每个向量进行循环移位,把x(0)移到首位,则可得到另外的N个N维向量。 图3 全相位数据预处理Fig.3 Processing of all-phase algorithm 对全相位数据预处理后的矩阵中的每行数都相加并取其平均值,则可得到全相位数据向量 x(N-1)+(N-1)x(-1)]T (7) (8) 对Xi′(k)进行求和平均即为全相位FFT的输出,即 (9) 提取式(6)~(9)中相位部分,即 (10) 由式(10)可以看出:全相位FFT各条谱线的相位值是一个确定的值φ0,该值即为中心样点x(0)的理论相位值,与频率偏离值(β-k)无关,也就是说全相位FFT具有“相位不变性”。这就为信号的相位精确提取提供了方法:首先对输入的(2N-1)个成像回波模拟数据做N阶全相位FFT,从得到的N条谱线中找出峰值谱线k,谱线k对应的相位即为相位值。 本文设计的基于全相位FFT的相位提取算法的现场可编程门阵列(field programmable gate array, FPGA)实现结构如图4所示。 图4 基于全相位FFT的相位提取算法实现结构Fig.4 Structure diagram of all-phase FFT processing 对于频率步进信号来说,每一个脉冲周期时间(pulse recurrent time, PRT)内的信号都可以看作是被截断的固定载频脉冲调制信号,利用全相位FFT,对其进行幅度和相位的提取;再将有效带宽内所有PRT所在频点幅值及其对应的相位合成,完成宽带成像仿真系统幅相特征自提取。 本文利用Matlab数字仿真平台对两种相位提取算法的提取精度进行评估。对频率为12 Hz,初始相位为100°的连续波信号,分别使用模拟器传统的FFT相位提取方法和基于全相位预处理的相位提取方法提取初始相位,其结果如图5所示。从图5(a)中可以看出,传统方法在频率点12 Hz附近的相位会出现突跳,最接近12 Hz的点为12.01 Hz,此处相位为57.06°,与初始相位相差42.94%;从图5(b)中可以看出,经过全相位变换之后,理想频点附近的相位恒定,均为100°,与初始相位一致。可见,全相位处理算法对截断原始时域信号的操作不敏感,进而能够准确地提取相位误差。 图5 两种方法提取连续波相位的对比Fig.5 Comparison of two algorithms about continuous wave 同样对载频为12 Hz、初始相位为100°的脉冲调制信号进行分析,分别使用模拟器传统的相位提取方法和全相位预处理FFT方法提取初始相位,其时域波形如图6(a)所示。从图6(b)中可以看出,传统方法在峰值频点12.01 Hz处的相位为66.27°,与设置初始相位相差33.73%;经过全相位变换之后,峰值频点处的相位为99.71°,与设置初始相位相差0.29%。经过多次重复实验,本文方法的相位提取误差均保持在0.4%以内,说明全相位预处理算法对连续波信号以及脉冲调制信号两种信号体制均不敏感,可以用于本文所设计的宽带成像目标回波模拟系统中,有效提取相位误差。 图6 两种方法提取脉冲调制信号相位的对比Fig.6 Comparison of two algorithms about pulse modulation signal 针对现有半实物系统中的宽带成像目标回波模拟系统的相位误差,分别利用两种算法进行相位误差提取,并使用相同的算法补偿由传统方法提取的相位误差以及全相位预处理算法提取的相位误差,补偿后的系统相频特性如图7所示,其中蓝色为模拟器传统的相位提取方法处理结果,红色为全相位处理结果。从图7中可以看出,经过全相位准确提取到相位误差之后,补偿效果显著,相位突变现象得到补偿,经过接收机处理得到的距离像也变得清晰,主瓣平滑,旁瓣对称。 图7 引入全相位提取算法后的成像效果验证Fig.7 Imaging effect of all-phase extraction algorithm 针对宽带射频成像半实物仿真系统中出现的相位失真问题,本文通过对全相位算法的分析,提出了一种基于全相位预处理算法的宽带成像系统相位误差自提取方法,并利用成像目标回波模拟器产生的步进频信号作为激励,内建全相位误差提取结构。仿真结果表明,这种内建的测量方法不仅简化了提取相位的复杂度,而且所提取相位误差小于0.4%,为后续半实物仿真系统中回波相位误差补偿提供保障。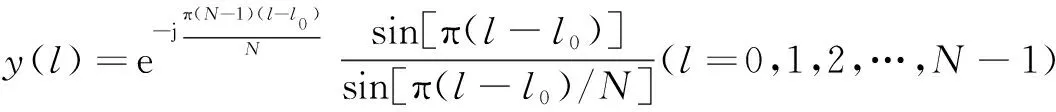

2 基于全相位算法的相位误差提取方法




3 仿真与实验验证
3.1 数字仿真误差对比


3.2 半实物仿真成像效果验证

4 结束语

