蜗壳形状对液力透平压力脉动影响的研究
赵万勇 ,马得东 ,史凤霞 ,梁允昇 ,彭虎廷 ,苗瑞林
(1.兰州理工大学 能源与动力工程学院,兰州 730050;2.甘肃省流体机械及系统重点实验室,兰州 730050)
0 引言
离心泵反转可作液力透平使用(PAT),可以通过做功的方式将钢铁、石油、化工等高耗能行业生产中产生的大量余压能量进行回收,压力能转换为液力透平的机械能,以轴功率的形式输出达到回收能量的目的[1-3]。由于液力透平的空间非对称性结构,其内部流动呈现出复杂的非定常特性,这将会引起流场的压力脉动,进而会对透平系统的稳定性造成不利的影响,因此研究透平蜗壳以及叶轮内部的压力脉动特性对提高系统运行稳定性具有实际意义[4-7]。
国内外有关液力透平压力脉动的研究主要是在不同流量下对液力透平各过流部件内的压力脉动进行了数值计算和试验研究[8-10]。除此之外还对叶轮与蜗壳之间的径向间隙、叶片数和分流叶片等对各过流部件内压力脉动的影响也进行了研究[11-12],但目前还鲜有关于不同形状蜗壳对液力透平性能影响的研究。薛珍宝等[13]通过试验研究发现,环形压水室内沿宽度方向的速度分布大都是不均匀的,特别是隔舌区域的速度变化较大,且任何工况下均存在回流。刘在伦等[14]通过对同一叶轮配两种蜗壳的高速部分流泵比较发现,采用矩形螺旋蜗壳能提高关死点扬程,且能提高泵的效率。而王洋等[15]发现,配环形压水室的微型离心泵综合水力性能较优于螺旋形的离心泵,且叶轮四周具有较为均匀的静压。因此,蜗壳形状对液力透平性能究竟有怎样的影响,有待讨论。
参考以上文献中蜗壳形状对泵性能影响的研究,本文对同一叶轮匹配两种蜗壳形状的离心泵作透平进行数值计算,研究蜗壳形状对压力脉动的影响规律,为提高液力透平的运转稳定性能提供了理论参考。
1 液力透平的主要几何参数
采用离心泵反转作液力透平,泵工况的设计参数为:流量Q=170 m3/h,扬程H=32.5 m,转速n=1 450 r/min,比转速ns=84.5,其主要几何参数见表1。环形蜗壳各个断面采用与螺旋形蜗壳第8断面相同的形状设计。
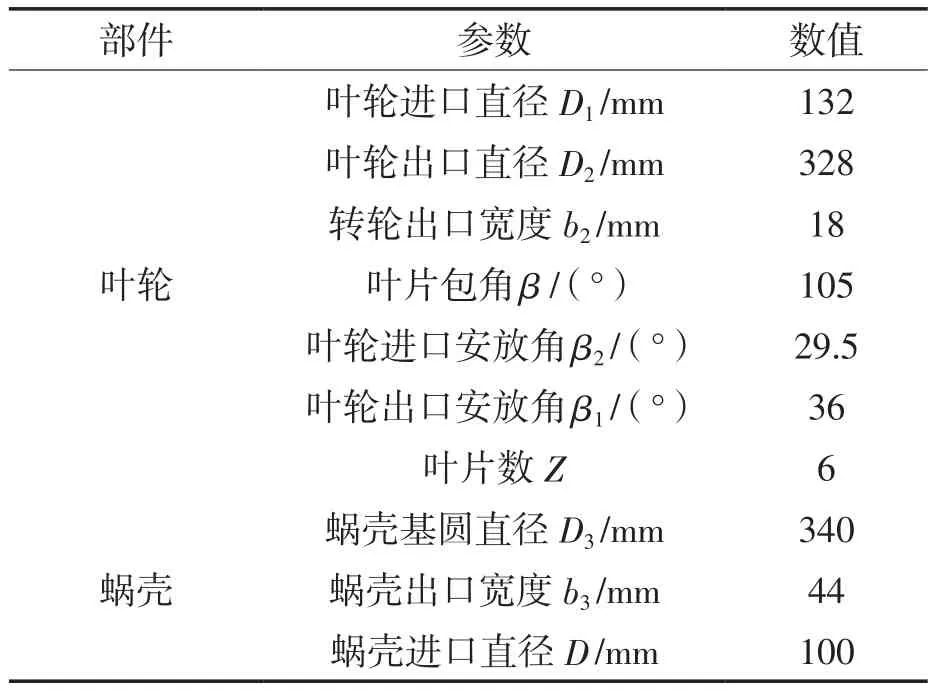
表1 泵作透平的主要几何参数
2 数值计算
2.1 计算域选取与网格划分
根据泵作透平的主要几何参数,利用Pro/e软件对液力透平进行三维建模,为了提高数值计算结果的准确性,对泵的进、出口段进行了适当地延伸,整个水体包括叶轮、蜗壳、间隙以及进、出口延伸段,得到计算流体区域如图1,2所示,环形蜗壳液力透平和螺旋形蜗壳液力透平的间隙以及进、出口延伸段相同。计算域生成之后采用ICEM对其进行混合网格划分,进、出口延伸段和间隙采用结构化六面体网格,而叶轮和蜗壳流道形状复杂,采用非结构四面体自适应贴体网格,并对蜗壳隔舌处的网格进行局部加密,如图3所示。对网格进行了无关性检查,如图4所示,当效率波动小于0.3%时可以认为网格对计算无影响,即满足网格无关性假设,最终确定的螺旋形蜗壳离心泵总网格数为140万、环形蜗壳离心泵总网格数为114万。
图1 螺旋形蜗壳液力透平

图2 环形蜗壳液力透平
图3 网格划分
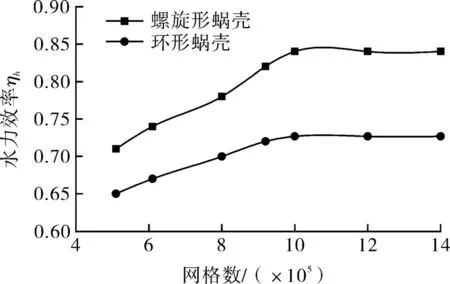
图4 网格无关性检验
2.2 监测点设置
为了研究液力透平内的压力脉动,在液力透平蜗壳和叶轮内部设置力一系列监测点,如图5所示。通过非定常数值计算实现监测点的监测,非定常计算时设一个时间步长叶轮转动4°,转速n=1 450 r/min,透平的旋转周期为T=4.137 9×10-2s,需要经过90个时间步叶轮转动一周,则一个时间步长Δt=4.597 7×10-4s。
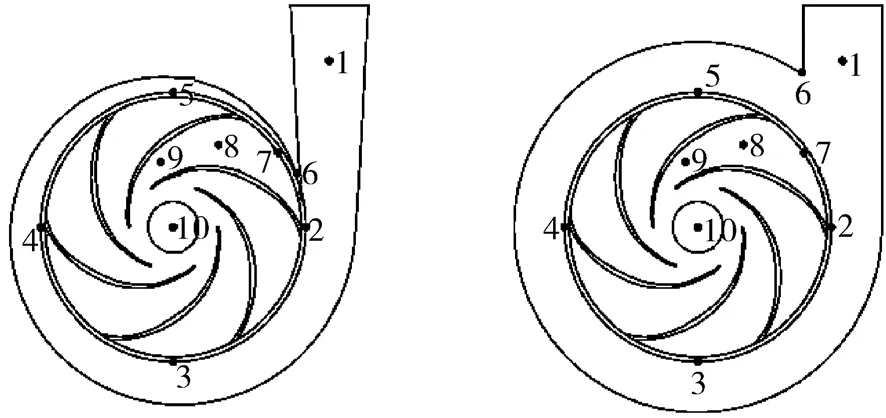
图5 监测点设置
2.3 湍流模型及边界条件设置
采用ANSYS CFX软件对模型进行定常和非定常数值计算。非定常计算是在定常计算的基础上进行的。非定常计算时叶轮总共旋转6周,选取最后一周的数值进行分析。采用雷诺时均不可压的Navier-Stokes(N-S)描述内部流动,选用标准k-ε湍流模型,动量方程和连续方程采用SIMPLEC算法联立求解,非定常计算时液力透平内部动静耦合面采用滑移网格技术,工作介质为常温下的清水。蜗壳进口采用速度进口,尾水管采用压力出口,一般设为0.4~0.6 MPa,本文设为0.4 MPa。固体壁面采用无滑移边界条件,近壁处采用标准壁面函数,收敛精度设为10-6。
3 结果分析
3.1 液力透平外特性分析
通过CFX数值计算,分别得到螺旋形蜗壳和环形蜗壳液力透平的外特性曲线,如图6所示。
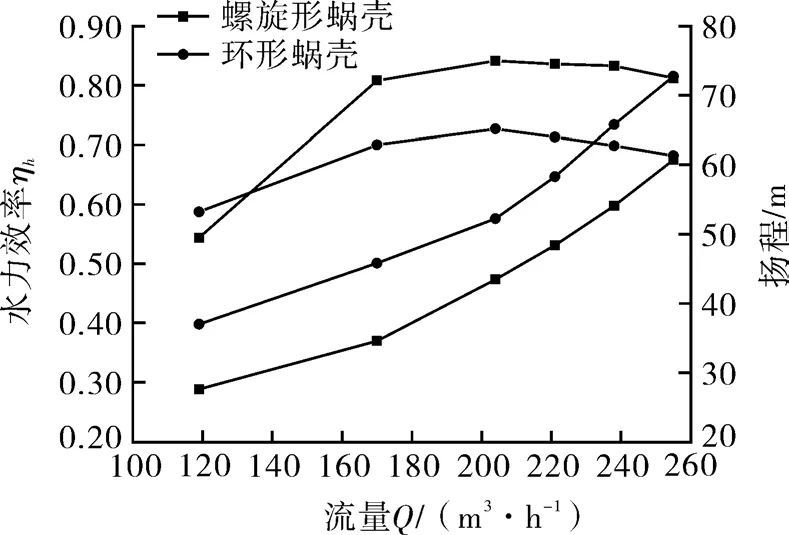
图6 不同蜗壳形状的外特性曲线
从图6可以看出,螺旋形蜗壳和环形蜗壳液力透平外特性变化规律相似,水力效率均随流量增加呈先增大到最大值再减小的趋势,水头均随流量增加呈缓慢上升趋势。在部分小流量工况(小于0.75Q),环形蜗壳液力透平水力效率高于螺旋形蜗壳液力透平,但之后随着流量增加螺旋形蜗壳液力透平效率均大于环形蜗壳液力透平效率,随着流量增加环形蜗壳液力透平水头均大于螺旋形蜗壳液力透平水头。螺旋形蜗壳与环形蜗壳液力透平的最优工况相同,均为1.2Q,然而最优工况下环形蜗壳液力透平效率要比螺旋形蜗壳液力透平效率低13.5%。究其原因,主要由于隔舌与叶轮间的间隙过大造成在各种工况下均有回流的产生,由于回流起到分流的作用[13],以至于环形蜗壳的水力损失比螺旋形蜗壳要大,所以环形蜗壳透平的效率比螺旋形蜗壳透平要小。
3.2 液力透平内流场分析
为了更加深刻地分析因蜗壳形状的变化而导致的液力透平性能的差异,对螺旋形蜗壳和环形蜗壳液力透平分别在1.0Q,1.2Q和1.5Q下的压力云图和速度云图进行了分析,结果分别如图7,8所示。
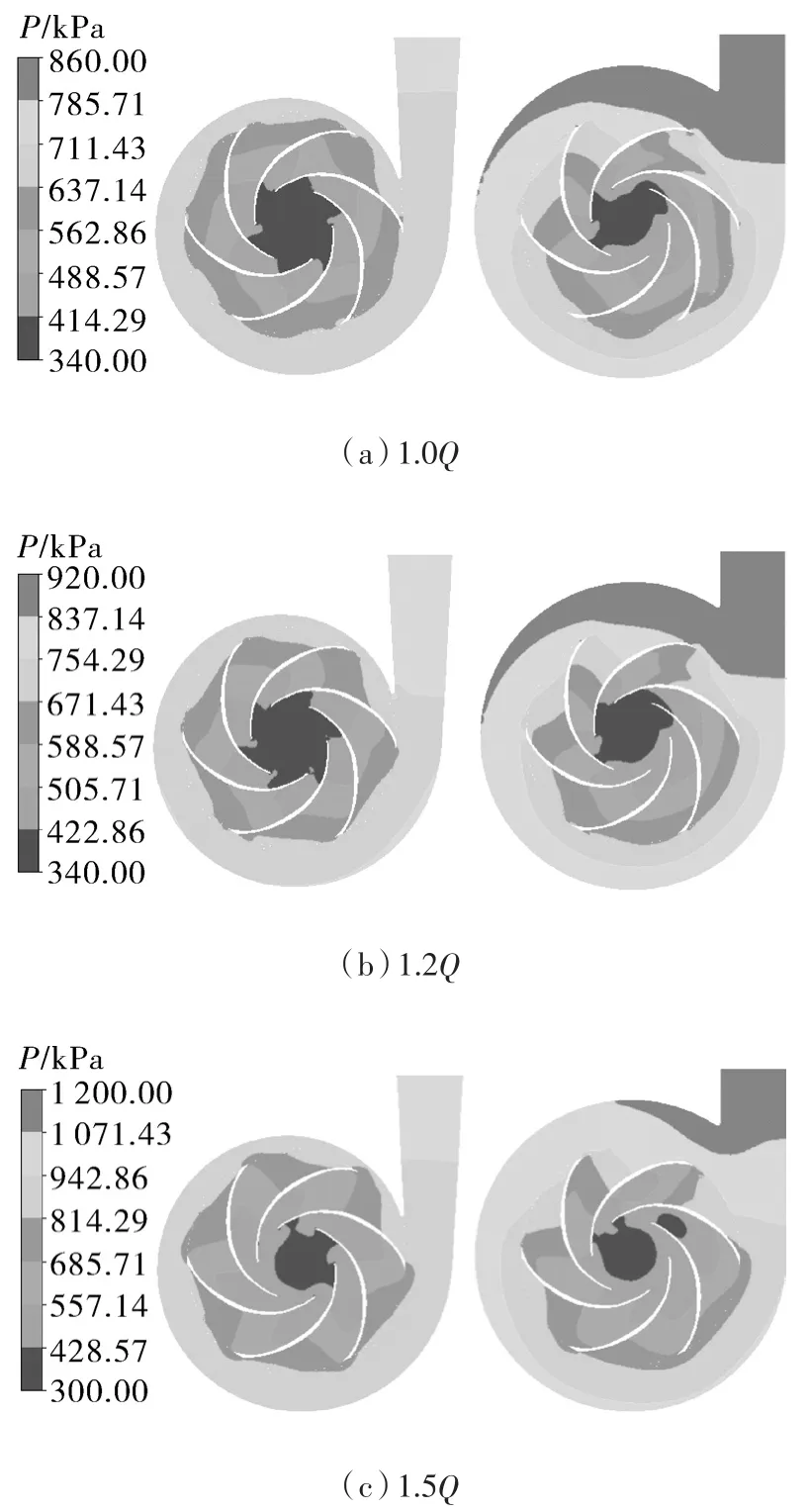
图7 压力云图

图8 液力透平速度云图
从图7可以看出,液力透平运行时,高压流体从蜗壳进口顺着蜗壳流道进入叶轮,最后从叶轮出水口流出,在流经叶轮的过程中,高压液体冲击叶轮对其做功使其旋转,液体压力沿着流道逐渐减小,压力能转换为液力透平旋转机械能,并以轴功率的形式输出来从而到达回收能量的目的[16-18]。同时由图7可以看出,2种透平模型压力分布梯度较明显,压力最低点都位于叶轮出口位置,这也符合液力透平压力能转换成机械能的做功原理。1.0Q,1.2Q和1.5Q工况下螺旋形蜗壳液力透平的进口静压力比其对应的环形蜗壳液力透平低,而出口压力力相同,这也符合外特性分析中螺旋形蜗壳透平效率大于环形蜗壳透平。螺旋形蜗壳透平叶轮的低压区面积大于环形的,但环形的没有螺旋形的低压区分布均匀。
从图8可以看出,螺旋形蜗壳液力透平从透平进口开始由于过流面积的减小,绝对速度从蜗壳进口到喉部逐渐增大,而环形蜗壳液力透平从透平进口到蜗壳喉部其绝对速度大小基本保持不变;所有透平叶轮内从进口到其出口绝对速度逐渐减小,低速区出现透平叶轮出口附近区域;环形蜗壳内沿宽度方向的速度分布大都是不均匀的,特别是隔舌附近区域的速度变化较大;螺旋形蜗壳内沿宽度方向的速度分布基本均匀;任何工况下,环形蜗壳内均存在回流,使环形体内的流速减小;环形蜗壳内流体的动能较大,但由于回流起到分流作用,从透平进口进入的液体动能将被有效的降低,这一结果和螺旋形蜗壳是不同的。
3.3 压力脉动分析
为了分析不同蜗壳形状液力透平内的压力脉动情况,对图5中透平内的一系列监测点进行了非定常监测,从计算结果中可以发现,蜗壳内各点的压力系数值不同,但各点的压力脉动规律基本相同,都呈周期性变化;叶轮内各点的压力脉动变化趋势相同,在叶轮流道中间处的压力脉动最剧烈。图9~11示出了1.2Q工况下一个周期内各个监测点在螺旋形蜗壳和环形蜗壳上的压力脉动时域。通过快速傅里叶变换(FFT)得到1.2Q工况下压力脉动频域,如图12~14所示。为方便下面的阐述,文中定义压力系数为Cp:
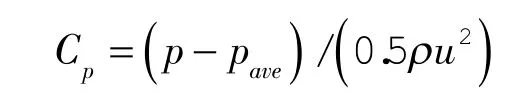
式中p——瞬时静压;
pave——平均压力;
ρ——介质密度;
u——叶轮出口圆周速度。
在图9~11中,横坐标表示透平叶轮旋转一周所用时间,纵坐标表示压力系数。图9中监测点1~6位于蜗壳上,一个转动周期内这6个监测点均呈现6个周期性变化,周期个数与叶轮叶片数相同;2种形式蜗壳最大压力脉动系数值均在监测点2处,主要是受动静干涉和隔舌的影响。通过比较可以看出:在螺旋形蜗壳上的各个监测点的压力系数均大于环形蜗壳上各监测点的压力系数,即螺旋形蜗壳上的各监测点的相对平均静压力均大于环形蜗壳上的;对监测点2,在0.22 s螺旋形蜗壳压力系数比环形蜗壳大30.7%。
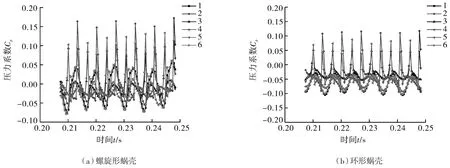
图9 监测点1~6压力脉动时域
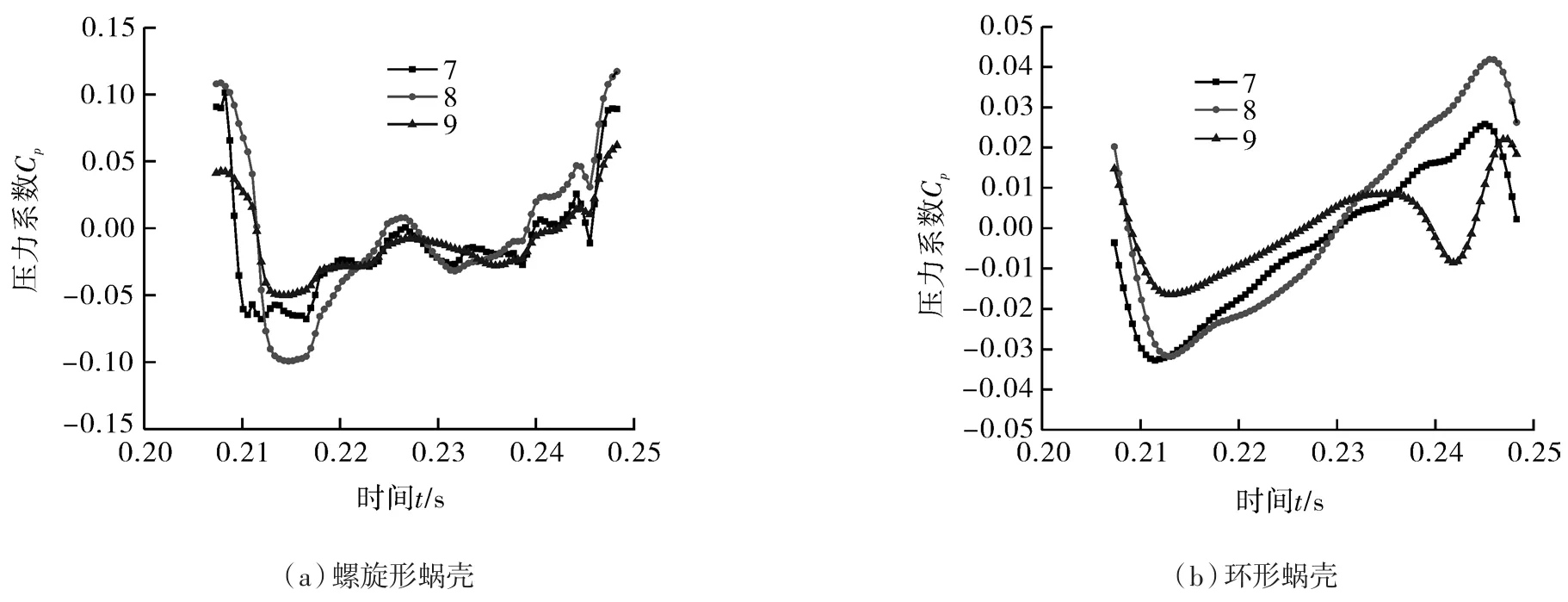
图10 监测点7~9压力脉动时域
图10,11中监测点7~10位于叶轮上,可以发现,螺旋形蜗壳的叶轮上监测点处的压力系数均大于环形蜗壳叶轮上监测点处的压力系数,且压力脉动更为剧烈。
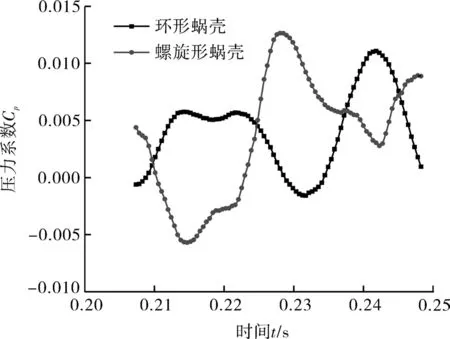
图11 监测点10压力脉动时域
在图12~14中,横坐标为频率,纵坐标为压力脉动幅值。叶轮转速为1 450 r/min,叶轮转频为24 Hz,叶频为145 Hz。从图12可以发现,蜗壳内部压力脉动的主频和次主频分别为145 Hz和290 Hz,因此液力透平蜗壳内部压力脉动的主频和次主频分别为叶频和2倍叶频;蜗壳上各个监测点的螺旋形蜗壳压力幅值要均比环形蜗壳大;在监测点6上,螺旋形蜗壳的压力幅值比环形蜗壳压力幅值高95%;在环形蜗壳上的监测点1和6,随着频率的增加其压力幅值趋向于平稳。从图13,14可以发现,叶轮内部压力脉动的主频为24 Hz,因此液力透平叶轮内部压力脉动的主频为叶轮转频;螺旋形蜗壳的叶轮各监测点上的压力幅值均大于环形蜗壳叶轮各监测点上的压力幅值;在监测点8上,螺旋形蜗壳的压力幅值比环形压力幅值高85%;环形蜗壳比螺旋形蜗壳在更小的频率处压力幅值趋向于平稳。
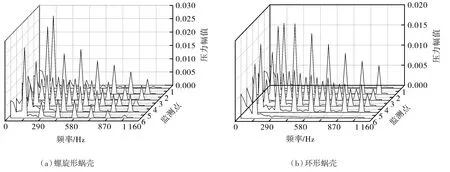
图12 监测点1~6压力脉动频域
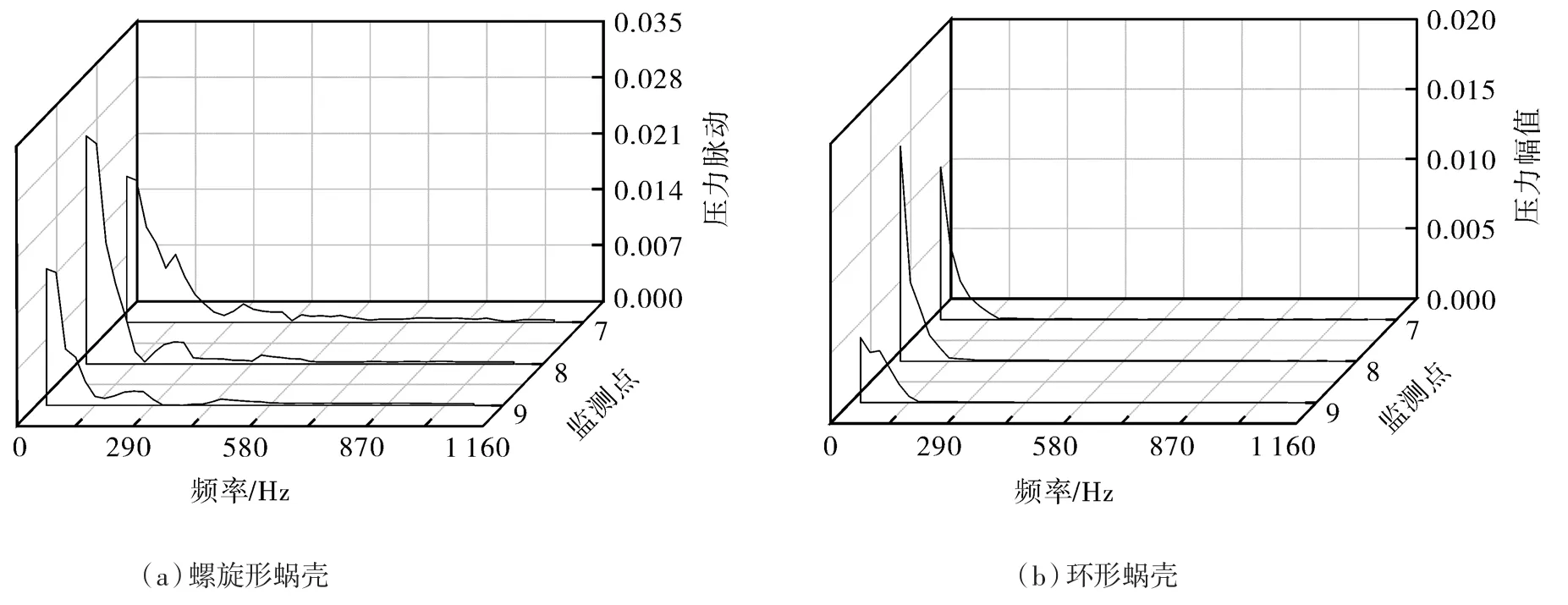
图13 监测点7~9压力脉动频域
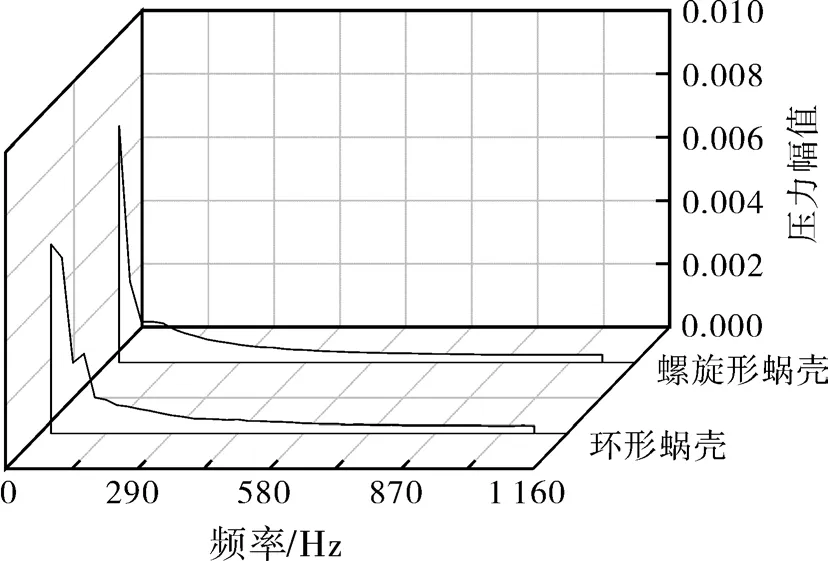
图14 监测点10压力脉动频域
4 结论
(1)最优流量和大流量工况下,螺旋形蜗壳液力透平效率均大于环形蜗壳液力透平效率;环形蜗壳液力透平水头均大于螺旋形蜗壳液力透平水头;螺旋形蜗壳内速度较环形蜗壳分布均匀。
(2)液力透平蜗壳内部压力脉动的主频和次主频分别为叶频和2倍叶频;蜗壳上各个监测点的螺旋形蜗壳压力幅值要比环形蜗壳大。透平叶轮内部压力脉动的主频等于叶轮转频;环形蜗壳比螺旋形蜗壳在更小的频率处压力幅值趋向于平稳。因此,从液力透平的回收效率和运转稳定性来看,虽然环形蜗壳的液力透平回收效率比螺旋形蜗壳透平的低,但采用环形蜗壳能大大提高透平的运转稳定性。

