基于历元星间双差模型的GNSS测速方法

靳少飞，杨震，顾和和，徐永明

(1.中国矿业大学 环境与测绘学院，江苏 徐州 221116；2.中国矿业大学 国土环境与灾害监测国家测绘地理信息局重点实验室，江苏 徐州 221116)

0 引 言

速度信息是描述物体运动状态的重要参数之一，在飞行器控制、船舶航行和车辆检测等领域具有重要价值。GNSS技术测量速度参数具有高精度、高效率、简单方便等特点。近年来，众多学者对GNSS测速方法进行了深入研究:何海波等[1]利用GPS数据分析了位置差分、多普勒和载波相位中心差分3种测速方法的精度及其与载体运动状态的关系,由于其算例中GPS观测值的采样频率为1 Hz，导致位置差分和载波相位中心差分的方法在载体速度变化较大时测速精度较低;吴富梅等[2]针对低成本GPS接收机只能观测到单频伪距的情况，提出了利用伪距差分测定载体速度的方法,该方法可以克服因载波相位周跳而产生较大测速误差的影响，但测速精度相对较差;李志斌等[3]利用北斗观测数据，分析了多普勒测速法和位置差分测速法各自的优缺点,当载体近似匀速运动时位置差分的精度较高，当载体运动速度变化较大时多普勒测速精度较高;王拓等[4]分析了卫星位置误差、卫星速度误差和接收机位置误差对多普勒测速精度的影响，同时比较了北斗3个频率不同多普勒观测值的测速精度，得出B3频率多普勒测速精度优于B1和B2频率的，当使用3个频率的北斗多普勒测速时，测速精度可优于0.1 m/s;张翼等[5]基于时间序列理论，对接收机钟差进行短期预测，并将钟差预测辅助载波相位时间差分算法进行解算，实现了恶劣环境下载体获取三维测速信息的功能。

由上述文献可知，利用GNSS进行测速主要有3种方式：一是利用定位结果(单点或RTK定位)，通过位置差分的方法获取速度；二是利用原始多普勒观测值计算相应的速度；三是利用载波相位差分计算速度。利用单点定位结果进行位置差分的方法获得的速度信息精度不高，容易出现较大粗差。利用RTK定位结果进行位置差分的测速方法虽然可以取得较高精度，但是需要2个GNSS接收机并且受限于基准站与流动站的距离，或者需要网络CORS端的虚拟参考站数据。利用多普勒观测值计算速度的精度主要受多普勒观测值精度的影响[6]。载波相位观测值由多普勒积分获得，所以利用载波相位差分测量速度和利用多普勒观测值计算速度的基本原理相同。多普勒观测值为某一时刻获得的反映接收机瞬时速度的测量值，载波相位差分是反映接收机在差分时间段内的平均测量值[7-10]。所以在接收机做近似匀速运动时，载波相位差分确定的速度比多普勒确定的速度更加平滑和稳定。

本文基于载波相位差分方法，提出了利用历元星间双差方法测量物体运动速度的模型，通过对载波相位进行历元和星间双差，计算历元间的相对距离，从而求取物体的运动速度。相对于载波相位差分法，本文方法通过观测值的星间做差可以进一步消除接收机钟差在历元间不一致的影响。当观测值存在周跳时，历元间单差不能消除观测值的整周模糊度，这会使测速结果产生较大误差。为了使该测速算法在观测质量较差、周跳频繁的环境中仍保持较高的可靠性，引入双差模糊度参数。进一步可将双差模糊度固定与否作为判断测速结果好坏的一个重要标志。若观测质量较好,不存在周跳，历元间单差可消除模糊度，双差模糊度可固定为0；若观测质量较差,周跳频繁，双差模糊度难以固定，虽然测速精度降低，但是本算法仍可保持一定的可靠性。

1 历元星间双差的测速模型

1.1 数学模型

历元星间双差模型通过对单个GNSS接收机的载波相位观测值先后进行历元和星间差分，将历元星间双差观测值当作观测量，以历元间接收机的位移量和历元星间双差模糊度当作待估参数进行求解。同一台GNSS接收机在k,k+1时刻的载波相位观测方程可表示为

(1)

式中：φ为载波相位观测值；ρ为接收机到卫星间的几何距离；N为整周模糊度；λ为载波相位观测值的波长；f为载波相位观测值的频率；上标p为观测的卫星；下标k，k+1为相应的观测历元；δtR和δtp分别为接收机和卫星端的钟差；I和T分别为电离层和对流层误差。

将式(1)做差，可得历元间单差观测方程，即

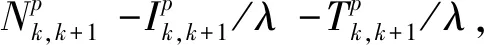
(2)

然后，将上述历元间单差观测方程在卫星p，q间求差，可得历元星间双差观测方程，即

(3)

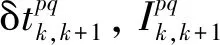
(4)

以历元间位移量和双差模糊度为待估参数，将式(4)线性化展开，可得

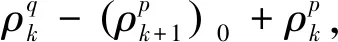
(5)

式中：l，m，n分别为测站到卫星的方向矢量在X，Y，Z坐标轴的方向余弦；dX，dY，dZ分别为测站坐标的改正量。

根据式(5)可以得到接收机在k，k+1时间段内的位移量，然后将位移量除以时间，便可以获得测站速度。

1.2 模型误差分析

1.2.1 卫星钟差

由于导航信号的传播速C很大，因此必须考虑钟差对测速的影响。卫星钟在时刻t的钟差一般可以表示为[11]

(6)

式中：a0为t0时刻该钟的钟差；a1为t0时刻该钟的速度(频偏)；a2为t0时刻该钟的加速度的一半(也称钟的老化率或频漂项)。

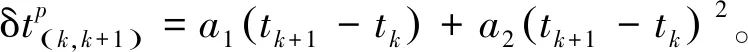
1.2.2 电离层和对流层误差

GNSS导航信号在穿过电离层时，传播速度会发生变化，变化程度主要取决于电离层中电子密度和信号频率。对电子密度沿导航信号传播路径进行积分就是总电子含量(total electron content，TEC)。当导航信号的频率确定后，电离层延迟的长短取决于TEC的大小。由于在短时间内TEC变化较小，因此，通过历元做差后可以显著消除这部分影响[13]。与电离层对导航信号的影响相似，当导航信号穿过对流层时，其传播速度也会发生变化，这主要与大气折射指数N有关。大气折射指数可分为干气部分Nd和湿气部分Nw。其中干气部分与总的大气压P及气温T有关，湿气部分则与水汽压e及气温T有关。因此，大气折射指数N在短时间内变化较小，通过历元做差后可以显著减小[14]。因为电离层和对流层在短时间内的变化比较缓慢，历元间的电离层和对流层误差相关性显著。因此，通过历元间差分后残留的电离层和对流层误差很小。

1.2.3 轨道误差

在GNSS相对定位模型中，卫星星历对相对定位结果的影响一般可用如下公式进行估计[11]

(7)

式中：Δb为卫星星历引起的基线误差；b为卫星基线长度；SS′为卫星星历误差；ρ为卫星到接收机的距离；(1/4)～(1/10)具体取决于基线长度、观测的卫星个数及其几何分布。

由于历元星间双差模型轨道误差的影响分析与相对定位的误差分析一样，因此可以利用此误差模型估算轨道误差对测速的影响。当广播星历的精度为2 m左右时，轨道误差对基线的影响一般<10-7m，对测速的影响一般<10-6m/s，因此，可以忽略卫星轨道误差对测速的影响[15]。

2 静态试验

在静态时速度真值为0，因此，通过静态试验可以分析历元星间双差、RTK位置差分和多普勒测速算法在理想环境下的测速精度。静态试验采用两台华测i70 GNSS接收机(RTK平面精度为±(8+1×10-6×D)mm，高程精度为±(15+1×10-6×D)mm)，在空旷环境中进行静态数据测量。试验数据采用GPS和BDS双系统观测值，静态观测时长为20 min，采样频率为5 Hz，高度截止角设置为15°。在静态试验中，接收机处于静止状态，然后将历元星间双差、RTK位置差分和多普勒测速方法所得结果与速度的真值0进行比较，从而测定观测噪声大小。通过与真值0比较可以获得3种测速方法的测速误差图，结果如图1～3所示(其中横轴表示历元,0.2 s，纵轴表示速度,m/s)，对3种测速方法的误差进行统计,得到对应方法的均方根误差RMS,如表1所示。

图1 历元星间双差测速误差Fig.1 Velocity error of double difference between epoch and satellite

图2 RTK位置差分测速误差Fig.2 Velocity error of position difference by RTK

图3 多普勒测速误差Fig.3 Velocity error of Doppler method

表1 3种测速方法的精度统计Tab.1 Accuracy statistical table of three speed measuring methods mm/s

由上述计算结果图1～3及表1可知：

(1)图1～3所示的3种测速误差在静态并且观测环境良好的条件下误差都比较小，且3种测速方法都没有出现粗差点。通过20 min的观测数据可知，观测噪声在一定范围内随机波动，并没有出现明显的系统性偏差。

(2)在静态且空旷环境下历元星间双差的测速方法效果最好，RTK位置差分的测速方法略差于历元星间差分的测速方法，多普勒测速方法最差,并且3种方法在E，N方向的精度都明显高于U方向。3种方法的U方向测速精度都比较差，这是由于GNSS在垂直方向上的观测值分量误差较大引起的。

(3)历元星间双差和多普勒测速方法的平均值虽然较小，但是明显大于RTK位置差分的平均值。这说明历元星间双差和多普勒测速方法存在着较小的系统性偏差。其中历元星间双差的方法，由于存在残留电离层和对流层误差，导致其在一定时间内平均值不为0。而多普勒测速值与接收机内部的载波跟踪环路有关，在一定时间内可能存在着较小的偏差。由于RTK位置差分的方法在历元间相关性弱，所以对一定时间长度的观测值求平均，该值接近于0，不存在明显的偏差。

3 动态试验

GNSS数据的观测质量在静态和动态环境下存在差别，为比较不同算法在动态环境下测速精度，本文进行如下动态试验。动态试验采用两台华测i70 GNSS接收机(RTK平面精度为±(8+1×10-6×D)mm，高程精度为±(15+1×10-6×D)mm)。一台架设在中国矿业大学环境与测绘学院楼顶，另一台架设在行驶的车辆上，试验路线如图4所示。该试验路线存在树木遮挡、高楼遮挡、山坡遮挡路段以及较为开阔路段，全长约7.5 km。试验数据采用GPS和BDS双系统观测值，动态观测时长为20 min，采样频率为5 Hz，高度截止角设置为15°。对采集的数据分别利用历元星间双差、RTK位置差分和多普勒的方法计算速度。

图4 动态测量试验路线Fig 4 Route of dynamic measureing

3.1 3种测速方法动态测量结果

为了对历元星间双差、RTK位置差分和多普勒3种测速方法进行比较，分别计算每种方法在E，N，U方向上的速度，结果如图5～7所示(其中横轴为历元,0.2 s，纵轴为速度,m/s)。

图5 车辆E方向速度Fig 5 The vehicle speed in east dirction

图6 车辆N方向速度Fig 6 The vehicle speed in north dirction

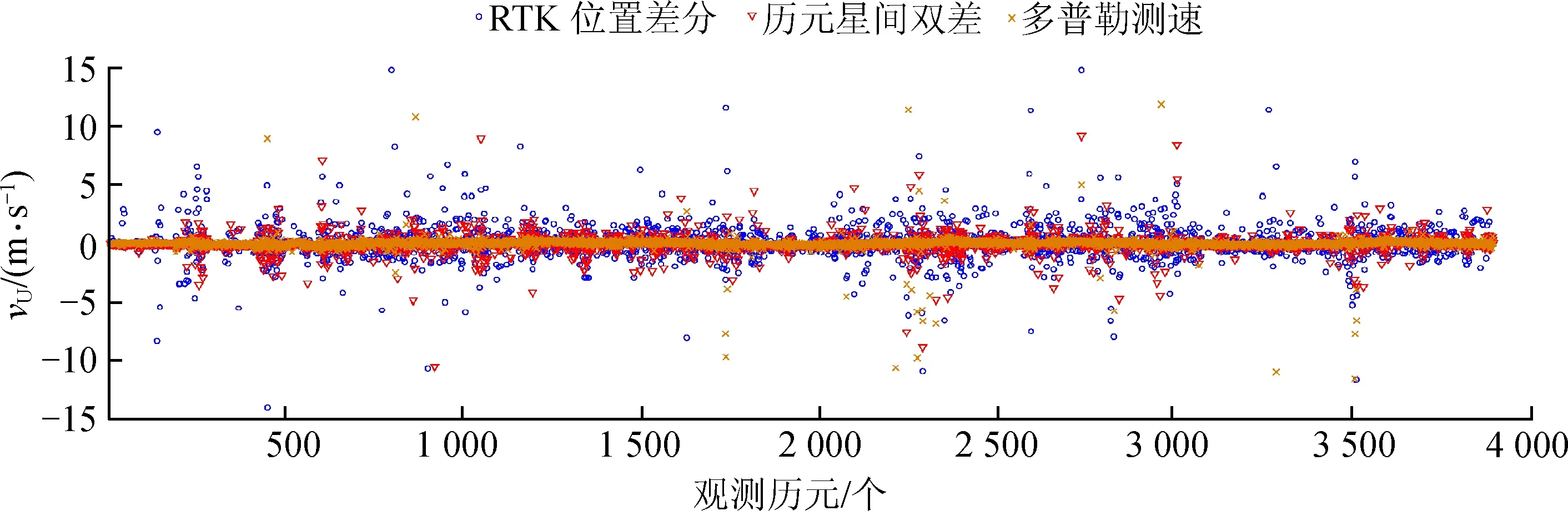
图7 车辆U方向速度Fig.7 The vehicle speed in up dirction

由图5～6可知，3种测速方法在水平方向的测速结果吻合。能够准确实时地反映车辆的速度变化。在观测条件较好的路段，3种方法都可以得到平滑、准确、连续的速度测量值。在观测条件比较差的路段，历元星间双差和RTK位置差分的方法都会出现较多的观测噪声，甚至是观测粗差。相较于历元星间双差和RTK位置差分的方法，多普勒测速方法抗干扰能力更强，在部分遮挡环境中仍然可以获得较好的测速结果。

图7中，由车辆在U方向的速度可知，观测环境变差时，历元星间双差和RTK位置差分的方法在U方向测速误差明显增大，会出现较多的粗差点。这是由于GNSS在垂直方向上的误差较大，使两种方法的测速结果都明显变差。

3.2 动态测量精度的评估

由图5～7可知，在动态且存在部分遮挡的环境中多普勒的测速方法明显优于其他两种测速方法，因此，将多普勒测速值当作参考真值分析其他两种方法的测速精度，统计结果如表2所示。为了评价历元星间双差和RTK位置差分测速方法的抗环境干扰的能力，以多普勒测速值为真值，以1.5 m/s为粗差检验的阈值进行统计，统计结果如表3所示。

表2 动态试验测速精度统计Tab.2 Speed measurement accuracy of dynamic experimental table mm/s

表3 动态试验测速粗差统计Tab.3 speed measurement gross error of dynamic experimental table %

由表2 动态试验测速精度统计可知，历元星间差分的测速方法明显优于位置差分的测速方法，特别是在垂直方向上。由表3可知，历元星间双差的方法抗环境干扰能力明显优于RTK位置差分的方法。

4 结 论

本文提出了历元星间双差的测速方法，并且进行了静态和动态试验。通过与RTK位置差分和多普勒测速方法进行对比，研究了该方法的测速性能和特点，得出以下结论。

(1)静态并且观测环境较好的条件下，历元星间双差的测速方法精度最高，多普勒的测速方法精度最差。由此可知，在观测环境较好的条件下，历元星间双差的观测噪声最小，E，N，U方向的测速精度分别为3.5，3.8，8.7 mm/s。因此，在观测环境较好并且对精度要求较高的条件下，可以采用历元星间双差的方法进行高精度的速度测量。

(2)动态条件下且存在树木及高楼遮挡的环境下，历元星间双差的测速方法测速精度优于RTK位置差分的同时，显著减少了粗差个数，提高了测速结果的稳定性。但是与多普勒的测速方法相比，历元星间差分的测速方法在测速精度和抗环境干扰能力明显较差。因此，在动态条件下观测环境较差时，应优先采用多普勒的测速方法，但在缺少多普勒观测值时，可以采用历元星间双差的方法取代RTK位置差分的方法。

(3)由于多普勒观测噪声较大，因此，在观测条件较好并且接收机采样频率较高的条件下，历元星间双差的测速方法可以取得比多普勒测速方法更加准确的测速信息。这是由于历元星间双差模型通过引入模糊度参数并对其固定，有效地减少了观测噪声的影响。