DP590带钢屈服和抗拉强度的微磁定量预测

王贤贤,何存富,刘秀成

(北京工业大学 机械工程与应用电子技术学院, 北京 100124)

DP590双相钢(由铁素体和马氏体组成)具有低屈强比、高初始加工硬化率、良好的强度和延性配合等特点，在汽车车身结构件、加强件、防撞件的制造中得到广泛应用[1-2]。带钢性能(如屈服强度、抗拉强度等)是产品质量检验的重要内容。目前主要采用抽样有损方法对带钢性能进行测试，但该方法难以实现带钢性能的在线、快速评价。SJOGREN等[3]发展了带钢性能的微磁无损检测技术，并集成至带钢生产线，用于多项性能的在线评价。

国内在微磁无损检测技术方面的研究主要集中于单一性能指标评价。高铭等[4]利用磁巴克豪森噪声(Magnetic Barkhausen Noise,以下简称MBN)对Q235钢中的应力进行检测，并分析了MBN不同频带成分对应力沿深度分布的表征。陈洪恩等[5]基于增量磁导率方法对碳素钢塑性变形进行无损评价，研究发现，涡流阻抗信号实部值随塑性应变的增大而整体增大，虚部值随塑性变形的增大而整体减小。LUO等[6]研究利用MBN对材料表面硬度进行检测，结果表明,MBN蝶形曲线峰值随表面硬度增大呈减小趋势，峰值对应的切向磁场强度与表面硬度呈现正相关关系。目前，国内尚没有利用微磁方法对双相钢强度指标(屈服强度、抗拉强度)进行定量检测的研究报道。

文章以DP590双相钢为例，利用自主研制的微磁传感器及检测装置，开展双相钢强度指标(屈服强度、抗拉强度)的同步定量预测方法研究。首先，进行试样制备和标定(微磁和拉伸)测试；其次，分析强度指标取值变化对切向磁场强度信号、磁巴克豪森噪声等多项特征参量的影响规律；最后，研究利用多元线性回归模型描述多项磁参量与强度性能指标的关联，并对模型精度进行外部校验。

1 试件制备与拉伸试验

试验选用某钢厂提供的厚2 mm的DP590热轧钢板，在平行轧制方向切取10个长方形试件，尺寸为长200 mm、宽20 mm。依照表1的工艺参数，对试件进行两级退火热处理。

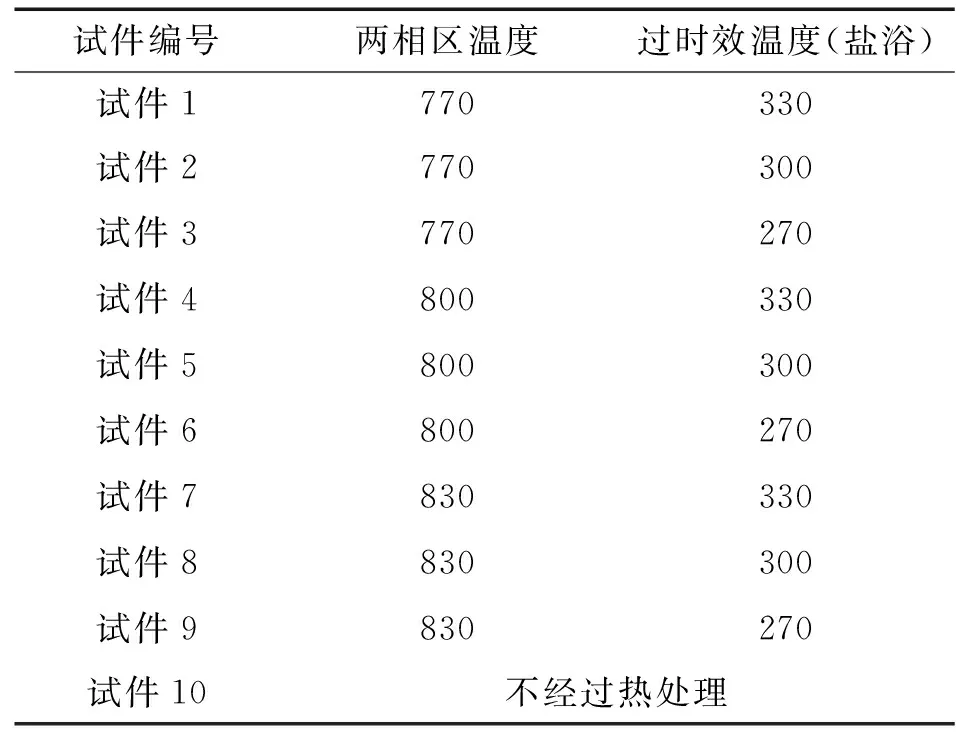
表1 试件正交试验方案 ℃

采用正交试验方案，选取两相区温度、过时效温度这2个对组织性能影响较大的工艺参数为试验变量。其中两相区温度选取770,800,830 ℃3个水平，过时效温度选取270,300,330 ℃3个水平，进行2变量3水平正交试验。其他工艺参数为两相区保温时间20 min，过时效保温时间20 min。过时效保温后空气冷却至室温。

依据国标将热处理后的毛坯试样加工成标准拉伸试件，其尺寸如图1所示。平板拉伸试件标距为50 mm，利用万能电子拉伸机对试件进行拉伸试验，测得的典型应力-应变曲线如图2所示。对所有试件进行测试，估算得到的屈服强度Rp0.2，抗拉强度Rm如表2所示。

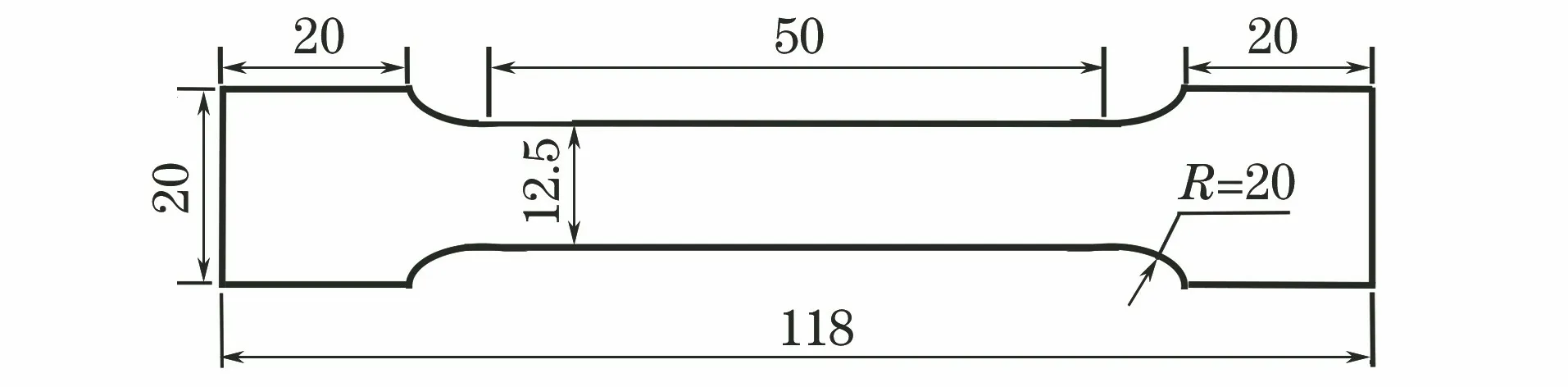
图1 拉伸试件尺寸

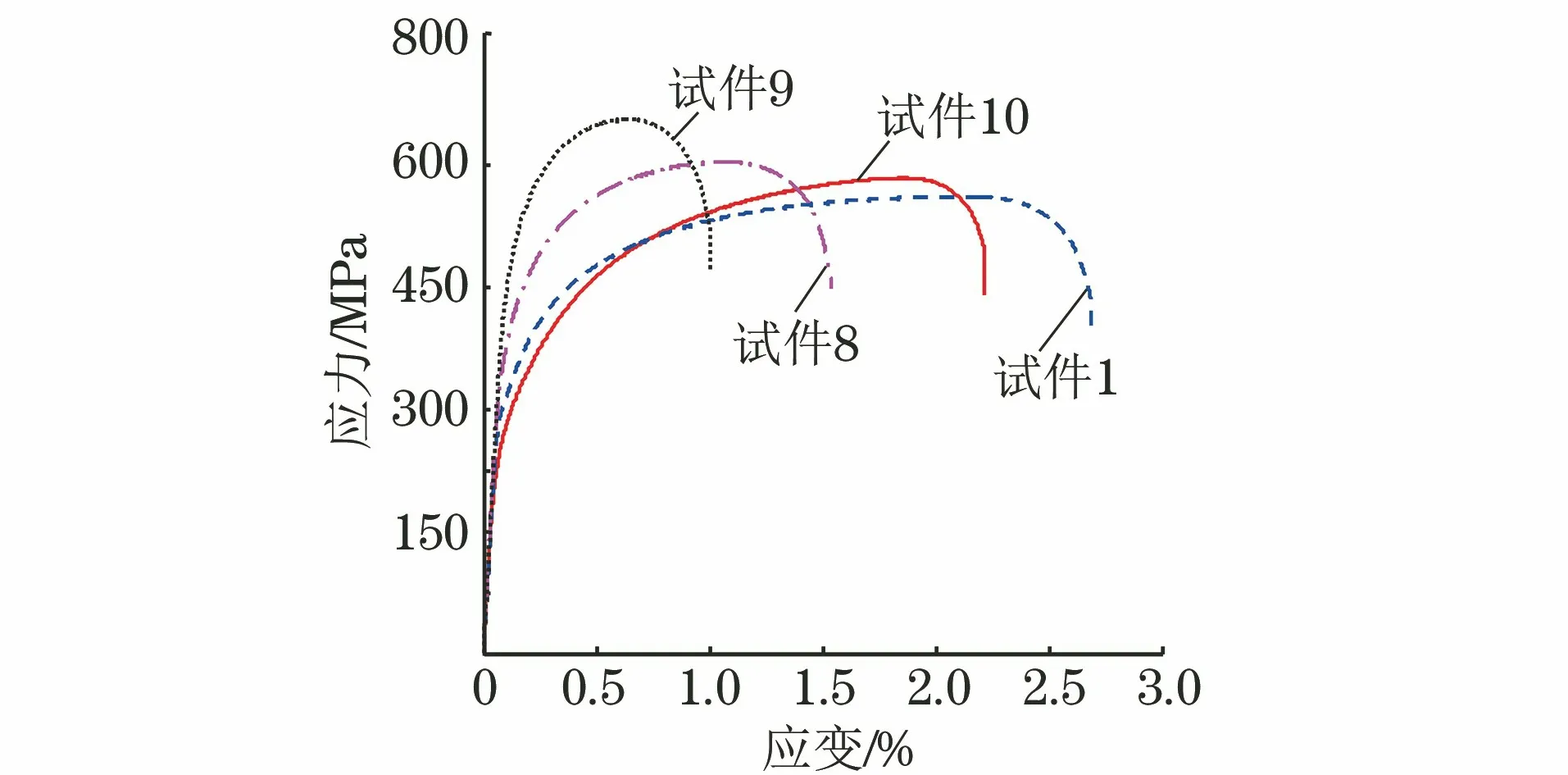
图2 不同试件的应力-应变曲线

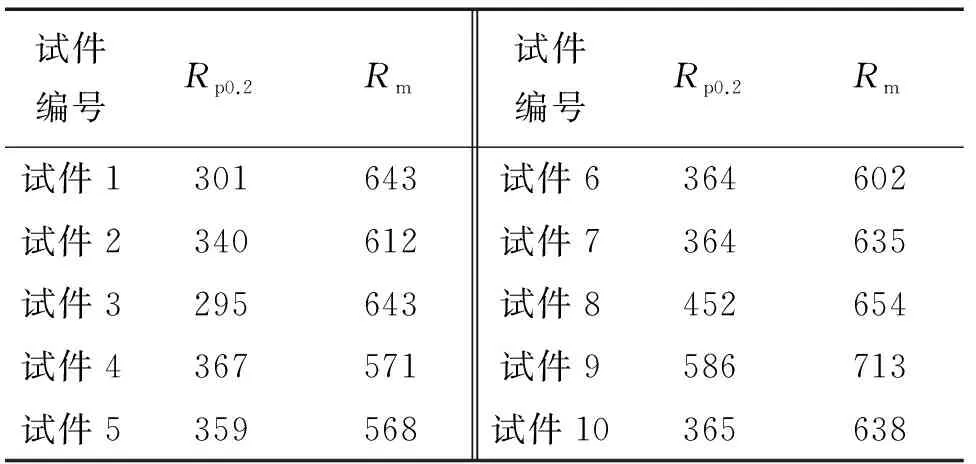
表2 试件的力学性能参数 MPa

2 微磁检测与信号分析

2.1 检测原理

微磁信号主要指铁磁性材料在交变磁化过程中，内部磁畴及其畴壁运动引起的局域化磁扰动信号。磁巴克豪森噪声[7]是典型的微磁信号，主要诱发机制是磁畴及其畴壁运动受位错、晶界等微观结构的钉扎作用而呈现的不连续跳变行为。一方面，磁巴克豪森噪声信号特征与微观结构及其应力状态直接相关[8-9]；另一方面，材料的强度性能也主要由微观结构及其应力状态决定。因此，通过测量微磁性能可以间接表征材料的强度性能。利用微磁方法检测材料的强度指标，重要前提是通过试验标定方法确定材料强度与微磁特征参量间的关系。要确定这一关系，需从微磁参量的选取、关系建模方法等方面进行研究。

2.2 试验系统

文章研制的传感器可同步检测试件表面切向磁场强度及磁巴克豪森噪声两类磁信号。传感器由磁轭、励磁线圈、检测元件(感应线圈和霍尔元件)构成。硅钢叠片构成的U型磁轭两末端加工成锥台，可使磁路与被测试件间以近似点接触方式耦合，顶端绕制的励磁线圈共250匝(线径为0.35 mm)。霍尔元件型号为霍尼韦尔SS39E，其动态工作范围为±1 000 Gs，灵敏度为1.4 mV·Gs-1。感应线圈外径为5.4 mm，内径为2 mm，线径为0.15 mm，高度为9 mm，匝数约为1 200匝。线圈中心内嵌高度为9 mm，直径为2 mm的锌锰铁氧体磁芯。霍尔元件和感应线圈分别检测切向磁场强度的时变信号H(t)及MBN信号。

试验系统由PXI 机箱(内置信号发生卡、数据采集卡)、双极性功率放大器BOP100-4ML、双极性电源、微磁传感器和基于LabVIEW 的控制与分析软件构成(见图3)。信号激励卡产生的幅值为1 V，频率为200 Hz的正弦信号，经过双极性功率放大器放大后通入激励线圈，磁轭末端与试件表面接触后，试件在交变磁场的作用下磁化。检测元件接收的切向磁场时变信号及巴克豪森噪声信号被多通道采集卡采集。硬件对信号的激励与采集均由上位机控制。

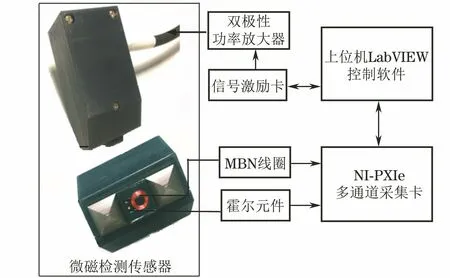
图3 试验系统结构框图

2.3 信号分析

微磁检测易受材料剩磁状态等因素影响，为确保试验结果的稳定性，每次测量前利用交流退磁器对试件进行退磁处理，并前后分5 d进行5次重复性测量。试验测量过程中，双极性电源的电流放大信号保持一致，激励信号为正弦波(频率为200 Hz、幅值为1 V)，信号采样频率为1 MHz，采样时长为1 s。

利用霍尔元件检测试件表面的切向磁场信号，不同热处理工艺的试件的切向磁场幅值不同。在外加交变磁场由正到负的变化过程中，磁场变化涵盖了整个磁化周期的磁学信息，可通过提取磁场变化中的特征值表征试件的力学性能。

切向磁场强度时变信号波形受被测试件中磁滞特性的影响。以未经热处理试件(试件10)的检测结果为基准，不同试件检测的H(t)与基准信号的差值曲线如图4所示。

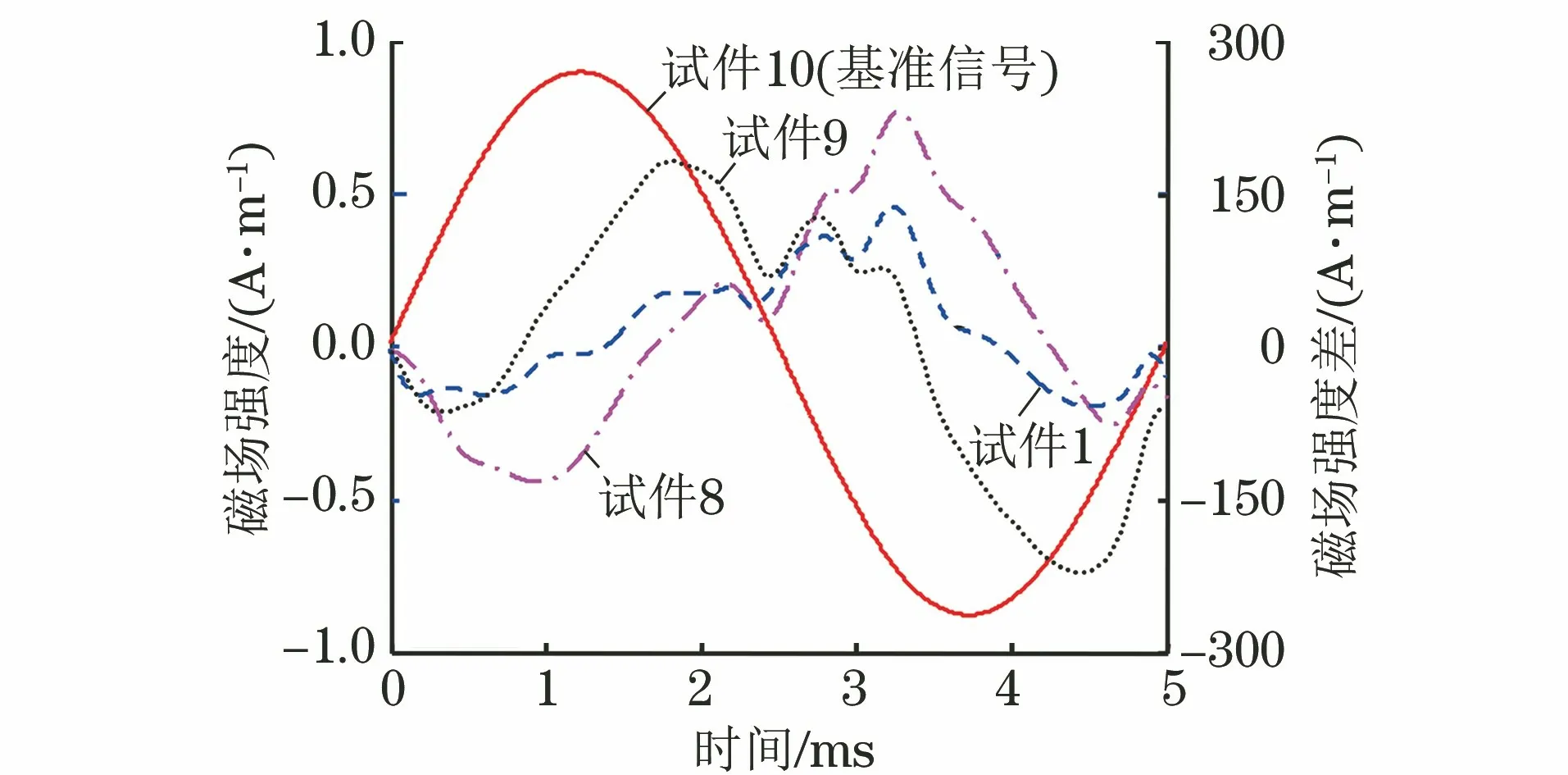
图4 不同试件的H(t)与基准信号的差值曲线

由图4可以观察得到，不同试件中的H(t)波形存在差异，一般选择在频域内对H(t)进行分析，提取基波分量，并计算总谐波畸变因子[10]等，提取的磁参量及其变异系数如表3所示(表中Mmax为MBN包络线的最大值，为方便表示，用各符号变量表示磁参量)。

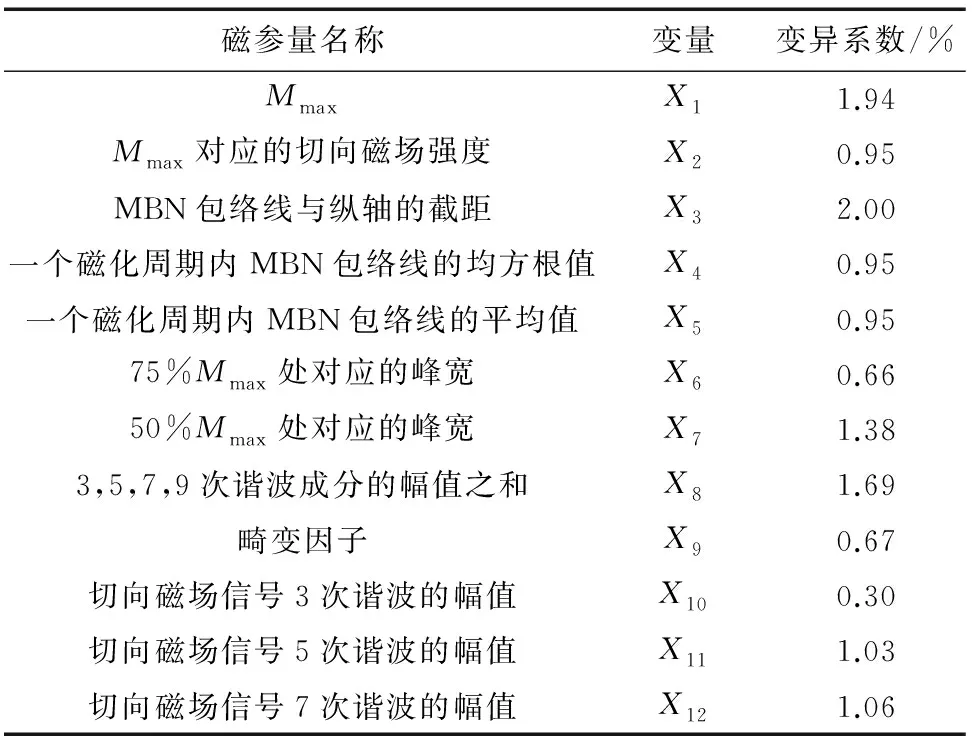
表3 提取的磁参量及其变异系数

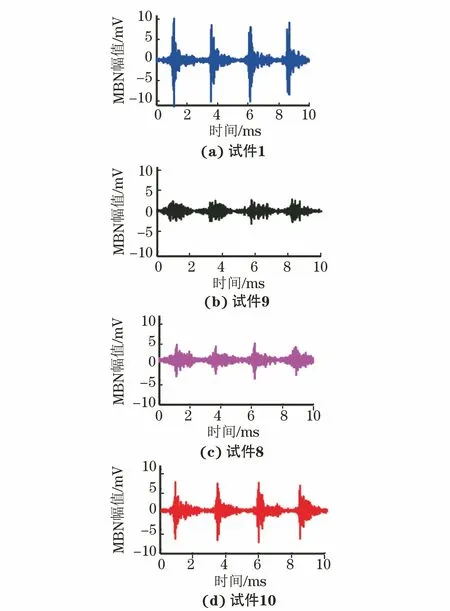
图5 不同试件的磁巴克豪森噪声信号

不同试件中检测得到的MBN信号如图5所示，可以发现，MBN信号波形及峰值均受材料热处理(本质是微观结构变化)影响。为提取MBN的特征参量，将接收线圈检测到的信号进行带通滤波，选用巴特沃斯滤波器，上、下截止频率分别为20,40 kHz。从带通滤波得到的MBN信号中截取150个周期进行滑动平均，得到MBN包络线，再求出150个周期中单个励磁周期内的MBN包络线随H(t)的变化轨迹，绘制蝶形曲线。不同试件的蝶形曲线如图6所示，可见，不同试件的MBN蝶形曲线形状也不同，即蝶形曲线形状也可以作为试件强度的敏感参量。从绘制的蝶形曲线中，提取X1，X2,X6,X7等特征参量，用以表征材料的强度指标。

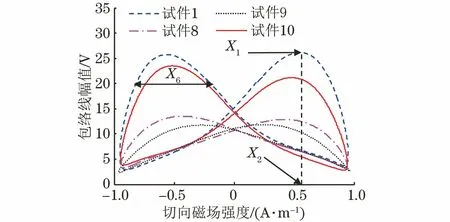
图6 不同试件的蝴蝶曲线

为评价检测装置的性能，利用变异系数分析方法对磁参量重复检测。选取未经热处理的10号试件为例，对5 d分别测得的H(t)和MBN参量进行变异系数统计(结果见表3)。由表3可见，该检测装置测得的磁参量变异系数均小于2%，具有较好的重复性。

3 强度指标的微磁定量预测模型

3.1 多元线性回归分析

利用多元线性回归分析方法，建立如表3所示的磁参量与强度指标的关系方程。关系方程的特征如线性拟合确定系数R2，均方根误差等与方程的自变量(微磁参量)的选取有关。该试验在建模中，选取前4天的数据用于模型训练，第5天的数据用于外部校验，分析模型预测误差。基于逐步回归方法，利用F检验[11-12]从表3所列的12个自变量中筛选出对强度显著影响的特征参量。按照每个待选变量的重要程度(以显著水平表示)，将变量逐次引入回归方程。设置进入模型的参量显著水平为小于0.05。

首先以屈服强度为因变量，将变量逐次引入回归方程，统计得到12个参量的显著水平，结果如表4所示。可以利用参量X2,X3,X4,X8和X11对屈服强度进行多元线性表征。方程式为

YRp0.2=A0+A1X2+A2X3+A3X4+

A4X8+A5X11

(1)

式中：A0=1 029.52；A1=-0.040 3；A2= -23.920 1；A3=-0.023 5；A4=-8 723.86；A5= 3.276 1。

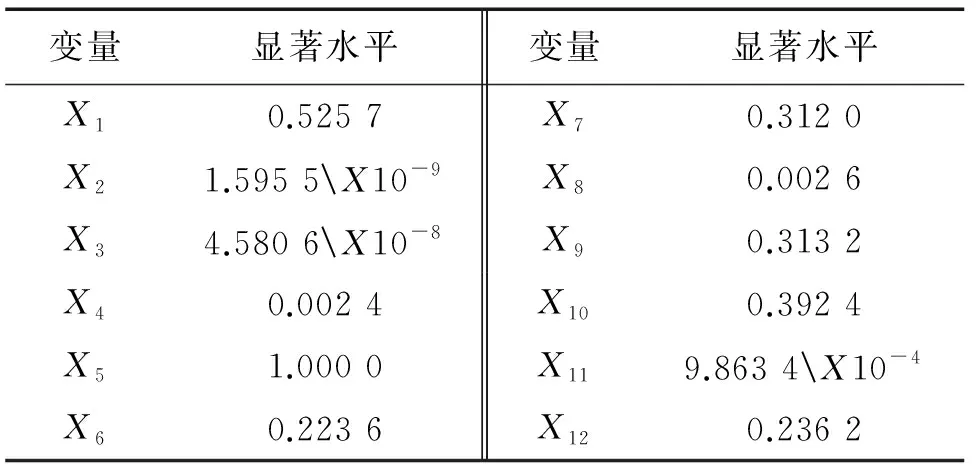
表4 磁参量的显著水平分析结果

式(1)的线性拟合确定系数R2为0.932，均方根误差为20.66。将外部校验数据代入式(1)对屈服强度进行定量预测，预测结果如图7所示，其平均误差为5.03%，最大误差为13.46%。

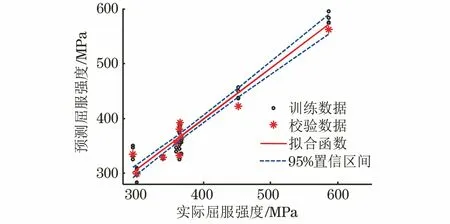
图7 屈服强度的预测结果

同理，以抗拉强度为因变量，将变量逐次引入回归方程，统计得到12个参数的显著水平，结果如表5所示。磁参量X2,X4与抗拉强度的关系可用二元一次方程表征：

YRm=B0+B1X2+B2X4

(2)

式中：B0=837.516；B1=-0.021 6；B2= -0.016 2。

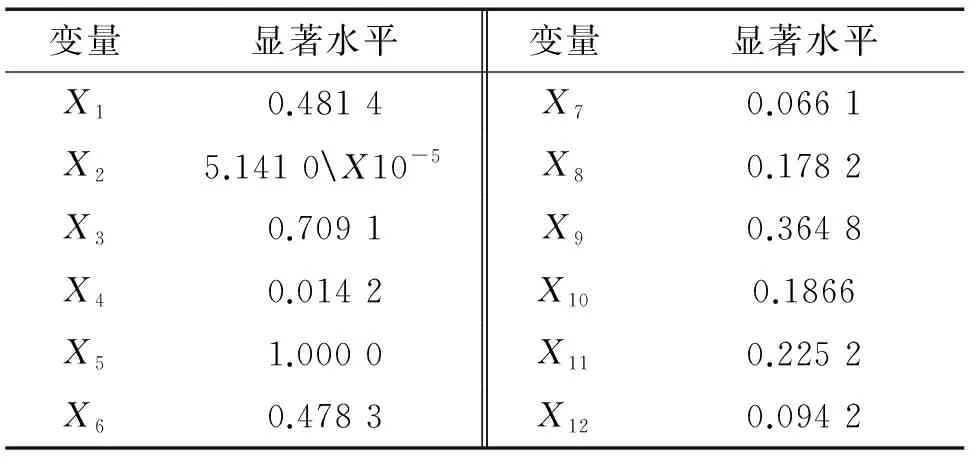
表5 磁参量的显著水平分析结果

式(2)的线性拟合确定系数R2为0.647，均方根误差为19.83。通过外部数据对抗拉强度校验的预测结果如图8所示，其平均误差为3.11%，最大误差为6.25%。

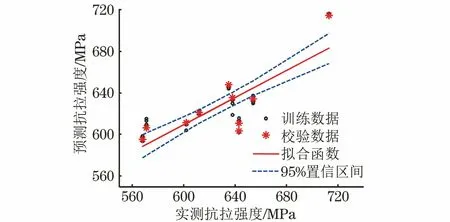
图8 抗拉强度的预测结果

3.2 模型的改进

为改进模型精度，尝试进行多元二次方程式回归分析。其具体步骤与前述多元线性回归方程一致，只是模型自变量输入有所变化。将表3所列12个参量进行平方处理后，与原始参量一同作为自变量(共24个)。此时，针对屈服强度和抗拉强度进行的各参量显著水平分析结果分别如表6，7所示。

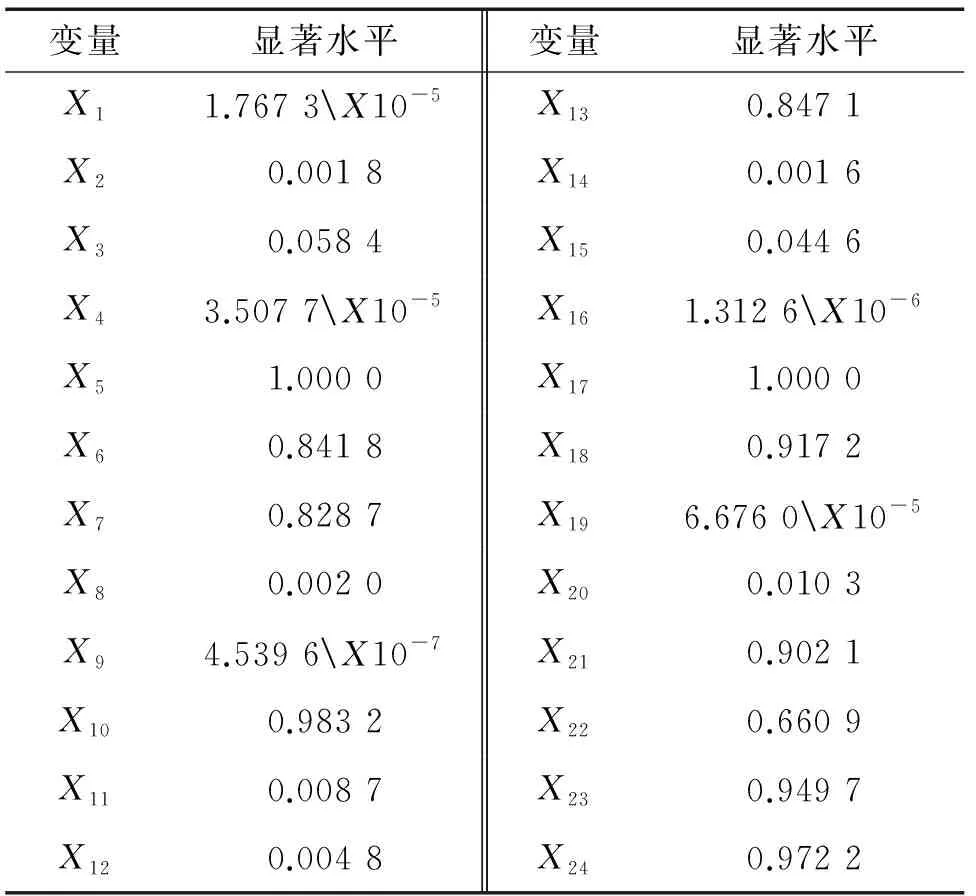
表6 屈服强度对应磁参量的显著水平分析结果

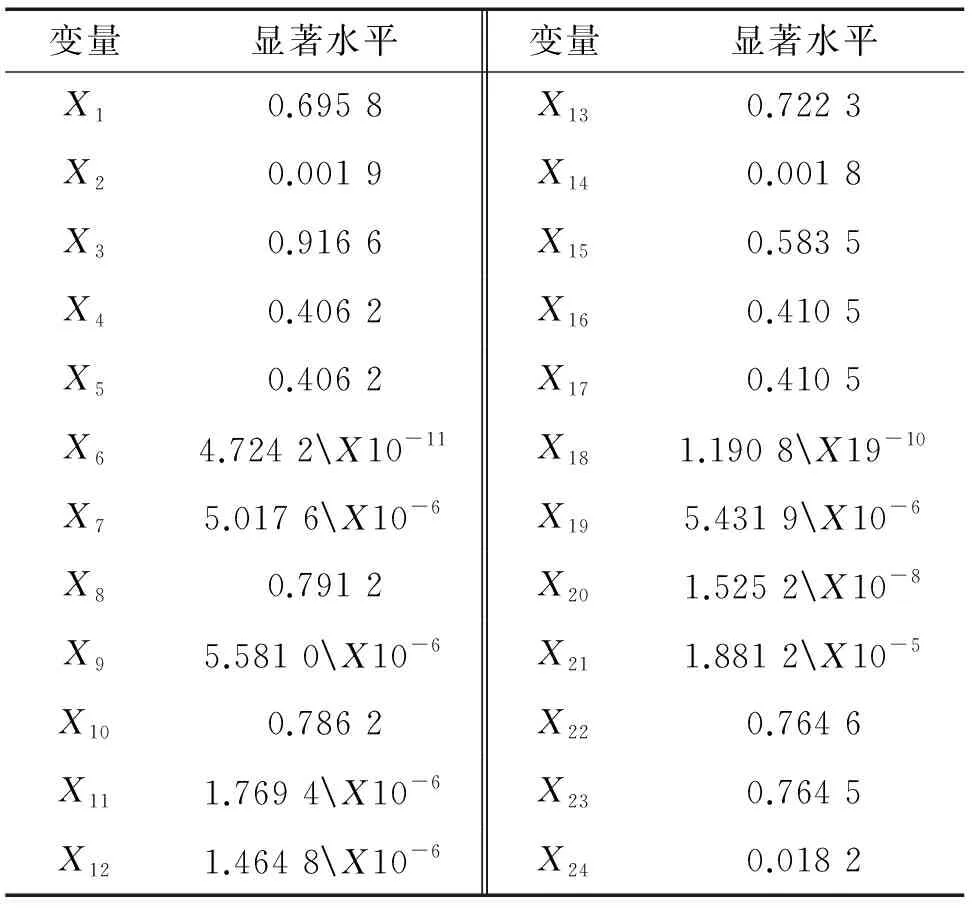
表7 抗拉强度对应磁参量的显著水平分析结果

以屈服强度为因变量，将变量逐次引入回归方程，得到用于描述屈服强度的多元二次方程式

YRp0.2=C0+C1X1+C2X2+C3X3+C4X4+

C5X8+C6X9+C7X12+C8X13+C9X15+

C10X16+C11X17+C12X20+C13X21

(3)

式中：C0=3 268.03；C1=54.034；C2= -0.308；C3=-84.402；C4=-0.455；C5=-25 430.633；C6=-111 788.403；C7=-2.797；C8=-5.121；C9=2.890；C10=3.236；C11= 4.336；C12=0.024；C13= -2 225 138.76。

式(3)线性拟合确定系数R2为0.994，均方根误差为6.49。将外部校验数据代入方程后的预测结果如图9所示，其平均误差为2.93%，最大误差为7.51%。

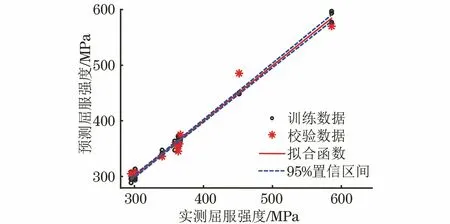
图9 模型改进后屈服强度的预测结果

同理，以抗拉强度为因变量，用于描述抗拉强度的方程式为

YRm=D0+D1X2+D2X6+D3X7+D4X9+

D5X12+D6X13+D7X15+D8X19+D9X20+

D10X21+D11X22+D12X26

(4)

式中：D0=280.529；D1=0.095；D2= -0.203；D3=-3.089；D4=111 943.762；D5=5.98;D6=15.903；D7=-9.588；D8=1.549；D9=-0.029;D10=6 060 227.509；D11= -3 961 766.523；D12= -0.309。

分析抗拉强度的多元二次线性拟合方程式(4)，其线性拟合确定系数为R2为0.976 8，均方根误差为6.24。将外部校验数据代入式(4)对抗拉强度进行定量预测，结果如图10所示，其平均误差为1.13%，最大误差为3.16%。

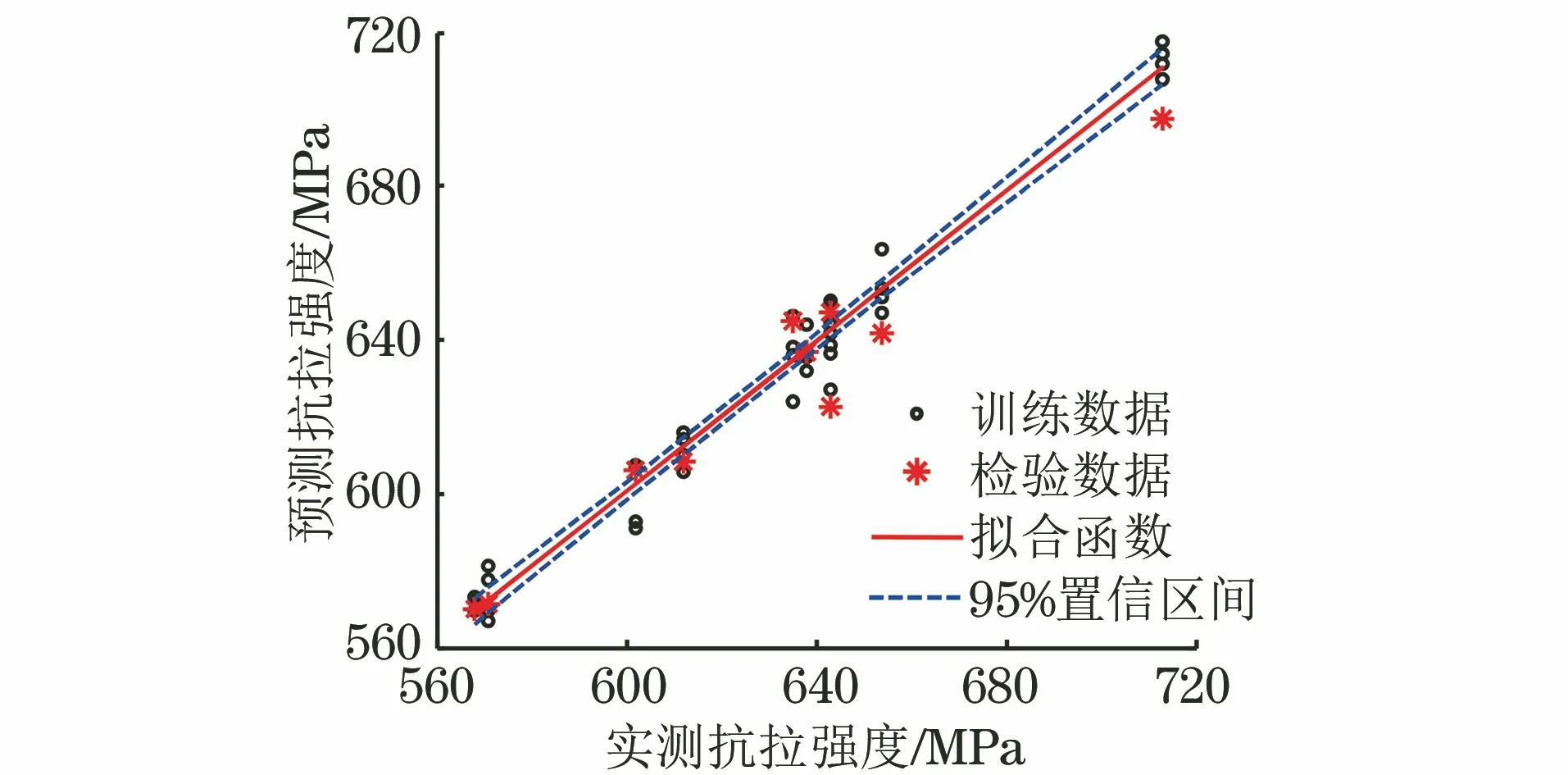
图10 模型改进后抗拉强度的预测结果

4 结论

(1) 构建的试验系统对磁参量的重复测试性能优异。磁巴克豪森噪声与切向磁场强度的多项磁参量重复测试结果的变异系数均小于2%。

(2) 在分析的所有磁参量中，Mmax对应的切向磁场强度是材料强度指标的重要表征参数。在建立的屈服强度和抗拉强度的多元线性回归定量预测模型中，其显著水平分析结果均小于0.05。

(3) 材料强度指标的定量预测精度与模型输入参数有关，多元二次方程回归模型相较于多元一次方程回归模型的预测精度更高。