基于PWM技术的大型变量喷灌机整机水力性能研究及优化

莫锦秋，黄小林，李文涛，李彦明

基于PWM技术的大型变量喷灌机整机水力性能研究及优化

莫锦秋，黄小林，李文涛，李彦明

（上海交通大学机械与动力工程学院，上海 200240）

基于脉冲宽度调制（Pulse Width Modulation, PWM）技术的变量喷灌机虽然能实现更精细的地块水分管理，但因实现变量的电磁阀的持续开闭动作，喷灌机主输水管道内流量呈现持续的阶跃变化，进而导致变量喷灌过程中存在压力脉动和机械激振现象。该研究基于Matlab/Simulink，对基于PWM技术的大型变量喷灌机在变量喷灌过程中的压力脉动进行了研究分析及改善优化。针对已研制的基于PWM技术的大型变量喷灌机实体系统，首先构建了其关键器件和整机的水力模型，并验证了模型的正确性。然后基于所建模型，对变量喷灌机的压力脉动进行了分析，得到了变量喷灌过程中的压力脉动规律，进而提出了PWM脉冲相位错开的缓减方法，并介绍了该方法的3种具体实施方式，即“站间”错相、“站内”错相和“站间+站内”错相。最后在实现了PWM脉冲相位错开的变量喷灌机整机水力模型上进行仿真分析，证明了所提3种错相方式均可明显减小变量喷灌过程中的压力脉动幅度，同时也可有效提高泵站的利用率。此外，通过在实现了PWM脉冲相位错开的变量喷灌机实体系统上开展田间试验，进一步验证了所提PWM脉冲相位错开方法对于缓减压力脉动和机械激振的有效性。且田间试验结果表明，在采用PWM脉冲相位错开方法时，变量喷灌机仍然具有较好的喷洒均匀性和变量灌溉控制误差。该研究成果不仅能为基于PWM技术的变量喷灌提供较平稳的压力条件从而保障变量喷灌控制精度，还能减小因压力脉动引起的机架激振从而保障设备安全。

模型；压力脉动；大型喷灌机；变量喷灌；脉冲宽度调制

0 引 言

传统喷灌系统在大面积农田中只能进行均匀灌溉，为了提高水分生产率和水资源利用率，实现以农田各小区域内具体作物的实际需水量为导向的按需精准喷灌，变量喷灌应运而生[1-5]。变量喷灌主要是通过行走速度控制和定点实时调节各喷头流量来达到变量的目的，而在实现喷头流量调节的众多方法中，基于脉冲宽度调制（Pulse Width Modulation，PWM）技术的变量控制是目前的主流研究与实施方法[6-9]，该方法通过改变PWM脉冲信号的占空比来控制各喷头前端电磁阀的开启时间比例，从而实现对各喷头喷洒水量的独立控制。但目前国内外基于PWM技术的变量喷灌相关研究文献均未给出整机上各喷头的PWM相位关系。当简单地采用整机所有喷头相同PWM相位时，全体电磁阀的持续同相位同周期的开闭会使得主输水管道压力产生大幅的周期性脉动，并引起机械激振[10]。由于基于PWM技术的大型变量喷灌机（后文简称大型PWM变量喷灌机）输水管路长、整机喷头众多、PWM周期为10 s量级[10]，上述压力脉动无法由供水系统的压力反馈控制来减小。过大的主输水管压力脉动会改变喷头瞬间流量，鉴于PWM变量喷灌基于确定的喷头瞬间流量按不同通水占比来实现流量控制的机理，主输水管压力脉动将极大影响变量控制的精度。因此求取大型PWM变量喷灌机在变量喷灌过程中的压力脉动规律并寻求压力脉动缓减措施是实现准确PWM变量喷灌的前提。

目前对于喷灌机的水力性能相关研究中，多是均匀灌溉时的定常计算或是对单一部件的水力性能研究。如刘忠潮等[11-14]对喷头等间距分布和不等间距分布情况下的基于多口系数的喷灌机管道压力计算方法进行了研究。Kincaid等[15]研究了圆形喷灌机在定常流动下的压力分布情况。基于多口系数的计算方法相当于采用折算系数的估算方法，结果相对粗糙。而在单一喷灌部件的水力性能相关研究中，张云龙等[16]应用计算流体力学方法对圆形喷灌机系统两井泵汇流装置进行了研究，求取了雷诺数与两进口汇流比，以及汇流装置的总水力损失与两进口局部阻力系数之间的关系。张琛[17]采用理论分析和数值模拟方法对压力调节器的设计和性能优化进行了研究，为压力调节器的设计与改进提供了理论和技术支撑。上述研究均是针对部件的分析，并未揭示喷灌机整体相互作用下的水力特性。

由于变量喷灌过程中压力脉动的时间相关性，所以动态性能分析显得十分必要。但传统的流体系统动态分析方法多是基于流体方程的数值求解，变量繁多，过程抽象且易出错[18]。而基于Matlab/Simulink的建模仿真具有建模简便直观、计算迅速准确、可根据需要灵活自定义组件等优势[19]，且其工具包Simscape内即有成熟的针对流体分析的组件。

本文针对已研制的大型PWM变量喷灌机实体系统，首先对其关键器件的水力模型进行构建，进而建立整机水力模型，并结合试验验证模型的正确性。基于所建模型，对PWM变量喷灌过程中的压力脉动进行分析，拟根据脉动规律寻求缓减措施，并结合田间试验验证其有效性。

1 PWM变量喷灌机水力模型构建与验证

1.1 试验系统及方法

1.1.1 试验系统

研制的位于河南许昌基地的大型PWM变量喷灌机实体如图1，该变量喷灌机同时具备平移变量喷灌作业和旋转变量喷灌作业功能，其主输水管道由主塔车和节点塔车支承。

1.主塔车 2.主控制器 3.喷灌机进水口 4.喷洒执行件 5.主输水管道 6.电磁阀 7.出水分管道 8.第1跨 9.1#节点控制器 10.2#节点控制器 11.节点塔车 12.第2跨 13.3#节点控制器 14.第3跨 15.4#节点控制器 16.第4跨 17.5#节点控制器

在结构上，此喷灌机共4跨（从主塔车端开始依次为第1、2、3、4跨），无尾枪，主塔车端进水，每跨50 m，在各跨主输水管道上间隔3 m设置出水口，各出水口后接电磁阀，然后接鹅颈弯管和软管，软管末端则是压力调节器和喷头（本文合称喷洒执行件）。整机共75个喷头，基于分级分布式控制[10]，每个喷头的喷洒受控于其上方电磁阀的开闭，而各电磁阀分别由离其最近的位于各节点塔车上的节点控制器独立控制，整机共有5个节点控制器（从主塔车端开始依次为1#、2#、3#、4#、5#节点控制器），每个节点控制器均可独立控制16路电磁阀（5#节点控制器例外，仅控制11路），同时每个节点控制器均受位于主塔车上的主控制器控制。另外，该变量喷灌机由3泵并联的远程水源供水系统抽取地下水来供水，且在喷灌机进水口和各跨前后端的主输水管道上安装了压力表（红旗YTN-100，量程0.6 MPa），在喷灌机进水口处安装了压力传感器（星仪CYYZ11，量程0.6 MPa，输出信号0～20 mA），均为竖直安装，压力传感器与主控制器内STM32开发板（STM32 F103R8）的模拟输入通道相连（外加采样电阻165 Ω，使0～20 mA电流模拟量转换为0～3.3 V电压信号后进行12位、4 Hz AD采集），采集数据在主控制器处经串口通信送达变量控制主机。

1.1.2 试验方法

1）喷头流量

在大型PWM变量喷灌机实体系统上任取5个喷头作为试验喷头，并去掉喷头挡水盘，分别设置系统压力、PWM周期和PWM占空比后，在喷头下方放置水桶，测量所有试验喷头在此条件下的2 min出水量。当完成所有喷头测量后，先将所有试验喷头出水量测量值取平均，再结合集水时长计算喷头流量。

2）喷灌机各部分压力损失

在大型PWM变量喷灌机实体系统上分别设置系统压力、PWM周期和PWM占空比后，进行田间静态喷洒试验，待系统压力稳定后，通过读取位于各跨前后端的压力表示数，求差得到所设条件下的喷灌机各部分压力损失。

1.2 关键器件水力模型构建

变量喷灌机的关键水力器件从结构上按照功能或流阻特性可拆分为组件。针对各组件，根据其特性，可直接采用Simscape工具包内已有的成熟组件(或组件的组合)进行描述，或按照组件特性表达式自定义Simscape组件模块来描述。

1.2.1 输水管道

从结构上看，喷灌机的主输水管道和各出水分管道可切分为直管结构、弯管结构和T型三通分水管结构。对于直管结构，本文使用Simscape中的“Resistive Pipe LP”模型，描述该模型流阻特性的为达西公式[20]。对于弯管和T型三通分水管结构，分别采用Simscape中基于局部阻力块模型封装的“Pipe Bend”模型和“T-junction”模型。

1.2.2 喷洒执行件

变量喷灌机喷洒执行件包含压力调节器和喷头，本文PWM变量喷灌机实体所用喷头为美国尼尔森公司的Nelson D3000喷头，由3TN系列喷嘴和档水盘等组成。Nelson D3000喷头在压力一定时，不同型号的喷嘴因孔口直径不同而瞬间通水流量不同。其中，压力调节器是保证整机所有喷嘴入口压力相等且为定值的关键器件。本文所用压力调节器为美国尼尔森公司Nelson D3000喷头配套的Nelson压力调节器，按Nelson压力调节器的产品使用技术要求，因压力调节器内部摩擦损失，要求设计时入口压力应当比出口要求压力高0.035 MPa，即：

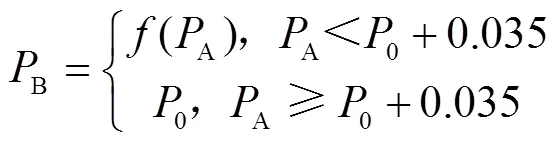
基于（1）式，使用Simscape模块编程语言自定义压力调节器模型。对于具体型号的喷嘴，将视作截面积固定的孔口，可直接使用Simscape中的“Fixed Orifice”模型。

1.2.3 电磁阀

电磁阀是实现变量喷灌的关键器件，本文变量喷灌机实体所用电磁阀为直流24 V直动式膜片常闭电磁阀，选用开灵的2W200-20型号。根据其动作机理，采用Simscape中“2-Position Valve Actuator”（二位阀执行器）模型与“2-Way Directional Valve”（二通换向阀）模型的组合来进行建模。其中二位阀执行器接收来自节点控制器的PWM脉冲信号，并根据信号幅值驱动二通换向阀进行状态切换。此模型可保证电磁阀的开启（或关闭）过程包含加速（或减速）和匀速阶段，且开启和关闭耗时长短可根据电磁阀自身开关特性进行设定。

1.2.4 水源供水系统

本文变量喷灌机实体系统由3泵并联供水，各泵站均由1个变频器和1个深井泵构成。深井泵为定排量泵，其出水流量取决于电机转速。而变频器参考该泵站设定的目标压力值，根据反馈压力，采用PID（Proportion Integration Differentiation）控制律来不断调整深井泵电机的供电频率，进而改变泵站的出水流量，以使压力采集点（泵站出水口）的压力在一定范围内相对稳定。水源供水系统的输出总流量可表示为

根据泵站构成，采用Simscape中“Velocity Source”（速度源）模型与“Fixed-Displacement Pump”（定排量泵）模型的组合来建立深井泵模型，其中速度源相当于深井泵电机，其转速由PID输出的交流电频率决定，而PID参数取值则与实体系统相同。

1.3 喷灌机整机水力模型构建

喷灌机主输水管道为在主塔车处竖直上升、在各跨形状均呈拱形的镀锌钢管。首先将主输水管道拆分为直管、90°弯管和T型三通分水管结构，将各出水分管拆分为鹅颈弯管和分管直管结构。然后结合关键器件模型，分别构建喷灌机各跨水力模型及水源供水系统和主塔车管道水力模型，如图2a和图2b所示（此处仅以第2跨为例来介绍本文大型PWM变量喷灌机各跨水力模型构建结果，其他跨模型类似）。最后将水源供水系统模型、主塔车管道模型、各跨模型顺次连接，同时创建可设置PWM周期及占空比等参数的各个节点控制器，以在仿真过程中按需生成控制各路电磁阀开闭的PWM脉冲，并参照实体系统，建立各节点控制器与各路电磁阀之间的具体信号连接，从而构建出针对已研制的大型PWM变量喷灌机实体系统的整机水力模型，结果如图2c所示。根据图1的喷灌机实体系统实际配置，相关参数取值如表1所示。

表1 模型构建相关参数取值

注：Vx_y为节点控制器x连接到其控制的各路电磁阀的输出端口，x为节点控制器序号，y为端口序号，其中：x=1,2,…,5；y=11,12,…,18,21,22,…,28。

Note: Vx_y is the output port of the node controller x connected to each solenoid valve controlled by it, x is the serial number of the node controller, y is the serial number of the output port, where: x=1,2,…,5;y=11,12,…,18,21,22,…,28.

图2 变量喷灌机整机水力模型构建

<

Fig.2 Construction of hydraulic model of the variable sprinkler irrigation machine

1.4 喷灌机水力模型验证

1.4.1 喷洒执行件和电磁阀水力模型验证

基于已建立的喷洒执行件模型，得到单一喷洒执行件在不同压力调节器入口压力下的喷头流量。如图3a所示，当压力调节器入口压力达到其设计入口压力值后，压力调节器进入正常调节状态，此时喷头流量随压力调节器入口压力的恒定而稳定。

再结合已建立的电磁阀模型，保持压力调节器入口压力值为不低于其设计入口压力的0.20 MPa、PWM周期为变量喷灌作业常用的10 s，得到单一喷头在不同PWM占空比下的出水流量，如图3b所示，可看出喷头出水流量在变量区（PWM占空比低于100%）与PWM占空比有较好的线性关系，但均偏离由100%占空比时喷头出水流量计算所得的理论值，而偏离程度由电磁阀自身的开关特性所决定。

在与仿真相同条件下，根据喷头流量获取方法，在变量喷灌机实体系统上进行试验，测得了不同设置下的喷头流量。图3a和图3b中试验值与仿真值吻合，说明了所建喷洒执行件模型和电磁阀模型的合理性。

1.4.2 整机水力模型验证

参考变量喷灌作业常用压力，取泵站目标压力值0.25 MPa，在整机100%PWM占空比下，仿真获取了此时喷灌机主塔车和各跨的压力损失，如图3c，可看出喷灌机压力损失主要发生在主塔车处（约0.037 MPa），各跨压力损失从第1跨到第4跨逐渐减小。

在研制的大型PWM变量喷灌机实体系统上按照仿真相同设置进行静态喷洒，根据喷灌机各部分压力损失获取方法，得到了相同条件下的喷灌机各部分压力损失，与仿真值相近（图3c），从而验证了所建整机水力模型的合理性。

图3 关键器件与整机水力模型验证

2 PWM变量喷灌机压力脉动分析及改善

2.1 压力脉动分析

因大型PWM变量喷灌机田间喷灌作业时行走速度较低，经田间实践发现，行走对喷灌机压力脉动的影响不大，故对大型PWM变量喷灌机的压力脉动研究与改善过程中的相关仿真与试验均在变量喷灌机静止状态下进行。且在变量喷灌过程中，通过观察位于喷灌机入水口和各跨前后端的压力表示数发现，喷灌机进水口处压力脉动幅度最大，故压力脉动相关仿真与试验的数据采集点均设在喷灌机进水口处。另外，根据文献[21]，取具有较好喷洒均匀性的PWM周期为10 s，参考田间变量喷灌作业常用压力，泵站目标压力值取0.25 MPa。

基于所建立的整机水力模型，先设置整机PWM占空比为具有代表性的50%，得到变量喷灌时的喷灌机进水口压力曲线、以及位于第4跨中间的压力调节器（具有整机最低压力调节器入口压力）的入口压力曲线，如图4，可以看出，在变量喷灌过程中，喷灌机主输水管道内存在压力脉动，且仅发生在电磁阀打开和关闭瞬间，其中打开瞬间压力减小，关闭后瞬间压力增大，增大幅度远高于减小幅度。究其原因，是由于在电磁阀快速打开和快速关闭时，喷灌机主输水管道内存在流量突变，而由于远程泵站采样时间和调整时间的存在，泵站输出流量并不能跟随整机实际喷灌流量的变化而同步变化，即产生的流量突变并不能及时得到泵站的响应，从而导致压力脉动的产生[22]，而且因为采样时间和调整时间的非零性，该压力脉动将一直存在。另外，从图4中的压力调节器入口压力曲线还可看出，由于主输水管道内的压力脉动，在电磁阀开启瞬间存在压力调节器入口压力低于其设计入口压力的时刻，这将导致喷头喷洒流量的偏低以及变量喷灌结果的不准确。

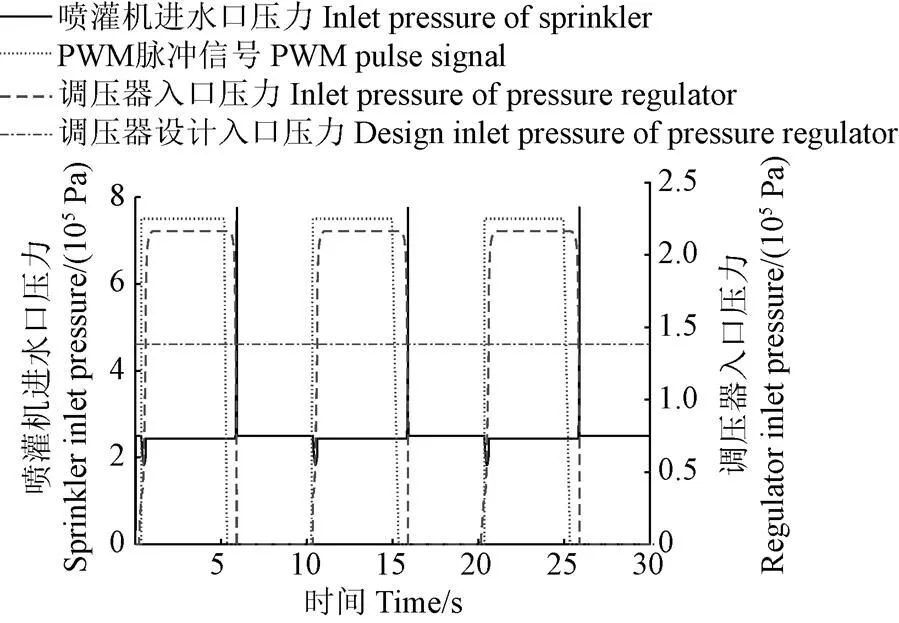
图4 喷灌机进水口压力和调压器入口压力

为了明确在变量喷灌过程中PWM占空比、系统作业压力、变量作业喷头数和供水系统压力调节响应时间等因素对压力脉动幅度的影响，首先获取了在不同系统作业压力水平、不同PWM占空比下的喷灌机进水口压力脉动幅度（即单个PWM周期内喷灌机进水口压力最大值与最小值的差），如图5，可知压力脉动幅度与PWM占空比大小无关，但随着系统作业压力的增大而增大。然后鉴于压力脉动与流量突变的相关性，保持50%PWM占空比不变，得到不同变量作业喷头数下的喷灌机进水口压力最值，如图6，可知变量作业喷头数越多，即流量突变值越大，喷灌机进水口压力最大值越大，压力最小值越小，即压力脉动幅度越大，且压力脉动幅度非线性增大。最后以变化PID积分系数I为例（仅在实体系统实际值0.003周围小量变化），对供水系统压力调节响应时间的影响进行了仿真分析，得到50%PWM占空比时不同PID积分系数I下的喷灌机进水口压力曲线如图7，对比知压力脉动幅度随着I的增大（对应系统响应时间减小）而减小，从而可得压力脉动幅度与供水系统压力调节响应时间成正相关。

最后，取2#节点控制器所控制的16个喷头进行田间变量喷洒试验，其他喷头采用100%PWM占空比。喷灌机静止，设置泵站目标压力为0.20 MPa（该压力在满足整机所有压力调节器入口压力均大于其设计入口压力的前提下，产生的脉动激振幅度适中，对设备造成的机械损伤小）、试验喷头PWM周期为10 s、PWM占空比为50%，待喷洒状态稳定后，通过安装在喷灌机进水口处的压力传感器采集了此时喷灌机进水口压力曲线，并进行中值滤波降噪处理，结果如图8，对比图中的仿真曲线，两者脉动规律基本吻合，从而进一步验证了所建模型和分析的合理性。

图5 不同PWM占空比下的喷灌机进水口压力脉动幅度

图6 不同变量作业喷头数下的喷灌机进水口压力最值

图7 不同PID积分系数KI下的喷灌机进水口压力

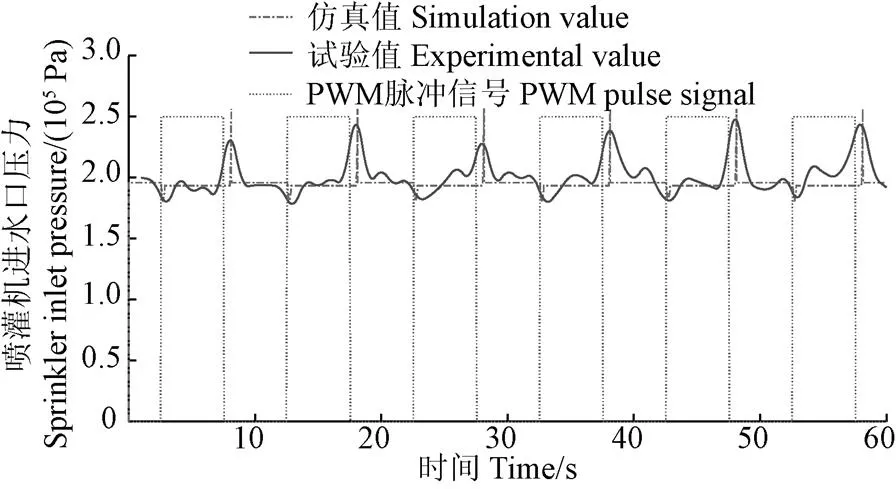
图8 2#节点控制器变量喷灌时的喷灌机进水口压力

2.2 压力脉动改善

变量喷灌过程中的压力脉动不仅会影响喷灌结果的准确性，而且脉动幅度过大时的机械激振易对喷灌机造成致命损伤。因此，对变量喷灌机的压力脉动进行改善是实现准确且安全的变量喷灌的前提。

优化供水系统泵站变频器的压力反馈调节策略，如提高PID调节的系统响应时间、采用自适应PID控制等，理论上可减小压力脉动幅度。但由于水的远程输送时间、压力脉动传输时间及途中损失等因素，供水系统压力调节即使是调整到较理想状态时，对变量喷灌机压力脉动的改善也不明显。

结合压力脉动的产生原因，可通过减小变量喷灌过程中主输水管道内的流量阶跃幅度来缓减压力脉动。即从变量喷灌具体执行策略的角度，在变量喷灌过程中减少同一时刻打开或关闭电磁阀的数量，也就是按一定策略将控制电磁阀开闭的各路PWM脉冲相位进行错开。结合大型PWM变量喷灌机的控制系统构成，若以节点控制器为站，则该方法可具体分为“站间”错相、“站内”错相、以及“站间+站内”错相。

2.2.1 错相方式

1）“站间”错相

以节点控制器为单位，在生成各路PWM脉冲时，同一节点控制器下的各路PWM脉冲相位相同，而不同节点控制器下的PWM脉冲则把相位错开一定角度。错开角度及各节点控制器的PWM脉冲相位可表示为

2）“站内”错相

先将同一节点控制器所控制的电磁阀进行分组并顺次进行编号，不同节点控制器下的对应位置电磁阀组编号相同，然后以电磁阀组为单位，在生成各路PWM脉冲时，相同编号电磁阀组内的各路PWM脉冲相位相同，不同编号电磁阀组的PWM脉冲相位则错开一定角度。错开角度及各电磁阀组的PWM脉冲相位可表示为

3）“站间+站内”错相

综合“站内”错相和“站间”错相，同时考虑节点控制器实现程序的可复用性，首先分别将各节点控制器下的电磁阀按相同规则进行分组，并保证每个节点控制器下所分组数相同，然后将整机所有电磁阀组顺次进行编号，各节点控制器下对应电磁阀组之间编号不同。在生成各路PWM脉冲时，将整机相邻编号电磁阀组间的PWM脉冲相位错开一定角度，而同一电磁阀组内的各路PWM脉冲相位则相同。其中，错开角度及各电磁阀组的PWM脉冲相位可表示为

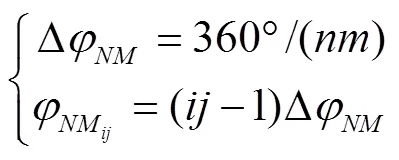
先按“站内”错相相同方法把各节点控制器下电磁阀都分为8组，PWM周期同取10 s，可知各电磁阀组的相位需错开9°，即0.25 s。

2.2.2 错相结果

在所建立的整机水力模型上，依次实施上述3种PWM脉冲错相方式，得到各错相方式下的喷灌机进水口压力曲线和流量曲线，如图9所示。

图9 不同错相方式下的喷灌机进水口压力和流量

从图9a知，3种错相方式分别将最大压力脉动幅度从错相前的0.60 MPa减小到了0.09、0.05、0.01 MPa，可见3种错相方式均可大幅减小变量喷灌过程中的压力脉动幅度，其中“站间+站内”错相方式下的压力脉动幅度最小，减幅效果最明显，但压力脉动频率最大；而“站间”错相方式对应的压力脉动幅度虽相对稍大，但脉动频率最小。对于选用何种错相方式，应结合喷灌机实体系统的机械振动固有频率等因素来考虑。

从图9b可知，使用3种错相方式后，变量喷灌机整机所需最大喷灌流量均远低于错相前。其中，使用“站间+站内”错相方式时，变量喷灌机所需最大喷灌流量最低。由此可知，PWM脉冲相位错开方法可有效提高泵站利用率，进而降低系统构建成本。

另外，当分别采用3种错相方式时，统计在单个PWM周期内各时刻的瞬间开阀个数和瞬间关阀个数，结果如图10。从图可知，错相前由于瞬间开阀（或关阀）的数量多达75个，导致主输水管道流量阶跃幅度较大，从而产生较大幅度的压力脉动，而使用3种错相方式均可减小瞬间开阀（或关阀）的数量，其中“站间”错相时最多16个，“站内”错相时最多10个，“站间+站内”错相时最多只有2个，进而对应了逐渐减小的主输水管道流量阶跃幅度以及逐渐减小的压力脉动幅度。

图10 单个PWM周期内各时刻瞬间开阀和关阀数

最后，在研制的大型PWM变量喷灌机实体系统上实现3种错相方式后，PWM周期同取10 s、PWM占空比同取50%、变量喷灌机保持静止，开展田间变量喷洒试验，试验时通过安装在变量喷灌机进水口处的压力传感器进行压力采集，并将采集数据进行中值滤波处理后得到不同条件下的喷灌机进水口压力曲线，如图11。

对比图8中的喷灌机进水口压力曲线与0.20 MPa泵站目标压力值下、2#节点控制器采用“站内”错相方式进行变量喷灌（其他喷头PWM占空比设为100%）时的喷灌机进水口压力曲线，可看出喷灌机进水口最大压力脉动幅度从错相前的0.07 MPa减小到了“站内”错相时的0.025 MPa。从而证明了“站内”错相方式的有效性。

从0.15和0.20 MPa两个泵站目标压力值下、整机采用“站间+站内”错相时的喷灌机进水口压力曲线可以看出，在整机进行变量喷灌时，变量喷灌机压力脉动的幅度值仍然较小，且随系统作业压力的增大而变化不大。再次说明了所提PWM脉冲错相方法可有效缓减变量喷灌过程中的压力脉动。

图11 PWM脉冲错相后的喷灌机进水口压力试验结果

此外，考虑到相位错开对变量喷灌机的喷洒均匀性和变量灌溉控制误差产生影响的可能性，喷灌机整机采用“站内+站间”错相方式，泵站目标压力取0.20 MPa，在地形平坦处，按照国标GB/T 19797-2012[23]中相关要求开展田间喷灌试验，如图12。分别设置平移喷灌速度0.75 m/min，旋转喷灌0.007 5 rad/min，获取了变量喷灌机在不同占空比下的喷洒均匀性和变量灌溉控制误差（分别按平移喷灌时的克里斯琴森水量分布均匀系数计算公式、旋转喷灌时的赫尔曼-海因水量分布均匀系数计算公式和变量灌溉控制误差计算公式进行计算[22,24-25]），试验结果如表2，可以看出，此时变量喷灌机在2种喷灌模式下的喷洒均匀性均大于85%，变量灌溉控制误差均小于5%。说明在采用PWM脉冲相位错开方法时，变量喷灌机仍具有较好的喷洒均匀性和变量灌溉控制误差。

图12 喷洒均匀性和变量灌溉控制误差测量试验现场

表2 喷洒均匀性和变量灌溉控制误差

3 结 论

针对大型PWM变量喷灌机在变量喷灌过程中的脉动激振问题，基于Matlab/Simulink，对研制的大型PWM变量喷灌机实体系统的水力模型进行了构建，并对变量喷灌过程中的压力脉动进行了分析、改善和验证。结果表明：

1）单一喷头的实际出水量在变量区虽然与PWM占空比有较好的线性关系，但均与理论值之间存在一定偏差，该偏差值与电磁阀的开关特性有关。另外，喷灌机整机最大压降发生在主塔车处（约0.037 MPa），单跨压力损失沿水流前进方向逐渐减小。

2）变量喷灌过程中，在电磁阀快速打开和关闭瞬间，因主输水管道内存在流量突变，故会产生压力脉动。压力脉动幅度与占空比大小无关，而与系统作业压力水平、同时开阀或关阀数、及供水系统压力调节响应时间正相关。

3）将控制电磁阀开闭的各路PWM脉冲相位进行错开是减小变量喷灌时压力脉动幅度和提高泵站利用率的有效方法。该方法从具体实施上可分为“站间”错相、“站内”错相和“站间+站内”错相，三者相比而言，“站间+站内”错相方式对压力脉动的减幅效果最明显，可将最大压力脉动幅度从错相前的0.60 MPa减小到0.01 MPa，但压力脉动频率稍大，而当采用“站间”错相方式时，压力脉动频率最小，但减幅效果相比略差，选用时应结合实际需求和变量喷灌机本身的机械振动固有频率等因素考虑。此外，在采用PWM脉冲相位错开方法时，变量喷灌机在平移和旋转2种喷灌模式下的喷洒均匀性均大于85%，变量灌溉控制误差均小于5%。

[1] Evans R G, Han S, Schneider S M, et al. Precision center pivot irrigation for efficient use of water and nitrogen [C]//Proceedings of the 3rd International Conference on Precision Agriculture,1996: 75-84.

[2] LaRue J L. Variable rate irrigation 2010 field results [C]//American Society of Agricultural and Biological Engineers,2011: Paper No.1110787.

[3] 韩文霆，吴普特，冯浩，等. 方形喷洒域变量施水精确灌溉喷头实现理论研究[J]. 干旱地区农业研究，2003，21(2)：105-107.

Han Wenting, Wu Pute, Feng Hao, et al. Variable-rate sprinklers for precision irrigation on square area[J]. Agricultural Research in the Arid Areas, 2003, 21(2): 105-107. (in Chinese with English abstract)

[4] Yang Qing, Pang Shujie, Yang Chenghai, et al. Variable rate irrigation control system integrated with GPS and GIS[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of CSAE), 2006, 22(10): 134-138.

杨青，庞树杰，杨成海，等. 集成GPS和GIS技术的变量灌溉控制系统[J]. 农业工程学报，2006，22(10)：134-138.(in English with Chinese abstract)

[5] 胡振方. 基于热红外成像技术的自走式实时变量灌溉机的设计与试验研究[D]. 北京：中国农业大学，2014.

Hu Zhenfang. Research and Eperiment of Self-propelled Variable Irrigation System Based on Infrared Thermography[D]. Beijing:China Agricultural University, 2014.(in Chinese with English abstract)

[6] Robert G E, Jake L R, Kenneth C S, et al. Adoption of site-specific variable rate sprinkler irrigation systems[J]. Irrigation Science,2013, 31(4): 871-887.

[7] Michael D D, Calvin P. Uniformity testing of variable-rate center pivot irrigation control systems[J]. Precision Agriculture, 2006, 7(3): 205-218.

[8] 黄小林，李文涛，周志宇，等. 平移式变量喷灌机整机有风喷灌水深分布求取与修正[J]. 机械设计与研究，2019，35(5)：141-145.

Huang Xiaolin, Li Wentao, Zhou Zhiyu, et al. Calculation and correction on application depth distribution of the whole lateral move variable rate irrigation system in windy condition[J]. Mechanical Design and Research, 2019, 35(5): 141-145.(in Chinese with English abstract)

[9] 赵伟霞，李久生，栗岩峰. 大型喷灌机变量灌溉技术研究进展[J]. 农业工程学报，2016，32(13)：1-7.

Zhao Weixia, Li Jiusheng, Li Yanfeng. Review on variable rate irrigation with continuously moving sprinkler machines[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of CSAE), 2016, 32(13): 1-7.(in Chinese with English abstract)

[10] 陶帅，李文涛，黄小林，等. 大型喷灌机喷头PWM变量脉冲的实现[J]. 农机化研究，2021，43(5)：18-22.

Tao Shuai, Li Wentao, Huang Xiaolin, et al. The realization of PWM variable pulse for the sprinkler of large-scale irrigation machine[J]. Journal of Agricultural Mechanization Research, 2021, 43(5): 18-22. (in Chinese with English abstract)

[11] 刘忠潮. 计算喷灌管道沿程水头损失的多口系数问题[J].节水灌溉，1982(2)：44-46.

[12] Edmar J, Scalopi. Adjusted F factor for multiple-outlet pipes[J]. Journal of Irrigation and Drainage Engineering, 1988, 114(1): 169.

[13] 朱广军. 大跨距平移喷灌机结构稳定性与灌水均匀性分析[D]. 合肥：安徽农业大学，2016.

Zhu Guangjun. The Structural Stability and Irrigation Uniformity Analysis of Large-span Translatison Prinkler Machine[D]. Hefei: Anhui Agricultural University, 2016.(in Chinese with English abstract)

[14] 魏永曜. 多支点喷灌系统管道的水力计算[J]. 节水灌溉，1982(4)：13-20.

[15] Kincaid D C, Heermann D F. Pressure distribution on a center-pivot sprinkler irrigation system[J]. Amer Soc Agr Eng Trans Asae, 1970(5): 556-558.

[16] 张云龙，严海军，王建东. 圆形喷灌机系统两井泵汇流装置水力性能研究[J]. 灌溉排水学报，2019，38(4)：48-54.

Zhang Yunlong, Yan Haijun, Wang Jiandong. Hydraulic characteristics at the confluence of two submersible pumps in center-pivot Irrigation[J]. Journal of Irrigation and Drainage, 2019, 38(4): 48-54.(in Chinese with English abstract)

[17] 张琛. 灌溉系统直动式压力调节器动力学模型与性能优化研究[D]. 北京：中国农业大学，2016.

Zhang Chen. Dynamic Model and Optimization of Regulating Performance of Direct-acting Pressure Regulator for Irrigation System[D]. Beijing: China Agricultural University, 2016. (in Chinese with English abstract)

[18] 姚磊. 基于Simulink的流体管网仿真[J].控制与信息技术，2010(5)：5-8，22.

Yao Lei. Simulation of fluid pipe net based on simulink[J]. Control and Information Technology, 2010(5): 5-8, 22.(in Chinese with English abstract)

[19] 田树军，张宏. 液压管路动态特性的Simulink仿真研究[J].系统仿真学报，2006，18(5)：1136-1138，1146.

Tian Shujun, Zhang Hong. Study on simulation of hydraulic pipelines’dynamic characteristic by simulink software[J]. Journal of System Simulation, 2006, 18(5): 1136-1138, 1146.(in Chinese with English abstract)

[20] 洪明，李援农，马英杰，等. 低压条件下滴灌毛管水头损失试验研究[J]. 灌溉排水学报，2010，29(1)：50-52，73.

Hong Ming, Li Yuannong, Ma Yingjie, et al. Head loss experimental analysis of trickle irrigation under the low pressure[J]. Journal of Irrigation and Drainage, 2010, 29(1): 50-52, 73.(in Chinese with English abstract)

[21] 周志宇，陶帅，莫锦秋. 圆形PWM变量喷灌机喷灌特性的仿真研究[J]. 农机化研究，2020，42(5)：15-24.

Zhou Zhiyu, Tao Shuai, Mo Jinqiu. Simulation research on irrigation features of PWM center pivot sprinkler irrigation system[J]. Journal of Agricultural Mechanization Research, 2020, 42(5): 15-24.(in Chinese with English abstract)

[22] 王勇. 供水系统水锤数值计算及动态模拟[D]. 合肥：合肥工业大学，2009.

Wang Yong. Numerical Calculation and Dynamic Simulation of Water Hammer in Water Supply System[D]. Hefei: Hefei University of Technology, 2019.(in Chinese with English abstract)

[23] GB/T 19797-2012，农业灌溉设备中心支轴式和平移式喷灌机水量分布均匀度的测定[S].

[24] ASABE Standards. S436.1, Test procedure for determining the uniformity of water distribution of center pivot and lateral move irrigation machines equipped with spray or sprinkler nozzles[S]. St Joseph, Mich: ASABE, 2007.

[25] 莫锦秋，周志宇，陶帅，等. 基于PWM技术的平移式变量喷灌机喷头流量分配方法[J]. 农业机械学报，2018，49(10)：163-171.

Mo Jinqiu, Zhou Zhiyu, Tao Shuai, et al.Sprinkler flow rate distribution method in lateral moving variable rate irrigation system based on PWM[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(10): 163-171. (in Chinese with English abstract)

Research and optimization of hydraulic characteristics of large-scale variable sprinkler irrigation machine based on PWM technology

Mo Jinqiu, Huang Xiaolin, Li Wentao, Li Yanming

(,,200240,)

Although the variable sprinkler irrigation machine based on pulse width modulation (PWM) technology can achieve more sophisticated water management in plots, the continuous opening and closing actions of the solenoid valve that realise variable rate irrigation make the flow rate of the main pipeline of the variable sprinkler irrigation machine a continuous and stepped change, which in turn leads to pressure pulsation and mechanical excitation in the variable sprinkler irrigation process. Based on Matlab/Simulink, the pressure pulsation of the large-scale variable sprinkler irrigation machine based on PWM technology in the variable sprinkler irrigation process was analyzed and improved. Regarding the developed large-scale variable sprinkler irrigation machine based on PWM technology, the hydraulic model of the key components and the whole machine were constructed first, and the correctness of the models were verified by experiments. Then based on the built hydraulic models of the whole machine, the pressure pulsation of the variable sprinkler machine was analyzed, and the law of the pressure pulsation in the variable sprinkler irrigation process was obtained. The results indicated that the amplitude of pressure pulsation had no effects on the duty cycle of the PWM pulse while was positively related to the operating pressure level of the system, the number of valves opened or closed at the same time, and the response time of the pressure adjustment of the water supply system. Furthermore, in order to reduce the number of valves that are opened or closed at the same time, the mitigation method of PWM pulse phase staggering was proposed, and three specific implementations of the method had been introduced, including staggering phase between stations, staggering phase in the station, and staggering phase between stations and within the station. Finally, the simulation analysis of the whole machine with implementing the PWM pulse phase staggering method on the model proved that three proposed staggering methods could significantly reduce the pressure pulsation amplitude in the variable sprinkler irrigation process, and also effectively improve the utilization rate of the pumping station. In particularly, the method that staggering phase between stations and within the station had the most obvious effectiveness on reducing pressure pulsation, which can reduce the maximum pressure pulsation amplitude from 0.60 MPa before phase staggering to 0.01 MPa. In addition, field experiments after realizing the PWM pulse phase staggering method on the developed large-scale variable sprinkler irrigation machine based on PWM technology further verify the effectiveness of the proposed PWM pulse phase staggering method in reducing pressure pulsation and mechanical excitation. The results in field experiment showed that the variable sprinkler irrigation machine still has good spray uniformity and variable irrigation control error when using the PWM phase staggering method. These research results can not only provide relatively stable pressure conditions for variable rate irrigation based on PWM technology to ensure the control accuracy in the variable sprinkler irrigation process, but also reduce the mechanical excitation caused by pressure pulsation to ensure the safety of the equipment.

models; pressure pulsation; large-scale sprinkler irrigation machine; variable rate irrigation; pulse width modulation

莫锦秋，黄小林，李文涛，等. 基于PWM技术的大型变量喷灌机整机水力性能研究及优化[J]. 农业工程学报，2020，36(19)：76-85.doi：10.11975/j.issn.1002-6819.2020.19.009 http://www.tcsae.org

Mo Jinqiu, Huang Xiaolin, Li Wentao, et al. Research and optimization of hydraulic characteristics of large-scale variable sprinkler irrigation machine based on PWM technology[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(19): 76-85. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.19.009 http://www.tcsae.org

2020-07-19

2020-09-20

国家重点研发计划项目(2017YFD0700504-2)

莫锦秋，博士，副教授，主要从事机电系统集成控制研究。Email：mojinqiu@sjtu.edu.cn

10.11975/j.issn.1002-6819.2020.19.009

S277.94

A

1002-6819(2020)-19-0076-10