大容量外转子永磁风力发电机组转子结构的轻量化设计*

张 坤，于慎波*，翟凤晨，卢华兴，刘 伟

(1.沈阳工业大学 机械工程学院，辽宁 沈阳 110870；2.国家电投集团 科学技术研究院有限公司，北京 100029)

0 引 言

随着风力发电机组装机容量的急剧增加，发电机组的体积和质量也随之上升，带来发电机组在制造、加工、运输、安装上的困难，电机的轻量化设计成为有待解决的难题。

针对电机轻量化问题，国内外研究人员进行了大量探索。文献[1，2]通过对电机轭部磁路分析，优化了轭部设计，提高了电机的转矩密度，达到了电机减重目的。文献[3，4]电机设计采用超导技术，转子磁极使用超导磁体，定子线圈采用MgB2超导绕组，采用超导技术可实现无轭部定子设计，提高了电机功率密度，减少了电枢损耗，减轻了电机重量。

以上电机减重方法之出发点为优化电机电磁性能，通过较少绕组来减小磁极重量，并未从机械角度去考虑电机减重。文献[5，6]利用激光增材先进制造技术，将粉末粘结剂喷射在由晶格结构设计的兆瓦级发电机表面，以减轻重量且能保证强度；晶格结构能大大减轻结构重量，但激光增材会增加转子制造难度，提高转子的制造成本。文献[7]为7 MW风力发电机定子设计了一种新型的抗定子变形结构，提高了机座在径向方向上的抗拉强度，减小了机座在径向方向上的变形。

在满足大容量外转子永磁发电机转子设计要求基础上[8]，笔者综合考虑风力发电机工况特性以及电磁力情况，使用拓扑优化、多目标灵敏度分析、响应面优化相结合的方法，探索风力发电机转子的快速轻量化设计。

1 发电机设计参数

风力发电机组设计参数如表1所示。

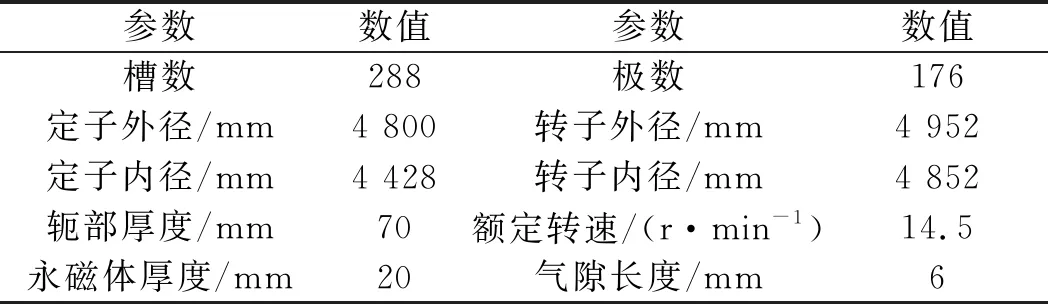
表1 风力发电机组设计参数

2 外转子结构有限元分析

风力发电机转子运行中除受自身重力外,还承受叶片通过轮毂传递的力、转矩、风力发电机内部电磁力(计算得出径向电磁力幅值161 226 N/m2)。叶片通过轮毂作用到转子的力，沿定子轴传递到塔架，对转子作用较小，故设计中只考虑轮毂传递转矩对转子的作用。风力发电机外转子主要依靠轴承支承，转子约束面为内侧法兰盘面。

笔者对转子结构进行有限元分析，得到了转子的变形、应力图，如图1所示。

图1 变形、应力图

不同载荷分析汇总如表2所示。

表2 不同载荷分析汇总

由图1可得：(1)转子最大变形为转子最顶端位置，变形方向为Z轴负半轴，主要因为自身重力和电磁力同向作用；(2)极限载荷最大变形量为1.287 9 mm，占气隙长度的21.5%。

因此，转子结构必须进行优化设计。转子前端盖与外圈变形较小，笔者设定二者为优化区域。

3 拓扑优化

结构的拓扑优化技术可以在给定载荷及约束条件下，寻找到使结构设计目标最优化的材料密度分布，使所设计结构利用材料率更高、受力分布更合理[9]。

拓扑优化最终决定了每个设计单元中材料的存在，以设计变量的二进制(0-1或空隙-实体)形式呈现。大规模离散问题不允许使用数值方法求解，因此通过引入插值方案，将离散问题简化为连续问题[10]。

笔者以风力发电机转子结构为优化对象，采用变密度法，以变形能最小化为目标，限制体积分数为约束条件进行拓扑优化，即：

(1)

式中：u—位移矢量；b—体力；t—力矢量；σ(u)—依据位移矢量的应力矢量；δu—虚拟位移矢量；u0—允许动力学运动空间；ρ—常规密度场，作为设计变量；ρmin—密度下限。

使用变密度法(SIMP)模型的插值方案，避免离散求解问题。SIMP法以幂指数形式表达方程：

(2)

式中：Em—第m个单元弹性模量；E0—实体单元弹性模量；p—惩罚因子；xn—相对密度。

当xn=1，即当前单元相对密度为1，表示该单元被填满材料，可承受载荷；xn=0表示单元相对密度为0，该单元无材料填充，无法承受载荷。SIMP法模型中加入的惩罚系数p，可以对介于中间密度的材料进行惩罚。能够使材料单元密度值更加快速地向“0”或“1”聚集[11，12]，使计算模型更好地趋近离散变量的拓扑优化模型。

为方便载荷的施加，拓扑优化中使用Rbe3单元，约束为转子法兰盘的6个自由度，得到最佳拓扑优化方案，优化中添加拔模约束、棋盘格参数、周向循环对称约束；体积分数为分析约束条件。

前端盖经过36次拓扑优化迭代计算，转子筒经过37拓扑优化迭代计算，得到拓扑优化计算结果，如图2所示。

图2 拓扑优化结果

图2中，深色单元表示单元密度较高，承受载荷，需要保留材料；亮色单元表示单元密度较低，可以减少或去除材料[13]。

取体积分数0.3的优化结果，得到的材料分布图如图3所示。

图3 体积分数0.3材料分布图

通过拓扑优化，能清楚地了解结构中的优化区域，更有目的性地进行多目标灵敏度、以及尺寸优化分析[14，15]；根据材料分布，确定转子优化区域，明确优化方案。

4 发电机转子结构优化

4.1 尺寸参数确定

根据拓扑优化结果，又由于发电机运行在海上，笔者采用密闭设计，且不能完全按照拓扑优化结果将材料全部去除。参考材料分布图，前端盖圆盘优化方案为减少原始设计厚度，内侧添加加强筋。在分析模型中笔者保持原端盖厚度，采用切除材料方案，能更好地对端盖结构进行优化，端盖内侧未去除材料即为加强筋；转子外筒重新设计永磁体内嵌式结构。

参数化建模如图4所示。

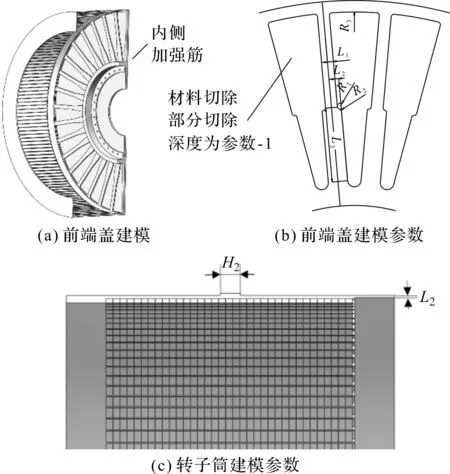
图4 参数化建模

4.2 灵敏度分析

灵敏度分析是通过数学的方法对输入及输出参数的关系进行分析，然后依据计算得到的各个参数之间的变化规律，确定对结构影响较大的参数为优化参数[16]。笔者使用有限差分法获得灵敏度参数。中心差分法公式为：

(3)

式中：xj+=(x1,x2,…,xj-1,xj-1+Δxj,xj+1,…xm)；xj-=(x1,x2,…,xj-1,xj-1-Δxj,xj+1,…xm)；Δxj—设计变量的微小摄动量；y—目标响应。

笔者将尺寸参数输入，通过计算得到输入参数对变形、应力、质量的灵敏度，如图5所示。

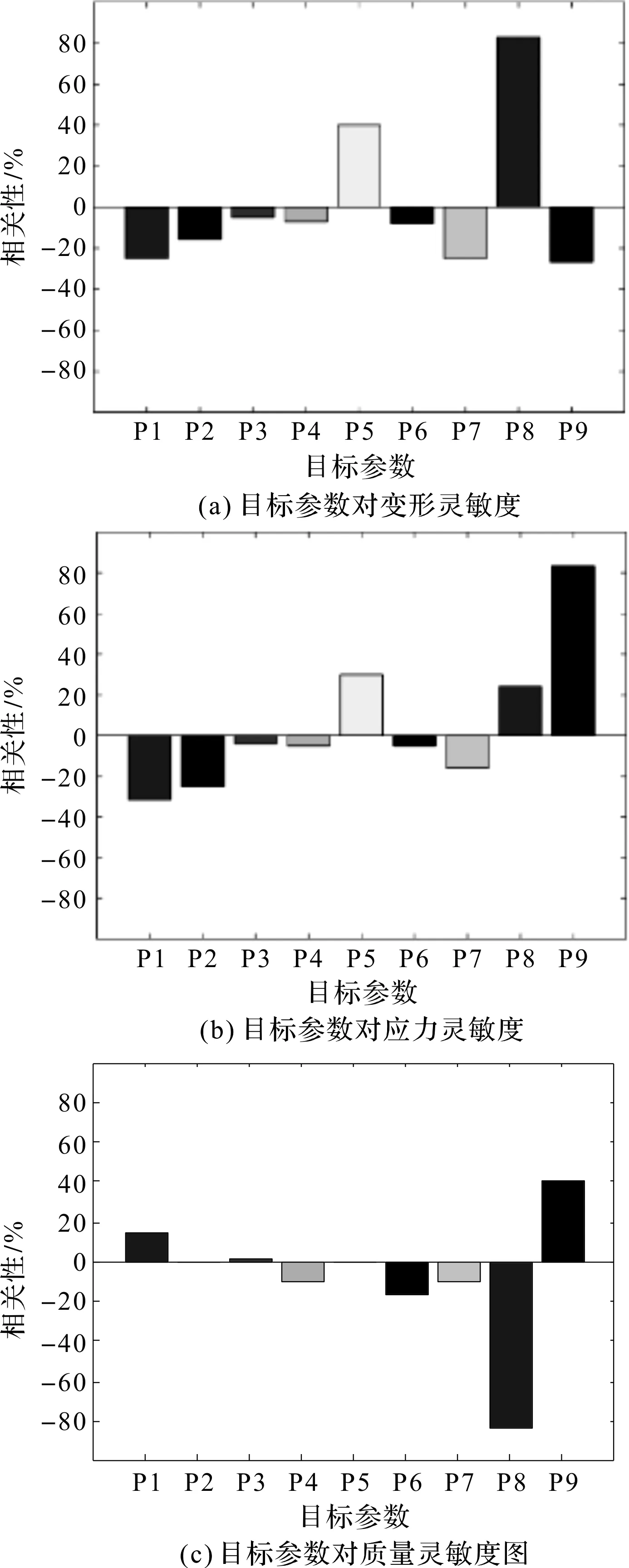
图5 灵敏度图

由图5可知，目标参数对风力发电机转子结构影响存在差别，其中，P1、P2、P5、P8、P9对形变影响较大，P8影响最大，即转子外端盖切除材料越多，变形越大；对应力影响程度较大的参数为P1、P2、P5、P8、P9，对质量影响最大的参数为P8，即H1参数越大转子质量越小，符合实际情况。

根据输入参数对目标参数的灵敏度值的大小，笔者筛选出对目标参数影响大的参数P1、P2、P6、P8、P9，对参数建模中标注的L1，L2，R3、H1、H2尺寸进行响应面尺寸优化。

4.3 响应面模型建立

在多目标优化中，目标之间相互冲突，很难找到所有目标均为最优的最优解，而是存在一系列有效解。响应面法是结合数学计算与统计算法[17]，生成不用实验参数组合构成响应面模型，最后通过优化算法得出全局最优解。响应面优化方法采用拉丁超立方试验方法，才提高分析效率[18]。

响应面优化通常采用二阶数学模型，对于e个变量，二次多项式响应模型为：

(4)

式中：x—设计变量，x=(x1,x2,…,xe)；a0，ai，aii，aij—待定系数。

(5)

式中：X—基函数矩阵；G—e个点得出的响应。

笔者通过拉丁超立方方法得出5个参数的100组试验点，通过标准二次回归方程拟合参数与优化目标之间的关系，构建出响应面模型。

输入参数对变形、质量的响应面图如图6所示。

图6 输入参数对变形、质量的响应面图

4.4 优化结果

笔者将变形、应力、质量作为目标参数，变形、应力约束限制为最小，质量约束限制为小于等于12 000 kg，并根据灵敏度分析得出目标参数设定取值范围，如表3所示。

表3 设计参数取值范围

笔者将转子质量作为第一参考量，变形作为第二参考量。经响应面优化算法对输入参数、目标参数分析，得到3组最优解，优化方案结果如表4所示。

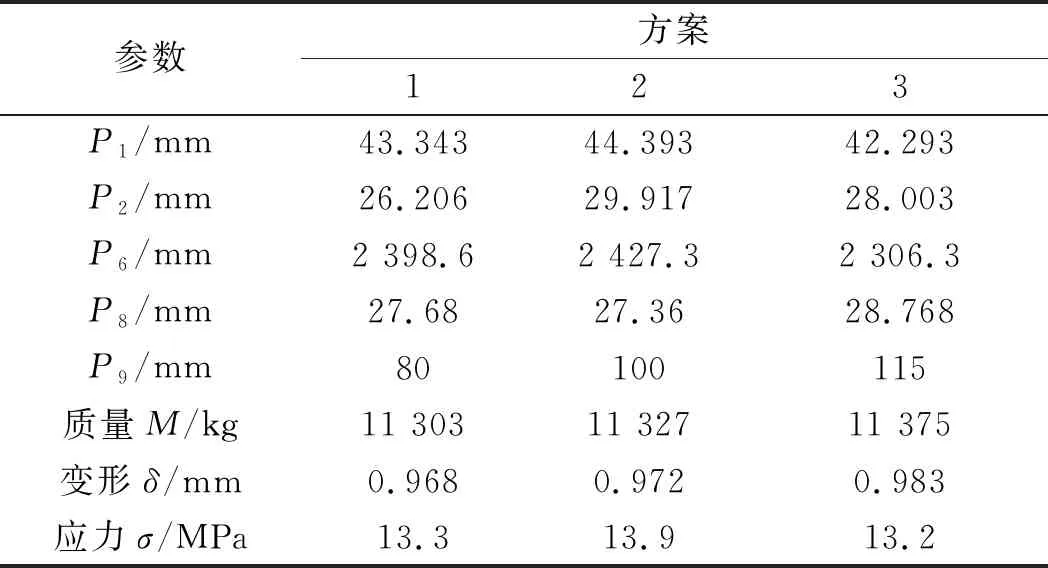
表4 优化方案结果

表4中3组方案对比，方案1质量最小，变形也最小。故笔者选择第1方案为优化设计方案。

笔者提取方案1的优化参数，将优化参数进行修正，得到最终设计尺寸，优化参数修正前后对比如表5所示。

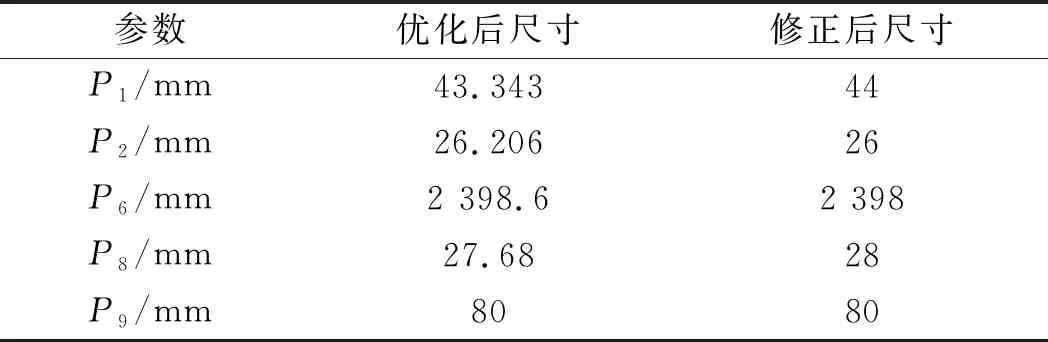
表5 优化参数修正前后对比

表5中的修正参数作为最终设计尺寸。

笔者选择变形最大组极限载荷进行有限元分析，得到新设计结构计算结果，与初始设计结构计算结果进行对比，转子优化前后参数对比如表6所示。

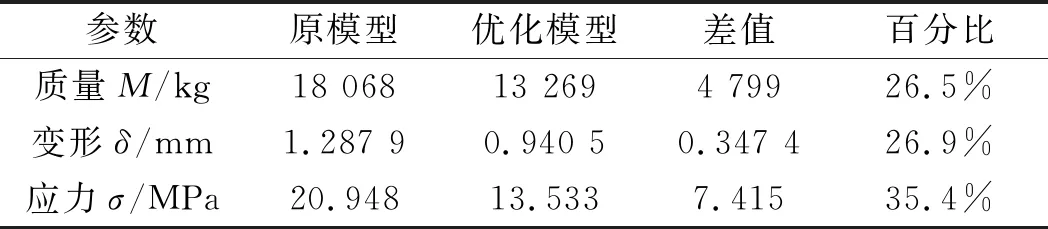
表6 转子优化前后参数对比

由表6可知，转子优化前后，质量减小4 799 kg，减少26.5%；变形减少0.347 4 mm，减少26.9%；且应力集中减弱，符合风力发电机轻量化设计要求。

5 结束语

针对大容量永磁风力发电机组外转子结构重量较大、增加机组负荷、影响机组安全性的问题，笔者进行了转子轻量化设计，得到结论如下:

(1)永磁体嵌入转子内壁凹槽内，永磁体对转子起到支撑作用，不但可使转子壁变薄，而且变形量减少，其重量减轻了2 065 kg；

(2)转子前端盖变薄，转子内侧增加了加强筋，保证了转子结构刚度，该项措施使重量减少了2 734 kg。加强筋可起到风扇的作用，有助于端部绕组均热。