为什么点那么难“描”

阮萍扬

(福建省泉州师范学院附属中学 福建 泉州 362000)

建系法是解决高中理科立体几何问题的一种有效方法，模式化也比较明显，在完成建系和描点后，套入公式一般都可以解决问题，这类问题有较为明显的“套路解法”，照理学生的得分率要很高，但实践过程中笔者却发现情况截然相反。究其原因，其中一个主要的问题是学生不会描点，为什么点那么难描？可能是一些描点的“技巧”没有掌握好。

1.选择合适的空间直角坐标系

例题1:如图1，在四棱锥P-ABCD中，底面ABCD是边长为1的菱形，∠BAD=45°,PD=2,若平面PDC⊥底面ABCD，且PD⊥DC，求平面PAD与平面PBC所成锐二面角的余弦值。

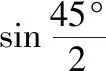
2.从空间向量角度进行描点

例题2:(2014课标1)如图5，三棱柱ABC-A1B1C1中，侧面BB1C1C为菱形，AB⊥B1C。(1)证明：AC=AB1；(2)若AC⊥AB1,∠CBB1=60°,AB=BC,求二面角A-A1B1-C1的余弦值。

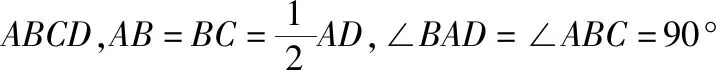
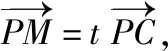
3.题目中核心信息遗漏

例题4:(2018课标1)如图9，四边形ABCD为正方形，E,F分别为AD,BC的中点，以DF为折痕把△DFC折起，使点C到达点P的位置，且PF⊥BF。(1)证明：平面PEF⊥平面ABFD；(2)求DP与平面ABFD所成角的正弦值。

解析:过点P做EF的垂线，交EF于点O,即PO⊥面ABCD。如图10建立空间直角坐标系，设AB=2，瞬间发现，所有的坐标都很难求。这是因为有一个核心信息遗漏了！遗漏了什么信息呢？遗漏了PF⊥面PED，就有PF⊥PE！这里△EPF是直角三角形！有了这个信息，那么描点就非常容易了！这样的命题手法非常高明，对学生来说是一个挑战，如果没有对信息进行再挖掘，仅仅通过表象信息去解决问题，往往无功而返耗时耗力。这给了我们一个提示，描点遇到障碍时，认真细读题目给出的信息，对信息进行二次挖掘，把隐藏的结论揭示出来，问题便迎刃而解。

总结

建系、描点、套公式，这是立体几何建系法的三步骤。描点成为最关键的一步。除了传统的将点投影到坐标平面或投影到坐标轴外，其实，我们还有一些“小技巧”、“补充结论”和“解题经验”来帮助建系和描点。